迭代阈值分割算法在电成像测井中的应用

齐瑞燕，吴进波，石 磊

（1.长江大学 地球物理与石油资源学院，湖北武汉 430100；2.中海石油（中国）有限公司湛江分公司，广东湛江 524000；3.中海石油深海开发有限公司，广东深圳 518000）

现存的关于图像分割的方法数目繁多，包括阈值分割法、区域分割法以及基于小波变换等特定理论的分割方法[1-3]，其中阈值分割法具有自身特有的优点，即简单实用且可以自适应获取最佳阈值，因此常被用在图像信息识别处理中。而阈值分割法最关键、最重要的一步就是确定图像的阈值，图像的阈值可以指定为单阈值也可以指定为多阈值，阈值确定方法可以通过人工指定，但其效率太低；可以通过最大类间方差法（Otsu）确定，此方法适合于双峰情况自动求取阈值，近几年也有许多学者基于Otsu 方法进行改造研究；另外，也可以通过迭代法来确定分割阈值[2-4]。

文中首先介绍了最小均方误差法和直方图法的阈值分割原理，以及阈值确定的3 种方法，然后采用迭代阈值分割算法，根据电成像测井图中裂缝、骨架、孔隙等不同部分灰度值存在差异的原理，通过迭代法指定了两个初始阈值，经过迭代计算后，最终确定了最佳分割阈值，进而对电成像测井图中不同的成分进行识别及提取。

1 阈值分割原理

阈值分割的原理，通常来说，就是设定一个阈值T或者两个阈值T1、T2，甚至是多个阈值T1、T2、T3等，将一幅图像像素的灰度直方图分成两个类或者3 个类，甚至是多个类[5]。这时，当该图像中某些像素的灰度值大小在同一个类范围内时，就认为这些像素属于图像中同一个物体；当该图像中另一些像素的灰度值大小在另一个类范围内时，就认为这些像素属于图像中另一个物体。故在图像分割过程中，如果能够实现对数据量的压缩进而简化图像分析处理的步骤，就会节省大量时间，而这正是阈值分割法具有的最大特点。

基于图像灰度直方图的阈值分割，是最简单、最容易理解的一种分割，它的原理是将一幅图像分为两个类，因此只需要确定一个分割阈值，这个分割阈值就是直方图中所有取值范围内的最小灰度值，也即两个峰值之间的谷底[3]。假设一幅图像f()x,y的背景区域和目标区域的灰度值分布都是比较均匀的，此时可选择图像中两个峰值之间的最小值作为分割阈值[3]。分割后的图像可定义为：

由基本数学知识可知，得到的g(x,y)公式是一个二值函数的表达式，它是函数f(x,y)经过阈值运算后得到的，得到的结果只有0 和1 两个数值，也就是把图像中各个不同的像素归为了两类，然后可根据需要自行将这两类像素分别用其他颜色填充，即可将图像中不同的物体分割开来。

过程如下：

1）将彩色图灰度化；

2）确定直方图，根据直方图选取阈值；

3）根据阈值进行图像分割；

4）将不同像素物体用不同的颜色填充。

最小均方误差法是利用一个分割阈值T将图像中物体的像素值分为两个类。通常分割阈值T可以采用最小均方误差法求出，但其中一个问题是，此方法需要进行大量复杂的运算才能得到均方误差最小的参数，故文中采用基于直方图法的原理对图像进行阈值分割。

2 阈值确定方法

直方图双峰法[6]，也称为mode 法。当图像比较简单，其灰度直方图具有较为典型的双峰特性时，即图像中只有背景和目标两个对象[6]，且在灰度直方图上各自形成一个最大灰度值，并且这两个最大灰度值之间具有明显的最小灰度值（谷底点）时，此时可选取最小灰度值（谷底点）作为分割阈值T，运用分割阈值T即可将图像分割开。

最大类间方差法[7-10]，也称为大津法。此方法确定阈值的思想是根据图像的灰度直方图，分割阈值T是由目标对象和背景对象之间的类间方差最大来动态确定的，对于具有双峰情况的图像，此方法可以自动地求取分割阈值T[7-10]。实现方法具体为：假定一幅图像只包含一个目标物体和图像背景两个对象，其中目标物体的像素总个数与整幅图像的像素个数之比为t1，且目标物体的像素灰度平均值为a1；图像背景的像素总个数与该图像所有像素个数的比值为t2(其中t2+t1=1)，且图像背景的像素灰度平均值为a2，那么该图像所有像素灰度平均值为[10]：

类间方差定义为:

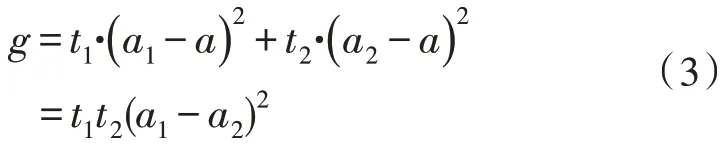
将灰度划分为1-N级，令T在[0,N-1]范围内变化，以步长1 依次增长取值，当T增长到某一个数值时，类间方差g能够取到所有取值中的最大值，这时T值便是此图像的最佳分割阈值。

迭代法的基本思想是观察整幅图像像素灰度值的分布情况，选取一个近似阈值作为初始阈值，一般情况选择整个图像的灰度均值作为初始阈值[11]，然后通过分割图像和修改阈值的迭代过程获得适合的最佳阈值，通过迭代法确定出最佳阈值，也即可以自适应地根据图像数据自动地选择阈值[11-14]。

迭代法阈值分割的步骤常分为五步。第一步：求初始阈值T，一般情况下初始阈值是通过图中所有像素值求得的平均值；第二步：用初始阈值T将图像中的像素值分成两个类，其中对应像素灰度值小于T的部分命名为G1，像素灰度值大于T的部分命名为G2。第三步：求取所有G1类中的像素平均值命名为m1，所有G2类中的像素平均值命名为m2。第四步:确定新的分割阈值Temp∶Temp=(m1+m2)/2。第五步：求新的分割阈值Temp与初始阈值之间的差值，并判断该差值是否小于预先设定的范围，如果是，就可对图像进行阈值分割；如果不是，则循环第一步到第四步，直到得到的差值小于预先设定的范围[15-18]。

3 实例分析

基于电成像测井图中相同成分之间颜色相差不大，不同成分之间颜色相差较大的原理，采用阈值分割法处理电成像测井图，将其分成3 部分，并把相同的成分用同一种颜色填充显示。实例分析部分使用两种方法确定阈值，并进行图像分割，一种方法是输出直方图，通过观察直方图进行人工设置阈值；另一种方法是使用迭代法进行阈值的确定，基于“一个阈值可以区分两种目标物，两个阈值可以区分3 个目标物，3 个阈值区分4 个目标物…”的原理，基于大量文献的阅读与所需程序的编写修改后，对于同一张图像的分割，设置了两个阈值，解决了如何将一幅图区分成3 部分，并进行填色显示的问题。先通过自己画的一幅简单几何图进行程序测试，测试成功后再对某地区A井的电成像测井图进行识别分割。

3.1 人工设置阈值

如图1 所示，共有4 张小图，按顺时针方向(即Matlab 处理顺序)分别是原图、灰度图、直方图以及阈值分割图。通过观察简单几何图对应的直方图，设置初始分割阈值分别为T1=100，T2=150。当图中某点的阈值小于T1时用黑色填充，也即长方形区域（目标区域1）；当图中某点的阈值大于T2时用白色填充，也即背景区域（目标区域2）；当图中某点的阈值介于T1=100 和T2=150 时用灰色填充，也即圆形区域（目标区域2）。仔细观察可以发现，大圆和小圆颜色相差不多，故可将3 个圆同时区分开来，并在最后的阈值分割图中将3 个圆用同一种颜色填充，长方形用同一种颜色填充，背景用另一种颜色填充，最后原图经阈值分割后得到的阈值分割图如图1(c)所示。

图1 简单几何图人工指定阈值处理过程

如图2 所示，对于某地区A 井电成像测井图，观察其对应的直方图后设置初始分割阈值分别为T1=66，T2=166，原理不变，即像素小于T1时用黑色填充，像素大于T2时用白色填充，介于T1和T2之间时用灰色填充，分割结果如图2(c)所示。

图2 某地区A井电成像测井图人工指定阈值处理过程

3.2 迭代法确定阈值

为了将测井资料电成像图分割为3 部分，在确定阈值时选取两个初始阈值，经过迭代法，最后确定最佳阈值。

利用迭代法求阈值的步骤如下：

1）分别取出最大灰度值Tmax和最小灰度值Tmin，再取其平均值T；

然后计算T值与最小灰度值Tmin的平均值作为T1，T值与最大灰度值Tmax的平均值作为T2；

3）当灰度值小于T1、灰度值介于T1和T2之间、灰度值大于T2时，分别确定这3 部分的灰度值及其总和，并分别计算其平均值。灰度值小于T1、介于T1和T2之间、大于T2时对应的灰度平均值分别为m1、m2、m3；

4）求出总的平均值Ttmp，也即新的阈值Ttmp：Ttmp=(m1+m2+m3)/3；

5）当T≠Ttmp时，令T=Ttmp，循环步骤2）到步骤4），直到当T＝Ttmp时，循环结束，分别给这3部分填色即可。

图3 为迭代阈值法图像分割的流程图。

图3 迭代阈值法图像分割流程图

图4 为简单几何迭代阈值法分割图，其初始阈值T1=110、T2=128，经过迭代运算后，得到的最佳分割阈值分别为T1=46、T2=100。

图4 简单几何迭代阈值法分割图

图5 为某地区A 井电成像测井图迭代阈值法分割图，其初始阈值T1=64、T2=128，经过迭代运算后，得到的最佳分割阈值分别为T1=44、T2=128。

图5 某地区A井电成像测井图迭代阈值法分割图

可以发现，简单几何图中的3 个圆没有被区分出来，而是被背景颜色淹没。电成像测井图的分割效果与人工设置阈值分割效果相似，结果较为理想。

从地质意义角度分析，根据电成像分析原理：地层电阻率越高，流经地层的电流越小，经过标准化处理后，图像上显示的像元的灰度越浅，例如致密的地层、骨架、石灰岩或砾石等；地层电阻率越低，流经地层的电流越大，经过标准化处理后，图像上显示的像元的灰度越深，例如泥岩、充满流体或泥质的裂缝、溶洞等。

由图2 或图5 某地区A 井电成像测井图可以看出，形似正弦曲线的黑色部分可能是含有流体或泥质的裂缝，白色部分可能是致密的地层或一部分为骨架，而灰色部分可能是普通的砂层。

4 结论

文中首先介绍了阈值分割原理及阈值确定方法，然后采用人工确定阈值和迭代法计算阈值两种阈值确定的方法，对简单几何图和电成像测井图进行图像分割处理，最后通过分析对比，得出结论：①对于比较简单的图像分割处理，可以采用双峰法求阈值的思想进行人工设置阈值；对于比较复杂的电成像图像分割处理，可以利用迭代法确定阈值进而对图像进行分割处理。②文中成功将图像分割为3 个目标区域，并用不同颜色进行填充。但仍然存在分割结果不是十分明显等缺点，还需进一步探索、研究。