2-UPR-PRU并联机构静刚度模型建立与性能分析

饶晨阳 徐灵敏 陈巧红

(1.浙江理工大学机械与自动控制学院， 杭州 310018； 2.浙江理工大学信息学院， 杭州 310018)

0 引言

相比于串联机构，并联机构具有精度高、载荷能力强、动态性能好等优点，作为骨架已广泛应用于各种先进制造装备中[1-3]。考虑末端执行器的输出特性，三自由度两转一移(Two rotations and one translation, 2R1T)并联机机构适用于复杂曲面加工的场合[2-7]。通过结合两个串联式移动导轨或在末端安装二自由度串联摆头，整机可实现五自由度运动，用于大型航空结构件加工打磨等[8-9]。

对用于高速高精度加工场合的2R1T并联机构，在设计阶段进行静刚度建模必不可少，既是机构静刚度性能分析的基础，同时也为实际样机设计和提高控制精度提供重要参考依据。静刚度建模主要研究在系统静力平衡的情况下，机构末端执行器的变形情况和外部载荷间的映射关系[10]。现有的并联机构刚度建模方法主要有[11-22]：有限元分析法[11-14]、矩阵结构分析法[15-18]和虚拟关节建模法[19-22]。有限元分析法通过借助有限元分析软件对模型进行网格划分，计算外部载荷作用下机构在某一位型下的变形情况，具有较高的精度。但由于机构在不同位型时需重新建模和划分网格，过程较为繁琐且耗时，不适用于参数优化。矩阵结构分析法则通过矩阵运算直接得到机构刚度矩阵，无需网格划分。但该方法涉及到高维矩阵运算，不适用于解析静刚度建模。虚拟关节建模法则通过考虑关节柔性，建立机构末端变形和外部载荷的关系，精度较高。但对于一些结构复杂的并联机构，该方法需进行大量的逆矩阵运算，计算效率不高。

基于并联机构刚度矩阵的特性，现已提出一些刚度指标用于性能评估及参数优化[11, 23-25]，如最大/最小特征值[24]、特征值平均数[11]、行列式[25]等。然而由于刚度矩阵中的元素量纲不统一，会导致基于刚度矩阵的指标物理意义不明确和解释错误[23]。

本文将对2-UPR-PRU三自由度2R1T并联机构[3-4]进行静刚度建模和性能评估。通过螺旋理论和应变能方法[26-28]得到各分支和整体刚度矩阵。借助ANSYS有限元软件，对2-UPR-PRU并联机构的理论变形结果和整体柔度矩阵进行数值仿真验证。利用虚功刚度指标(Virtual-work stiffness index, VSI)[28]评价2-UPR-PRU并联机构抵抗外部载荷的能力。通过改变2-UPR-PRU并联机构的操作高度分析讨论机构在姿态空间中的刚度性能分布图谱。

1 机构描述与位置逆解

1.1 机构描述

图1为2-UPR-PRU并联机构的三维模型，其中定平台和动平台由2条对称分布的UPR分支(B1A1/B2A2)和1条PRU分支(B3A3)连接，通过驱动3个P副可实现动平台的2个转动和1个移动。各分支中的关节转轴定义如下：2条UPR分支中U副的第1个转轴共线，且方向和PRU分支中U副的第1个转轴和固接在定平台上的R副转轴平行；2个UPR分支中U副的第2个转轴相互平行，且同时平行于和动平台固接的R副转轴和PRU分支中U副的第2个转轴。

如图1所示，2-UPR-PRU并联机构定/动坐标系定义为：定坐标系Oxyz的原点O为B1B2的中心点，x轴与B3O重合，y轴指向点B1，z轴根据右手定则垂直向下。动坐标系ouvw的原点o为A1A2的中心点，u轴沿着A3o方向，v轴沿着oA1方向，w轴垂直于动平台向下。2-UPR-PRU并联机构的杆件参数定义如下：oA1、oA2为l1，OB1、OB2为l2，oA3为l3，B3A3为l。

1.2 位置逆解

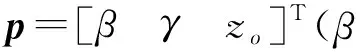
根据2-UPR-PRU并联机构的旋转特点[3-4]，动坐标系ouvw相对于定坐标系Oxyz的旋转矩阵ORo可表示为

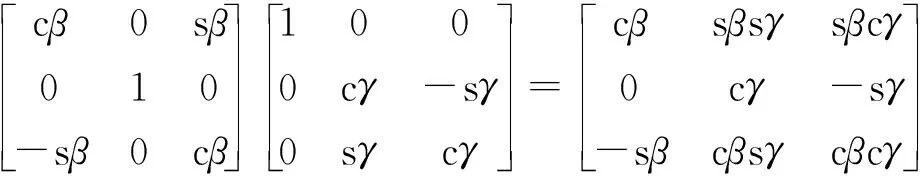
(1)

式中Ry,β、Ru,γ——绕y轴和u轴的旋转矩阵

s、c——正弦函数和余弦函数

由于2-UPR-PRU并联机构的结构特征，动平台末端点o的运动限制在y=0平面内，这一特点大大降低了机构反解推导的复杂性。如图1所示，ci表示BiAi(i=1,2,3)位置矢量。另外，机构中的oAi和OBi位置矢量可分别表示为

(2)

联立式(1)、(2)，代入到闭环矢量链ci=p+ai-bi中，可得到2-UPR-PRU并联机构的逆解表达式为

(3)

2 静刚度建模

结合螺旋理论和应变能方法，对2-UPR-PRU并联机构进行各分支和整机的静刚度建模分析，用于评估外部载荷对末端位姿输出的影响。在构建静刚度模型前，需进行如下假设：①本研究考虑杆件的柔性，包括弯曲、剪切、拉伸/压缩和扭转变形。②机构中的定平台、动平台和所有运动关节均被认为是刚体。③忽略机构中各部件的重力和摩擦力。

2.1 分支刚度矩阵

选用第1条UPR分支和PRU分支作为研究对象。在构建分支刚度矩阵前，需确定分支的驱动力螺旋和约束力螺旋[29]。参照文献[3]，在定坐标系下，第1条UPR分支的驱动/约束力螺旋可表示为

(4)

如图2a所示，驱动/约束力螺旋的幅值分别定义为f11、f12和m11。为方便进行投影，在UPR分支中建立分支坐标系A1x1y1z1，其中y1轴沿着R副的轴线方向，z1轴沿着B1A1方向，x1轴可通过右手定则得到，如图2b所示。根据力学知识，作用于点B1的约束力f12等效于作用于点A1的约束力f12加上沿着x1轴的约束力矩m12，其可表示为

m12=-q1z1×f12y1=q1f12x1=m12x1

(5)

根据图2b中驱动/约束力的投影结果，UPR分支中任意横截面处的内力/内力矩可表示为

(6)

式中n1——约束力矩m11的方向矢量

v1——选定横截面到点A1的距离

因此，UPR分支应变能可表示为

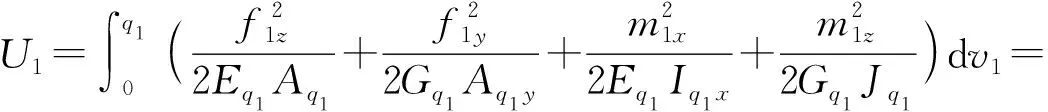
(7)

式中Eq1——UPR分支弹性模量

Gq1——UPR分支剪切模量

Aq1——分支横截面面积

Aq1y——分支横截面沿着y1轴的有效面积

Iq1x——关于x1轴的横截面惯性矩

Jq1——横截面极惯性矩

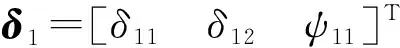
(8)

将式(8)表示为矩阵形式

(9)

其中

(10)

式中C1——3×3的对称分支柔度矩阵

因此，根据式(10)可得到第1条UPR分支的刚度矩阵K1为

(11)

PRU分支的刚度矩阵构建过程类似于UPR分支。在定坐标系下，该分支的驱动/约束力螺旋可表示为

(12)

PRU分支上的3个驱动/约束力如图3a所示，其幅值分别定义为f31、f32和m31。同样地，在PRU分支中建立分支坐标系A3x3y3z3，其中x3轴沿着R副的轴线方向，z3轴沿着B3A3方向，y3轴可通过右手定则得到，如图3b所示。PRU分支中任意横截面处的内力/内力矩可表示为

(13)

式中n3——约束力矩m31的方向矢量

v3——选定横截面到点A3的距离

(14)

其中

(15)

式中El——PRU分支弹性模量

Gl——PRU分支剪切模量

Al——分支横截面的面积

Alx——分支横截面沿着x3轴的有效面积

Ily——关于y3轴的横截面惯性矩

Jl——横截面极惯性矩

同理，PRU分支的刚度矩阵K3为

(16)

2.2 整体刚度矩阵

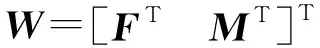
动平台的力/力矩平衡方程可表示为

(17)

其中

式中JW1——分支1中维度为6×3的力矩阵

JW2——分支2中维度为6×3的力矩阵

JW3——分支3中维度为6×3的力矩阵

JW——6×9的力矩阵

f1——分支1中3×1的力幅值矢量

f2——分支2中3×1的力幅值矢量

f3——分支3中3×1的力幅值矢量

f——9×1的力幅值矢量

根据虚功原理，各分支变形矢量和动平台原点的变形矢量D满足如下关系

(18)

式中 δx、δy、δz——机构沿着x轴、y轴和z轴的线性变形

δθ、δφ、δψ——机构绕着x轴、y轴和z轴的角度变形

结合式(17)、(18)，δi(i=1,2,3)和D的变形协调方程可表示为

(19)

将式(9)、(14)、(19)代入式(17)可得

(20)

从式(20)可得2-UPR-PRU并联机构的整体刚度矩阵为

(21)

通过式(19)～(21)得到机构中各分支的力幅值矢量表示为

(22)

2.3 理论刚度模型和有限元模型对比

在分析机构刚度性能前，需验证2-UPR-PRU并联机构理论刚度模型的正确性。通过在ANSYS软件中建立有限元模型进行对比验证。在有限元模型中，定平台、动平台和所有运动关节均设为刚性。2-UPR-PRU并联机构中的杆件长度和材料参数如表1所示，需要注意的是此处3个运动分支的横截面均设为相同大小的圆截面，且各分支的弹性模量和剪切模量相同。

表1 2-UPR-PRU并联机构的长度及材料参数Tab.1 Length and material parameters of 2-UPR-PRU parallel manipulator

由于使用有限元模型计算2-UPR-PRU并联机构工作空间中所有点的刚度是一个耗时且困难的过程，因此选取位型和外载不同的3个示例进行结果验证，如表2所示。通过建模分析，可得到ANSYS软件中3个示例的变形结果，包括线性变形和角度变形，如图5所示。另外，表3为2-UPR-PRU并联机构动平台原点o的理论模型变形结果和有限元仿真变形结果，可以发现两个模型的结果基本一致，3个示例中所有的变形相对误差均不超过0.78%。

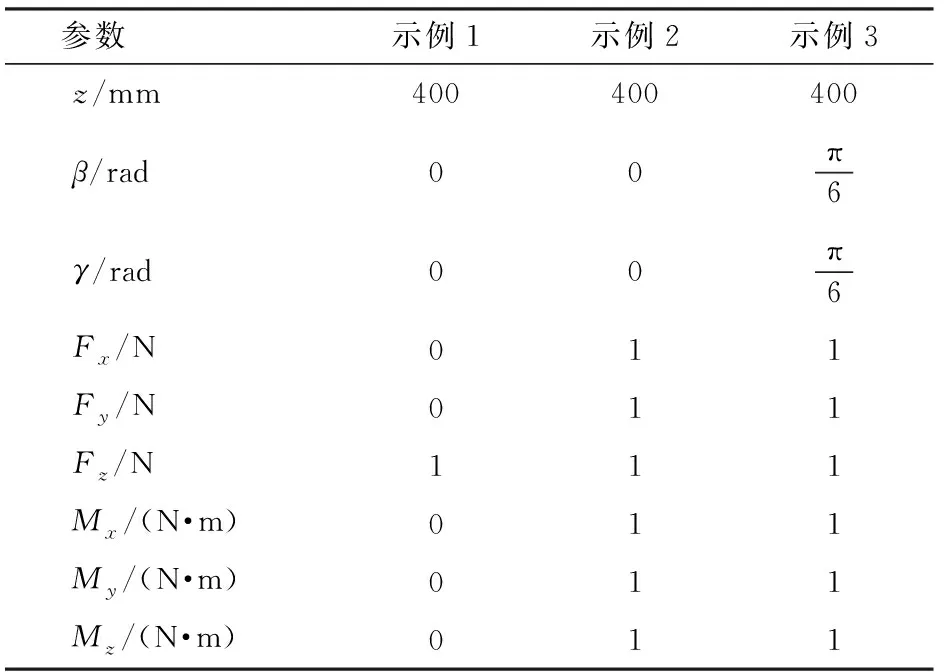
表2 2-UPR-PRU并联机构的3个选择示例Tab.2 Three selected cases of 2-UPR-PRU parallel manipulator

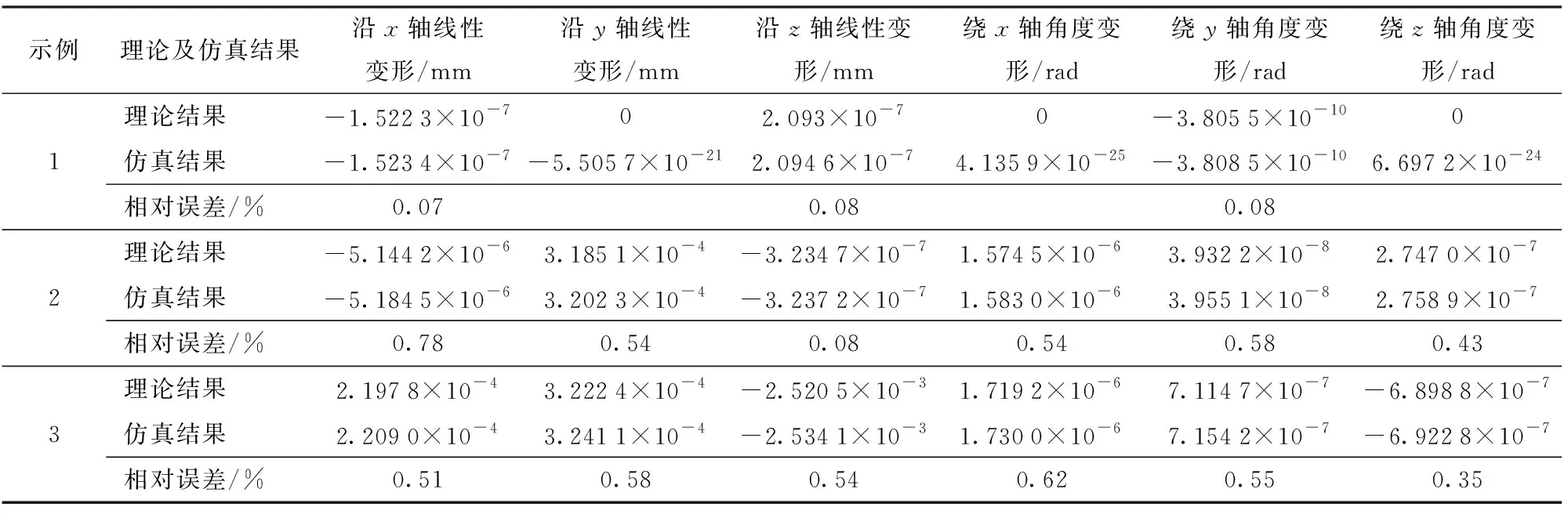
表3 2-UPR-PRU并联机构理论结果和仿真结果的变形对比Tab.3 Deformation comparison between theoretical and simulation results of 2-UPR-PRU parallel manipulator

除了对比变形结果，也可通过对比两种模型的整体柔度矩阵来验证理论模型的正确性。以示例3为例，其整体理论柔度矩阵和仿真柔度矩阵分别为

(23)

(24)

两个柔度矩阵中各个元素的相对误差为

(25)

从式(25)可以发现，所有相对误差均不超过0.60%，是可接受的。上述两个对比结果均证明了2-UPR-PRU并联机构理论静刚度模型的正确性，其可替代ANSYS软件的分析结果，为后续的静刚度性能分析提供保障。

3 静刚度性能分析

利用VSI[28]评估2-UPR-PRU并联机构静刚度性能。不同于其他基于刚度矩阵代数特性的刚度指标，VSI可通过能量来描述机构的刚度性能，且其与外部载荷的大小和方向直接相关，避免了刚度矩阵内元素量纲不同所带来的问题。在外载W作用下，并联机构的虚功WV可表示为

WV=WTD

(26)

将式(20)代入式(26)中，虚功WV可表示为

WV=WTK-1W

(27)

根据式(27)虚功刚度指标VSI可定义为

κ=1/(WTK-1W)

(28)

尽管刚度矩阵K中的元素具有不同的量纲，但VSI将其混合的单位转换成了J-1，可用于直接测量机构抵抗变形的能力。显而易见，κ越大，机构在该位型下的刚度性能越好。

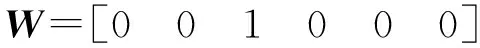
4 结论

(1)基于螺旋理论和应变能方法建立了2-UPR-PRU并联机构的分支和整体静刚度模型，建模简单，表达直接且含意清晰。

(2)以机构动平台的变形和整体柔度矩阵为验证对象，和有限元模型的仿真结果进行对比，结果表明理论刚度模型变形和柔度矩阵元素的相对误差分别不超过0.78%和0.60%，验证了2-UPR-PRU并联机构理论静刚度模型的正确性，可用于替代ANSYS软件进行机构的刚度分析。

(3)以VSI对2-UPR-PRU并联机构进行静刚度性能分析，确定了操作高度以及外载大小和方向对2-UPR-PRU并联机构刚度性能的影响，为样机设计提供参考。