苹果货架期GAN-BP-ANN预测模型研究

马惠玲 曹梦柯 王 栋 邱凌雨 任小林

(1.西北农林科技大学生命科学学院， 陕西杨凌 712100; 2.西北农林科技大学园艺学院， 陕西杨凌 712100)

0 引言

我国苹果年产量约占世界总产量的50%[1]。准确预测货架期能有效减少贮藏损失，保障上市果实品质。在苹果保鲜技术的研究中，通常测定失重率、可溶性固形物含量、可滴定酸含量、硬度、色值、抗坏血酸含量等品质指标来衡量保鲜效果[2-5]。因此，有望从中筛选特征指标或组合来用于采后苹果的货架期预测。目前在一些果蔬上已成功运用品质指标来构建货架期预测模型[6-8]。

广泛应用于货架期预测的模型主要包括传统的动力学模型以及机器学习模型等。前人对苹果采后品质指标变化也进行了探究，以及建立了Arrhenius货架期预测方程，但预测准确率较低[9]，说明常用的动力学模型难以表征苹果采后品质综合变化的复杂性，从而使其预测误差率较高。机器学习模型如反向传播人工神经网络(Back propagation-artificial neural networks, BP-ANN)已经广泛应用于农产品[10-12]的货架期预测问题上。然而，由于机器学习模型的复杂性，小样本数据集容易造成过拟合、欠拟合现象。扩充数据集，可以在一定程度上降低过拟合现象，提高模型预测的准确率。SMOTE(Synthetic minority over-sampling technique)及其改进算法的数据合成方法属于线性插值法，其合成的数据和实际数据相关性不强[13]。生成式对抗网络(GAN)模型是一种基于深度学习的数据生成方法，其基于博弈理论的数据生成原理，并采用无监督的学习方法，能自动对数据集进行学习，生成高质量的数据[14]。目前GAN已经应用于在一些小规模样本生成问题上[13,15-17]，暂未发现其用于果蔬理化指标数据的生成。

“富士”作为苹果中的优良品种，在我国和日本的种植比例都高达50%以上[18]。本文使用GAN提升BP-ANN模型的预测性能，基于苹果贮藏期间的真实数据来生成采后“富士”苹果的理化品质指标、贮藏温度及货架期数据，扩大BP-ANN的训练样本集数量，结合不同的变量排序方式对品质指标进行排序，分别建立品质指标和贮藏温度作为输入变量的货架期预测模型。

1 材料与方法

1.1 材料与处理

分别于2016—2018年10月10—11日在陕西省渭南市白水县某果园采收达到商品成熟期的套袋栽培的“富士”苹果(采收前7 d脱去最后一层半透明果袋)，选取果形规整、表面光洁、大小均匀的套袋果，去果袋，单果套发泡网，运回西北农林科技大学(3 h)。于0℃冷库预冷24 h，散去田间热量，再分别在温度0、5、15、25℃和相对湿度 85%～90%的条件下贮藏，所有果实均装于加有厚度11 μm塑料内衬袋的果框内，袋口松散折叠以保湿。0℃贮藏果前72 d每12 d取样一次，后198 d每24 d取样一次；5℃贮藏果前63 d每9 d取样一次，后108 d每18 d取样一次；15℃果每6 d取样一次，25℃果每3 d一次。每次取样随机抽取12个果实，以4个为一组建立3个生物学重复，用于在贮藏期间的各品质指标测定。

1.2 货架期苹果理化品质测定

1.2.1颜色参数

使用白板校准后的CR-400型色差计 (日本Konica Minolta公司)，分别用果实赤道线均匀的5个点来测定果实的颜色参数(亮度L、红绿度a、黄蓝度b)。总色差ΔE和饱和度C计算公式为

(1)

(2)

式中L0、a0、b0——颜色参数初始值

1.2.2硬度

沿苹果果实赤道线的阴阳两面各取两点削去1 cm×1 cm果皮，然后采用GY-3型果蔬硬度计(意大利Aldo Brue公司)测定硬度，单位为N/cm2。

1.2.3可溶性固形物含量、可滴定酸含量和固酸比

沿果实的赤道面，随机选取3个点，每个点去皮后各取10 g果肉，用榨汁机榨出汁，用吸管吸取3滴果汁，使用SW-LB32T型折光仪测定苹果的可溶性固形物含量，用质量分数表示。取剩余的果汁，采用酸碱滴定法测定可滴定酸含量[19]，用质量分数表示。固酸比为可溶性固形物与可滴定酸质量分数的比值。

1.2.4抗坏血酸含量

随机称取苹果鲜样5 g,采用钼蓝比色法[20]测定果实中还原型抗坏血酸的质量比，单位为mg/kg。

1.2.5淀粉含量

随机称取苹果鲜样1.5 g,采用硫酸蒽酮法[21]测定果实中淀粉质量比,单位为g/kg。

1.2.6质量损失率

每次取样时称取苹果的鲜质量，以质量随时间下降的百分比计算质量损失率。

1.3 货架期苹果感官品质的观测与评定

请10名经过专业培训的人员，对每次取样的12个果实进行品尝和感官品质评分，参照文献[22]的评定项目和权重，每批果实的得分值为10个品尝员评分的平均值。

1.4 数据处理

1.4.1理化品质指标排序

(1)稀疏主成分分析

稀疏主成分分析是在主成分分析的基础上引入带有稀疏度的惩罚系数或者不同的系数约束条件，使得到的部分载荷向量为零，从而得到稀疏的主成分[23]。

(2)ReliefF算法

ReliefF算法最早由文献[24]提出,最早用于解决二分类问题，ReliefF算法是公认的效果较好的Filter式特征评估算法。其关键思想是根据属性的值对实例的区分程度去估计这个特征区分邻近样本的能力，特征选择的思路是选取一个特征子集，使得特征子集上的分类错误率最小[25-26]。预测的品质指标权重通常取决于最近邻的数量，在本研究中，一共有12个品质指标，将最近邻分别设置为从2到11的数，计算预测权重平均值来作为最终结果，其权重即代表品质属性的重要程度，权重越大，则该品质属性越重要。

1.4.2附加GAN的BP-ANN货架期预测模型

生成式对抗网络(GAN)是由文献[27]提出的基于博弈论的生成式深度学习算法。GAN的一般结构如图1所示，主要由生成器和判别器两部分组成。由生成器接收随机噪声数据，真实数据的标签为0，生成数据的标签为1，由判别器判别是真实数据还是生成器生成的数据，判别器的损失函数为一个二分类模型，可通过交叉熵计算目标函数，其损失函数为

(3)

式中G、D——生成器和判别器的可微函数

E——目标函数的期望值

x——真实样本数据

z——随机噪声

G(z)——判别器的生成数据

下角标x～Pdata(x)表示x采样于真实数据分布Pdata(x)，z～Pz(z)表示z采样于真实数据分布Pz(z)。

第1项代表D判断出x是真实数据的情况，第2项代表D判断数据是否是由生成器G将噪声矢量z映射而成的生成数据。G和D进行二元零和博弈，GAN算法的流程为先固定生成器优化判别器，使得判别器的判别准确率最大化，然后固定判别器，优化生成器使得判别器的判别准确率最小。当且仅当Pdata(判别真实数据的准确率)等于Pg(判别生成数据的准确率)时达到全局最优解。

生成器和判别器均采用全连接网络结构。生成器是由两层感知机组成，其输入为随机噪声，第1层其激活函数为ReLU，由 25个隐藏层神经元组成，第2层其激活函数为Linear，输出维度为14的数据。判别器也是由两层感知机组成，其输入为真实数据和生成器生成的假数据，第1层由25个神经元组成，其激活函数为ReLU，第2层由1个神经元组成，其激活函数为Sigmoid。每训练3 000次，保存一次模型。文献[15]通过直接观察生成的菌菇表型图像数据来选择GAN生成的图像；文献[13]根据鸭蛋的蛋形指数来选择GAN生成的数据；文献[17]根据模型预测的准确率来判断GAN模型对于长短期记忆网络(LSTM)的改进作用，从而选择GAN生成的数据。在本研究中，苹果的品质指标取值均随着贮藏时间的变化而变化，而且品质指标无法像图像一样可以直接观察，因此通过GAN的判别器判别真实数据和生成数据的准确率对生成数据进行初次选择，并通过绘图的形式，将生成数据和真实数据的取值范围进行比较，再通过 GAN-BP-ANN模型预测货架期的准确性来再次判断GAN生成数据的质量。试验平台为Windows 10系统，8 GB内存，500GB SSD，1TB HD，Intel Core i5-5200U，2.20 GHz，Nvidia GeForce 930M,2 GB。算法采用Tensorflow V1.1GPU框架和Python 3.7实现。

BP-ANN模型是一种误差反向传播的模型，其通常由输入层、隐藏层和输出层3层组成。在此研究中，将品质属性和贮藏温度作为输入层，货架期作为输出层。将得到的品质指标，按照其排序结果，从1到12逐一叠加，再组合贮藏温度，作为输入变量分别建立扩充数据集的GAN-BP-ANN和未扩充数据集的BP-ANN货架期预测模型。从图2可以看出，基于GAN改进的BP-ANN模型结构将GAN生成的最优解和真实测定的数据同时作为BP-ANN的输入层，BP-ANN模型第1层的激活函数为Tansig，第2层的激活函数为Purelin，若在最大迭代次数内未达到训练目标，则根据相应规则对参数进行优化，如果达到训练目标，则保存模型，并根据保存的模型对验证集进行预测。训练目标为0.000 1，学习率为0.01，最大迭代次数为1 000。 由于其初始化的权值和阈值对网络的性能具有较大的影响，在此研究中通过多次建模来选择最优的权值和阈值。

采用平均相对误差和决定系数(R2)作为模型准确性的评价标准，建模过程通过Matlab 2019a软件实现，在进行建模前，将所有数据进行归一化处理。

2 结果与分析

2.1 不同温度下苹果品质指标的变化趋势

考虑到生产上采用冷藏、气调贮藏苹果的温度通常在0℃，采用自然低温贮藏时在5～15℃，消费者在室温存放又常为20～25℃，因此，苹果采后可能存在的环境温度为0～25℃范围内的任意温度，本研究选定其中的4种特征温度进行仿真试验。

从图3可看出，0℃下贮藏的苹果12种品质指标变化速率最慢，随着温度的升高，变化速率加快。各指标在不同温度下的变化总趋势一致，表现为3种类型：①渐降型。首先是可溶性固形物含量，各组可溶性固形物含量在第2个观测点均出现短暂上升，这是果实采后初期淀粉等多糖降解量较大，可溶性糖的积累大于消耗，使其总量增加所致。而采后可溶性糖主要是作为呼吸底物而被消耗[28]，因此，贮藏(货架)全程呈现总体下降趋势。其次，可滴定酸和还原型抗坏血酸含量也全程下降。抗坏血酸作为一种抗氧化剂，能清除机体内活性氧，延缓衰老[29-30]，其在中性和碱性环境下极易被氧化，它和可滴定酸总量的含量逐渐减少意味着苹果果实贮藏过程中除了酸味会变淡外，果实营养品质也在下降；淀粉作为果实细胞重要的贮藏性物质，其降解与果实的软化有关[31]。②上升型。质量损失率呈现上升趋势，导致果实质量损失的原因主要是水分的丧失和呼吸消耗[32]。随着贮藏温度的升高和贮藏时间的延长，黄蓝度b、总色差ΔE、色彩饱和度C总体呈现上升状态，主要是由于在贮藏期间叶绿素逐渐被降解[33]，反映了苹果的底色逐渐黄化，光泽变暗。③起伏+渐变型。硬度在前7个观测点和a、L在前3～5个观测点取值均呈起伏式变化，以后缓慢下降，虽然随着贮藏时间的延长，果胶物质逐渐被细胞壁酶降解，细胞壁结构逐渐发生变化，果实的硬度总体下降[32]，但是，不同苹果采后硬度下降快慢不同，“富士”苹果以其“宁烂不绵”而著称，此文结果从数据上展示了该品种硬度在贮藏全程下降慢的属性；5～25℃组的前3个观测点均表现a先上升再下降，对应地，L先下降再上升，可见，苹果采后在货架期红度短暂增大，亮度短暂下降，这与果实采后后熟有关[33]。“富士”苹果果实的这种变化特性在其它研究中也有所报道[29，34]。0℃组可溶性固形物含量和a的初期变化幅度小，L却也先急降后上升，表明除了与红度有关外，L还受到果面其它属性，如果粉厚度等影响，是与糖分、红绿度不完全相关的独立属性。

2.2 品质指标重要性排序结果

在建立货架期预测模型时，用简化的数据集作为模型的输入变量可以节省运算时间和预算。稀疏主成分分析(SPCA)和ReliefF算法对品质指标进行排序的标准不同，SPCA算法是将高维数据向低维子空间映射降维，ReliefF算法侧重于自变量对因变量的区分程度。表1列出这2种分析方法对品质属性的排序结果，可以看出，两种排序结果有很大区别，SPCA中，当k=1时，得到的排序第一的品质指标为质量损失率。ReliefF算法中，与货架期关联度最大的为L。

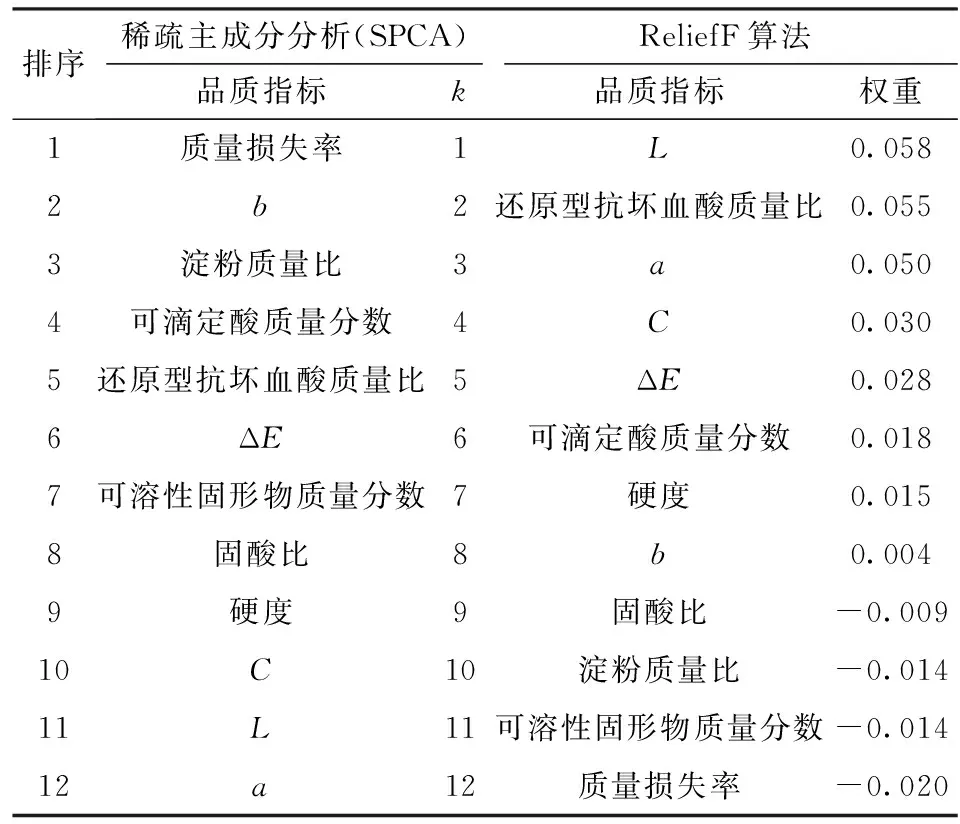
表1 2种特征提取方法得到的品质指标排序结果Tab.1 Ranking of quality attributes obtained by three feature extraction methods

2.3 附加GAN的BP-ANN货架期预测模型构建

2.3.1GAN生成的有效数据

在构建预测模型时，数据集越大，预测模型能学习到的特征越多并且越准确，从而越能避免模型的过拟合和欠拟合现象，使得模型的预测准确性越高。而实际上，经常由于试验材料、经费等众多问题使试验获得的数据集较小。生成式对抗网络(GAN)是一种深度学习算法，其通过生成器和判别器互相博弈来提高生成数据的准确性。随着迭代次数的增加，GAN的生成器会生成不同的数据。在此研究中，为了使品质属性的取值更加可靠，将年份之间作为重复，获得的理化指标和对应货架期的平均值数据为51组，判别器对此真实数据和生成数据判别准确率如图4所示。可以看出，随着迭代次数的增加，判别准确率逐渐接近于0.50，当迭代次数为33 000次时，判别真实数据的准确率为0.51，判别生成数据的准确率也为0.51，均最接近于0.50，继续增大迭代次数至2.0×105，判别器对两组数据判别准确率偏差增大，说明迭代次数为33 000时的生成器和判别器之间已经接近纳什均衡，即生成数据与真实数据已经非常相似。由图5(图中参数序号1～14分别表示硬度(N/cm2)、可溶性固形物质量分数(%)、可滴定酸质量分数(%)、固酸比、还原型抗坏血酸质量比(mg/kg)、淀粉质量比(g/kg)、质量损失率(%)、L、a、b、ΔE、C、贮藏温度、货架期)显示，生成数据各指标取值均在真实数据取值范围之内，直观表现了二者的相似性。由于前人的研究均没有对GAN生成数据的合理量有具体约定[13-15]，故选择迭代次数33 000次时生成的38组数据作为通过GAN进行数据生成的结果，用于后续的模型构建。

按训练集和验证集为3∶1的比例进行建模和验证，训练集经生成式对抗网络(GAN)扩充得到的38组生成数据不用于验证集验证，即分别采用真实数据的3/4(38组)、真实数据+生成数据(76组)作为训练集，选取每个贮藏温度下的剩余的1/4组数据(其中25℃共4组数据，其它3个温度各3组)，共13组真实数据作为验证集来构建BP-ANN和GAN-BP-ANN货架期预测模型。

2.3.2GAN对ReliefF-BP-ANN预测货架期准确性的影响

为了评估GAN对于 BP-ANN货架期预测模型的改进作用，分别按照ReliefF排序方法的结果，将1～12个品质指标依次累加，再加上贮藏温度作为输入层变量，分别建立经过训练集扩充的ReliefF-GAN-BP-ANN模型和未经训练集扩充的ReliefF-BP-ANN模型。为了有效评估GAN的作用，均将各个模型重复训练100次，取其平均值作为最后的结果，模型的最大训练次数、学习率和激活函数均相同。由表2可知，ReliefF-GAN-BP-ANN模型其训练集平均相对误差在0～0.095之间，ReliefF-BP-ANN模型其训练集平均相对误差在0～0.112之间，ReliefF-GAN-BP-ANN相比ReliefF-BP-ANN模型，其建模效率没有明显的改善。由图6可直观地看出，采用ReliefF-GAN-BP-ANN模型其验证集的平均相对误差均低于ReliefF-BP-ANN模型，决定系数均高于ReliefF-BP-ANN模型，表明附加GAN的BP-ANN模型(ReliefF-GAN-BP-ANN)对本研究中建模较单独采用ReliefF-BP-ANN的准确度有明显提高，有效地增加了模型的预测准确率，说明GAN生成数据的有效性及增大数据集改进BP-ANN预测货架期的准确性。由图6可知，用ReliefF对品质指标进行排序后，分别构建ReliefF-BP-ANN和ReliefF-GAN-BP-ANN模型，当采用排序前8的8个品质指标即L、还原型抗坏血酸含量、a、C、ΔE、可滴定酸含量、硬度、b和贮藏温度作为ReliefF-GAN-BP-ANN的输入变量时，验证集中13组数据的预测值与真实值的平均相对误差最小，为0.154，决定系数为0.957。

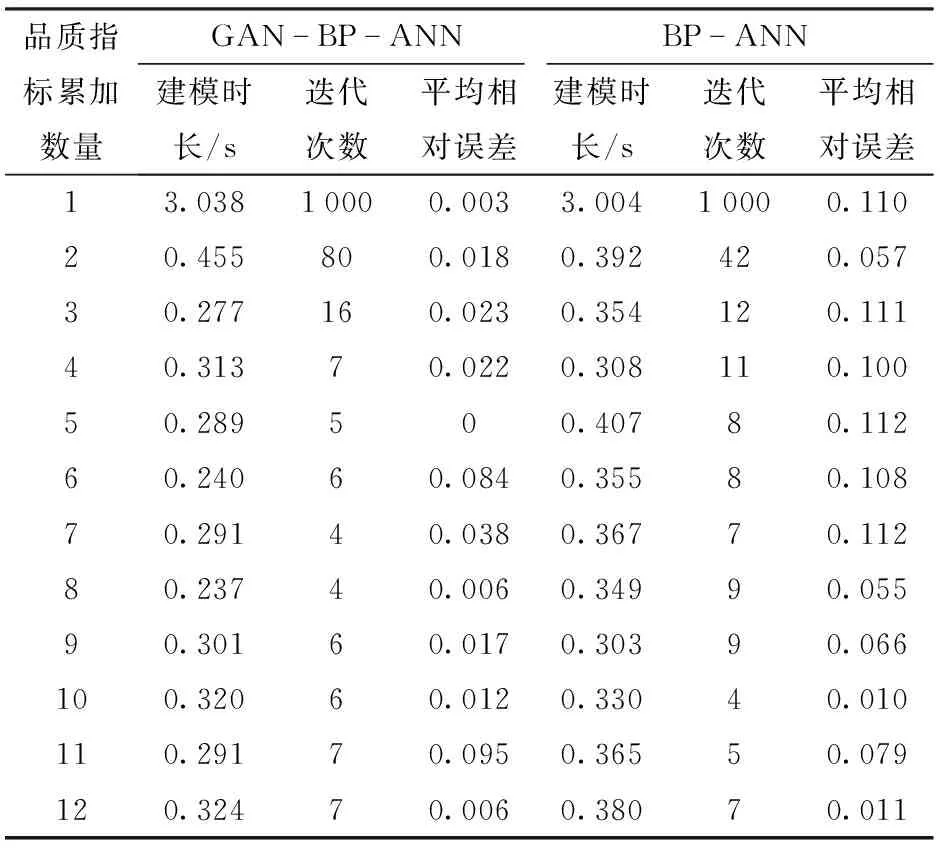
表2 采用ReliefF排序方法构建GAN-BP-ANN和BP-ANN模型训练集的平均相对误差Tab.2 Mean relative error of GAN-BP-ANN and BP-ANN model training set based on ReliefF

2.3.3GAN对SPCA-BP-ANN预测货架期准确性的影响

按照SPCA排序方法的结果，将1～12个品质指标依次累加，再加上贮藏温度作为输入层变量，分别建立经过训练集扩充的SPCA-GAN-BP-ANN模型和未经训练集扩充的SPCA-BP-ANN模型。均将各个模型重复训练100次，取其平均值作为最后的结果，模型的最大训练次数、学习率和激活函数均相同。由表3可知，SPCA-GAN-BP-ANN模型其训练集平均相对误差在0～0.018之间，SPCA-BP-ANN模型其训练集平均相对误差在0～0.019之间，均小于ReliefF-GAN-BP-ANN和ReliefF-BP-ANN模型，SPCA-GAN-BP-ANN相比SPCA-BP-ANN模型，其建模效率没有明显的改善。由图7可见，采用SPCA-GAN-BP-ANN模型其验证集的平均相对误差也均低于SPCA-BP-ANN模型，决定系数也均高于BP-ANN模型。当采用排序第1的品质指标即质量损失率和贮藏温度(D1组)一起作为GAN-BP-ANN的输入变量时，验证集中13组数据的预测值与真实值的平均相对误差最小，为0.052，决定系数为0.989。当采用排序前2的两个品质指标和贮藏温度作为输入层时，即质量损失率、b和贮藏温度(D2组)作为GAN-BP-ANN的输入变量时，验证集中13组数据的预测值与真实值的平均相对误差为0.064，决定系数为0.990。当采用排序前6的6个品质指标即质量损失率、b、淀粉含量、可滴定酸含量、还原型抗坏血酸含量、ΔE和贮藏温度(D3组)作为GAN-BP-ANN的输入变量时，验证集中13组数据的预测值与真实值的平均相对误差为0.070，决定系数为0.992。综合可知，2种特征选择方法中，SPCA通过特征累加所构建的模型其验证集平均相对误差最小，通过SPCA挑选出3组GAN-BP-ANN建模的特征品质指标，即：质量损失率和贮藏温度(D1组)；质量损失率、b和贮藏温度(D2组)；质量损失率、b、淀粉含量、可滴定酸含量、还原型抗坏血酸含量、ΔE和贮藏温度(D3组)，其验证集中13组数据的相对误差分别为0.052、0.064和0.070，低于BP-ANN的0.109、0.104和0.115，即附加GAN的模型把预测准确度从平均0.891提高到0.938，提高了0.047；验证集中预测值和真实值决定系数R2分别为0.989、0.990和0.992，大于等于未附加GAN模型的0.989、0.963和0.991。这说明输入层为D1、D2和D3组所构建的GAN-BP-ANN模型可以较为准确地预测采后苹果的货架期。

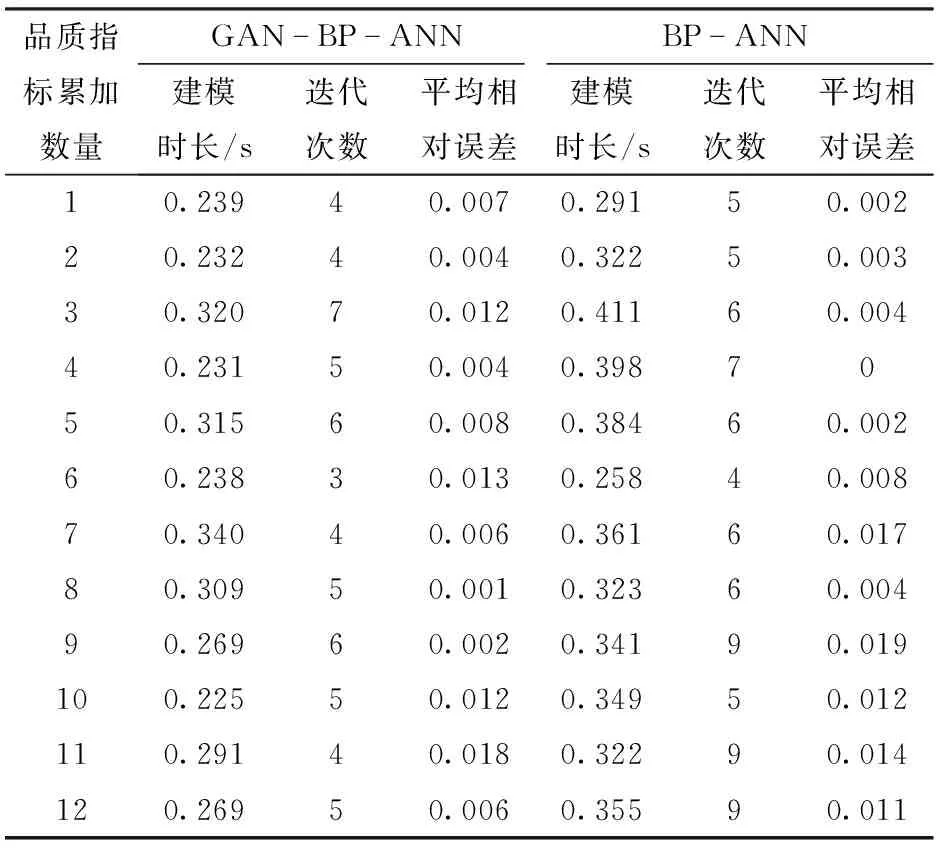
表3 SPCA排序方法构建GAN-BP-ANN和BP-ANN模型训练集的平均相对误差Tab.3 Mean relative error of GAN-BP-ANN and BP-ANN model training set based on SPCA

2.3.4GAN-BP-ANN模型与其它货架期预测模型的比较

常用的货架期预测模型还包括多元线性回归(MLR)、决策树(DT)和支持向量机(SVM)等。分别建立品质属性与货架期之间的多元线性回归(MLR)、决策树(DT)模型和支持向量机(SVM)等，使用上述通过SPCA得到的最优模型的输入变量作为输入变量，即分别使用质量损失率和贮藏温度(D1组)；质量损失率、b和贮藏温度(D2组)；质量损失率、b、淀粉含量、可滴定酸含量、还原型抗坏血酸含量、ΔE和贮藏温度(D3组)作为输入变量，其训练集和验证集平均相对误差和决定系数如表4所示,可以看出其训练集和验证集的平均相对误差均比较高，决定系数均比较低。上述选出的最优模型其性能均优于MLR、DT和SVM。

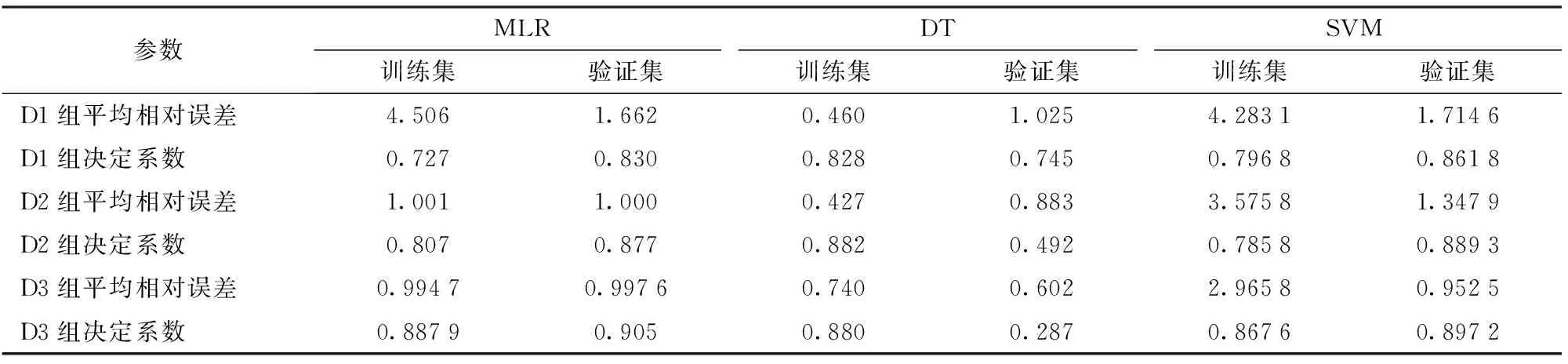
表4 多元线性回归(MLR)、决策树(DT)和支持向量机(SVM)货架期预测模型训练集和验证集的平均相对误差和决定系数Tab.4 Mean relative error and determination coefficient of training set and validation set of multiple linear regression (MLR), decision tree (DT) and support vector machine (SVM) shelf-life prediction models

3 结论

(1)采用GAN法对观测数据集进行扩充，迭代次数33 000次时生成器和判别器之间接近纳什均衡，生成数据均在真实数据的分布范围之内。

(2) 2种变量排序法下，均以附加GAN的BP-ANN所建模型对货架期的预测准确度高。且以SPCA法排序结果构建GAN-BP-ANN模型的平均相对误差较ReliefF更低，部分验证集的平均相对误差均在0.07以内，比未附加GAN的BP-ANN模型预测准确度提升了0.047。结合SPCA法特征变量选择的GAN-BP-ANN模型被确定为预测苹果货架期的有效方法。