基于NOMA的5G超密网计算迁移与资源分配策略

时永鹏，张俊杰，夏玉杰1，，高雅1，，张尚伟

（1.河南省电子商务大数据处理与分析重点实验室（洛阳师范学院），河南洛阳 471934；2.洛阳师范学院物理与电子信息学院，河南洛阳 471934；3.西北工业大学网络空间安全学院，西安 710072）

0 引言

5G 网络的快速发展为人们提供了诸如虚拟现实、自动驾驶等众多具有广泛前景的应用和服务，这些应用和服务除了需要高效可靠的通信资源外，也需要大量的计算资源［1］。然而由于移动设备的电池容量和计算能力有限，仅仅依靠设备本身的资源很难完成对这些计算密集型应用的处理。云计算虽然可以显著降低用户的计算延迟和能耗，但由于终端用户与云服务器之间的传输距离较长，无法满足时延敏感型应用的需求［2］。为了解决这个问题，移动边缘计算（Mobile Edge Computing，MEC）［3］被提出并得到了广泛研究，通过计算迁移，部署在网络边缘的计算资源可以为移动设备提供高效和灵活的计算服务。

作为5G 系统中的一种新的网络架构，超密网（Ultra dense Network，UDN）［4］通过在网络区域内大量部署短距离、低功率的小基站，可以为用户提供吞吐率高、灵活性强的无线数据传输服务。同时，非正交多址接入（Non-Orthogonal Multiple Access，NOMA）也被视为5G 的关键候选技术之一，以解决4G 网络中正交多址接入（Orthogonal Multiple Access，OMA）频谱效率低的问题。NOMA 在发射端使用叠加编码技术，在接收端则用串行干扰消除技术实现正交解调，从而在同一个子信道上允许多个用户叠加［5］。在5G 系统中，UDN、NOMA 技术与MEC 的有机结合，做到优势互补，不但能为移动用户提供稳定、可靠的数据通信，提高频谱效率，还能通过计算迁移，减少数据传输和处理时延，降低终端能耗。

目前针对基于NOMA的边缘网络中的计算迁移研究已经取得了一些重要研究成果，这些研究工作主要在时延约束下最小化设备的计算能耗或时延与能耗的加权代价。文献［6］提出了一种启发式算法，通过优化用户分组、传输功率和计算资源，以最小化5G 网络中设备的能量消耗。文献［7］以减少用户的任务卸载时延为目标，综合考虑计算迁移决策和资源分配，提出了一种基于匹配理论的联合优化算法。但上述两项工作均考虑的是单基站场景。而在5G 超密网中，文献［8］在获取设备NOMA 分组的基础上，采用深度确定性策略梯度算法在提高传输功率的同时最小化设备的计算代价，然而该工作没有考虑子信道的带宽分配。文献［9］在采用NOMA 的异构边缘计算网络中，设计了一种基于序列凸规划的算法联合优化功率分配、通信资源和计算资源，从而获得最低计算能耗。在基于NOMA 的超密集异构网中，文献［10］通过构建效用函数，提出了一种量子粒子群优化算法在对子载波和传输功率进行优化分配的同时最大化计算迁移的能量效率，和文献［9］类似，虽然考虑了无线资源优化，但缺少有效的用户分组。文献［11］则将超密网中的计算迁移定义为一个混合整数非线性规划，并提出了一个基于遗传算法的基站分组和存储资源分配策略，从而最小化所有计算任务的处理时延。

显然，现有基于NOMA 的超密网中的计算迁移研究工作都提出了有效的解决方案，但它们均存在一些问题，要么没有考虑到网络中子信道的带宽分配，要么忽略了设备的分组匹配。因此，本文提出了一种基于NOMA 的5G超密网计算迁移与资源分配策略，以优化设备计算代价为目标，综合考虑迁移策略、带宽优化与分组匹配。具体工作如下：

1）在基于NOMA 接入的5G 超密网中，以计算时延和能耗的不同权重构造计算代价函数，并以此为最小化目标将计算迁移定义为一个约束最优化问题；

2）设计联合优化策略，通过交替使用模拟退火技术、内点法和贪心算法，对计算迁移、带宽分配和分组匹配进行迭代求解，最终获得最低计算代价。

仿真实验结果表明所设计的联合优化策略能有效降低设备的计算代价，且具有良好的收敛性。

1 基于NOMA的5G超密网计算迁移

1.1 系统模型

考虑如图1 所示的5G 超密网架构，N个移动设备（N={1，2，…，N}）采用随机形式分布在由M个小基站（M={1，2，…，M}）所覆盖的网络区域。小基站上均部署有边缘服务器，可为接入设备提供计算服务。所有小基站均采用NOMA 技术，共享总带宽为W的频率资源。若设备与基站通信过程中保持位置不变，则被基站m服务的设备集合可表示为，其中|Cm|表示Cm中设备的个数。系统中共有K个无线子信道（K={1，2，…，K}），将Cm中利用子信道k与基站m通信的设备作为一个NOMA 分组，其中∈{0，1}表示设备n是否属于Cm，k，如果是，则=1；否则。显然有：

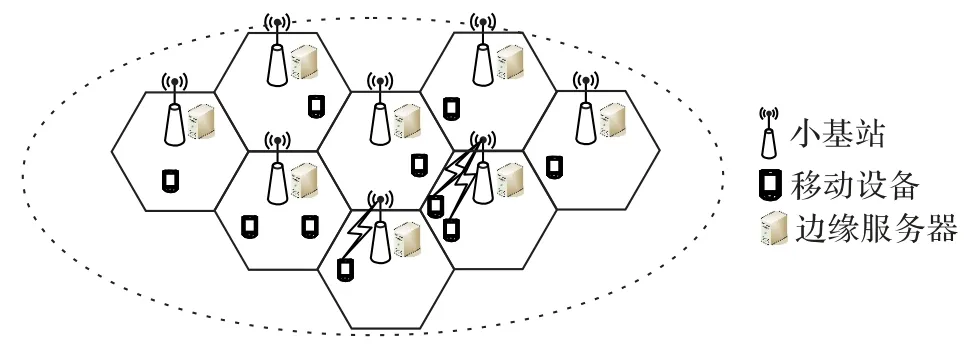
图1 5G超密网中的计算迁移架构Fig.1 Computation offloading architecture in 5G ultra-dense network

式中|Cm，k|表示Cm，k中设备的数目。

1.2 通信模型

1.3 计算模型

1.3.1 本地计算

1.3.2 迁移到小基站上的边缘服务器计算

1.4 问题定义

根据以上描述，本文要解决的主要问题可描述为：在基于NOMA 的5G 超密网中，给定系统的频谱资源、移动设备的计算能力、边缘服务器的计算能力等网络参数，设计最佳计算迁移、带宽分配与分组匹配策略，在满足计算任务最大时延的前提下，最小化设备的计算代价。为便于数学描述，设μ=为设备的计算迁移策略组合，ω={ωk}为带宽分配方案，λ=表示设备分组匹配策略，则该问题的形式化定义为：

在问题P1 中，约束条件C1 保证每个计算任务的处理时延不得超过其最大允许时延；C2 列出了计算任务的所有计算模式但每个任务只能选择其中一种；C3 是系统总带宽的约束条件；C4、C5则是移动设备与NOMA 分组的关系。容易证明，P1是一个NP-难问题［12］。

2 问题求解和算法设计

从式（10）中的约束C2 和C5 可以看出，P1 是一个混合整数非凸优化问题。为求解该问题，本文将P1分解成三个子问题：1）在给定设备分组匹配和带宽分配策略的前提下求解计算迁移策略μ；2）在给定计算迁移和设备分组匹配策略的情况下求解带宽分配策略ω；3）在计算迁移和带宽分配策略已知的条件下获取设备分组匹配策略λ。最后通过迭代的方法对这三个子问题进行联合优化，获得最小计算代价及最优计算迁移、带宽分配和分组匹配策略。

2.1 计算迁移策略优化

在给定设备的NOMA 匹配策略λ和带宽分配策略ω的前提下，P1 中的计算迁移策略优化是一个整数编程问题，可通过求解P1.1获得：

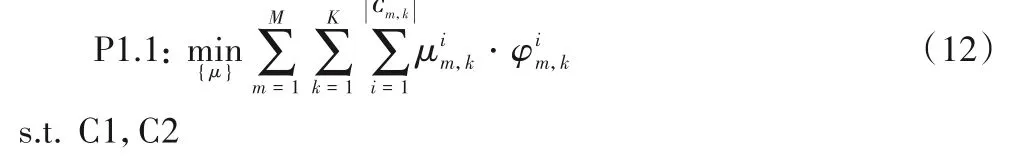
该问题可通过枚举的方法列举出N个设备的所有可能计算迁移策略组合，并从中选取计算代价最小的组合作为最优策略，但其计算复杂度高达O(2N)，在规模较大的网络中不适用。因此，本文设计了一个基于模拟退火技术的低复杂度计算迁移优化算法，在每次迭代中仅随机改变一个设备的计算迁移策略：

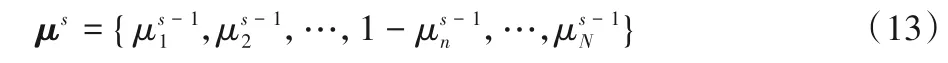
其中，μs-1为第s-1次迭代的计算迁策略。用F(μs)表示在迁移策略为μs时对应的P1.1中的目标函数值，当且仅当式（14）为负时设备n的策略改变才能生效，否则以概率接受μs为当前最优策略。

其中T为当前温度变量。本文算法的详细步骤如算法1所述。

算法1 基于模拟退火技术的计算迁移优化算法。

2.2 带宽分配策略设计

当计算迁移和分组匹配策略已知时，带宽分配策略可通过求解以下问题获得：

式（20）、（21）对ωk的二次导数均大于0，因此P1.2 的目标函数和约束C1均为ωk的非线性凸函数，可利用Matlab中的非线性优化函数fmincon 或在YALMIP 优化工具中利用内点法求解［13］。

2.3 设备分组匹配算法设计

给定计算迁移和带宽分配策略，设备分组匹配问题可定义为：

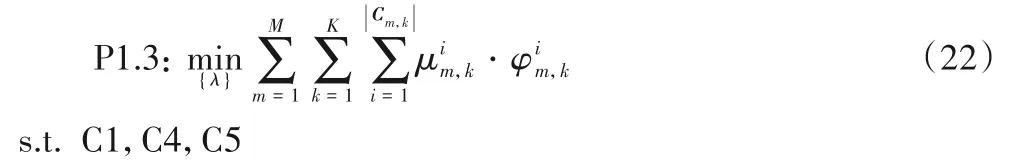
与P1.1类似，P1.3也是一个整数编程问题。考虑到分组匹配的目的是为了让设备在对应子信道上获得最大的数据传输速率，从而最小化计算时延和能量消耗。而在传输功率和子信道带宽一定的前提下，传输速率受信道增益的影响最大。由于同一NOMA 分组中设备间的信道增益差异越大，对信道容量的提升越大［14］，本文设计了一个基于贪心算法的分组匹配策略，即先将被同一基站服务的设备按信道增益降序排列，然后依次将每个设备匹配到能使其传输速率最大的NOMA分组中。详细的分组匹配过程如算法2所示。

算法2 基于贪心方法的设备分组匹配算法。

2.4 联合优化算法设计

通过求解子问题P1.1、P1.2 和P1.3，问题P1 的最优解可通过基于坐标下降法［15］的迭代算法对这三个问题交替求解获得。坐标下降法在连续迭代中通过依次求解一个变量而固定剩余变量的方法最小化目标函数。问题P1 含有三个变量(μ，λ，ω)，则在算法的每次迭代过程中，首先固定(λ，ω)求解μ，然后再给定(μ，λ)得到ω，最后由更新后的(μ，ω)获取λ。由于是最小化问题，因此在迭代中新的解应使目标函数值的变化沿下降方向，即：

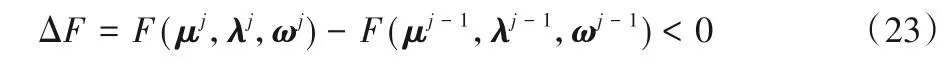
当目标函数值不再变化或者变化值在允许误差范围之内，即|ΔF|<ξ，或者达到迭代次数时，即可得到P1 的最优解。具体的求解过程如算法3所示。

算法3 联合优化算法。

2.5 算法复杂度分析

所提出的计算迁移和资源分配问题通过算法3 中的联合优化策略求解，而算法3 的主要迭代过程则是对三个子问题进行交替求解。算法1 中的while 循环的每一次迭代主要用来生成新的计算迁移策略并计算ΔF，而计算ΔF的复杂度为O(N2)，如果算法1中while循环的最大迭代次数为tmax，则该算法的计算复杂度为O(tmaxN2)。带宽分配优化子问题通过内点法求解，其复杂度为O(N2log(ξ-1))［16］，ξ为允许误差。算法2的计算复杂度为O(NMK)。因此，所提的联合优化算法每次迭代的计算复杂度为三个子过程的复杂度之和。如果通过Jmax次迭代获得最优解，则整个算法的计算复杂度为：O(Jmax(tmaxN2+N2log(ξ-1)+NMK))。

3 仿真实验与结果分析

3.1 参数设置

不失一般性，设20 个小基站部署在1 km2的区域内，每个小基站的覆盖半径为50 m，100 个移动设备随机分布在这些小基站的服务范围内。设备的传输功率100 mW～150 mW，CPU 频率为0.8 GHz～1 GHz。每个设备的计算任务的输入数据大小为500 KB～800 KB，所需要CPU周期为500 Megacycles～1000 Megacycles，最大允许处理时延为0.5 s～2 s。详细的参数设置如表1所示，所有仿真实验均在Matlab软件中进行。

表1 详细的仿真参数Tab.1 Detailed simulation parameters

3.2 仿真结果与分析

图2 是对所设计的联合优化算法的收敛性分析。从图2中可以看出，对于不同的设备和小基站数目，该算法均能在25 次迭代后获取最低的计算代价，表明了所设计算法具有良好的收敛性。从图2 中还可以看到，小基站数目越多，总的计算代价越低，这是因为更多的边缘服务器可以减低计算时延，从而减少计算代价。

图2 本文算法收敛性分析（α=0.5）Fig.2 Convergence analysis of proposed algorithm（α=0.5）

图3 为不同接入方式和带宽分配策略下的设备计算代价的比较。本文的主要目标是获取在基于NOMA 的5G 超密网中的最优计算迁移与带宽分配策略，因此为凸显NOMA 接入技术对超密网性能的有效提升以及在计算迁移中进行带宽分配的优越性，同时更好地验证本文设计的联合优化算法的性能，在仿真时选取了正交接入和非正交接入、带宽分配优化和平均分配带宽不同的方案进行对比。对于平均分配子信道带宽的情况，分别选择了文献［8］中的非正交接入和文献［17］中的正交接入两种计算迁移方案。此外还考虑了正交接入时带宽分配优化的场景。从图3 可以看出，总的计算代价随着设备数目的增加而单调增大。通过多种方案的对比可知，联合优化策略综合考虑了计算迁移、设备分组和带宽分配，极大提升了信道容量，降低了设备的计算代价。

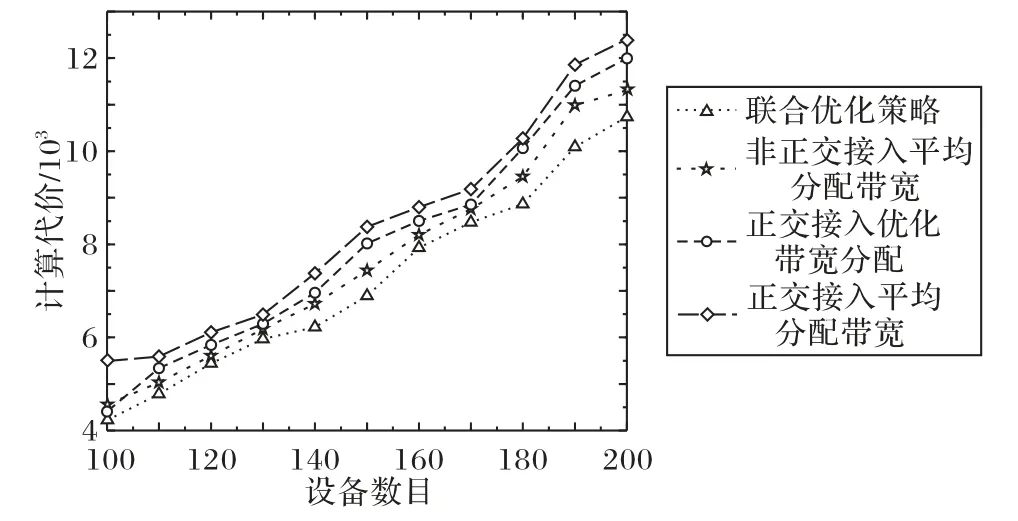
图3 不同接入技术和带宽分配策略下的计算代价对比（M=20，α=0.5）Fig.3 Comparison of computation cost under different access techniques and bandwidth allocation strategies（M=20，α=0.5）

图4 展示了不同的权重系数α对所有设备计算代价的影响。由图4 可知，随着α值的不断增大，时延在计算代价中的权重越来越大而能耗的权重则逐渐降低，总的计算代价则逐步减小。特别是当α=1时，计算代价只包括计算任务的处理时延，设备总的计算代价最小。因此，在进行计算迁移时，必须根据计算任务的类型设置适当的权重系数。

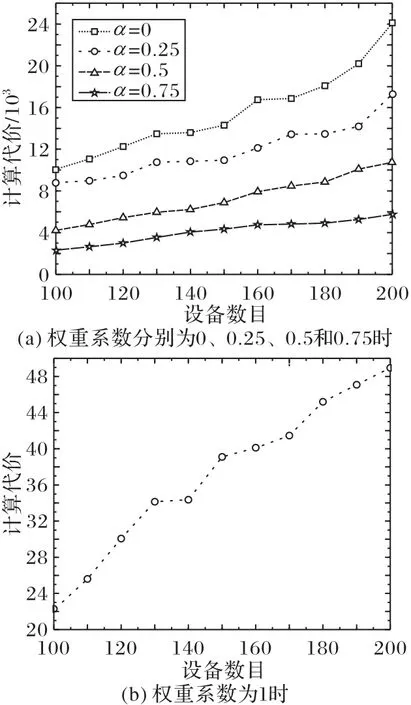
图4 权重系数对计算代价的影响（M=20）Fig.4 Effect of weight coefficient on computation cost（M=20）

图5给出了不同计算模式下设备计算代价的比较。

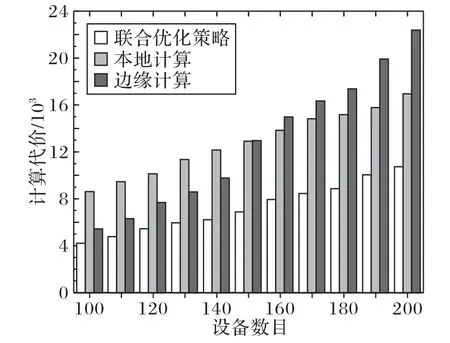
图5 不同计算模式下的计算代价对比（M=20，α=0.5）Fig.5 Comparison of computation cost under different computing modes（M=20，α=0.5）

从图5 中可知，当设备数目较少时，采用边缘服务器计算模式的代价远小于本地计算模式的代价，这主要得益于边缘服务器丰富的计算资源。然而随着设备数目的增多，使得同一NOMA 分组和不同分组同一子信道的干扰逐渐增大，从而降低了设备的数据传输速率，导致了更长的传输时延，增大了计算代价，而采用联合优化策略则可以获得最低的计算代价。

4 结语

针对基于NOMA 技术的5G 超密网计算迁移和带宽分配问题，以最小化设备的计算代价为目标，本文提出了一种联合优化策略。首先，将研究内容定义为约束非凸优化问题；然后，将其分解成计算迁移、带宽分配和设备分组匹配三个子问题分别求解；最后，利用联合优化算法对三个问题用迭代方法交替优化并得出最优解。实验结果表明，所提出的策略具有良好的收敛性，且能获得最优的计算迁移和带宽分配方案，以及最低的设备计算代价。