三因子匿名认证与密钥协商协议
张 平,贾亦巧,王杰昌,石念峰
(1.河南科技大学数学与统计学院,河南洛阳 471023;2.郑州大学体育学院计算机教研室,郑州 450044;3.东部战区总医院,南京 210002)
0 引言
作为信息安全的一个重要研究领域,认证与密钥协商(Authenticated Key Agreement,AKA)协议可使通信方之间建立共享会话密钥,并以此实现开放网络中的安全通信[1]。随着移动通信与网络技术的飞速发展,现如今AKA 协议已被广泛应用于许多实际场景,如电子政务、社交通信以及金融交易等。但由于通信信道中仍存在各类非法攻击,因此,如何确保客户与服务提供方之间进行可靠的双向认证并建立安全会话已成为亟须解决的问题。
Lamport[2]于1981 年最先设计了一种基于口令的远程客户身份认证协议,该协议具有较强的实用性,但存在被盗校验值攻击。因而,一些研究者提出了基于口令的能抵御此类攻击的认证协议[3-4],这些协议虽然便于管理,但存在熵值较小、易遭受字典攻击[5]等安全弊端。为解决单一口令所造成的安全性问题,研究者们又设计了各种基于口令和智能卡的双因子认证协议[6-10],这些协议提升了认证过程的安全性,但因口令易被遗忘、泄露,智能卡易被遗失、窃取,仅将口令与智能卡相结合的认证方式仍存在一定安全风险。
随着将稳定的、关联度大且便于提取的生物特征作为认证要素的生物认证技术的蓬勃发展[8,11-15],关于结合了生物特征、口令以及智能卡的三因子远程认证协议的研究越来越多,应用也更为广泛。
2014年,Chuang 等[16]提出了一种仅利用hash 函数的匿名的三因子认证协议,但被Mishra 等[17]指出存在无法抵抗智能卡丢失攻击和假冒攻击等安全问题,且匿名性不够完善;2016年,王瑞兵等[18]提出了一种新的匿名认证协议,并声称能够抵抗各种攻击;2017 年,刘鑫玥等[14]指出文献[18]中的协议不能抵御恶意服务器攻击、平行会话攻击和重放攻击,提出了一个更安全的协议,但却失去了匿名性;此外,Chaudhry 等[19]提出了将椭圆曲线与生物特征相结合,并在效率上作出一定改进的协议。但夏鹏真等[20]指出文献[19]中的协议存在无法抵抗假冒攻击等问题,同时提出了优化方案;2018 年,殷秋实等[21]分析了文献[20]中的协议所存在的安全性问题,并在其基础上提出了一个更高效的协议,但无法避免口令猜测攻击;2019 年,杜浩瑞等[22]基于RSA(Rivest-Shamir-Adleman)算法设计了改进的三因子认证协议。
鉴于上述协议存在的潜在攻击与安全漏洞,本文尝试设计一种新的三因子匿名认证与密钥协商协议,便于进行双方认证,并增加口令与生物特征更新阶段以及智能卡更新分配阶段。通过合理地利用椭圆曲线上的计算性Diffie-Hellman(Computational Diffie-Hellman,CDH)假设[8],在随机预言机模型下证明了所提协议具有前向安全性、抗重放攻击、抗已知密钥攻击、抗口令猜测攻击、抵抗内部攻击、抗生物特征丢失攻击、抗智能卡丢失攻击、抗中间人攻击、抗平行会话攻击等安全性质。最后,对协议进行了安全性和计算效率分析,相较于部分现有协议,所提协议具有良好的安全属性以及较高的通信效率与实用性,且满足客户匿名性、客户口令自由更新等属性。
1 背景知识
1.1 椭圆曲线上的CDH假设
对于以椭圆曲线E上的点P为生成元所构成的q阶循环群G,以及任意未知 的a,b∈(q为一大素数),已知P,aP,bP∈G,任意多项式时间内的敌手均无法以不可忽略的概率计算出abP。
1.2 安全模型
本文基于随机预言机模型,结合智能卡与生物特征进行了安全性的形式化分析,模型包含合法客户C、服务提供方S与可控制通信信道的敌手A。每个合法客户都拥有其唯一的智能卡、口令与生物特征。敌手通过对客户与服务提供方之间的协议会话实例进行查询,进而试图获取会话密钥,具体模型如下:


1.3 符号说明
本文主要使用的符号的含义如表1所示。

表1 主要符号说明Tab.1 Description of main symbols
2 匿名认证与密钥协商协议
匿名认证与密钥协商协议(协议Q)包括初始化、注册、认证协商、口令与生物特征更新以及智能卡更新分配这5 个阶段,其中所涉及的部分符号含义见表1。
2.1 初始化阶段
S定义q阶循环群G和一个安全且抗碰撞的单向hash 函数H:{0,1}∗→{0,1}l,随机选取私钥s∈,并计算公钥P0=sP。
2.2 注册阶段
注册阶段的流程如图1所示,具体步骤如下:


图1 注册阶段Fig.1 Registration phase
2.3 认证协商阶段
认证协商阶段的流程如图2所示,具体步骤如下:


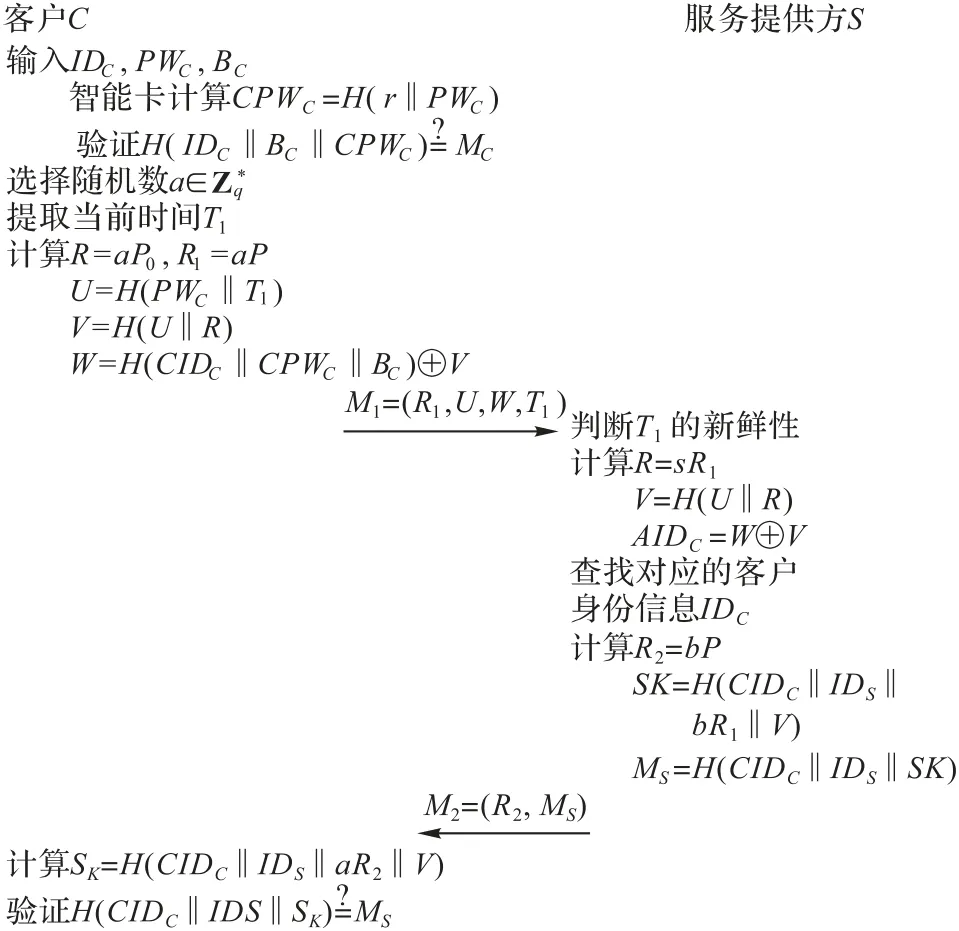
图2 认证协商阶段Fig.2 Authentication and agreement phase
2.4 口令与生物特征更新阶段
在口令和生物特征更新阶段,合法客户可以在不与服务提供方通信的情况下改变其口令和生物特征。具体步骤如下:


2.5 智能卡的更新分配阶段
本文协议中,合法客户C有权在智能卡中增添认证所需信息。

客户C收到智能卡后再次秘密保存新的随机数rˉ于智能卡中,至此,智能卡完成一次更新分配。
3 协议分析
3.1 协议的安全性证明
定理1若H:{0,1}∗→{0,1}l为随机预言机,在椭圆曲线上的CDH 假设成立的条件下,本文所提协议Q 满足安全模型中的AKA 安全定义。进一步说,假设客户C的口令空间大小为|N|,敌手A在概率多项式时间t内最多进行qE次Execute查询、qSend次Send查询、qH次H(·)查询、qj次会话,则有:

证明 模拟器T用于模拟运行协议Q 并回答敌手A的询问,协议的安全性证明通过T与A之间的一系列游戏完成[1]。定义从G0到G3的4 个游戏,并以Succi表示A成功区分Gi中Test 查询所返回的数是随机数或真实的会话密钥这一事件,下面进行具体证明。
1)游戏G0。真实的游戏,由语义安全的定义可知:
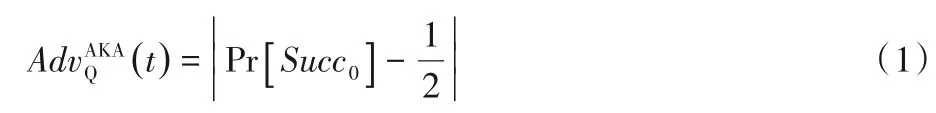
2)游戏G1。T模拟运行协议,维护初始为空的列表LH用来保存对预言机的询问以及回答。易知,在随机预言机模型下G1与G0不可区分,即有:

3)游戏G2。T仍如游戏G1中一样模拟运行协议,只是排除hash 函数之间的碰撞以及不同协议实例之间选取相同参数运行协议所发生的碰撞。利用生日悖论进行约束,可得:

4)游戏G3。假设服务提供方S不可攻陷,即私钥s仅S可知,则依据本文协议,客户C的口令也仅自己可知,依据抗碰撞的单向hash 函数的性质,即便CPWC在认证协商过程中被敌手截获,A仍难以获得PWC。因此,A只能在客户生物特征信息未知或已知的情况下尝试获取会话密钥。
情况1 客户生物特征信息未知。在此情况下,T依照安全模型模拟协议运行并回答敌手A的相关查询。具体过程如下:
1)T进行初始化,从qj个会话中任选一个作为测试会话,并嵌入CDH 二元组(xP,yP)到测试会话中,以xP和yP代替测试会话中的公钥P0和共享秘密R1。若A能以不可忽略的优势正确猜测出测试会话所返回的b′,则T可利用A求出xyP来破解椭圆曲线上的CDH问题。
2)对于非测试会话,无论A进行何种查询,T均可正确地模拟协议运行。
①当A选择会话进行Execute()或Send(,M1)查询时,因S的私钥未知,故无法直接计算共享秘密R以及临时密钥V进行回答。此时,T先检查是否存在(U,∗,H(U‖∗))∈LH。若存在,则令H(U‖∗)作为V的值,依照协议运行并返回M2给A;若不存在,T选取随机数h∈,再令h=H(U‖⊥)作为V的值模拟协议运行,并存储该H(·)查询及其应答h于LH。
②若A冒充S对C的协议实例进行Execute(ΠnS)或Send(,M2)查询,则T可采取同样方式进行回答,从而可得V并正确模拟协议运行。
③当A进行Reveal查询时,若协议已获得会话密钥SK,T直接返回相应的值;若协议未获得会话密钥SK,T返回⊥。
3)对于测试会话,当A选择测试会话进行Test查询时,T仍可按协议运行得出实例,只是在回答C的Test 查询时,返回随机数作为会话密钥。此时,若A能确定返回的值是真实的会话密钥或随机数,则其必已获得真实的会话密钥SK=H(CIDC‖IDS‖abP‖V),即A进行了相应的H(·)查询,则T便可查看hash 列表LH得到对应的V=H(U‖xyP),从而可以再次查询获得xyP,也就解决了椭圆曲线上的CDH问题。
设A正好选择T选择的会话作为测试会话,并以相应会话作为测试会话的匹配会话,则此概率为。因此,在情况1中A破解协议Q的AKA安全性质的概率可被限定为:
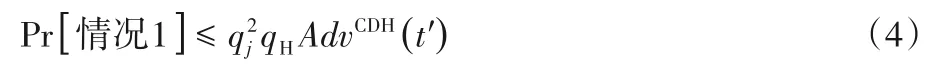
情况2 客户生物特征已知。在此情况下,A对C进行了Biometric Reveal(IDC,BC)查询,获得了生物特征信息BC。
a)若A从口令空间中选取PWC′作为C的真实口令在线与S进行交互。此时,若A正确地猜测出IDC与PWC并通过查询伪装成客户C进行认证,则可计算出真实的会话密钥并破解协议Q的AKA安全性质,其概率可被限定为:

b)若A通过H(·)查询与Smartcard Reveal()IDC,smart card查询分别获得W与智能卡信息MC、r,并通过验证正确猜测出IDC与PWC,则A必定可以计算出V,从而T可以通过查询获得xyP,进而解决椭圆曲线上的CDH 问题。此时,A破解协议Q的AKA安全性质的概率被限定为:
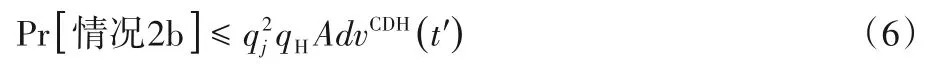
由上述分析可得,除非破解CDH 问题,否则游戏G3与G2不可区分。因此:
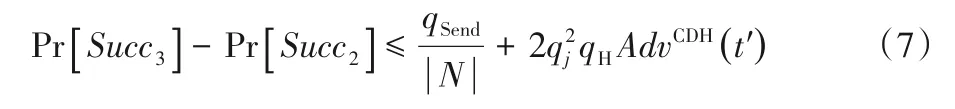
此外,对于所有消息均随机的协议,敌手没有通过信息交互便成功猜测出测试会话所返回的数是真实会话密钥还是随机数的概率为:

因此,综合式(2)、(3)、(7)、(8),A破解协议Q 的AKA 安全性质的概率为:

因椭圆曲线上的CDH 假设成立,即有AdvCDH(t′)可忽略。故由安全模型中的定义3可知,本文所提协议是语义安全的。证毕。
下面,本文对服务提供方S可被攻陷的情况进行安全性分析:
1)S被攻陷后,A将获得其长期私钥s。由会话密钥SK=H(CIDC‖IDS‖abP‖V)的构成可知,此时A能计算出V,但不能计算出每次会话都更新的密钥协商值abP,故A仍需解决椭圆曲线上的CDH 问题。由此可得,A无法获得已结束的会话密钥,从而说明已结束的会话仍是安全的,协议具有前向安全性。
2)由抗碰撞的单向hash 函数的性质可知,即使S被攻陷,A也难以获得PWC,即保证了客户口令安全。
3.2 协议的性能分析
从计算消耗和安全性两方面对所提协议性能进行分析:
1)计算消耗方面。
主要针对认证密钥协商阶段同文献[8,21-22]中的三因子认证与密钥协商协议进行比较,为了使对比结果更准确,首先定义了一些符号及其单次计算时间,具体如表2 所示,此时间数据来自文献[25]。
由表3 可知,本文协议与文献[8]中的协议相比,未使用MAC(Message Authentication Codes)算 法(MAC:{0,1}l×{0,1}∗→{0,1}l上的函数,即输入密钥k∈{0,1}l与任意长的待认证的消息m∈{0,1}∗,输出t=MACk(m)),服务提供方也减少了一次hash函数的运算,故计算量相对较低;结合表2的单次计算时间可知,本文协议的计算耗时和文献[21]协议相近,比文献[22]协议少。此外,考虑信息交互次数,即通信开销方面,本文协议也具有一定优势。

表2 符号定义及其单次计算时间Tab.2 Symbol definition and its single calculation time
忽略不计轻量级⊕、‖运算,则对比结果如表3所示。

表3 不同协议计算性能对比Tab.3 Computational performance comparison of different protocols
2)安全性方面。
首先,说明认证与密钥协商协议在安全性方面所应具备的一些安全属性(双向认证、安全的密钥协商、抗中间人攻击、抗重放攻击、抗已知密钥攻击、抗平行会话攻击、抗智能卡丢失攻击、抗生物特征丢失攻击、抗口令猜测攻击、前向安全性)已包含在本文所提出的安全模型当中,也即:在该模型下证明满足安全性定义的协议具有上述安全属性[26]。
其次,由于客户可以申请对智能卡进行更新分配,故协议Q可以抵抗内部攻击;由对服务提供方S被攻陷的情况的安全性分析可知,协议Q可抵御恶意服务器攻击,同时保证了口令安全;由口令与生物特征更新阶段的设定可知,协议Q具有口令自由更新的属性。
此外,由于公开信道上交互的信息均以随机化匿名信息CIDC代替客户的明文信息IDC,故由抗碰撞的单向hash 函数的性质可知,即使A获得了智能卡信息也无法求得IDC。在C与S的认证过程中,S需利用私钥s,通过一系列计算,才能从数据库中检索出对应客户,进而找到IDC,这有效地保护了客户的匿名性与隐私性。
通过证明分析可得,相应的对比结果如表4所示。

表4 不同协议安全性能对比Tab.4 Safety performance comparison of different protocols
文献[8]协议未设置口令更新修改阶段,故不具有口令自由更新的属性,且协议中客户的身份标识IDU是在公共信道中明文传输的,因此可被敌手截获传输中的消息并得知客户身份,无法保证匿名性;由文献[27]可知,文献[21]协议无法避免口令猜测攻击;文献[22]协议中客户也可对智能卡信息进行修改,但未设置智能卡丢失后的更新阶段,因而敌手可以窃取智能卡,并篡改认证所需的随机数信息,在这样的修改下,口令更改阶段也自然无法与前面的登录认证阶段相对应,根本无法按照设定步骤执行,故口令无法得到自由更新。因而,相比之下,本文协议拥有更强的安全性,在功能性方面也更加实用。
综合上述分析可得,本文协议相较对比协议不仅在安全性能方面有所提升,也在计算性能方面具有一定优势。
4 结语
通过对三因子认证与密钥协商的相关研究工作进行分析,为解决常见的安全问题,结合智能卡与口令、生物认证技术等方法,本文设计了一种三因子匿名认证与密钥协商协议,并在随机预言机模型下基于椭圆曲线上的CDH 假设对协议的安全性进行了证明。综合性能分析表明,本文协议不仅具有较高的计算效率与通信效率,还提升了认证协商过程的安全性,在信息管理等领域具有应用可靠性。
此外,由于传统的时间戳技术在界定时限方面受较多因素影响,故方案的局限性在于可能要求应用设备具有较强的处理能力。如何在满足基本安全特性的前提下进一步降低协议的空间和时间复杂度,并考虑将所提协议应用到更多环境,例如物联网、云计算等是进一步仍待研究的问题。

