掌握规律，得心应手

卢日荣

摘要：折叠题型就是把一个几何图形的一部分沿某一条直线或线段折叠，通过这部分图形折叠变换前后相等的等量关系来命题。试题综合考查了学生的观察能力，空间想象能力和动手能力。其形式多样，变幻巧妙，立意新颖，综合性强。因此这类题型是历年各省市中数学考中的热点题型，也是学生失分最严重的题型。为了使学生在这类题中不丢分，我们老师在数学中考备考中应认真专研这类考题特点，弄清命题结构和规律，在平时的训练中应培养学生的识图能力、观察能力及解决问题的能力。

关键词：折叠;折法;策略

在复习折叠问题时，教师应归纳出这类题型的特征、考察形式以及有关的解题规律，总结出相关对策、解法并找到与此相关的一类题。下面本人结合实际教学，谈谈自己在复习折叠问题时的一些做法。

一、紧扣课本，梳理考点

通过学生的动手操作，让学生比较直观认识和理解几何图形的折叠变换的概念和特性。

1.几何图形折叠的概念

几何图形折叠就是把一个几何图形的一部分沿某一条线段或直线折叠，使它与原图形的另一部分重叠或者不重叠。

2.几何图形折叠的特性

（1）几何图形的折叠部分前和后都是全等形。

（2）几何图形的折叠部分所在折叠前和折叠后的位置，关于折痕成轴对称。

例1（石家庄市）如图1，在矩形ABCD的纸片中，要在矩形ABCD的纸片里折出一个最大的正方形。有同学把矩形的一个∠B沿线段AE向上折叠，使AB与AD边上的AF重合，则四边形ABEF就是一个最大的正方形。这位同学说四边形ABEF是一个最大正方形，根据什么来判定呢？

分析：这位同学把矩形的一个∠B线段AE向上折叠，使AB和AD边上的AF重合，根据折叠的性质，很容易得到： ，对角线平分内角的矩形是正方形，因此四边形ABEF在矩形ABCD里就是一个最大的正方形。

二、回归课本，掌握折法

在各省市数学中考有关折叠题目中，有很多是源于课本的。命题者通过课本的例题、习题进行“二次开发”，变成一道新的考试题目。对这类紧扣课本试题，我们在数学中考复习中一定要注意对课本有关折叠知识的研究与挖掘，得出解题规律，化繁为简，达到灵活变通、触类旁通的目

的。下面以初中数学人教版教材中的两道题目为例，弄清在折叠中对直角三角形和矩形是怎样折的问题。

例2（人教版八年级上册第58页第14题）如图2，在直角三角形ABC中，若∠C=90°∠B=30°，要把这个直角三角形均匀分成三个面积相等的直角三角形，你有办法吗？请你试着在图上画出来，并说明原因。

解：作∠A的平分线AD交BC于D，过D作DE⊥AB于E，得到3个全等三角形。

∵∠C=90°∠B=30°

∴∠CAB=60°

∵AD为∠BAC的角平分线

∴∠BAD=∠CAD= ∠CAB=30°

∴AC=  CD，且S△ACD= AC·CD

∵∠DAE=30°且∠DEA=90°

∴AD=2DE

∴DE=CD可证△ACD≌△AED

同理△ACD≌△BED

S△ADE= AE·DE=S△BDE= BE·DE=S△ACD

通过分析很容易得出此类题解题方法如图3所示沿∠CAB的角平分线AD和边AB的垂直平分线，DE划分即可。此题看似与折叠问题无关，但它实际包含了直角三角形的几种常见的折叠类型，归纳如下：

1、沿一個锐角的角平分线折叠，如图4;

2、沿斜边的垂直平分线折叠，如图5;

3、沿一条直角边的垂直平分线折叠，如图6;

变式训练：

1、图2中，若AC=3，BC=4求线段CD的长

2、图3中，若AC=3，BC=4求线段CD的长

3、图4中，若AC=3，BC=4求线段CE的长

规律总结：利用折叠的性质得到的直角和相等的边或角，选择适当的直角三角形，运用勾股定理列方程或利用直角三角函数，是解决这类问题的关键。

例3（人教版八年级上册第53页练习2）四边形ABCD是矩形，△BCD沿矩形对角线BD向上折叠，如图7重叠部分△BFD是一个等腰三角形吗？为什么？

此题是矩形折叠后的有关三角形证明，解决矩形的折叠问题，实际上是把它转化为三角形的问题去解决。矩形折叠与三角形折叠相比较，矩形折叠中的条件更丰富，融入了矩形的性质的运用，因而它比三角形的折叠更复杂，常以此题基础变式出了许多的中考题型。如2018年广东中考题数学第22题。

规律总结：矩形常见的折叠规律

（1）如图8，沿矩形ABCD的对角线BD折叠。

（2）如图9，沿矩形ABCD的对角线BD折叠。

（3）如图10，△BCE沿直线CE向上折叠，点B落在线段AD点F上。

变式训练：

（1）图8中，若AB=3，BC=4求线段AF的长

（2）图9中，若AB=3，BC=4求线段AF的长

（3）图10中，若AC=3，BC=5求线段AF的长

规律总结：首先要抓住矩形折叠的本质特点，找出折叠前后相等的边和角，再把矩形折叠问题转化为直角三角形问题，找出关键的直角三角形，运用勾股定理列方程或解直角三角形来解决这类问题。

三、研究中考，剖析题型

在掌握几何图形折叠的性质及折叠问题中常见的折叠法后，我们就要剖析各省市的中考中关于几何图形折叠问题的常见类型题，引导学生触类旁通，懂一题会一片。培养学生解决几何图形折叠问题的能力，真正做到胸有成竹。

1.几何图形折叠后求角度

例4（2016.长沙市）在一般△ABC中。

（1）如图②所示，点A向下沿DE折叠，使点A落在四边形BCED的内部点A′的位置，∠1、∠2与∠A之间存在怎样的数量关系？为什么？

（2）如图①，点A向下沿DE折叠，点A刚好落在边AC上的点A′的位置，∠A与∠1存在怎样的数量关系？为什么？

（3）如图③，点A向下沿DE折叠，使点A落在四边形BCED的外部点A′的位置，∠A、∠1与∠2之间存在怎样的数量关系？为什么？

解：（1）∵如图②点A折叠后落在点A′的位置，点A′在四边形BCED内

∴∠ADE=∠A′DE∠AED=∠A′ED

∴∠ADE=12（180°-∠1）∠AED=12（180°-∠2）

在△ADE中，∠A+∠ADE+∠AED=180°

∴∠A+12（180°-∠1）+12（180°-∠2）=180°

整理得，2∠A=∠1+∠2

（2）如图①∵点A折叠后落在点A′的位置，点A′在线段上，

∴∠A=∠DA′E

由三角形外角性质得：∠1=∠A+∠DA′E=2∠DA′E=2∠A

（3）如图③，∵点A折叠后落在点A′的位置，点A′在四边形BCED外

∴∠A=∠A′由三角形的外角性质得：∠3=∠2+∠A′∠1=∠A+∠3

∴∠1=∠A+∠2+∠A′=∠2+2∠A

即∠1=∠2+2∠A.

经验总结：如果几何图形只有一次折叠，我们只要抓住几何图形折叠的性质，利用折叠前后两个三角形是全等型这一本质特征，就可以解决问题。对于几次折叠的问题可通过操作相结合的方法解决。

2.几何图形折叠后求线段长度

例5（济南市2000年中考试题）

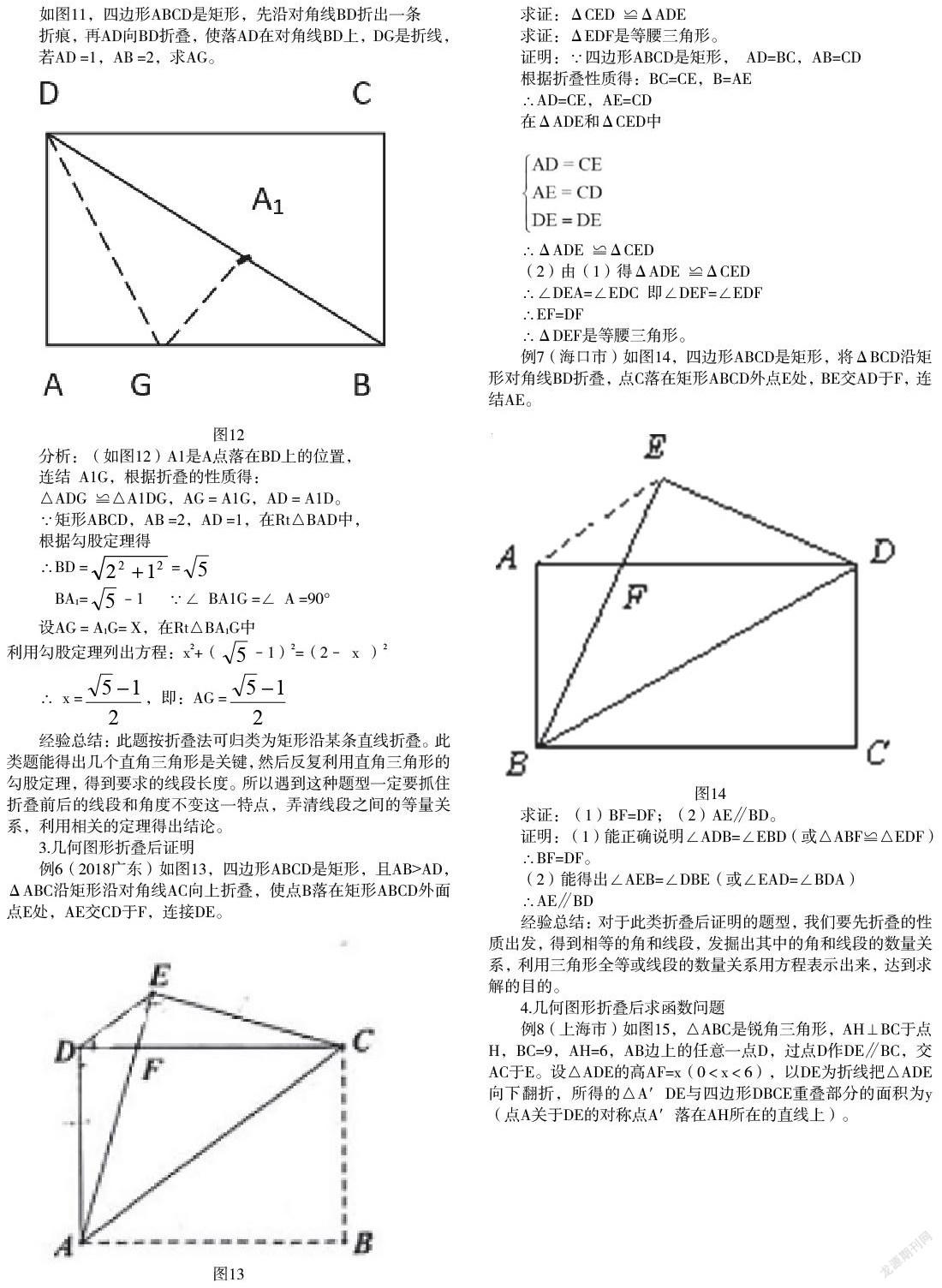
如图11，四边形ABCD是矩形，先沿对角线BD折出一条

折痕，再AD向BD折叠，使落AD在对角线BD上，DG是折线，

若AD =1，AB =2，求AG。

分析：（如图12）A1是A点落在BD上的位置，

连结 A1G，根据折叠的性质得：

△ADG ≌△A1DG，AG = A1G，AD = A1D。

∵矩形ABCD，AB =2，AD =1，在Rt△BAD中，

根据勾股定理得

∴BD = =

BA1= –1∵∠ BA1G =∠ A =90°

设AG = A1G= X，在Rt△BA1G中

利用勾股定理列出方程：x2+（ –1）2=（2– x ）2

∴ x = ，即：AG =

经验总结：此题按折叠法可归类为矩形沿某条直线折叠。此类题能得出几个直角三角形是关键，然后反复利用直角三角形的勾股定理，得到要求的线段长度。所以遇到这种题型一定要抓住折叠前后的线段和角度不变这一特点，弄清线段之间的等量关系，利用相关的定理得出结论。

3.几何图形折叠后证明

例6（2018广东）如图13，四边形ABCD是矩形，且AB˃AD，ΔABC沿矩形沿对角线AC向上折叠，使点B落在矩形ABCD外面点E处，AE交CD于F，连接DE。

求证：ΔCED ≌ΔADE

求证：ΔEDF是等腰三角形。

证明：∵四边形ABCD是矩形， AD=BC，AB=CD

根据折叠性质得：BC=CE，B=AE

∴AD=CE，AE=CD

在ΔADE和ΔCED中

∴ΔADE ≌ΔCED

（2）由（1）得ΔADE ≌ΔCED

∴∠DEA=∠EDC 即∠DEF=∠EDF

∴EF=DF

∴ΔDEF是等腰三角形。

例7（海口市）如图14，四边形ABCD是矩形，将ΔBCD沿矩形对角线BD折叠，点C落在矩形ABCD外点E处，BE交AD于F，连结AE。

求证：（1）BF=DF;（2）AE∥BD。

证明：（1）能正确说明∠ADB=∠EBD（或△ABF≌△EDF）

∴BF=DF。

（2）能得出∠AEB=∠DBE（或∠EAD=∠BDA）

∴AE∥BD

经验总结：对于此类折叠后证明的题型，我们要先折叠的性质出发，得到相等的角和线段，发掘出其中的角和线段的数量关系，利用三角形全等或线段的数量关系用方程表示出來，达到求解的目的。

4.几何图形折叠后求函数问题

例8（上海市）如图15，△ABC是锐角三角形，AH⊥BC于点H，BC=9，AH=6，AB边上的任意一点D，过点D作DE∥BC，交AC于E。设△ADE的高AF=x（0

（1）①求出当0

（2）当x取什么值时，y的值最大或最小值？是多少？

解：（1）①当0

∵DE∥BC

∴∠ADE=∠B，∠AED=∠C

∴△ADE∽△ABC

∴ .∴ ，即

又∵FA'=FA=x

∴y= DE·A'F= · x·x

∴ （0

②当3

∵FH=6-AF=6-x

A'H=A'F-FH=x-（6-x）=2x-6

又∵DE∥PQ

∴△A'PQ∽△A'DE

∴

∴

∴

（2）当0

当3

∵y1

经验总结：此题考察了几何折叠问题与动点函数问题。利用几何图形折叠的性质、相似三角形的性质和二次函数的性质。求出函数的最大值最小值。解决此类题的关键是熟练掌握相似三角形的性质，找出线段的等量关系，也就是函数关系，从而快速求解。

几何图形的折叠问题是数学中考的热点、难点题型。此类题型综合考察学生的空间想能力和知识的综合运用能力。在平时的复习训练中，要培养学生数形结合的思想与综合运用能力。虽然此类题型变化之多，考察范围之广，但是经过深入研究之后，我们不难发现其中的命题规律，在解决此类题型，我们要教会学生细心观察，利用几何图形折叠的性质，发现问题所在，化繁为简，才能轻车熟路，得心应手。

参考文献：

[1]甘晓云.图形折叠与变换[J].学苑创造：C版，2018（4）：4-4.

[2]朱晓勤.矩形折叠问题的深度探析[J].文理导航，2018（20）：1-1.

[3]肖学仕.巧解初中几何折叠问题[J].数理化解题研究：初中版，2014（9）：1-1.

[4]李殿起.折叠图形问题的解法[J].初中生之友，2003（Z5）：37-39.