基于支持向量机模型的地表下沉系数计算参数寻优

熊睿

(江西铜业集团东同矿业有限责任公司， 江西 抚州市 331800)

矿石一般埋于地表以下，开采矿石会引起地表沉降，给安全生产带来隐患。充填采矿法具有较低的贫化率和较高的回采率，能够充分利用现有资源，并且能够在一定范围内控制地表的沉陷及控制地压等[1]，所以充填采矿法在工程中的使用较为普遍[2]。为了科学合理地评价充填效果，有必要对地表下沉系数进行快速准确的预测，为下一步的合理施工提供科学依据，特别是地表存在重要的基础设施或文物保护时，地表下沉系数的预测尤为重要。影响地表下沉的原因很多，各个因素与下沉系数之间的关系不是简单的线性关系[3]。目前较为常见的地表下沉系数计算方法包括神经网络、概率积分、数值模拟等[3-10]。而其中使用较普遍的是神经网络模型，虽然预测精度较高，但是需要大量的测试数据才能保证预测的准确率，而且容易陷入局部极小点。而与神经网络类似的SVM，其训练模式采用优化技术及数学方式，因而在处理小样本、非线性数据领域具有较强优势[11-14]，可以避免前者的结构选择和局部极小点的问题。因此，本文通过3种寻优算法，包括网格参数、GA、PSO来优化参数，建立更合适的SVM模型，并类比分析采用以上方法所得到的不同参数值，评估其预测结果的准确性，确定最适合地表下沉系数预测的SVM回归模型。同时，本文考虑了交叉概率对支持向量机模型预测性能影响[15]，采用改进的 GA-SVM 模型对地表下沉系数进行预测，并与PSO-SVM、传统GA-SVM、网格寻优算法结果进行比较，以期选择更为合适的SVM寻优算法。

1 SVM模型的参数寻优算法

SVM是构建在统计学习理论的VC维理论和结构风险最小的框架上，基于有限的样本信息，既要提高训练样本的学习精度，又要在无错误地识别任意样本的本领之间保持平衡，以期获得最好的推广能力。

核函数当中的系数c及参数g对SVM模型机能改变较大，因而有必要通过特定算法来选取最优数值。当前常用的优化法包括网格参数、GA、PSO。其流程如图1～图3所示[15]。

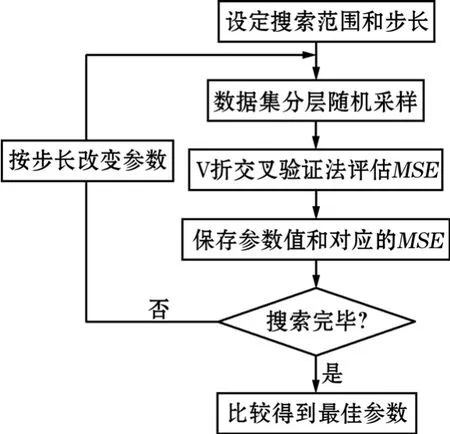
图1 网格参数寻优算法流程

图2 GA算法流程

图3 PSO算法流程

样本数据来至文献[3]的表1数据。与文献[3]一致，第1～34组的数据作为训练数集，第35～40组的数据作为检验数集。通过上诉3种寻优方式对SVM模型参数c和g进行优化求解，得到3种不同的c和g值，见图4～图6。由图4～图6可知，GA算法、PSO算法、网格参数寻优算法计算得到的c和g分别为67.4424，12.8566；79.2548，0.7809；8，0.1250，3种算法得到的c、g值差别较大。GA算法的均方误差δMSE值最小，PSO算法次之；PSO算法与网格参数寻优算法的结果相差不大。

图4 网格参数寻优算法结果

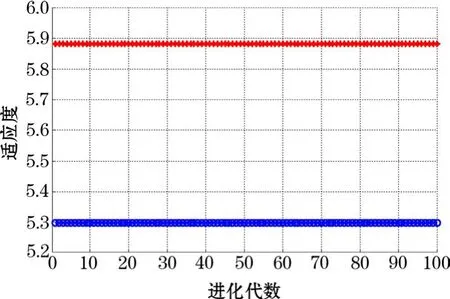
图5 GA 参数寻优算法结果

图6 PSO参数寻优算法结果

2 3种算法结果的验证

分别采用以上3种算法优化的c和g值构建各自的SVM模型，使用3种模型分别对样本空间的训练样本和测试样本进行回归预测。图7～图9为不同寻优算法的回归预测结果。

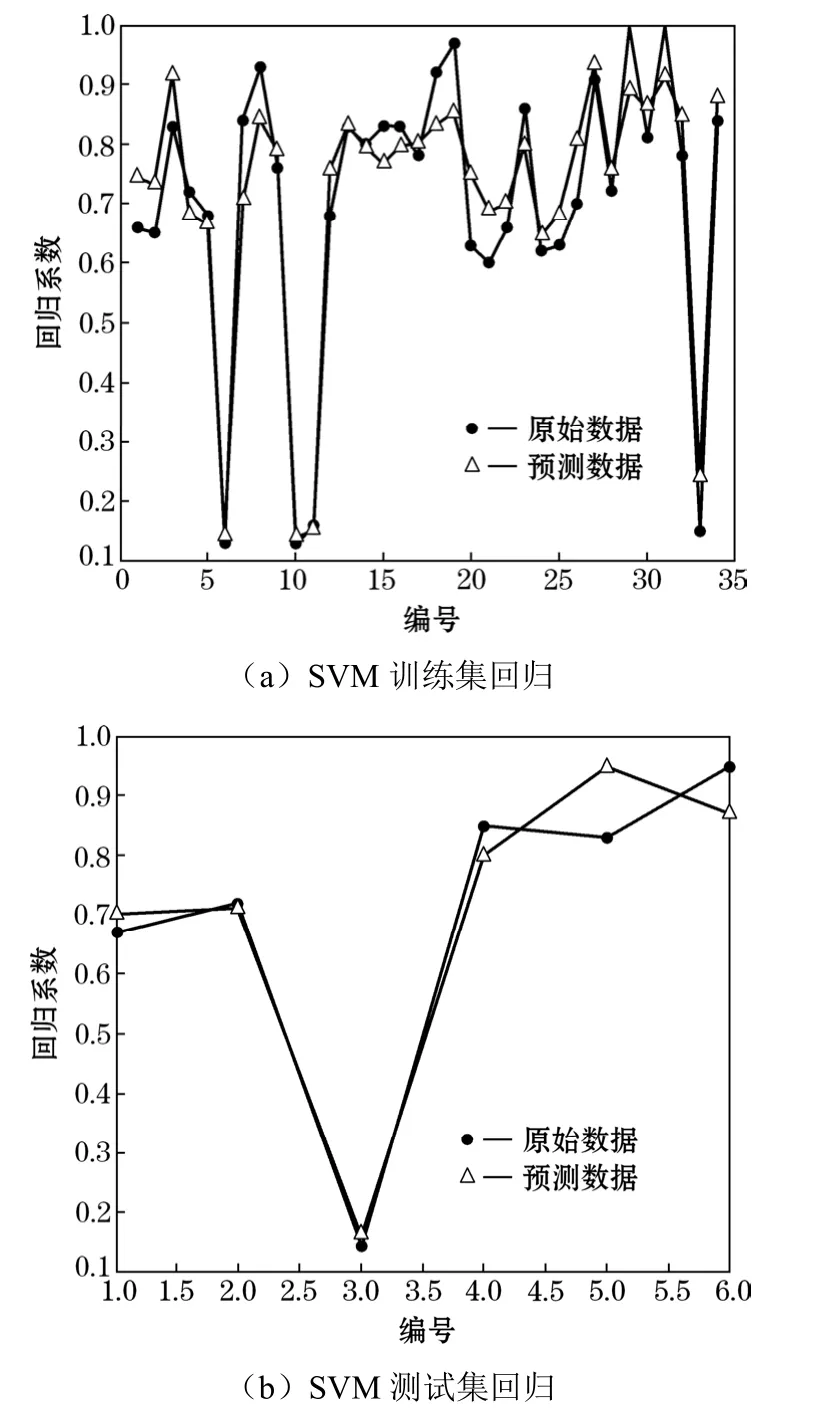
图7 网格参数寻优算法验证结果

图8 GA寻优算法验证结果

图9 PSO寻优算法验证结果

从图7～图9可看出，GA算法、PSO算法、网格参数寻优算法获得的SVM模型在训练集上的回归系数分别为 0.95472，0.93528，0.91515，说明GA算法的回归效果最好。网格参数寻优算法、PSO算法的测试集回归系数分别为0.94253，0.91604，反映了网格参数寻优的推广性较强。而GA算法的测试样本回归系数最差，说明其泛化能力较差。文献[15]认为 SVM 模型的性能会受到交叉概率的影响，为了提高GA算法预测性能，采用基于交叉概率寻优的GA算法对SVM模型的c、g进行寻优，结果见图10。同样，采用改进后的GA模型对训练样本及预测样本进行回归预测（见图11）。由图11可知，基于交叉概率的GA算法可以改善模型的预测准确度，回归系数为0.95271。其测试集回归系数较未考虑交叉概率大，说明考虑交叉概率的GA算法具有很强的泛化能力，最优参数c为63.6334，g为0.030232，交叉概率p为0.1511。

图10 改进的GA参数寻优算法结果

图11 改进的GA寻优算法结果

3 结论

本文通过对我国典型地表移动观测站实际案例建立SVM机模型，采用了不同的算法对模型相关参数进行寻优，并基于最优参数对地表下沉系数进行预测，得出改进的GA算法考虑了交叉概率对预测性能的影响，更适合地表下沉系数预测分析。该算法的预测回归系数最高，可以达到0.95271，网格参数寻优及 PSO算法的预测回归系数分别达到0.94253和0.91604；SVM模型在预测地表下沉系数的应用中具有可行性，特别是在地表沉降案例较少的情况下，即不需要大量的地表沉降数据进行模型的训练。影响地表下沉系数的因素较为复杂，本文为计算方便进行了简化，建立的支持向量机模型尚不完善，但为地表下沉系数的快速预测分析提供了新的方法。