激光点云中典型地物分割方法

邹纪伟, 刘德儿, 康 翔, 兰小机, 杨 鹏, 刘靖钰

(江西理工大学 土木与测绘工程学院, 江西 赣州 341000)

0 引 言

三维激光扫描技术自问世以来已被应用于各个领域, 如文物修复、建筑物的三维建模、智慧城市的建设和大面积的地形测量等[1]。地面激光扫描仪能够快速高精度地获取地物的表面信息, 相比于机载激光扫描仪和航空摄影测量, 其获取的数据更加精细[2], 由于点云数据量庞大, 若直接对其进行操作, 工作量较大且耗时长, 因此需对源数据进一步处理, 点云分割作为数据处理的关键环节, 其分割精度直接影响到后续点云三维重建、特征提取、地物识别等操作。

常见的点云分割算法有RANSAC算法、欧氏聚类算法、区域增长算法、最小割算法等。RANSAC算法作为随机参数的估计算法[3], 由Fishier等于1981年提出, 该算法在直线拟合、平面拟合、计算图形方面应用广泛, 在点云分割中, 该算法通常用于提取平面点云：李娜等[4]将RANSAC算法运用于点云的分割处理, 提取出了建筑物的特征立面；贺亦峰等[5]则通过设置不同阈值, 使用RANSAC算法将建筑立面中的墙面、窗户、阳台等要素单独分割开来, 再通过欧氏聚类完成独立个体的分割。基于欧氏聚类的点云分割是根据不同点间的欧氏距离来判断是否属于同类地物点：吴燕雄等[6]使用欧氏聚类加上平滑阈值的方法对地物实现分类提取, 能够高效快速地达到分割效果, 但若地物种类过多, 阈值则较难设置, 易出现过分割或欠分割现象。区域增长算法[7-10]则是根据法向量及曲率实现不同地物分割：王竞雪等[11]提出了一种对机载LiDAR数据中的建筑物提取, 通过区域生长算法与主成分分析相结合的方法实现高精度提取；李仁忠等[12]提出了通过将估算的曲率最小点设置为种子点的改进区域生长算法, 使分割的精确性及可靠性得到提高；孙金虎等[13]提出了基于最小生成树(MST)改进的区域生长算法, 能够得到平滑的分割边界。

上述常见的点云分割算法, 若单独应用于大型室外场景点云, 都存在一定的局限性, RANSAC算法适用于建筑立面细节特征的分割提取, 倘若建筑物结构较为复杂, 则需设置不同的平面模型参数进行分割, 操作较为繁琐。欧氏聚类算法适用于相距较远的不同地物点云分割, 若不同地物点云出现粘连问题, 则很难将其单独分割开, 阈值设置恰当与否, 直接影响点云分割效果。区域增长算法因其根据法向量及曲率对散乱点云进行分类, 因此对树、杆状物分割效果良好。针对激光点云中的典型地物, 找到合适的融合分割算法对其进行分割, 将有效解决过分割或欠分割问题。

综上, 本文提出基于区域增长与欧氏聚类相结合的点云分割算法：首先对数据预处理, 完成噪点去除及数据精简, 采用渐近式形态学滤波去除地面点, 再通过区域增长算法将树、杆状物和建筑类地物单独分割开, 最后用欧氏聚类实现对典型地物的有效分割, 解决传统点云分割算法易出现过分割或欠分割问题, 为后续点云数据处理提供基础。

1 数据预处理

通过地面激光扫描仪采集到的数据由于受环境因素的影响, 不可避免地产生噪声, 影响后续实验的分割效果, 因此本文在分割前先对源数据进行去噪处理。具体地，统计滤波通过对每个点的邻域进行统计分析, 计算该点至其邻域点的平均距离, 得到高斯分布图, 将平均距离到标准范围之外的点定义为离群点, 使用时仅需设置K近邻搜索个数和标准差倍数就可将噪声点从数据中去除。本文采集数据的噪声符合这一特性, 因此采用该算法对噪声点进行有效移除。经滤波后, 由于数据仍然过密, 影响后续分割算法的运行效率, 在保证数据特征信息的前提下, 采用八叉树对数据进行精简。该算法首先对点云创建一个八叉树, 在树中搜索并记录真实的叶节点数据, 然后将节点数和对应的数据作为平均聚类算法K值和初始聚类中心, 最终计算出每个点的均方根曲率、所有点的均方根曲率均值、每个点到聚类中心的欧氏距离以及每个点到聚类中心的欧氏距离的平均值, 根据计算结果精简点云数据。

本文实验数据通过RIEGL VZ-1000扫描仪获取, 其中源数据点个数为1 133 991, 通过对数据进行去噪及精简, 同时手动对无效点进行移除, 最终得到的结果见图1, 其中统计滤波K近邻搜索个数设置为6, 标准差倍数设置为1.0, 而精简点云细分级别设置成10, 去噪后点个数为1 115 968(图1b)，精简及手动去除无效点后点个数为109 130(图1c), 可见预处理后的点云噪点被较好地移除, 地物更加清晰, 便于分割处理, 且数据精简后将更好地提高算法的运行效率。

图1 数据预处理

2 点云分割算法

2.1 地面点移除

由于采集数据时不可避免夹杂地面点云, 为了确保点云分割的质量, 需要对该区域点云进行有效去除。本文研究数据为室外大型场景点云, 虽然地形较为平坦, 但仍夹杂地形起伏较大区域, 因而采用渐近式形态学滤波去除地面点。

形态学滤波的主要操作为腐蚀与膨胀, 该滤波算法在二维图像中运用较为广泛, 其中先腐蚀后膨胀称为开运算, 该操作可对小区域噪声进行去除, 同时可对图像进行平滑处理; 而先膨胀后腐蚀称为闭运算, 该操作对图像细小空洞有较强的修复能力。在激光点云中, 通过腐蚀运算可获得指定区域点的最小高程值, 而膨胀操作则获得该区域内点的最大高程值。借助不断增长的滤波窗口, 通过开运算操作, 渐近式形态学滤波即可实现地面点与非地面点的分离, 该滤波操作主要通过高差阈值Δhi判断[14]

(1)

其中:h0为最小高差阈值,s为研究区域的平均地形坡度,c为格网大小,hmax为最大高差阈值, 而wi为运行到i次时滤波窗口的大小。当前后格网内的高程差小于高差阈值Δhi时, 将当前格网内的点归为地面点类格网, 标记为0; 而对于大于高差阈值的, 将该格网归为非地面点类格网, 标记为1。通过遍历所有点云数据, 即可将地面点与非地面点分离开来。

2.2 基于区域增长与欧氏聚类相结合的点云分割

欧氏聚类算法是应用于测绘领域的一种重要的点云分割算法。它利用KD树搜索近邻域点, 计算邻域点到该点的欧氏距离, 将在阈值范围内的点聚为一类, 通过反复迭代, 直到没有新点加入为止。

(2)

其中:pi,qi∈Q,Q是一个点云集。具体的实现步骤为: ①对于空间中的某点p1, 利用KD树搜索找到其近邻点, 计算这n个点到p1的距离, 将距离小于阈值的点p3、p4、p5…放到点集A中, 将点集A中的点从原始点云中移除; ②依次遍历点集A中的所有点, 重复步骤①, 更新点集A; ③当A中无新点加入时, 该类聚类完成; ④新建点集B, 对剩余点执行步骤①操作; ⑤所有点都遍历完成, 运行结束。

通过欧氏聚类进行分割的效果主要由设置的距离阈值决定: 当设置的阈值过大时, 会出现过分割现象, 建筑物与周边较近的地物归为一类,当建筑物与树木及地面周边点粘连时, 无法通过欧氏聚类分割(图2a、2b); 反之, 则出现欠分割情形, 在图2c、2d中, 由于阈值设置过小, 建筑物出现缺失现象。针对此问题并结合上述分析, 本文提出基于区域增长与欧氏聚类相结合的点云分割算法。

图2 欠分割及过分割现象

区域增长算法是将点云的法向量进行比较, 将满足平滑约束条件的相邻点归为一类, 其工作原理为先利用KD树对散乱点建立拓扑关系, 计算各点平均曲率值, 再将各点按曲率值从小到大进行排序, 将曲率值最小的点设置为种子节点, 由于曲率最小的点位于平坦区域, 从该区域进行增长可以减少区域的总数, 避免重复分割, 最后将满足条件的不同地物聚为一类。

(3)

式中:Ki为曲面中点的平均曲率近邻点；n为法向量;P为该点周围无限小的区域; diam(P)为这个区域的直径;为该点的梯度算子。该算法具体的步骤如下: ①将散乱点云按照曲率值进行排序, 找到曲率最小的点, 将其设置成种子节点，②计算该种子点与邻近点的法线差值, 若小于设置的阈值, 且曲率值也小于设定的阈值, 则将该点添加到种子点集, 即归为一类; ③将通过两次检验的点从原始点云中去除; ④设置最小和最大聚类的点数; ⑤重复步骤①～③, 算法会将满足条件的不同地物聚类为一类, 并用不同的颜色加以区分; ⑥当剩余的点云数小于最小聚类点数时, 则停止工作。

在大规模场景点云中, 建筑物等地物点云的曲率变化明显要小于树木等杆状地物, 由于区域增长算法是按法线差值与曲率变化进行分割的, 可将曲率变化较大的树木及杆状地物通过该算法分割出来, 归为一类, 将剩余地物点云划分为另一类, 再分别对两类点云执行欧氏聚类分割, 最终完成对典型地物的分割, 其分割流程见图3。

图3 典型地物分割流程图

3 实验与分析

采用RIEGL VZ-1000扫描仪获取的该数据，包含建筑物、周边低矮树木、路灯、旗杆等典型地物, 地物种类较多, 场景较为复杂。实验软硬件环境:Windows 10专业版、处理器为Intel(R)Core(TM)i5-4200M CPU @2.50 GHz、内存为8 GB; 本研究的实验算法是在Microsoft Visual Studio 2017编译环境下, 结合PCL方法库编程实现。

通过预处理后, 采用渐近形态学滤波算法移除地面点, 滤波窗口设置为20 m, 坡度设置为1.0, 最小高差阈值设置为0.5 m, 最大高差阈值设置为0.8 m, 得到的结果如图4所示。滤波后, 大量地面点都得以去除, 建筑物底部点及阶梯处点未因该操作而受影响, 较好地保证了地物点的完整性。

图4 地面点去除

经形态学滤波后, 再对非地面点采用区域增长算法进行分割, 法线差值设置为0.05, 曲率阈值设置为1.0。从图5a可以看出, 由于树及杆状物曲率变化较大, 而建筑物点云分布较为平整, 因此树及杆状物聚类后呈现红色, 而其余地物颜色与该类地物颜色不同；基于此，可将树木及杆状物点云簇分为一类(图5b)；其余地物归为另一类(图5c)。接着，分别对上述两类点云簇进行欧氏聚类分割: 将典型地物个体单独分离出来, 树及杆状物距离阈值设置成1.0 m, 最小聚类簇点数为50, 最大聚类簇点数为300 000, 最终生成的聚类簇数为53个(图6)；而对于建筑物等点云簇, 其距离阈值设置为2.0 m, 最小聚类簇点云为50, 最大聚类簇点数为300 000, 最后生成的聚类簇数为7个(图7)。

图5 区域增长分割

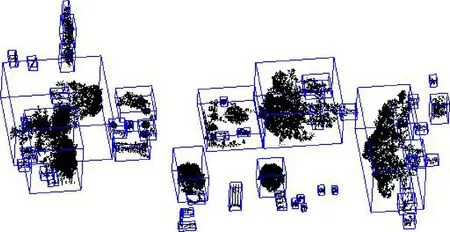
图6 树及杆状物欧氏聚类分割结果

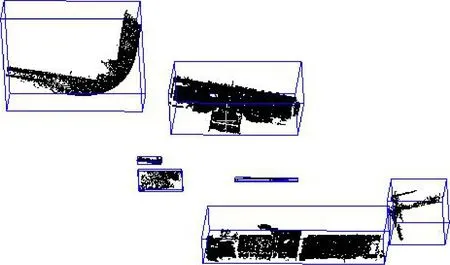
图7 建筑地物欧氏聚类结果

从图8及图9可以看出, 通过本文算法, 可将建筑物、树、旗杆等典型地物单独分割开来, 较好地解决了建筑物与地面、建筑物与树杆、树杆与地面等不同地物点云间因粘连问题而出现的过分割现象, 且本文将不同地物归为两类, 即树及杆状物点云簇和建筑物点云簇, 通过分别对其进行欧氏聚类, 较好地解决了双方对阈值设置的冲突, 避免出现地物欠分割现象。

图8 树及杆状物分割

图9 建筑物分割

4 结 论

以TLS获取的大规模场景点云数据作为研究对象, 通过统计滤波与八叉树精简对源数据作预处理, 降低了噪声点的干扰, 提高了点云分割的运行效率。由于受地物形态特征、空间位置、地面点等因素影响, 在对典型地物进行分割时，常会出现过分割或欠分割现象, 因此，本文提出基于区域增长与欧氏聚类相结合的分割算法, 首先通过形态学滤波去除地面点, 然后通过区域增长算法, 将典型地物分为树杆类及建筑物两大类, 最后分别对这两类地物通过欧氏聚类完成独立个体的有效分割。本文方法有效解决了点云分割中易出现的过分割或欠分割问题, 在对树、杆状物及建筑物等典型地物的点云分割中有较强的实用性。然而, 本文算法的阈值需要人工调试, 如何自动获取合适的阈值, 将是下阶段的研究重点, 虽然本文事先对数据作了预处理, 提高了运行效率, 但若数据量很大时, 其运行时间将成倍增长, 如何改进算法, 加入并行策略, 减少分割时间, 将是下一步的工作重点。