基于多断面水质达标的河网区点面源污染负荷优化分配模型

陈丽娜，韩龙喜，谈俊益，张防修，林囿任

(1.河海大学农业科学与工程学院，江苏 南京 210098； 2.河海大学浅水湖泊综合治理与资源开发教育部重点实验室，江苏 南京 210098； 3.河海大学环境学院，江苏 南京 210098； 4.江苏省工程咨询中心，江苏 南京 210003；5.黄河水利科学研究院泥沙研究所，河南 郑州 450003)

确立水环境质量底线是提高区域水环境治理能力的重要途径，污染物总量控制是确立水环境质量底线的关键环节，而制定科学、合理、可行的水污染负荷优化分配方案则是实施污染物总量控制的关键技术[1-3]。

关于水污染负荷分配，国内外已有多位学者进行了深入研究，基于经济最优化原则和水环境容量总量控制目标，提出了均等分摊允许排污量、等比例削减现有排污量、区域内排污总量最小、区域内污染治理投资费用最小、公平分配允许排污量和削减量等方法[4-5]。其中，公平和效益是贯穿污染负荷分配的两个基本原则[6]。黄显峰等[7]以水质和效益最优为目标函数，构建针对单一河流排污权的多目标优化分配模型，即先将河流总体排放容量分配至水功能区，再逐级分配至排污单元。李如忠等[8]采用经济收益、污染削减费用作为经济性指标，加权综合基尼系数作为公平性指标，构建多目标优化模型进行水污染负荷分配。张璇等[9]提出了考虑环境保护税的双层多目标优化分配模型，实现了在环境保护税法与水功能区水质达标考核多重要求下，水污染负荷的优化公平分配。顾文权等[10]用模糊集理论量化了污染排放量和限制排放总量，并引入基于概率的全局寻优方法，避开了污水处理费用与限排目标间权重难以定量的问题，提高了污染负荷分配的效益性和公平性。基于公平和效益的多目标优化分配模型可以有效实现水污染负荷的优化分配，现有污染负荷优化分配中，针对点源污染负荷进行分配的研究成果较多，由于非点源污染负荷具有随机性、不确定性和难监测等特点，对其进行分配研究总体较少，自主研发模型少见，非点源污染负荷估算和分配是污染负荷分配研究的难点[11-16]。此外，现有的污染负荷优化分配多针对简单水系树状河网[17]或大尺度流域控制单元进行优化分配[18-20]，复杂水系，如平原河网地区，由于其河道纵横交错，水流流向顺逆不定，产汇流及产污关系不明晰，同一污染源可对流域内多个控制断面水质产生影响，水质时空变化具有高度的不确定性，因此，至今仍较少有文献对其进行点面源污染负荷优化分配的研究[4,11,12,21]。

本文基于考虑降雨产流及点面源产污时空分配的平原河网水动力、水质模型，以满足区域控制断面水质达标保证率、点面源环境管控要求及污染治理水平为约束条件，以点面源污染物最大允许排放量为目标函数，构建基于多控制断面水质达标保证率的点面源污染负荷优化分配模型；采用遗传算法求解，并选取太湖某河网区域对构建的模型进行了验证。

1 研究方法

1.1 响应关系识别

潮汐河网地区，水流流向、流量均可能随着区域水文情势的改变而发生变化。根据河网地区污染物迁移、转化特征，特定区域给定控制断面的污染物质量浓度与研究河网边界(入流边界)水量及污染物质量浓度、点面源污染物排放强度、底泥污染物释放强度等相关。对于特定的研究时段，控制断面污染物质量浓度时间变化过程是入流边界污染物通量、点源污染物排放、河网汇流区面源污染负荷、底泥污染物释放等在控制断面产生的质量浓度时间变化过程的线性叠加。

对于一个确定的有代表性、偏于水质安全的典型水文条件即设计水文条件，在确定的已知水流参数条件下，控制断面污染物质量浓度时间变化过程可表示为

ρ=f(ρB,wP,wN,wS)

(1)

式中：ρ为控制断面污染物质量浓度，mg/L；ρB为控制区域所有入流边界断面污染物质量浓度，mg/L；wP、wN、wS分别为控制区点源、面源、底泥相应的污染物释放强度，g/s。

1.1.1平原河网水动力模型

河网由若干单一河道组成，描述单一河道一维非恒定流的Saint-Venant方程组为

(2)

式中：t为时间，s；x为空间坐标，m；Q为流量，m3/s；Z为水位，m；B为水面宽度(包括主流宽度及仅起调蓄作用的附加宽度)，m；u为断面平均流速，m/s；A为过流断面面积，m2；n为糙率；R为水力半径，m；g为重力加速度，g=9.8 m/s2；q为旁侧入流流量，m3/s。采用三级联合解法[22]可得到单一河道各断面水位及流量时间变化过程。

1.1.2平原河网水质模型

描述河网中单一河道污染物质输移规律的基本方程为带源的一维对流扩散方程：

(3)

式中：Ex为纵向分散系数；K为污染物降解系数；S为单位时间、单位河长污染物排放量，kg/(s·m)。采用三级联合解法，可得到河网各节点、河道各断面污染物质量浓度时间变化过程。

1.1.3断面质量浓度与污染负荷响应关系时间序列

采用河网水动力、水质数学模型，通过控制变量法，可以计算得到设计水文条件(一般为典型枯水年)各入流边界断面污染物入流过程在控制断面j的污染物质量浓度响应时间变化序列(ρBj)，同理可计算点源排污、面源入流及底泥释放在控制断面j的污染物质量浓度响应时间变化序列(ρPj、ρNj、ρSj)：

(4)

式中：N为时间序列长度，N=365；ρBj,k、ρPj,k、ρNj,k、ρSj,k分别为时段k入流边界污染物、点源排污、面源入流、底泥释放在控制断面j的响应质量浓度。

污染物在地表水中迁移、转化过程满足扩散质对流扩散方程，属于一阶动力学系统，满足线性叠加原理。据此，控制断面j的污染物质量浓度时间变化过程可表示为

ρj=ρBj+ρPj+ρNj+ρSj

(5)

某一污染源在控制断面j的质量浓度响应时间变化序列可视为若干单位源强作用的线性叠加的结果，即有如下关系式：

ρij=Piαij

(6)

式中：ρij为污染源i在控制断面j贡献的污染物质量浓度时间变化序列；αij为污染源i的单位源强在控制断面j的质量浓度响应时间变化序列，将其定义为水质响应系数，表征控制断面j的水质对污染源i的响应关系；Pi为污染源i的源强。响应系数反映了在质量守恒原理基础上控制断面水质与污染源的定量关系，是污染负荷优化分配的基础。

1.2 优化分配模型

针对平原河网区水质的时空变化特征，引入水质达标保证率概念。以点面源允许排放量最大为目标函数，以满足区域控制断面水质达标保证率、点面源环境管控要求及污染治理水平为约束条件构建基于多控制断面水质达标的点面源污染负荷非线性优化分配模型。模型目标函数和约束条件为

(7)

(8)

式中：W为所有点面源排污入河量的总和；P(·)为多控制断面水质达标事件成立的概率；WSm为城镇及农村生活面源m的排污入河量；WNr为农业生产面源r的排污入河量;WWk为污水处理厂点源k的排污入河量；WPl为工业直排点源l的排污入河量；WSm,0、WNr,0、WWk,0、WPl,0分别为各点面源现状排污入河量；ASm,max、ANr,max、AWk,max、APl,max分别为各点面源污染物削减率的上限；ASm,min、ANr,min、AWk,min、APl,min分别为各点面源污染物削减率的下限；αmj、αrj、αkj、αlj分别为各点面源在控制断面j的响应系数；ρuj为控制断面j的上游来水响应质量浓度；ρcj为控制断面j的水质控制标准质量浓度；βfj为控制断面j的水质达标保证率要求(一般取值为90%)。

采用遗传算法求解线性目标函数的非线性约束问题，求解步骤为[23]：①设置运行参数；②生成初始种群；③评价个体适应度与选择运算；④交叉运算；⑤变异运算；⑥产生新一代种群。由此得到的全局优化最优解即为研究区域内各污染源允许排放量组合，此排放量组合满足多个控制断面的水质管控目标。

2 算例验证

2.1 研究区概况

研究区位于江苏省宜兴市，地处太湖以西，滆湖以南，属太湖流域南溪水系，为典型平原河网。主干河流(南溪河、北溪河、邮芳河)汇集流域支流水量后经西氿、团氿和东氿3个小型湖泊，于大浦港、城东港、洪巷港汇入太湖。其中西氿大桥断面与洪巷桥断面为该水系水环境质量控制代表断面，水质目标均为地表水Ⅲ类。研究区域年平均降雨日 136.6 d，年平均降水量1 177 mm，春夏雨水集中，西氿水位与上游南溪河来水呈正相关，研究区域水系及水质控制代表断面如图1所示。

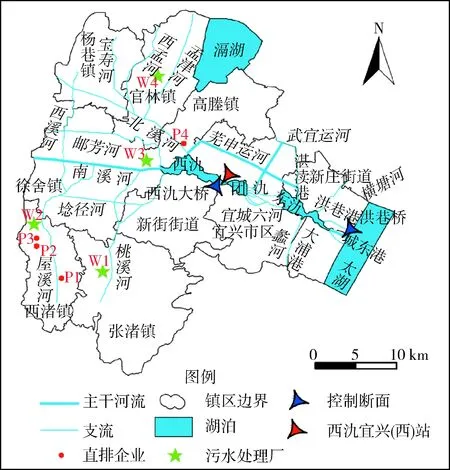
图1 研究区域水系及水质控制代表断面

2.2 河网水动力模型模拟与验证

a.边界条件。根据流域长系列年降水量资料进行频率分析，选取与90%水质达标保证率相匹配的2000年为设计枯水典型年[24]，通过太湖流域水动力边界提取水位或流量时间变化过程作为边界条件，共13个流量边界，4个水位边界，河网区域概化如图2所示。对于降雨产流入河过程，按空间位置关系识别陆域单元与入流河段的对应关系[22]，再根据产流系数计算各单元产流量，最后按时间分配比例确定陆域产流入河的时间分配过程，实现陆域产流与河网汇流的时空耦合。

图2 研究区域河网概化示意图

b.参数取值及模型验证。参照该地区历史研究成果确定河道糙率取值范围0.017～0.025[21,25]，采用西氿宜兴(西)站(如图1)2000年逐日水位观测资料进行验证，水位计算值与实测值对比结果如图3所示，对比显示水位计算值与实测值吻合，平均误差0.03 m。

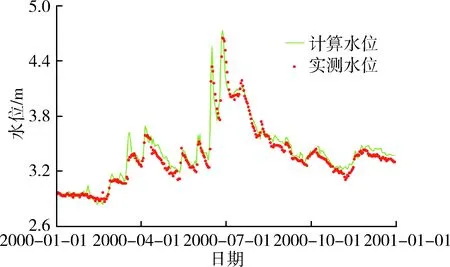
图3 2000年西氿宜兴(西)站逐日水位计算值与实测值对比

2.3 河网水质模型模拟与验证

a.边界条件。根据入流边界相邻上游水体水功能区划对应的水质目标，确定入流断面污染物质量浓度时间变化过程，对于出流边界，设定边界上污染物质量浓度梯度为常数，即采用第二类边界条件。

b.点面源概化。研究区域共有8个点源排污口，首先确定排污口位置与计算子河段的对应关系。根据陆域产汇流单元与河道对应关系，识别陆域单元产污与入流河段的对应关系[22]，再根据降雨产流、面源污染物质量浓度时间变化过程获得试验经验值，确定陆域产污入河的时间分配过程，实现陆域面源产污负荷与河网污染物输运的时空动态耦合。

c.参数取值及模型验证。根据该区域相关研究成果确定污染物降解系数，其中氨氮(NH3-N)降解系数取值范围为0.06～0.09 d-1，总磷(TP)降解系数取值范围为0.06～0.1 d-1。采用西氿大桥、洪巷桥断面2015年水质监测数据进行验证，水质计算值与实测值对比结果如图4所示。西氿大桥断面氨氮、总磷质量浓度计算结果的平均相对误差分别为14.95%和17.13%，纳什效率系数分别为0.91、0.36；洪巷桥断面氨氮、总磷质量浓度计算结果的平均相对误差分别为11.71%和14.23%，纳什效率系数分别为0.83、0.91。模型模拟效果较好，可用于研究区域河网水系内污染物输移、转化的动态变化过程。

2.4 分配结果与讨论

通过对研究区域现有污染物处理技术及各行政单元对污染负荷管控要求的研究，确定污染物削减率上、下限取值分别为ANr,min20%、ANr,max100%、APl,min60%、APl,max80%、ASm,min60%、ASm,max80%、AWk,min10%、AWk,max40%，研究区域氨氮、总磷污染负荷分配结果见表1。由表1可见，农业生产面源、工业直排点源、生活面源、污水处理厂点源氨氮削减率范围分别为30%～53%、50%～64%、73%～76%和29%～30%；总磷削减范围分别为33%～49%、57%～60%、71%～76%、29%～30%。农业生产面源削减率范围主要受污染源所处地理位置影响，控制生活面源、工业直排及污水处理厂点源污染物削减率是现行污染减排关键。

(a) 氨氮(西氿大桥断面)

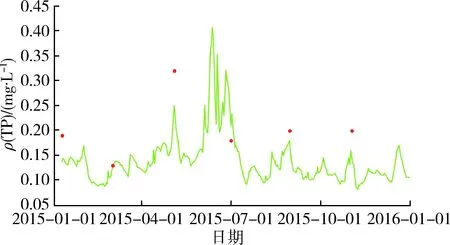
(b) 总磷(西氿大桥断面)

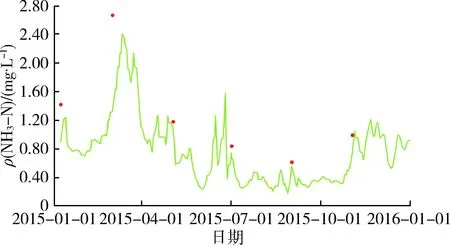
(c) 氨氮(洪巷桥断面)

(d) 总磷(洪巷桥断面)

表1 研究区域氨氮、总磷污染负荷分配结果

根据污染负荷分配结果，设定点面源排放量，在设计水文条件下，采用河网区水动力、水质模型，计算得到各水质因子各断面典型水文年的质量浓度变化过程，如图5所示，图中ρS(NH3-N)和ρS(TP)分别为氨氮和总磷达到地表水Ⅲ类水标准的质量浓度。达标时间统计分析结果显示，西氿大桥断面氨氮、总磷达标时间频率分别为90.68%和90.96%，洪巷桥断面分别为92.05%和95.89%，各控制断面氨氮、总磷质量浓度的全年水质达标保证率超过90%。研究区域点面源污染负荷优化分配结果合理可行，所建模型有效。

(a) 氨氮

(b) 总磷

3 结 语

本文基于公平和可行性原则，提出了一种基于多控制断面水质达标的平原河网区点面源污染负荷优化分配模型。针对平原河网复杂水系特点，构建考虑降雨产流及面源产污时空分配的平原河网区水动力及污染物迁移数学模型，明确典型水文年设计水文条件下，点面源在各控制断面的水质响应关系。引入水质达标保证率概念，将随机分析方法与确定性水质数学模型相结合，以点面源污染物最大允许排放量为目标函数，以满足多控制断面水质达标保证率、点面源环境管控要求及污染治理水平为约束条件，将基于多控制断面水质达标的点面源污染负荷优化分配问题转化为线性目标函数非线性约束条件的极大值问题。

太湖某典型区域算例的验证表明，该模型系统、直观地反映了点面源污染负荷优化分配结果，克服了优化分配模型应用于复杂水系可行性的不足，为基于水质改善的污染物总量控制管理提供有效可靠的技术支撑。