基于因子分析的供水管网健康状态评价指标遴选
丁相毅,石小林,凌敏华,黄 泽,安 琪,刘思然
(1.中国水利水电科学研究院水资源研究所,北京 100038; 2.郑州大学水利科学与工程学院,河南 郑州 450001;3.吉林大学新能源与环境学院,吉林 长春 130012)
供水管网健康状态评价结果是城市供水管网维护更新的重要理论依据,而评价指标的确定和指标数据的收集是评价过程中的关键,对于提高评价结果的科学性和准确性起到了重要作用。城市供水管网系统是一个构件繁多、结构复杂、工况时刻都在变化且充满不确定性的庞大系统,用一两个指标难以科学全面地评价其健康状态,但如果指标选择过于复杂,又会使得数据处理变得混乱与困难[1]。在供水管网健康评价指标的研究当中,国际水协会(IWA)和美国自来水厂协会(AWWA)推荐用供水设施漏失指数(infrastructure leakage index, ILI)作为最合适和最实用的性能指标来表征真实漏失量(物理漏失量)[2];Pelletier等[3]研究了供水管道10年来的破损记录,将每年水管破裂的数量作为管网结构状态的指标;张现国等[4]通过比较国际水协、世界银行、澳大利亚、葡萄牙以及我国现行的漏损水量评价指标,分析供水管网漏损影响因素,探讨了漏损评价指标的筛选;余鹏钧[5]通过对南方某市的管道健康影响因素的分析,开展了南方某市供水管网健康评价指标体系的构建研究;代焕芳[6]建立了用于评价供水管网漏失水平的指标——背景漏失指数(background losses index, BLI)并对其实用性进行了验证;王旭冕等[7]利用统计学知识,建立了由方差分析、综合评价指标分析和极大不相关分析组成的三步筛选法筛选参与聚类分析的指标,剔除了对聚类分析产生干扰的重复、多余或片面指标。总体来说,目前对供水管网健康状态评价指标的代表性和敏感性研究较少,因此本文对供水管网健康状态评价指标进行贡献度分析及敏感度分析,遴选出代表性强、敏感度较高的指标,以期为供水管网健康状态评价指标体系的建立和指标数据收集等基础工作提供借鉴和参考。
1 数据与方法
1.1 数据来源
1.1.1供水管网健康状态评价指标选取
根据供水管网健康概念和内涵,综合考虑管网健康状态的影响因素[8],对比分析国内外大量的相关文献[3-8],并结合我国供水管网运行实际情况,根据选取指标的代表性、完备性、相对独立性和可操作性的原则,初步筛选了20个指标构成初选评价指标体系,其中管网静态结构指标12个、水力指标5个、水质指标3个。然后根据供水管网维修情况概率统计并结合专家主观判断,最终确定11个供水管网健康状态评价指标,其中供水管网静态结构影响因素7个,供水管网水力和水质影响因素分别有2个,具体见图1。

图1 供水管网健康状态评价指标体系
1.1.2供水管网静态结构指标数据来源
本文以浙江省云和县供水管网为研究实例,数据源于云和县水利局和云和县供排水公司提供的2017年云和县供水管网基本属性情况统计资料、2010—2017年云和县供水管网维修情况统计资料、2017年云和县部分供水管道水力、水质监测数据资料、2017年云和县供水管网CAD图等。其中,部分供水管网静态结构影响指标数据需依据相关资料运用专家打分的方法获得[9-10],共邀请8位专家对管材、接口形式、地面荷载、内外衬层这4个指标按供水管网健康程度进行评分,设定其评分最高值为1,即供水管网健康状态最优;最低评分为0,即供水管网健康状态最差。专家评分汇总情况见表1。
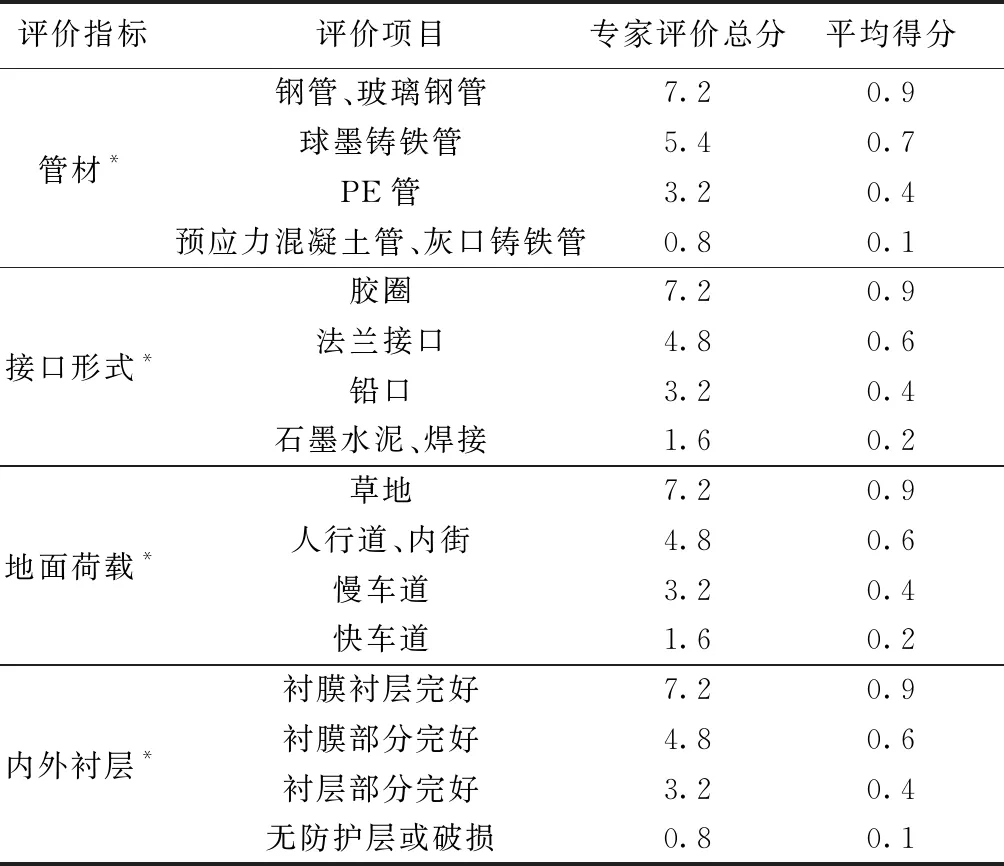
表1 专家评分汇总
1.1.3供水管网水力、水质指标数据来源
真实的供水管网是一个非常复杂且庞大的系统,管网水力、水质数据的采集具有极大的困难性。本文根据云和县供水管网基本属性情况统计资料、2017年云和县部分供水管道水力、水质监测数据资料和云和县供水管网CAD图等基础资料,按照一定的概化原则,对云和县供水管网进行管段概化、节点合并等处理,省略了对水力、水质条件影响较小的管线,保留DN100以上的主要干管,最后运用EPANET软件建立供水管网微观模型,建立供水管网拓扑结构(图2),模拟得到供水管网水力、水质数据。云和县供水管网水力、水质数据指标样本数为108,概况见表2。
1.2 基于因子分析确定贡献度的方法
因子分析可将具有错综复杂关系的变量综合为数量较少的几个因子,用以展现原始变量与因子之间的相互关系[11]。然后将相关性较强的几个变量归在同一个类中,每一类赋予新的名称成为一个因子,用于反映事物的一个方面或者一个维度[12]。本文使用因子分析原理中因子对原资料信息的解释性的含义,即,因子方差越大,该因子对整个样本的贡献度越大、解释力度越强,通过计算因子得分和因子方差贡献率确定各评价指标对供水管网健康状态的贡献度大小。该方法的步骤为
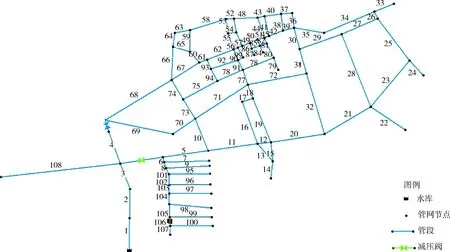
图2 云和县供水管网拓扑结构
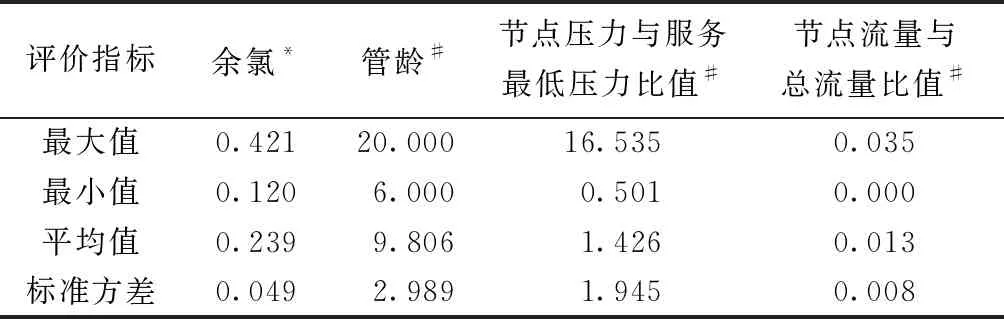
表2 云和县供水管网水力、水质指标概况
步骤1将逆向指标数据添加负号进行正向化处理[13],在此基础之上建立原始数据矩阵。设有n根管道作为样本,每根管道有p个指标,这样就构成了一个n×p阶的矩阵Xn×p。
步骤2数据标准化。由于不同的评价指标常常具有不同的单位,为了消除量纲和数量级的影响,需要对原始指标进行标准化处理[14],得到标准化后的各指标数据矩阵X′,计算公式为
(1)
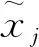
步骤3计算(X′ij)n×p的相关系数矩阵R。
步骤4用雅克比方法求相关系数矩阵R的特征值(λ1,λ2,…,λp)和相应的特征向量αi=(αi1,αi2,…,αip),其中i=1,2,…,p。
步骤5计算因子方差贡献率。因子方差贡献率的计算公式为
(2)
因子累计方差贡献率的计算公式为
(3)
式中m为p个指标经过降维后的因子个数。
步骤6计算旋转后的因子荷载矩阵。当初始因子在原变量上的载荷值都相差不大,各因子的典型代表变量不突出时,容易使因子的意义含糊不清,不便于对因子进行解释[15]。为了便于对实际问题进行分析,需要进行旋转使因子载荷矩阵中载荷的绝对值向0和1两个方向分化,从而更清楚地解释因子的含义。因子旋转一般采用方差最大化正交旋转[16-17]。
步骤7计算因子得分。计算公式为
Fj=βj1X′1+βj2X′2+βj1X′2+…+βjpX′p
(j=1,2,…,m)
(4)
式中:Fj为各因子得分;β为各因子得分系数矩阵。
步骤8计算各指标贡献度和综合得分。由因子得分系数的含义可知,因子得分系数是样本中各个指标对因子的贡献,而方差贡献率是因子对所有样本方差的代表。因此,因子得分系数与相应方差贡献率的乘积即为各指标在样本中的贡献[18],然后再对其进行归一化处理。计算公式为
(5)
式中wi为第i个指标的贡献度。
根据因子得分和因子方差贡献率计算综合得分:
|Z|=|F|×|e|
(6)
式中:|Z|为样本综合得分矩阵;|F|为因子得分矩阵;|e|为因子方差贡献率矩阵。
1.3 敏感性分析方法
敏感性分析亦称敏感度分析[19],研究如何将模型结果的不确定性分配到不同的模型输入参数中,从而筛选出引起模型结果不确定性的主要影响因素,识别和选择关键控制参数,该方法一般用于投资项目评价时分析不确定性因素对项目经济效益指标的影响程度和敏感性程度。分析影响程度的大小称为该属性的敏感性系数[20],敏感性系数绝对值越大,说明该属性对模型输出的影响越大[21]。目前,分析敏感性的方法有局部分析法、全局分析法、定性方法和定量方法[22]。本文利用非参数统计方法计算敏感性系数(敏感度),公式为
(7)
式中:SRCi为第i个指标评价敏感度;σi和σy分别为第i个指标因子和样本综合得分的标准方差;bi则为y关于x的回归系数。

表3 SPSS软件计算结果
2 结果与分析
2.1 因子分析结果
在进行因子分析前,首先要检验指标变量因子是否适合做因子分析[23]。本文利用SPSS26.0软件对11个供水管网健康评价指标进行KMO检验和Bartlett球形检验,检验结果表明,抽样适度的KMO测定值为0.659,Bartlett球形检验显著性为0.000。根据Kaiser常用度量标准,当KMO值高于0.6时,整个样本就可以做因子分析,同时Bartlett检验的Sig即p值接近于0,远小于显著水平0.05,因此拒绝Bartlett球形检验的0假设,该样本数据适合做因子分析[24]。
利用SPSS软件计算样本数据旋转后的特征值与因子累计方差贡献率,结果见表3,可见,提取的4个因子旋转后的特征值均大于1,累计方差贡献率达到了76.226%,说明提取出来的4个因子可以反映11个指标当中76.226%的信息量,虽然没有大于80%的传统经验值,但超过了75%,总体上因子分析的结果还是可以接受的。
为使各指标更好地解释因子,使得各因子的典型代表指标更加突出显示,利用SPSS软件中方差最大化法对因子荷载矩阵进行旋转并按照从大到小的顺序进行排序,结果见表4。查找相关系数显著性检验表,可以看出在0.01显著性水平上,相关系数绝对值大于0.25,就可以认为此相关系数在0.01水平上显著。为科学起见,本文以荷载度0.5以上为提取依据,对4个因子当中原始指标进行归纳分析,发现因子1包括覆土厚度、接口形式和管径3个指标,其中覆土厚度对因子1的相关度最大且达到了0.932,相对而言,其他两个指标对因子1的相关度就比较小,由荷载矩阵含义可知,该指标与因子1越密切,对因子1的代表性越高,所以因子1可以命名为外部环境对管道静态结构的影响;因子2包括管龄、内外衬层、地面荷载和管材,整体而言,管龄、内外衬层和管材都是反映管道内部静态结构的情况,所以因子2可以命名为管道内部静态结构影响因素;因子3包括节点水龄、余氯、节点压力与服务最低压力比值,整体而言,节点水龄和余氯反映的是管道内水质的情况,所以因子3可以命名为水质影响因素;因子4包括节点流量与总流量比值,该指标反映的是管道内水压的情况,所以因子4可以命名为水力影响因素。
2.2 贡献度计算结果
根据式(4)和式(5),计算各个指标对于整个样本的贡献度并进行排序,具体结果见表5。由贡献度的含义可知,贡献度越大,该指标对于整个样本评价时就越重要,当累积贡献度越大,则说明选取的系列评价指标对于提高样本综合评价结果的全面性和合理性就越好。由表5可见,内外衬层和管径贡献度排名靠前,说明这两个指标对供水管网健康状态的评价非常重要;还发现内外衬层、管径、节点流量与总流量比值、余氯、节点压力与服务最低压力比值、覆土厚度、管材、管龄累计贡献度达到0.80,反映出这8个指标能比较全面和合理地解释供水管网的健康状态,所以在管网健康状态评价时这8个指标属于必选的评价指标,然后再根据实际情况在这8个指标的基础之上增加其他合适的指标,使累积贡献度尽可能接近1。从因子命名角度分析,上述8个指标在4个因子当中均有体现,而且在建立的供水管网健康状态评价指标体系的三大影响因素里均有所表征,说明这8个指标能够对供水管网健康状况做一个基础且相对全面的解释,因此将上述8个指标作为基础必选的评价指标是科学合理的。同时,也反映出单从供水管网静态结构影响因素、管网水力影响因素或管网水质影响因素出发建立供水管网健康状态评价指标体系,并不能很好地诠释供水管网的实际健康状况,而应该同时考虑供水管网静态结构影响因素、管网水力影响因素和管网水质影响因素,建立“三位一体”(管内-管道-管外)的供水管网健康状态评价指标体系。
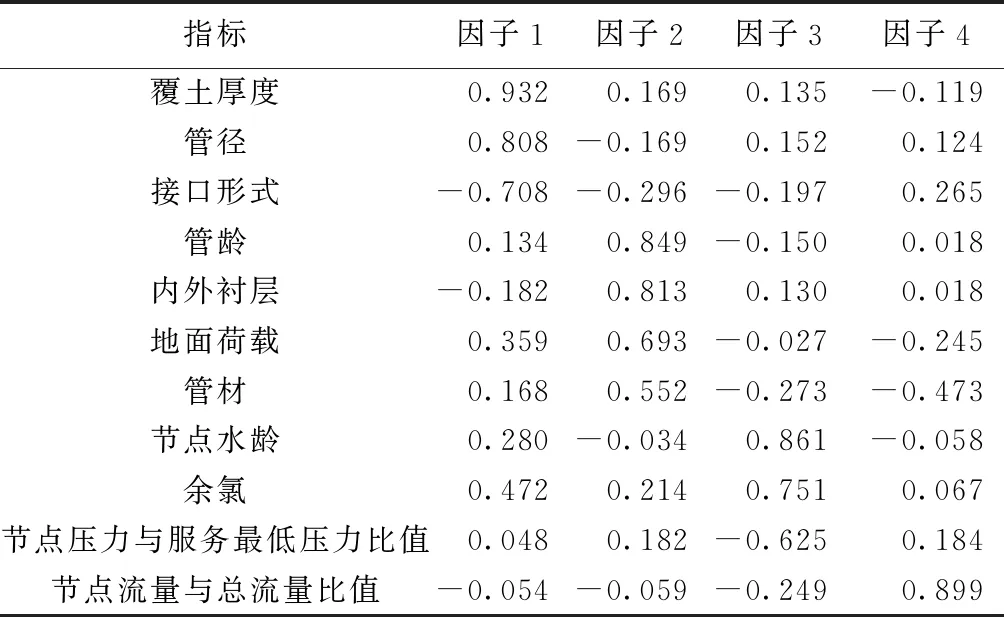
表4 旋转后的因子荷载矩阵
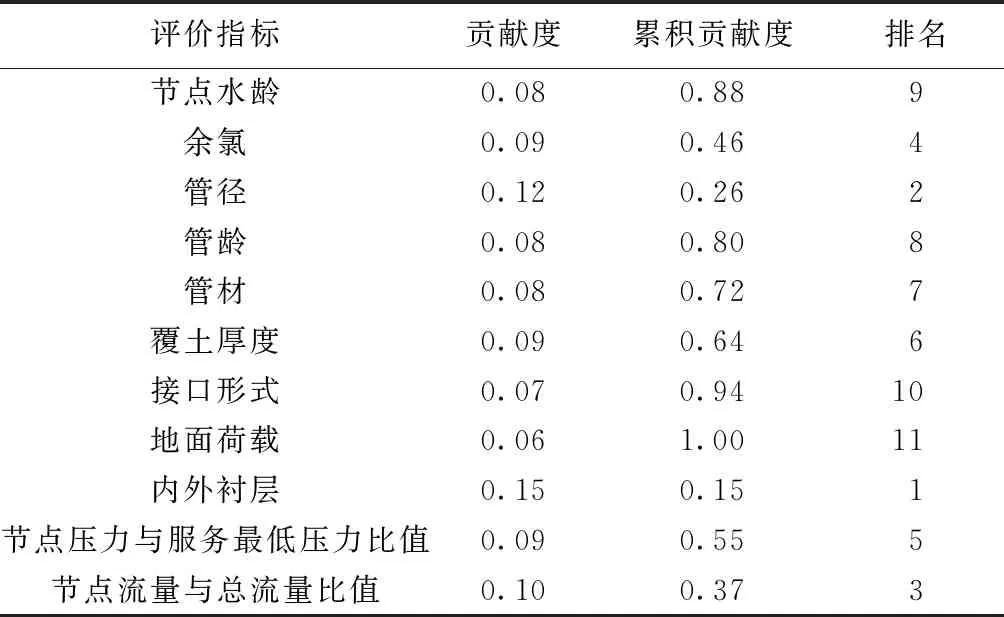
表5 贡献度计算结果
2.3 敏感度计算结果
根据式(4)和式(6)计算管道综合得分,利用SPSS26.0软件确定综合得分关于各个指标的回归系数,最后根据式(7)计算各个指标的敏感度并按照从大到小的顺序进行排序,计算结果见表6。由表6可见,余氯和节点流量与总流量比值敏感度排名靠前,说明在这11个指标当中,余氯和节点流量与总流量比值对供水管网健康影响程度较大。为提高评价结果的准确性,应该提高这两个指标的数据精确度。分析两个指标数据来源可以发现,余氯属于水质影响因素,节点流量与总流量比值属于水力影响因素,而管网水力、水质指标数据均源于EPANET软件建模模拟所得,因此,尽量减小模型误差将是提高管网健康评价结果准确性的关键。
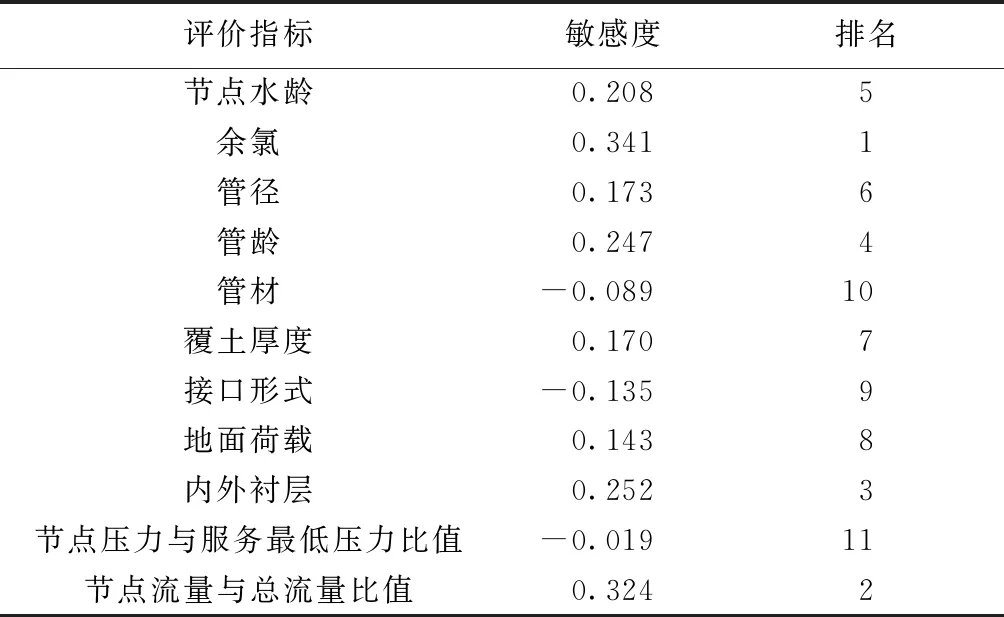
表6 敏感度计算结果
2.4 敏感度和贡献度结果对比
由于贡献度和敏感度属于不同的领域范畴,不宜直接从计算结果的大小做对比分析。本文着眼于排名结果的变化情况,通过分析各个指标贡献度和敏感度排名的变化来研究各个指标对供水管网健康状态的代表性和敏感性。根据各个指标贡献度和敏感度排名结果(表5、表6),可见,有6个指标贡献度排名和敏感度排名均在前8位,分别是内外衬层、管径、节点流量与总流量比值、余氯、覆土厚度、管龄,除节点压力与服务最低压力比值排名差异大以外,其余评价指标排名差值均在4及以内,排名差异属于可接受范围,因此可以认为指标贡献度越大,其对应的敏感度一般也偏大。节点压力与服务最低压力比值贡献度排名虽较靠前,但是它的敏感度排名却处于最末,说明该指标在允许的范围内变化对供水管网健康状态评价结果影响程度较小,但是如果该指标过小,满足不了用户对于用水水压的需求,如果指标过大,则容易发生爆管,因此,该指标对于供水管网健康状态的表征又显得非常重要。
3 结 论
本文运用统计学的方法,把11个供水管网健康状态评价指标划分为4层,即外部环境对管道静态结构影响因素、管道内部静态结构影响因素、水质影响因素、水力影响因素;分析了各个指标对于整个样本的贡献度大小,提取出了8个最为重要和基础的指标,分别是内外衬层、管径、节点流量与总流量比值、余氯、节点压力与服务最低压力比值、覆土厚度、管材、管龄;在此基础上分析了各个指标敏感度,筛选出了贡献度和敏感度排名均在前8位的6个指标,分别是内外衬层、管径、节点流量与总流量比值、余氯、覆土厚度、管龄。为提高评价结果的科学性和准确性,贡献度前8位的指标应该作为基础的必选指标,并且应尽量提升内外衬层、管径、节点流量与总流量比值、余氯、覆土厚度、管龄数据的精度。

