基于TL矩法的洪水频率分布参数估计方法优选
贾一凡,宋松柏
(1.西北农林科技大学水利与建筑工程学院,陕西 杨凌 712100; 2.西北农林科技大学旱区农业水土工程教育部重点实验室,陕西 杨凌 712100)
洪水是最常见的自然灾害之一,利用有限的水文观测资料发掘洪水规律,并据此制定相应的预防措施可以避免或减少不必要的损失[1]。洪水频率分析通过选定的频率分布来估计洪水特征值,预测未来事件的发生概率。洪水频率分布参数的合理估计,直接影响洪水设计值计算的合理性。由于气候变化及人类活动的影响,洪水的驱动机制及发生规律等出现了显著的变化,针对这些变化,近年来国内外学者不断开展洪水频率分析的不确定性研究,以提高洪水预报精度[2-5]。
洪水频率分析的关键步骤为频率分布线型及参数估计方法的选择,它们决定了拟合的效果[6]。目前较为广泛使用的频率分布有P-Ⅲ分布、对数P-Ⅲ分布、广义Pareto分布(GPA)、广义极值分布(GEV)、广义Logistic分布(GLO)和Gamma分布等。常用的参数估计方法有矩法(MOM)、线性矩法(LM)、极大似然法(MLE)、适线法及概率权重矩法(PWMM)等[7],这些方法各有优缺点,在不同实例中应用时会产生较大差异[8]。极大似然法估计的参数是渐近有效和无偏的,因此优于矩法[9],但它求解过程烦琐。传统矩法采用样本矩代替总体矩,原理简单,实际应用方便,但是偏态系数会产生较大误差,导致该方法不能轻易作为单独的估计方法来使用[10],通常与其他方法参照应用[11]。相比传统矩法,线性矩法受样本变异性的影响较小,具有良好的不偏性。同时,对于数据中的异常值,线性矩法比传统矩法更加稳健,并且能从小样本中推断可能的概率分布[12],但该方法的缺点是对水文极值序列中极大值和极小值反应不敏感。
在线性矩法的基础上,进行大幅度修改的TL矩法(TLM)[13]于2003年被提出,该方法对极端观测值分配零权重,消除了小样本序列中零值产生的不利影响。从总体线性矩的意义上来说,在TL矩中,概念样本次序统计量的期望被较大样本次序统计量的期望所代替,其增加的样本数量等于修正的总量,所以TL矩相比线性矩和传统矩具有一定的优势[14]。从TL矩法提出至今,国外学者解决了该方法的实际应用问题。Ahmad等[15]对GPA、GEV、GLO分布的TL矩法(修正量t1=1,t2=0)参数估计式进行了推导。Mat等[16]整理计算出了三参数对数正态分布和P-Ⅲ分布的TL矩,其中修正量t1=1,2,3,4。TL矩法在实际应用中存在修正量的选择问题,Ahmad等[17]研究表明,与TL矩法和线性矩法相比,仅调整最小值的TL矩法(修正量t1=1,t2=0)在估计高流量分位数方面具有更高的精度,它能够减少小样本值的不利影响。由于TL矩法的优越性,TL矩法逐渐应用于洪水频率分布参数估计[18-25]。
线性矩法是使用较为成熟的一种参数估计方法,在洪水频率分析中应用广泛,而基于线性矩法发展起来的TL矩法在一些研究中表现出较好的拟合效果。目前,我国还缺乏该方法的普适性研究。本文以陕北地区神木、绥德、杏河、刘家河、黄陵和志丹6个水文站的年最大洪峰流量序列为例,选取常用的3个三参数分布(GPA、GEV、GLO),分别用极大似然法、线性矩法及TL矩法进行参数估计,采用确定性系数(R2)和均方根误差(RMSE)进行分布线型及参数估计方法优选[26]。
1 3种概率分布参数的TL矩法估计
Hosking[12]将线性矩定义为概率权重矩的线性组合。假设随机变量X是样本容量为r的样本,X1:r≤X2:r≤…≤Xr:r表示相应的次序统计量,其定义的线性矩为
(1)
式中E(Xr-k:r)为容量为r的样本中第r-k位的次序统计量的期望值。
L-偏态系数和L-峰度系数为
(2)
从样本次序统计量X1:n≤X2:n≤…≤Xn:n中估算样本线性矩[18]:
(3)
式中n为样本容量。
Elamir等[13]提出的TL矩法在线性矩法的基础上进行了大幅度的修改,将样本容量r替换为r+t1+t2,其中增加的样本数量为t1个概念样本中的最小值与t2个概念样本中的最大值个数之和。因此,式(1)中的E(Xr-k:r)替换为E(Xr+t1-k:r+t1+t2)。在TL矩法的研究中,主要问题是修正量t1和t2的选择,经过经验及理论验证,样本中较小的值会影响高分位数估计时的准确性,因此仅修正最小值即t2=0时就可以得到准确的结果。研究[15,27-28]表明,修正量t1=1、t2=0时TL矩法能得到更好的参数估计结果,因此本文取t1=1,t2=0。
将r阶的TL矩定义为
(4)
取t1=1,t2=0,得到前4阶TL矩:
(5)
(6)
(7)
(8)
(9)
从样本次序统计量X1:n≤X2:n≤…≤Xn:n中估算样本TL矩:
(10)
样本TL-偏态系数与样本TL-峰度系数计算公式为
(11)
a.GPA分布参数的TL矩法估计。GPA分布的分位数函数为
(12)
对应TL矩法参数估计式[29]为
(13)
(14)
(15)
b.GEV分布参数的TL矩法估计。GEV分布的分位数函数为
(16)
对应TL矩法参数估计式[15]为
(17)
(18)
(19)
c.GLO分布参数的TL矩法估计。GLO分布的分位数函数为
(20)
对应TL矩法参数估计式[17]为
(21)
(22)
(23)
2 数据资料
选取陕北地区神木、绥德、杏河、刘家河、黄陵和志丹6个水文站的年最大洪峰流量资料,开展基于极大似然法、线性矩法和TL矩法的参数估计方法对比研究,进行GPA、GEV、GLO 3种三参数分布的曲线拟合,选用确定性系数和RMSE准则分析不同频率分布及不同参数估计方法下的拟合效果。经审查,选用资料满足一致性、可靠性及代表性要求,可用于计算。具体资料系列长度如表1所示。

表1 洪水资料系列长度
2.1 参数估计及曲线拟合
利用Matlab编程,将GPA、GEV、GLO 3种三参数分布通过极大似然法、线性矩法及TL矩法计算得到α、ξ和k3个参数值,参数估计结果如表2所示。
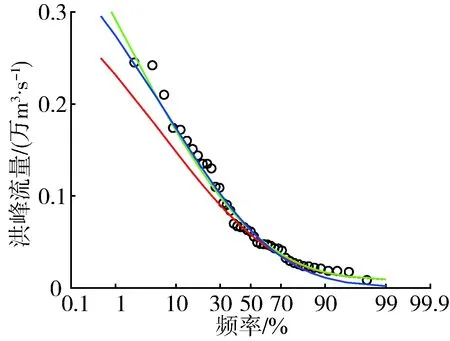
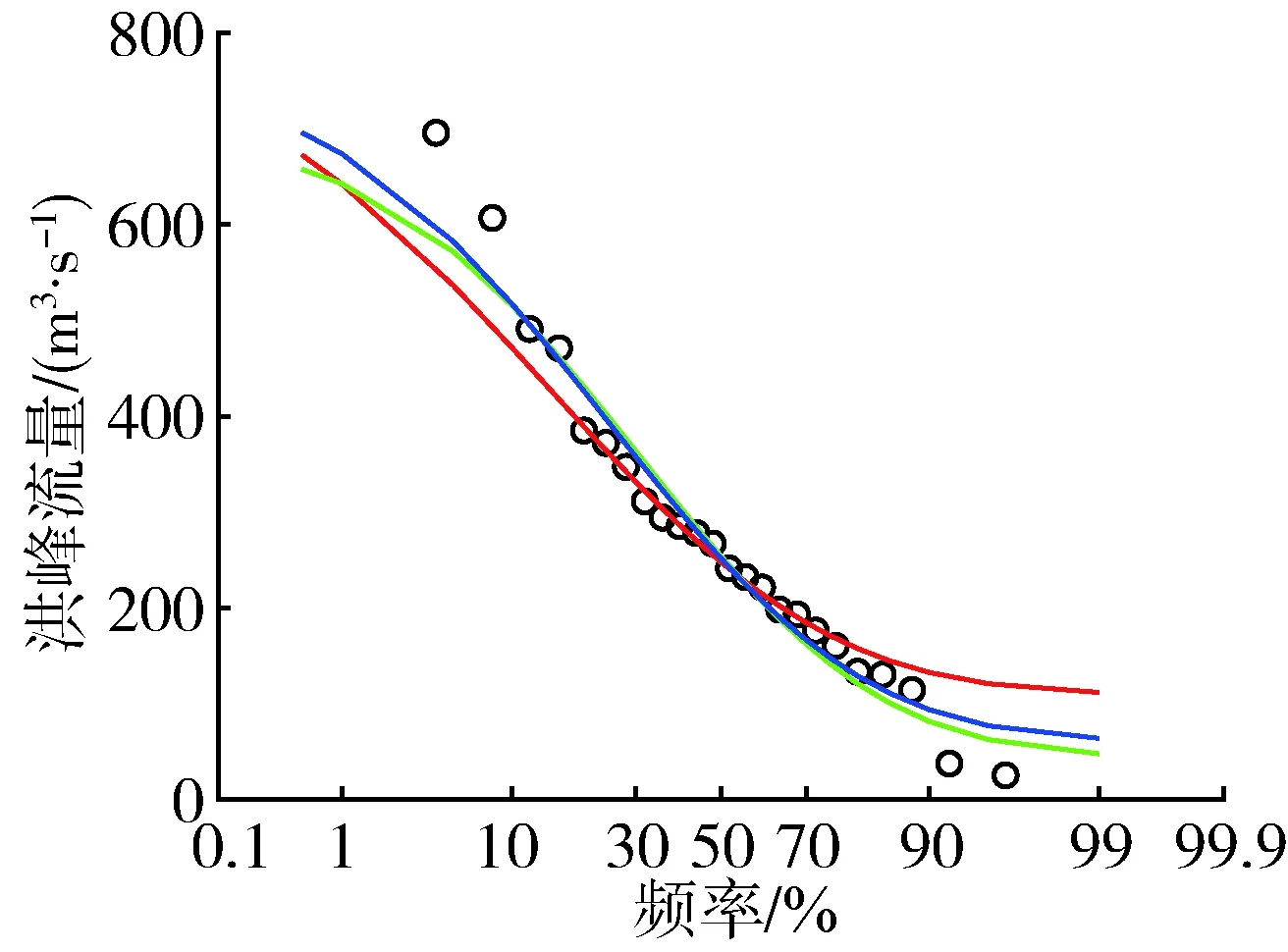
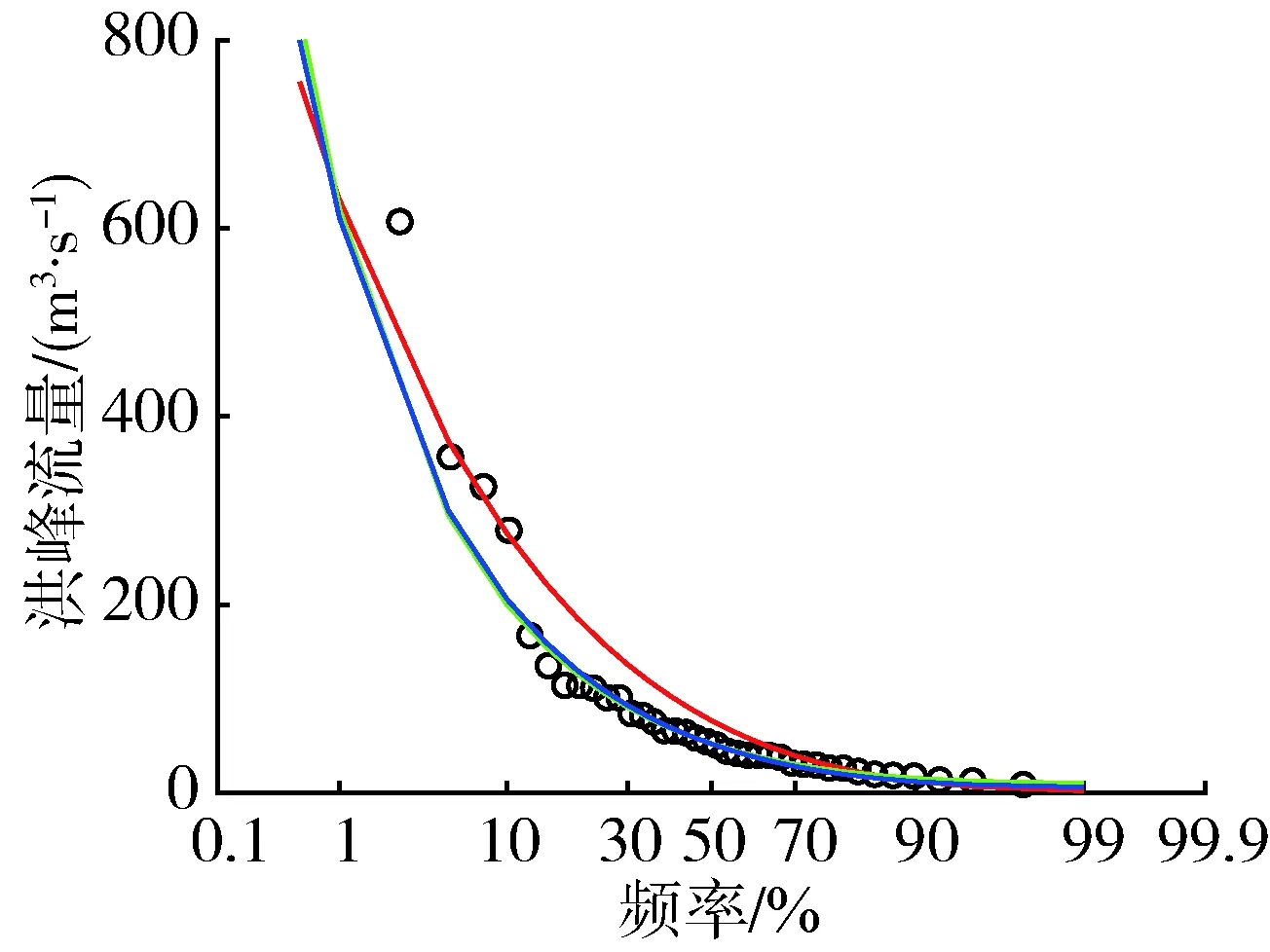
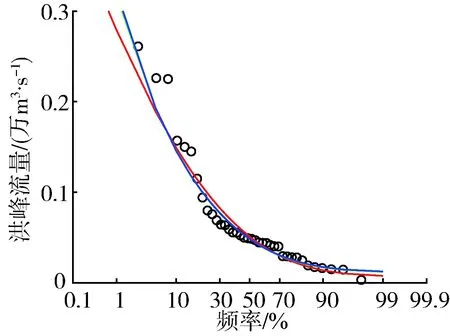
分析3种参数估计方法下的3种分布线型对经验点据的拟合情况,绘制频率曲线,以GPA分布线型为例,结果如图1所示。
从图1可以看出,整体上线性矩法与TL矩法的拟合效果优于极大似然法,能兼顾到经验点据各部分。神木站和绥德站上尾部分TL矩法拟合效果更好,下尾部分拟合效果不及极大似然法与线性矩法;刘家河、黄陵和志丹站线性矩法与TL矩法拟合效果相当且优于极大似然法。结合实际来看,洪水频率分析中更为注重上尾部分的拟合,因此TL矩法在上尾部分较优的拟合效果更有利于洪水设计值的选定。
2.2 拟合优度评价
确定性系数通常用于判断观测值与设计值的拟合程度,它是频率分布优选的常用指标之一。确定性系数值越接近于1,表明设计值越接近于实际观测值,即拟合效果越好。各站年最大洪峰流量序列不同参数估计方法确定性系数计算结果如表3所示。
从表3结果来看,除杏河站之外的其他5个水文站GPA分布确定性系数值均大于GEV分布以及GLO分布,依据数值接近1的原则,得出神木、绥德、刘家河、黄陵和志丹5个水文站选用GPA分布来描述更合适,GEV分布次之。而杏河站GEV分布的确定性系数值相比GPA分布与GLO分布要更接近于1,选用GEV分布拟合效果最优,GLO分布次之。由于杏河站年最大洪峰流量序列长度远小于其他5个水文站,小样本量可能会影响频率分布线型的选择而产生误导性结果,因此认为该区域用GPA分布拟合年最大洪峰流量序列较为准确。

表2 各水文站年最大洪峰流量序列分布参数估计结果


(a) 神木
(b) 绥德
(c) 杏河

(d) 刘家河
(e) 黄陵
(f) 志丹
2.3 误差分析
选取RMSE来定量评价参数估计方法,并进行参数估计方法优选。RMSE能衡量观测值与设计值之间的偏差,RMSE值越小拟合效果越好。各水文站对应RMSE值如表4所示。
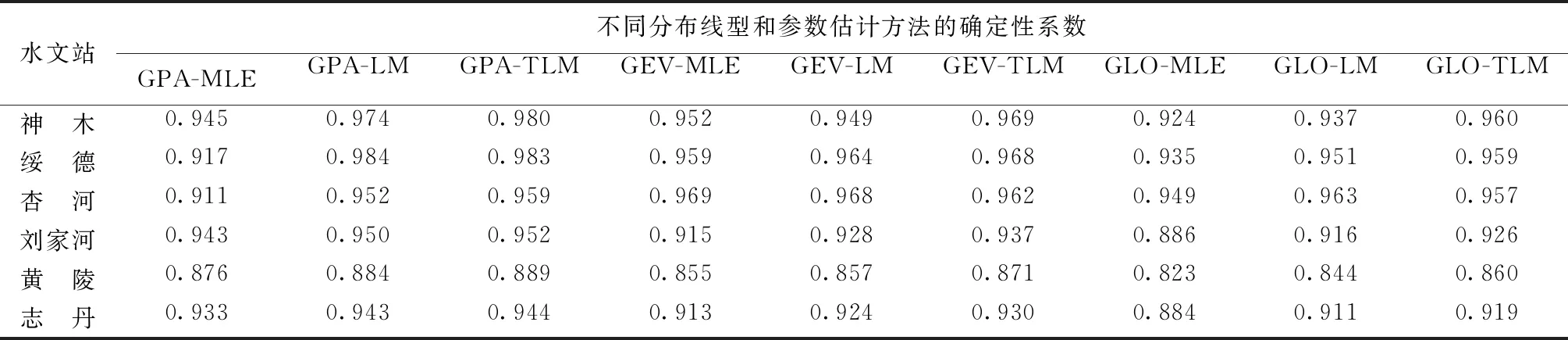
表3 各水文站年最大洪峰流量序列不同参数估计方法确定性系数
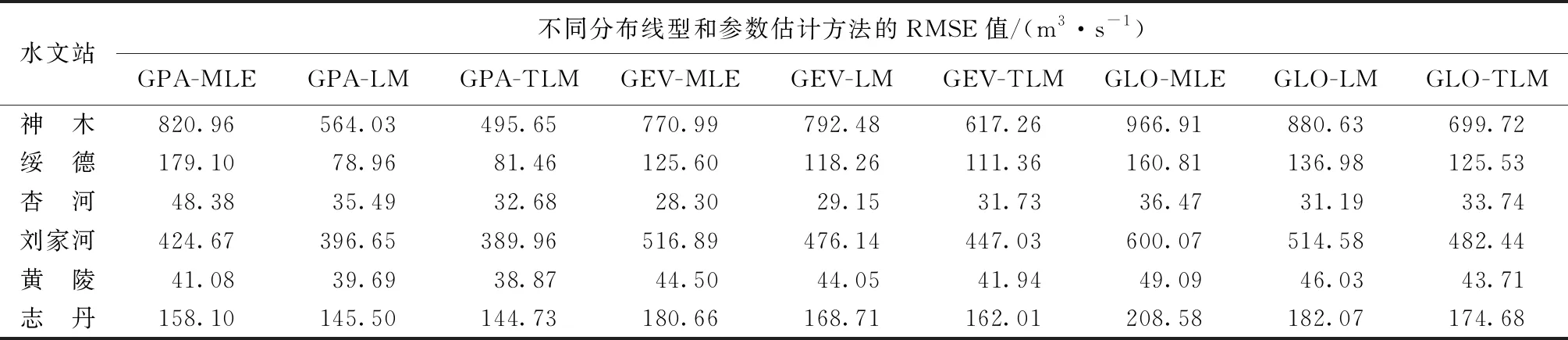
表4 各水文站年最大洪峰流量序列不同参数估计方法RMSE值
由表4结果可知,对6个水文站进行频率分析后,极大似然法对应的RMSE值均大于线性矩法与TL矩法的RMSE值,表明极大似然法的拟合效果劣于线性矩法及TL矩法。同时,线性矩法与TL矩法相比,作为基于线性矩法扩展而来的TL矩法,其对应RMSE值更小,因此两者相比,TL矩法优于线性矩法。
3 结 论
a.选取的3种三参数分布中,杏河站用广义极值分布描述更为合理,而广义Pareto分布能较好地拟合神木、绥德、刘家河、黄陵和志丹5个水文站年最大洪峰流量序列。
b.线性矩法和TL矩法拟合效果优于极大似然法,而线性矩法与TL矩法两者相比,TL矩法表现更优。在对陕北地区的洪水频率分析中,TL矩法是一种可取的、拟合效果合理的参数估计方法。

