考虑提前/拖期风险的第四方物流路径优化问题研究

薄桂华 黄敏 柳欣

0 引言

不确定环境下的路径规划问题,在计算机科学和运筹学中已被广泛地研究,尤其是在不同领域如通信路由和交通工程的应用[1-2]．由于交通网络拥挤、硬件故障、交通拥堵或事故、临时建筑项目和天气条件等因素,使得不确定性无处不在．在配送过程中,因为缺乏及时更新的在线信息(道路状况等),客户将考虑在可能的费用范围内,做出较好的路径选择以规避风险,即在路径选择决策时往往涉及到配送费用和承担风险之间的权衡．

实际配送过程中,客户更希望在某个时间段内接受配送服务,而不是具体时间点．即客户有时间窗口限制,这里的时间窗口限定了配送服务必须在该时间段内完成．如果配送任务提前完成,将可能带来库存成本等费用,增加了配送成本就等于增加了损失而减少了收益,从而带来提前风险,该风险是不容忽视的一个现实情况．如果配送任务延后完成,将降低第四方物流(Forth-Party Logistics,4PL)企业的信誉度,从而带来收益的损失,即带来拖期风险．

陈建清等[3]指出4PL路径优化问题(4PL Routing Optimization Problem,4PLROP)是4PL研究的关键问题之一．4PL供应商不仅要对配送路径进行优化选择,还要对第三方物流(Third-Party Logistics,3PL)供应商进行选择,这样使问题更为复杂,增加了问题求解难度．李秀等[4]把问题分解为路线优化和供应商选择两个子问题,在最短路线计算完成后,再进行供应商选择,这样会带来最优性的损失．此外,该方法在计算配送路线时没有选择供应商,因而在第二阶段很可能受已固定的路线限制,选择到不同的供应商而产生额外的转运费用．Chen等[5]设计了Dijkstra算法和遗传算法求解4PLROP,为4PLROP的研究奠定了基础．Huang等[6-7]给出了4PLROP具体的数学模型,提出了免疫算法和混合免疫算法来求解4PLROP,并验证了算法的有效性．任亮等[8]针对环境的不确定性建立了带有时间窗和随机运输时间4PLROP的机会模型,并采用蚁群算法对模型进行求解,验证了算法的有效性．Tao等[9]从费用折扣角度对4PLROP建立了混合整数规划模型．文献[10-12]分别考虑了带有硬时间窗和软时间窗约束的4PLROP问题,并采用和声搜索对问题进行求解．黄敏等[13]建立考虑单一运输方式的4PL路径优化模型,并根据问题特点设计混合算法对模型进行求解．卢福强等[14]针对物流运输过程中3PL供应商

运输时间和运输成本不确定的问题,基于比例效用理论,建立了考虑客户同时厌恶拖期和超支的4PLROP模型．但是目前大多文献都没有考虑配送时间和转运时间的随机性以及由此带来的不能按期完成配送任务的风险．文献[15]建立了考虑完工风险的4PLROP的相关机会规划模型和相关机会规划等价确定性模型,并设计了遗传算法对问题进行求解．文献[16]引入在险值来刻画及度量拖期风险的大小,建立以最小化拖期风险为目标、配送费用为约束的数学模型，并对问题进行了求解,但是并未考虑提前风险．

本文不仅考虑拖期风险,还考虑提前风险．研究的目的在于如何合理地选择合适的配送方案,使提前和拖期风险在客户可接受范围内的情况下配送费用最小．由此,引入完工概率这一概念,通过令完工时间在时间窗口内实现的概率大于某个置信水平从而给出最优的配送方案．对于风险规避者来说,当然是提前和拖期风险越小越好,等价于完工时间在时间窗口内实现的概率越大越好,即完工概率越大越好．因此,将提前和拖期风险小于某个值的问题转化成完工概率大于某个值的问题．

本文针对带有提前和拖期风险的4PL路径优化问题,建立以最小化配送费用为目标、提前和拖期风险为约束的数学模型,并采用嵌入删除算法的和声搜索算法(Deletion Algorithm Embedded Harmony Search,DA-HS)对问题进行求解,测试不同规模的实例,测试结果表明所提模型和算法是有效的．

1 问题描述

在求解4PL路径优化问题时,4PL供应商不仅要对配送路径进行优化选择,还要对提供配送任务的3PL供应商进行选择．而4PL供应商为客户提供配送方案时,要考虑到配送时间和中转时间的不确定性而导致的提前和拖期风险,对风险进行量化及监控,目标是求得满足提前和拖期风险约束的运输费用最小的配送方案．

将问题用一个多重图G(V,E)描述,其中|V|=n是节点的集合,E是边的集合．如图1所示,图中的s是供应城市,t是需求城市,其他节点是转运城市,它们具有费用、时间属性．由于任意两个城市之间均可能存在多个3PL供应商提供配送服务,故图中任意两点间可能有多条边(每条边代表一个3PL,边上的数字是3PL的编号),每条边都具有费用和时间属性．目标是求得从供应城市到需求城市满足提前和拖期风险约束的费用最小的配送方案．

图1 7节点问题的多重图Fig.1 Multi-graph of seven nodes problem

1.1 变量定义

(1)

(2)

1.2 数学模型

基于以上变量定义,建立如下数学模型:

(3)

(4)

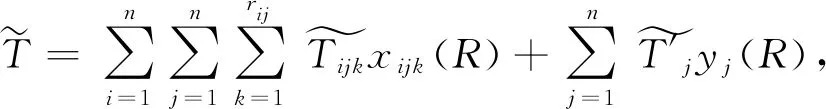
(5)

R={vs,…,vi,k,vj,…,vk}∈G,

(6)

xijk(R),yj(R)∈{0,1}．

(7)

1.3 模型的转化

引理1[17]有限个相互独立的正态分布随机变量的线性组合仍然服从正态分布．

(8)

其中,

(9)

(10)

因此,约束(4)和(5)可以转化成

(11)

(12)

因此,数学模型包括目标函数(3)和约束(12)、(9)、(10)、(6)和(7)．

2 算法设计

本文针对模型的非线性特点和4PLROP问题所特有的特点设计了嵌入删除算法的和声搜索算法(DA-HS)．该算法主要包括编码设计、初始化问题和算法参数、初始化HM、新解的产生、更新HM、终止准则．

主要设计思想[16]是:先在多重图上用HS算法的优化机制产生一个简单图;然后用DA算法在此简单图上求出前K条费用最短路径,DA算法的详细步骤可参考文献[18-19]．由于最优解不一定是某个图上的最短路径,也有可能是次最短路径,因此该算法求前K条最短路径而不是最短路径．

2.1 编码方案

采用以边为基础的整数编码[16]．先将多重图(图1)用邻接矩阵表示,矩阵中的行和列分别代表多重图中的节点,图中有边相连的两节点对应的邻接矩阵元素值为两节点间的边数,即rij;没有边相连时对应的邻接矩阵元素值为0．然后将此邻接矩阵中的上三角非零元素逐行从左到右编码得到一个向量n=[n1n2…ni…nN],其中ni为解向量h的第i个解分量hi的最大取值,N为该问题的编码长度,即解分量的个数．当用解向量h表示简单图时,每个解分量取值为1≤hi≤ni,当用解向量h表示路径时,每个解分量hi可以取零值0≤hi≤ni．

以图1为例,其邻接矩阵如式(13)所示,将矩阵中的上三角非零元素逐行从左到右编码可得7节点问题的向量n=[3 4 2 2 2 3 4 3 2 3 2 2]．由此可知,7节点问题解分量为12个,每个解分量的最大取值分别为3,4,2,2,2,3,4,3,2,3,2,2．

图2给出了解向量h=[3 2 1 1 2 3 2 2 2 1 3 1]所代表的简单图,调用DA算法求得的图 2上的最短路径,即h=[0 2 0 0 0 0 2 0 2 1 0 0]如图2中虚线所示．

0123456 [rij]7×7=01234560340000002220002030400230323020300200420020000000.(13)

图2 简单图及简单图上的路径Fig.2 Simple graph and the route in the simple graph

2.2 初始化问题和算法参数

初始化问题的参数:可允许配送服务完成的最早时间a和最晚时间l、和声记忆库的大小HMS、参数K、和声记忆保留概率HMCR、记忆扰动概率PAR、最大迭代次数NG、置信水平β．

2.3 初始化HM

主要思想:对解向量h的每个解分量hi随机选取1～ni之间的一个整数,即随机产生一个简单图,然后在此图上用DA求出前K条费用最短路径．将满足约束(12)的初始解(路径)存入HM中,直到产生HMS个初始解．其中,HMS与K没有倍数关系．按目标函数值对HM中所有初始解排序．

2.4 产生新解

主要思想:先用HS算法的优化机制产生新的简单图,然后调用DA求出前K条费用最短路径．该算法在每次迭代过程中都产生K个新解,能够在一定程度上加快算法的收敛速度．

由于采用HS来产生新的简单图,因此每个解分量hi只能在0和ni之间取值．为了产生新的简单图,现对每个解分量hi进行如下操作[16]:

1) 生成随机数r1∈(0,1),如果r1

2) 生成随机数r2∈(0,1),如果r2

2.5 更新HM

对新产生的K个新解依次做如下操作:

1) 计算新解目标函数值,判断新解是否满足约束(12),若满足则转下步,否则转3);

2) 根据目标函数值判断新解是否比HM中的最差解要好,若好则用新解替换HM中最差解,否则转下步;

3) 若K个新解都判断完,则更新HM并对HM中所有解排序，否则转1)．

2.6 算法步骤

Step1:初始化算法的参数:可允许服务完成的最早时间a和最晚时间l、HMS、K、HMCR、PAR、NG、置信水平β．

Step2:初始化HM,对HM中所有解(HMS个)按目标函数进行排序．

Step3:产生新解．用HS算法的优化机制生成新的简单图,然后调用DA算法求出前K条费用最短路径．

Step4:更新HM．

Step5:如果迭代次数达到NG,则算法结束并输出最好解，否则转Step3．

3 实验结果与分析

为了验证上述问题的数学模型和算法的有效性,本节测试了5个不同规模的算例．首先,以7节点问题为例,详细描述了算法参数对算法性能的影响并获得一组最佳参数组合．然后,对算法求解不同规模问题的求解质量和效率进行了对比分析．算法采用VC++语言实现,运行环境为Intel(R) Core(TM)i7-2600CPU 3.40 GHz PC台式机．

3.1 参数测试

算法参数的获取是经过大量仿真实验获得的,即当其他参数不变时,测试某一个参数对算法最好率的影响．最好率为算法获得最好解的次数占算法运行总次数的比率．其中,计算最好率时算法运行总次数为100．

图3—7给出了当置信水平β=0.8、时间窗口约束[a,l]=[65,85]时,DA-HS算法求解7节点问题的参数测试过程,其中“最好率”是算法运行100次中求得的最好解的个数与100的比率．仿真实验表明,DA-HS算法最好的参数分别为K=4(图 3),HMS=5(图 4),HMCR=0.8(图 5),PAR=0.25(图6),NG=50(图 7)．

图3 参数K性能分析Fig.3 Performance of parameter K

图4 参数HMS性能分析Fig.4 Performance of parameter HMS

图5 参数HMCR性能分析Fig.5 Performance of parameter HMCR

图6 参数PAR性能分析Fig.6 Performance of parameter PAR

图7 参数NG性能分析Fig.7 Performance of parameter NG

表1给出了DA-HS算法求解7节点问题的结果．由表1可知:当β=0.8、时间窗口约束[a,l]=[65,85]时,算法获得的最好解为95,对应的配送路径为R={vs,2,v2,2,v5,2,v3,1,vt},对应的置信水平为0.867 642,满足约束;当时间窗口约束[a,l]=[70,90]时,算法获得的最好解为93,对应的配送路径为R={vs,4,v2,2,v5,2,v3,1,vt},对应的置信水平为0.814 66,满足约束．当β=0.9、时间窗口约束[a,l]=[65,85]时,算法获得的最好解为96,对应的配送路径为R={vs,2,v2,2,v5,1,v3,1,vt},对应的置信水平为0.904 403,满足约束;当时间窗口约束[a,l]=[70,90]时,算法获得的最好解为96,对应的配送路径为R={vs,2,v2,2,v5,1,v3,1,vt},对应的置信水平为0.927 521,满足约束．由表1中数据还可知：算法的求解时间仅为0.1 s,说明算法的求解速度很快;算法的最好率超过90%,说明算法的稳定性很高．

表1 7节点问题算法的求解结果Table 1 Results of algorithm for solving seven nodes problem

3.2 实例分析

本节分别求解了7,15,30,50和100节点的5个不同规模的算例．其中,50和100节点问题的数据是随机产生的,随机产生数据方法为:将n个节点随机地放在一个a×a的正方形区域内,点(0,0)和(a,a)分别代表初始节点和目的节点,如果两个节点间的欧几里得距离小于等于d,则两节点间有边相连[20],

有边相连的节点间边的个数在闭区间[2,4]中随机生成,边的费用和时间、节点的费用和时间都是随机生成的．其中,50节点算例的a=3,d=0.75;100节点算例的a=4,d=0.7．

表2给出了当置信水平β=0.8时,7,15,30,50和100节点的实例的求解结果．由表2可知,本文设计的算法能够很快地求解不同规模的实例．对于中等规模的问题,如15和30节点的问题,算法的求解时间不到1 s，即使对于大规模问题,如100节点的问题,算法的求解时间仅为1 s,充分说明了算法具有很快的求解速度．算法的最好率都很高,如15节点问题,NG为50时,最好率高达0.98;对于大规模问题,如100节点问题,最好率也高达92%．

表2 当β=0.8时，不同实例的求解结果Table 2 Results of different cases when β=0.8

表3给出了当客户的置信水平β=0.9时,不同算例的求解结果．可以看出算法的求解速度和稳定性都保持很高的水平．本文设计的算法为4PL供应商提供了多种可供选择的配送方案,4PL供应商可以根据客户的不同风险偏好来决策可行的配送方案．

表3 当β=0.9时，不同实例的求解结果Table 3 Results of different cases when β=0.9

4 结论

针对现实配送过程中配送任务既有可能延后完成也可能提前完成,从而带来损失的实际情况,研究了带有提前和拖期风险的4PL路径优化问题．建立了以最小化物流配送费用为优化目标、以提前和拖期风险为约束的数学模型,根据问题的特点,提出了嵌入删除算法的和声搜索算法．通过对5个不同规模的算例的求解结果进行比较分析,表明所提模型和算法是有效的,为带有提前/拖期风险的4PL路径优化问题提供了行之有效的模型和算法．