新疆地区新能源引发次同步振荡典型案例分析

杨志文

(神华国能哈密电厂，新疆 哈密 839000)

当今新能源发电特别是风力发电已经成为中国能源战略的主要组成部分，“十二五”期间，我国在新疆、甘肃、内蒙古、吉林等地规划建设了8个千万千瓦级的风电基地。由于我国能源与负荷中心逆向分布的特点，使得远距离、高容量风电外送成为必然趋势[1]，高压直流输电技术以及串补输电技术是实现大规模风电外送的两种主要方式，但可能导致系统的次同步振荡(SSO)问题[2]，影响外送系统的稳定安全运行。2009年美国德克萨斯州某风场发生的串补电容引起的次同步振荡以及2010年起发生在河北沽原地区风场与串补相互作用引发的次同步谐振事件，使得更多学者认识到风电次同步振荡问题的严重性，开始此类问题的研究[3-7]。

2015年7月1日，新疆哈密地区某电厂三台运行的火电机组全部跳闸(另外一台机组停运)，事故分析表明本次跳闸是由于次同步振荡引起的，这是国内发生的新能源并网引起的新型次同步振荡问题的又一典型案例。

针对本次火电厂发生的新型次同步振荡，本文介绍了跳机电厂次同步振荡事件过程，并基于现场试验和大量监测数据对电厂所在系统的次同步振荡影响因素进行了分析，针对性地提出了抑制本电厂次同步振荡的解决方案，最后对抑制方案的工程可行性进行了验证。

1 某电厂次同步振荡事件分析

新疆哈密地区送出系统结构如图1，哈密地区风、光、火打捆的电源输送基地通过±800kV直流输送至郑州。其中跳机电厂4×660MW机组通过500KV联变送至天山换流站，麻黄沟西风汇444MVA、麻黄沟东风汇643.5MVA通过两级750KV联变与天山换流站相连。

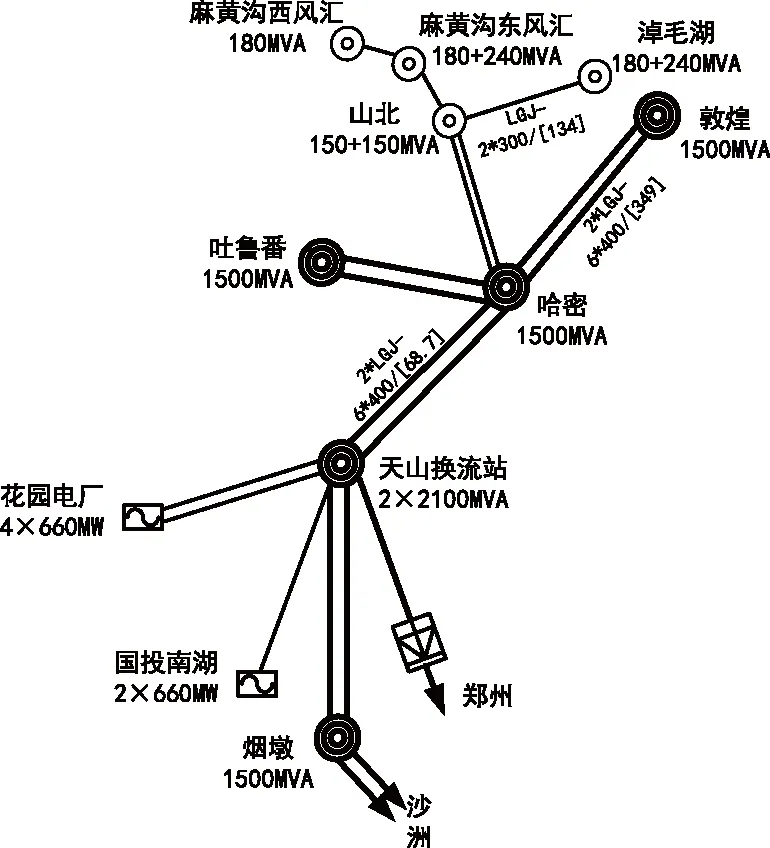
图1 哈密地区送出系统结构图Fig.1 Schematic diagram of Hami area transmission system

2015年7月1日11时53分到55分，某电厂2号、1号、3号机组的轴系扭振保护相继动作跳机，造成损失功率共1280MW，频率波动达0.1 Hz，天中直流功率也由4500MW降到了3000MW。

机组跳闸前，模态3(30.76Hz)扭振峰值达到0.5rad/s，此期间，临近电厂1号、2号机组的轴系扭振保护装置(TSR)发生保护启动(启动模态为模态2，频率为31.25Hz)，且于20秒后保护启动复归。对此期间交流电网PMU记录的次同步范围内的谐波频率分析，交流电网中此时间段内持续存在16Hz到24Hz的次同步间谐波分量，并主要分布于山北站、哈密站、天山站、花园厂、南湖厂沿线。图2为PMU的数据频率波动情况。

图2 PMU数据频率波动趋势图Fig.2 Frequency fluctuation trend chart of PMU data

跳闸机组模态3频率为30.76Hz，其互补频率为19.24Hz(50-30.76=19.24)。根据上图PMU数据频率分布情况，系统谐波频率在10:50左右短时穿越19.24Hz(图2中靠上的水平线)，其后在11:50后持续在19.24Hz波动，对比7月1日跳机电厂TSR记录的模态幅值变化曲线，如图3，机组模态3扭振幅值变大的时间段，与系统振荡频率在19.24Hz附近的时间段完全吻合。

图3 某电厂机组模态3幅值变化曲线Fig.3 Variation curve of mode 3 amplitude a power plant unit

由此，初步判断系统中的次同步振荡谐波是引发此次扭振保护动作的主要原因。

2 某电厂机组扭振特性分析

跳机电厂汽轮发电机组为东汽660MW机组，包括高中压合缸，低压缸A，低压缸B，发电机，集中质量模型参数如下表所示。

表1 机组集中质量模型Tab.1 Lumped mass model of unit

根据厂家提供的机组轴系的连续质量模型，代入多自由度振动微分方程，如公式(1)，获得机组轴系扭转振动的模态频率和振型[8]。

(1)

根据各质量块的转动惯量和扭转刚度可确定出质量矩阵[M]和刚度矩阵[K]，对四质量块模型，M和K阵如下：

(2)

(3)

进一步可求出固有频率和各质量块的扭位移，将扭位移归一化可得到机组的振型曲线。

图4 机组轴系振型曲线 Fig.4 Vibration mode shape curve of unit shaft

机组轴系三阶模态频率分别为15.38Hz、25.27Hz、30.76Hz。根据振型曲线，在发生模态3对应频率的扭振时，各质量块之间的扭位移均较大，更容易引起轴系疲劳损伤，经工程计算，模态3的疲劳累积初值为0.251rad/s，为疲劳累积起始值最低的模态。

跳机电厂机组自2015年3月投运后，数次监测到SSO现象的发生。有的是由于线路电气扰动产生，有的则是由外界激励产生，前者激励后在机组自身的机械阻尼作用下迅速衰减，后者激发后由于线路次同步谐波持续存在，次同步振荡会持续。持续存在的次同步振荡说明某电厂在当前的网络结构下存在严重的次同步振荡风险。

在发生7.1事件跳机前，某电厂配置的TSR装置曾多次启动录波，对录波数据进行分析，发现某电厂机组存在持续振荡甚至呈发散趋势的转速信号，其中幅值较大的为模态3，典型录波曲线如下图所示。

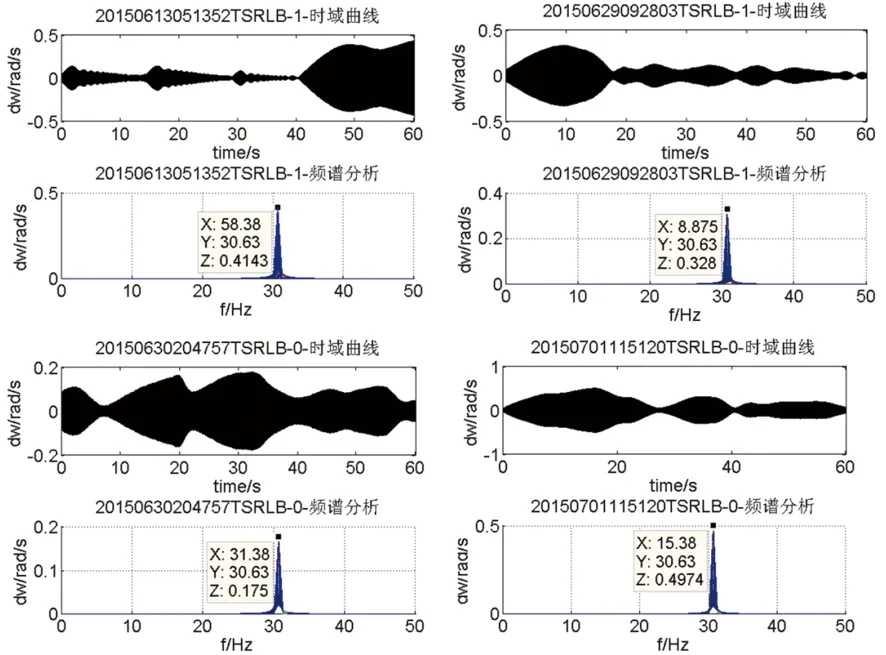
图5 现场录波数据模态3分析Fig.5 Mode 3 analysis of field recording data

分析模态3转速信号幅值及衰减系数，如表1。6月13日05:13:52的录波中(图5中的第一个录波分析图)，模态3衰减系数为负，如表2中加粗斜体所示。

表2 机组录波分析情况汇总Tab.2 Summary of unit wave recording data analysis

当衰减系数大于0时，表示转速信号收敛，阻尼为正；当衰减系数小于0时，表示转速信号发散，阻尼为负。根据以上分析，某电厂机组模态3存在弱阻尼甚至负阻尼的情况，当外界存在次同步频率的谐波扰动且频率与机组轴系频率耦合时，易引起机组扭振，此时轴系存在失稳风险。

3 某电厂次同步振荡扰动源特性分析

跳机电厂由于处于风火打捆并且经直流送出的网架结构内，引起次同步振荡的机理复杂，影响因素较多。自2014年4月以来，无规律发生过百余次的次同步振荡。

风机的转子侧变流器如果控制参数设置不合理可能会引起风电机组次同步扭振[9]，如果风机的并网点电气量中存在间歇波分量，转子变流器回路有可能对该间歇波具有放大作用。

风电场附近装设SVC或SVG[10-11]，由于电力电子器件的快速响应特性，加上控制回路的高放大倍数，SVC与SVG设备会对间谐波分量起到明显的放大作用[12-13]。

跳机电厂距离天中直流47公里，两者之间的电气距离比较近；并且跳机电厂机组与交流电网的联系比较薄弱，仅为两回线路，存在发生次同步振荡发散的可能[14-15]。

为深入分析哈密山北地区风电场功率波动、风电场及汇集站SVG/SVC动态无功补偿设备的投退、功率波动、天中直流功率变化等因素是否对跳机电厂次同步振荡产生影响，开展了风电出力调整、天中直流功率调整、SVC/SVG投退等相关试验。相关试验情况汇总见表3。

表3 哈密地区次同步振荡扰动源特性分析试验Tab.3 Characteristics analysis experiment of SSO disturbance source in Hami area

根据上述试验情况，哈密地区的次同步振荡扰动源可能不止一个，哈密地区的次同步振荡是多种扰动源的综合作用下的结果。

更进一步地采用电磁暂态分析方法表明，影响跳机电厂次同步振荡特性的主要因素及影响趋势为[16-19]：

(1)火电厂机组的运行工况会对次同步振荡的频率和轴系扭振的稳态幅值造成影响，表现为：机械阻尼越小，次同步振荡频率与轴系的固有扭振频率越接近，相互作用引发的扭振强度会增加。

(2)直驱风电机组与交流电网的相互作用可能引起次同步振荡，这一振荡形态受交流电网强度、并网风机台数与出力水平、风机内部控制参数等多重因素影响。

(3)风电场附近装设的SVC或者SVG在恒电压的控制模式下，比例/积分增益越大、阻尼越弱、振荡频率越高时，相比恒无功的控制模式，更容易激发出危险的次同步振荡。

(4)在电厂机组负载水平较低时，临近的特高压直流系统对机组的次同步振荡特性影响相对很小，但是随着负载水平的升高，直流系统对次同步振荡的频率和轴系扭振的幅值的影响增大。

风机变流器或逆变器的控制参数的调整、SVG/SVC等电力电子设备的投退、天中直流的投退、系统运行方式的变化等，引发系统发生次同步振荡时，当系统中谐波电流的振荡频率与发电机组轴系的某一固有扭振频率互补或接近互补时，可能引起机组的扭振保护启动，严重时甚至造成轴系疲劳损伤。

以2016年1月份投运的750kV三塘湖变为例，随着三塘湖地区并网风机数量的增多，系统中频繁发生风电次同步振荡事件。对2016年上半年系统侧发生的次同步振荡情况进行统计，如图6。部分统计数据列于表4。

图6 哈密地区系统侧次同步振荡频率统计Fig.6 Statistics of system side subsynchronous oscillation frequency in Hami area

表4 三塘湖投运后哈密地区次同步振荡汇总Tab.4 Subsynchronous oscillation summary in Hami aera after Santanghu substation commissioning

续表

自三塘湖变投运至7月底，哈密地区共发生66次振荡，振荡频率分布情况如图6。实心正方形标记为系统发生振荡时某电厂TSR扭振保护启动；空心圈圈标记为振荡时某电厂TSR扭振保护未启动。根据统计，某电厂TSR扭振保护启动次数为12次。

根据上述分析结果，哈密地区发生振荡时，在系统侧同时存在次同步频率电流与超同步频率电流，且电流谐波频率不断变化。当电流振荡频率与机组轴系的固有扭振频率互补或接近互补，并且电流的谐波幅值达到一定程度时，就可能引起火电机组侧发生次同步振荡。

4 某电厂次同步振荡抑制方案研究

考虑到实际机网运行方式的多样性和网侧振荡频率的时变性，实际系统中机组扭振的幅值将具有较强的不确定性，因此针对单一振荡因素采取的抑制方法，无法完全解决振荡问题[20-24]。

为了保护机组轴系安全，同时避免火电机组跳机时对系统产生大的冲击，研究在火电机组侧配置次同步振荡抑制措施。参考国内已有成熟的工程实施案例，如上都电厂采取GTSDC+SEDC措施来抑制串补引发的次同步振荡问题，鄂温克电厂采取GTSDC+SEDC措施来抑制呼辽直流引发的次同步振荡问题。考虑到本电厂次同步振荡扰动因素的复杂性，研究采用GTSDC+SEDC联合抑制方案的可行性[25]，此方案的实施为国内外首例抑制新能源引发次同步振荡问题的工程应用。

SEDC采用汽轮机转速信号作为反馈信号，基于分模态原理，通过滤波、比例、移相环节得到各个模态的控制信号，线性相加后通过限幅环节形成SEDC的输出，叠加到励磁调节器的控制信号上，从而在励磁绕组上产生次同步频率电压和电流，进而产生相应的电磁转矩，对SSO起到阻尼作用[26-27]。

GTSDC也以发电机轴系转速偏差信号作为输入量，但不同的是，GTSDC是通过向定子侧注入与扭振模态互补频率的动态补偿电流来增加机组次同步频率阻尼特性，进而达到避免SSO风险的目的[28-30]。

GTSDC+SEDC联合抑制措施示意图如图7所示，两种抑制措施均安装于厂侧，以汽轮发电机转速差作为各自输入，分别输出至励磁侧与定子侧，产生相应电磁转矩，最终生成相应电气阻尼。

图7 GTSDC+SEDC联合抑制示意图Fig.7 Schematic diagram of GTSDC+SEDC combined inhibition

GTSDC+SEDC联合抑制措施使定、转子形成互为备用功能，其中一个装置停运，另一个装置还能继续提供抑制功能，有效降低了发生次同步振荡时的火电机组切机风险。而且二次设备结构简单，相对两个互为备用的一次设备，电厂的投资和运行维护成本都将大大降低。

为验证GTSDC+SEDC抑制方案的有效性，针对电厂实际送出系统进行合理化等值，采用PSCAD软件建模如下拓扑网络模型。图中风电场建模为n台型号相同的1.5MW直驱风机，它们连接于同一条母线上，且控制参数及运行状态一致，相当于实际多风机的平均参数和状态。

图8 等值电网模型Fig.8 Equivalent power grid model

以7.1事件为例，采用GTSDC+SEDC联合抑制方案进行次同步振荡抑制。经仿真分析，加入联合抑制措施后，与无抑制措施相比，模态3转速的稳态振荡幅值从0.197rad/s降低到0.052rad/s，抑制效果达到74%，如图9(a)所示。

同样地，考虑其他恶劣工况，如四台火电机组均为90%出力，机械阻尼较小(满载阻尼的50%)；特高压直流投运；风电场715台直驱风机投运，SVG恒电压控制。在本工况下，采取联合抑制措施，与无抑制措施相比，模态3的最大转速幅值从1.032rad/s减小到0.060rad/s，稳态转速幅值从0.435rad/s降低到0.055rad/s，控制效果达87%，如图9(b)所示。

在上述恶劣四机工况下，更进一步地，发生三相短路故障，此时仿真得到的模态3在有无抑制措施时，转速波形的对比如图9(c)所示。在联合抑制措施下，模态幅值迅速衰减到较低水平。

(a) 7.1事件(a) 7.1 accident

根据上述仿真结果，在火电机组侧安装GTSDC+SEDC装置，模态转速的振荡不再出现大的波动，而是迅速进入平稳期，且振荡幅值大大减小。仿真研究结果表明GTSDC+SEDC抑制方案具有良好的抑制效果。

5 某电厂次同步振荡抑制效果工程验证

某电厂4×660MW机组采用单台机配置GTSDC+SEDC联合方案来抑制次同步振荡。经过严谨的方案对比，采用北京四方继保自动化股份有限公司生产的GTSDC与SEDC装置。本方案于2019年开始工程实施，2020年9月具备投运条件。通过现场试验来验证GTSDC+SEDC的抑制效果。

在机组负荷保持稳定运行工况下，投入SEDC抑制功能，通过GTSDC在电网侧注入谐波电流信号作为扰动源，分别激发出机组侧轴系在三个模式下的扭转振动，激励20秒后，投入GTSDC抑制功能，在SEDC与GTSDC的联合抑制作用下，模态转速信号迅速衰减。模态1、模态2、模态3的抑制效果分别如图10(a)、(b)、(c)所示。

(a)模态1(a)Mode 1

在同样的GTSDC激励条件下，与无抑制措施相比，投入SEDC抑制后，模态1最大转速幅值由无抑制措施的0.225rad/s降低到0.08rad/s左右；激励退出后，在GTSDC与SEDC的联合作用下，模态1的转速由0.08rad/s左右快速降低到0.03rad/s以下；

在同样的GTSDC激励条件下，与无抑制措施相比，投入SEDC抑制后，模态2最大转速幅值由无抑制措施的0.25rad/s降低到0.1 rad/s左右；激励退出后，在GTSDC与SEDC的联合作用下，模态2的转速由0.1rad/s左右快速降低到0.03rad/s以下；

在同样的GTSDC激励条件下，与无抑制措施相比，投入SEDC抑制后，模态3最大转速幅值由无抑制措施的0.22rad/s降低到0.11 rad/s左右；激励退出后，在GTSDC与SEDC的联合作用下，模态3的转速由0.11rad/s左右快速降低到0.03rad/s以下。

投入联合抑制措施后，三个模态的衰减速率与无抑制措施时的衰减速率比较如表5所示。联合抑制措施极大地提高了某电厂机组对三个轴系模态的阻尼能力。

表5 联合抑制下模态衰减系数Tab.5 Mode attenuation coefficient under combined suppression measures

6 结语

某电厂所在的输电网络中存在与机组模态频率互补的振荡电流量是导致某电厂7.1事件轴系扭振跳机的主要原因。哈密地区系统侧频繁发生次同步振荡，当系统中的电气量的振荡频率与机组轴系固有扭振频率互补或接近互补时，有可能引起机组侧扭振保护启动甚至疲劳累计。由于系统侧的次同步振荡扰动因素诸多，仅系统侧的监测抑制措施并不完备。为了保护机组轴系安全，同时避免火电机组跳机对系统产生比较大的冲击，火电机组侧安装GTSDC与SEDC次同步振荡抑制装置，提高阻尼能力，降低切机风险，保护轴系安全。经现场试验验证，在持续激励条件下，投入GTSDC+SEDC联合抑制措施，各模态被激发的转速幅值显著减小，且在激励退出后转速幅值迅速衰减到较小的幅值范围内，模态衰减速率显著提高，GTSDC+SEDC联合抑制效果明显。