考虑梯级水电耦合的水火电系统机组检修计划优化分解方法

代江，田年杰，姜有泉，郑志佳，刘明波，谢敏

(1.贵州电网有限责任公司电力调度控制中心，贵州 贵阳 550000；2.华南理工大学电力学院，广东 广州 510640)

机组检修计划(Generator Maintenance Schedule, GMS)优化是指在满足系统运行和机组特性等约束条件的前提下，确定一定调度周期内机组检修任务开始时间的优化过程[1-2]。根据不同的优化目标，制定得出的检修计划有不同的效果，如提高系统可靠性[3-6]、保证经济效益[7-9]等。而在清洁能源快速发展的背景下，考虑清洁能源的消纳亦成为一种趋势[10]，如文献[11]以最小化弃风量为目标，文献[12]以弃水量最小为目标优化得出检修计划，文献[13-14]综合考虑了新能源的弃置量等。

我国西南地区水资源丰富，含有众多的梯级水电站，梯级水电站之间存在复杂的耦合关系。因此，在建立水火电机组检修计划优化模型时，需要对梯级水电的耦合关系进行合理的描述。文献[15]考虑梯级水电站上下游耦合特性对检修计划的影响，建立了梯级水电站的中长期调度和检修计划双层优化模型。文献[16]以发电收益最大化为目标，建立了梯级水电系统机组检修计划优化的混合整数线性规划(Mixed Integer Linear Programming, MILP)模型，文中结合动态规划、凸包逼近与穷举法对水电站的出力进行了线性化。文献[17]假设水电站出力是发电流量的一次函数，建立了考虑梯级耦合的水火电调度与机组检修计划协调优化MILP模型。

综上，考虑梯级水电耦合的水火电机组检修问题在数学上表现为一个含复杂约束的MILP模型,求解速度有待提高。采用分解法降低问题规模以简化求解是一条有效途径。分解法的基本思想是将原问题分为多个子问题，引入拉格朗日乘子将子问题之间的耦合约束增广到目标函数中，从而将原MILP问题的求解转化为各个子问题的求解。基于模型分解的拉格朗日乘子法的经典算法是拉格朗日松弛(Lagrange Relaxation, LR)法[18-19]。LR主要的缺点是：1)每一次迭代都需要求解所有的子问题以更新乘子，造成拉格朗日乘子出现振荡现象；2)收敛速度较慢，在耦合约束多的情况下甚至难以收敛。增广拉格朗日松弛法(Augmented Language Relaxation, ALR)[20]在目标函数中添加了二次惩罚项以加速收敛，但添加的二次项使得问题不可分。交替方向乘子法(Alternative Direction Multipliers Method, ADMM)[21-22]通过在求解时固定某一子问题的变量解决了这一困难，但无论是ALR还是ADMM，问题的形式都表现为混合整数二次规划问题，其求解效率远低于求解MILP的效率。

近年来，通过代理次梯度法更新拉格朗日乘子的研究日趋成熟[23]。该方法的优势是在每一次迭代中只需求解部分子问题以获得代理次梯度，而不需要求解所有子问题，从而节省计算时间。使用该方法更新拉格朗日乘子，能够保证乘子的变化方向与下降方向构成锐角，即向收敛方向逼近。代理绝对值拉格朗日松弛法(Surrogate Absolute Value Lagrange Relaxation, SAVLR)[24]便是基于以上思想提出，该方法在代理次梯度法的基础上，引入等价于二次惩罚项的线性惩罚项，改善收敛性能，线性惩罚项使得问题仍然保持线性性质，求解速度更快。

本文以最小化火电机组的运行成本、水电机组弃水成本和发电机组检修意愿被调整的成本之和为目标，在满足整个系统、水火电机组、水库及输电线路等的特性和约束条件下，建立考虑梯级水电耦合的水火电机组检修优化MILP模型。再将原问题分解为火电和水电两个MILP子问题，采用SAVLR法求解。并通过两个水火电系统算例验证了算法的有效性。

1 水火电机组检修计划优化模型

水火电系统的机组检修计划优化流程如图1所示。由发电厂申报信息，电力调度中心根据负荷和天然来水的预测，按设定目标进行优化，制定合理的检修开始时间，但不修改检修时长，最后发电厂按电力调度中心下发的检修开始时间安排检修。

图1 水火电系统发电机组检修计划优化的流程图Fig.1 Flow chartof optimizing generator maintenance schedule in a hydrothermal power system

1.1 目标函数

检修计划优化的目标是最小化火电机组的运行成本、水电机组弃水成本和发电机组检修计划调整成本之和为目标，即：

(1)

目标函数包含两项，第一项为火电机组运行成本与弃水成本之和。水电机组在运行时不会消耗燃料，发电成本为零，此处仅考虑火电机组的运行成本，其中Pi,t为第i个火电机组在t时刻的出力，ai、bi和ci分别是对应第i个火电机组成本二次函数的二次项、一次项与常系数；弃水成本即水电站计划外排水的成本，其中ρ为电价，βh为流量—功率转换系数，表示水电站h将流量转化为出力的能力，qh,t为弃水量，表示水电站h当其库容越限时需要排放的水量，该水量不进入水电机组发电，因此会产生相应的损失。

第二项为发电机组检修计划的调整成本。y为检修计划被调整的标志变量，当火电/水电机组i/j申报的检修时间被调整时，yi/yj为1，否则为0；w为惩罚系数，取决于电力调度中心对发电厂满意度的倾向程度。

模型中，T表示检修时段集合，对于年度机组检修计划，本文以天为单位对机组检修计划进行安排，那么T=[1,2……365]；I为火电机组集合；J为水电机组集合；H为水电站集合。

1.2 约束条件

约束条件包括功率平衡约束、火电机组与水电机组出力上下限约束、线路传输容量约束、旋转备用约束、水电站的运行约束、梯级水电站上下游间的水量耦合约束、机组检修的时长约束和连续性约束等。可以概括为三类：系统约束、水文约束及检修约束，具体描述如下。

1.2.1 系统约束

1)功率平衡约束

整个系统的功率平衡约束可描述为：

(2)

其中，Pj,t表示在t时刻水电机组j的出力，J为水电机组数；Dt为系统在t时刻的负荷需求。

2)线路传输容量约束

输电线路传输的功率都不应超过其上限，即：

(3a)

(3b)

其中，αi,l与αj,l为火电机组i与水电机组j对线路l的功率转移因子；αn,l为负荷节点n对线路l的转功率移因子；Dn,t为节点n在t时刻的负荷需求；N为负荷节点集合；Pmaxl,t为线路l的传输容量上限。

3)机组出力约束

(1-xi,t)Pi,min≤Pi,t≤(1-xi,t)Pi,max

(4a)

(1-xj,t)Pj,min≤Pj,t≤(1-xj,t)Pj,max

(4b)

其中，xi,t和xj,t为0-1变量，分别表示火电机组和水电机组的检修状态，为1时机组检修，为0时机组不检修，本文假设机组不检修时处于启动状态；Pi,min与Pi,max表示火电机组的最小和最大出力；Pj,min与Pj,max表示水电机组的最小和最大出力。

4)旋转备用约束

通过预留足够的系统旋转备用容量可以应对负荷预测误差及事故带来的影响，因此，添加旋转备用约束可以保证系统运行的可靠性，即：

(5a)

(5b)

ri+rj=1+r

(5c)

其中，r为备用率。本文中r取为0.05。

1.2.2 水文约束

水文约束是针对水电站的约束，以下约束中，式(6)-(10)是对单个水电站内部变量的约束，式(11)为对上下游梯级水电站变量之间的耦合约束。

1)发电流量约束

0≤uh,t≤uh,max

(6)

其中，uh,t为第h个水电站在t时刻用于发电的水量，称为发电流量；uh,max为第h个水库的最大发电流量。

2)弃水量约束

0≤qh,t≤qh,max

(7)

其中，qh,t为水电站h在t时刻不通过水电机组排放的水量，该水量无法用于发电，称为弃水量；qh,max为其上限。

3)水库容积约束

vh,min≤vh,t≤vh,max

(8)

其中，vh,t为水电站h在t时刻水库的库容；vh,max和vh,min为水库库容的上下限。

4)水电站出力表达式

Ph,t=βhuh,t

(9)

其中，βh为水电站h的流量—功率转换系数，表示将流量转换为出力的能力，该值可利用水电站的历史出力数据和历史发电流量数据拟合得出。

5)水电站出力与机组出力之间的关系

水电站h的出力，等于该水电站内所有水电机组出力之和，如式(10)。

(10)

6)梯级水电站上下游水量耦合约束

上下游水电站之间的水量存在相互影响是梯级水电站一个重要的特点，在建模时需要进行适当考虑。通常在考虑上下游水量时，需要考虑水流滞时的影响，从而使得该式成为复杂的非线性关系式，但在本文中，由于以天为单位，故可以简化对水流滞时的考虑，从而有式(11)。

vh,t-vh,t-1=s(fh,t-uh,t-qh,t+uh-1,t+qh-1,t

(11)

其中，s为将流量转化为体积的系数；fh,t为水电站h处的天然来水，包含降雨和融雪等。

1.2.3 检修约束

1)检修时间约束

(12a)

(12b)

其中，di/dj表示火电/水电机组i/j检修任务的持续时间，所有机组都必须完成规定时长的检修任务。

2)检修连续性约束

对于机组来说，检修任务一旦开始就不能中断，必须确保检修任务的连续性，即：

xi,t-xi,t-1≤xi,t+di-1

(13a)

xj,t-xj,t-1≤xj,t+dj-1

(13b)

3)检修调整变量约束

xi,ei-xi,ei-1≥1-2yi

(14a)

xj,ej-xj,ej-1≥1-2yj

(14b)

其中，ei/ej表示火电/水电机组i/j申报的检修开始时间；yi/yj为0-1变量，表示火电/水电机组的检修调整变量。

以火电机组为例，xi,t与yi,t之间的关系可用表1的真值表表示，若优化得出的检修开始时间不同于申报的时间，则取为1，否则为0。

表1 x与y关系真值表Tab.1 Truth table of x and y

1.3 目标函数的线性化

对于目标函数中的二次项，本小节采用文献[25]中的方法进行线性化，从而使原始模型转化为混合整数线性规划模型。线性化思路如图2所示。

如图2所示，已知火电机组i的最大出力Pi,max和最小出力Pi,min及其发电成本的系数ai、bi和ci，将其发电成本曲线分为两段，其中间值为Pi,mid，分别计算出Pi,min、Pi,mid和Pi,max对应的发电成本Ci,min、Ci,mid和Ci,max后，将Ci,mid与Ci,min和Ci,mid分别连接，得到两条直线(图中红色和蓝色点虚线)，设它们的斜率分别为Ki,1和Ki,2，截距分别为Mi,1和Mi,2，由此可得到发电成本Ci,t线性化后的表达式为：

Ci,t≥Mi,1xi,t+Ki,1Pi,t

(15a)

Ci,t≥Mi,2xi,t+Ki,2Pi,t

(15b)

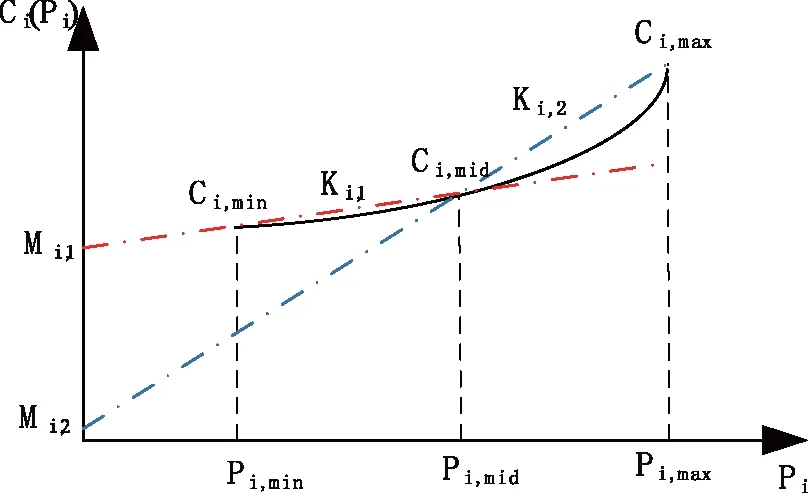
图2 发电成本曲线分段线性化Fig.2 Piecewise linearization of cost curve

通过添加如式(15)的约束，发电成本Ci,t一直在两条直线上方，通过最小化发电成本，可以使发电成本与某条直线上的点重叠，达到将其线性化的目的。若要得到更加精确的逼近效果，可以通过将曲线分为更多段来完成。

(16)

线性化后，使用Ci,t替换(1)中的二次项表达式，可得如式(16)所示的目标函数。至此本文建立了一个水火电机组年度检修计划的MILP模型。

2 水火电机组检修优化分解算法

2.1 模型分解

在求解大规模MILP问题时，可以采用分解的思想，将原问题分解为多个子问题求解，缩小问题规模，从而降低求解难度。对于本文建立的水火电机组检修优化MILP模型，可以十分自然地将其分解为水电和火电两个子问题，即：

火电子问题：

(17a)

s.t. (4a)(5a)(12a)(13a)(14a)(15)

(17b)

水电子问题：

(18a)

s.t. (4b)(5b)(6)-(11)(12b)(13b)(14b)

(18b)

火电子问题与水电子问题之间存在耦合约束如下：

(2)(3a)(5c)

(19)

为简化表达，将火电子问题中的决策变量设为Xa，将水电子问题中的决策变量设为Xb。从而可以将火电子问题采用紧凑形式表示为：

minF(Xa)

(20a)

s.t.Xa∈Ωa

(20b)

类似地，水电子问题可以采用紧凑形式表示为：

minF(Xb)

(21a)

s.t.Xb∈Ωb

(21b)

火电子问题与水电子问题之间的耦合约束采用紧凑形式表示为：

g(Xa,Xb)=0

(22)

其中，式(20a)和式(21a)分别表示火电和水电子问题的目标函数；式(20b)与式(21b)为两个子问题各自内部的约束，仅对属于该子问题的决策变量起约束作用；式(22)为两个子问题之间的耦合约束。

对于水火电机组检修优化问题，耦合约束共有三组，分别是系统功率平衡约束(2)、线路传输容量约束(3a)和备用约束(5c)。对于不等式约束(3a)，需要引入松弛变量将其改写为等式约束：

(23a)

(23b)

其中，zl,t和ul,t为线路传输容量约束的松弛变量，恒大于零。因此，耦合约束(2)、(5c)和(23)就可以写成式(22)表示的等式约束。

2.2 代理绝对值拉格朗日松弛法的应用

通过分解形成的火电子问题和水电子问题，无论在规模上还是在复杂程度上都远小于原问题，易于求解。本节采用代理绝对值拉格朗日松弛法求解。

对于火电子问题(20)，将耦合约束(22)松弛到(20a)中的同时，引入绝对值惩罚项(等价于二次惩罚项)改善收敛性能，则原优化问题(20)转化为：

(24a)

s.t.Xa∈Ωa

(24b)

其中，λ为拉格朗日乘子；γ为恒正罚因子。

在目标函数中引入绝对值惩罚项可以加速收敛，但同样也会使目标函数呈现非线性特征。为解决这一问题，对每一个绝对值引入一个连续变量及两个约束将其线性化，具体形式如下：

(25a)

-om≤gm(Xa,Xb)≤om,m=1……M

(25b)

s.t.Xa∈Ωa

(25c)

其中，om为连续变量；M为耦合约束的数量。

以式(25)方式形成的子问题，在决策变量违反耦合约束时能够给出足够的惩罚，保证了收敛性能；同时也保持线性的性质，从而保证了求解的效率。需要注意的是，在求解火电子问题(25)时，应该固定水电子问题变量Xb；同理，在求解水电子问题时，也应该固定火电子问题变量Xa；而松弛变量在两个子问题的求解中均作为变量进行求解。

在传统的拉格朗日乘子法中，每一次迭代都需要求解所有子问题才能更新拉格朗日乘子。与之不同的是，本文使用的方法使用了代理次梯度的方式，在满足代理最优条件的情况下只需要部分子问题的解就可以更新拉格朗日乘子，并保证更新方向与梯度下降方向成锐角，拉格朗日乘子的更新流程如表2所示。

表2 基于代理次梯度法的拉格朗日乘子更新流程Tab.2 Flow chart of updating Language multipliers based on surrogate sub-gradient method

对于火电子问题，其代理最优条件如下:

(26)

(27)

若求解某子问题后满足代理最优条件，则使用该次迭代中子问题的值更新拉格朗日乘子，拉格朗日乘子更新公式如下：

(28a)

(28b)

(28c)

(28d)

(29)

在本文中，收敛判据ε取10-6。

2.3 算法流程

在求解考虑梯级水电耦合的水火电系统机组检修计划模型时，首先给变量及参数赋初值，并将问题分解为水火电两个子问题，再使用SAVLR法迭代求解。SAVLR法的基本流程与拉格朗日松弛法的类似，均在每次迭代后，判断耦合约束是否满足收敛条件。不同的是在每一次迭代中，SALVR法依次求解2个子问题，若满足代理最优条件(26)则直接利用式(28a)更新拉格朗日乘子；若在该次迭代中完成所有子问题的求解后仍不满足(26)，则需要减小罚系数重新开始该次迭代。分解算法流程如图3所示。

图3 分解算法流程Fig.3 Flow chart of decomposition algorithm

3 算例分析

本节采用3节点6机系统和某省级实际1151节点86机水火电系统为算例验证基于SAVLR法的水火电机组检修优化分解算法的有效性。

3.1 3节点6机水火电系统

在该系统中，节点2接入一个两级的梯级水电站，节点1和3各自接入两台火电机组，该系统发电机特性与水库特性取自某省级实际系统，火电运行成本分两段进行线性化。

算例分别采用SAVLR和ADMM两种方法求解。通过求可行解的方式赋初值，并将分解算法的结果与使用CPLEX求解器直接求解的结果进行对比，如表3所示。

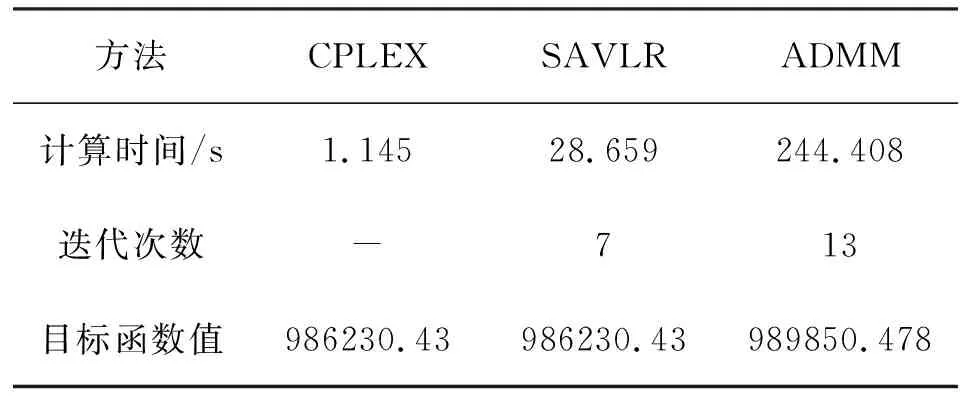
表3 3节点6机系统中采用SAVLR和ADMM获得的结果对比Tab.3 Comparison of results obtained through SAVLR and ADMM in 3-bus and 6-unit system

由表3可以看到，使用SAVLR法，约束被违反时会受到相应的惩罚，且惩罚项为线性形式，使得求解子问题时需要的计算时间较短，最终经过28.659秒，迭代7次后得到的目标函数值为986230.43，与CPLEX直接求解的结果相同。相比之下，ADMM尽管同样对违反约束做出惩罚，但由于问题为混合整数二次规划模型，同时因为每一次迭代中都需要求解所有的子问题，因此需要较长的计算时间，在244秒后经过13次迭代得到的目标函数值为989850.478。

3.2 某省级实际1151节点86机水火电系统

该系统包含621条支路、1151个节点(其中包含202个接负荷的节点)及41台火电机组与45台水电机组。其中拟安排检修任务的有33台火电机组和38台水电机组。该系统有1个梯级流域，其中包含7个干流水电站及2个支流水电站共23台水电机组，该梯级水电站结构如图4所示。年负荷曲线取自该系统真实数据，如图5所示。水火电机组的检修时长均设置为实际检修时长，如表4所示。T表示火电机组，H表示水电机组。

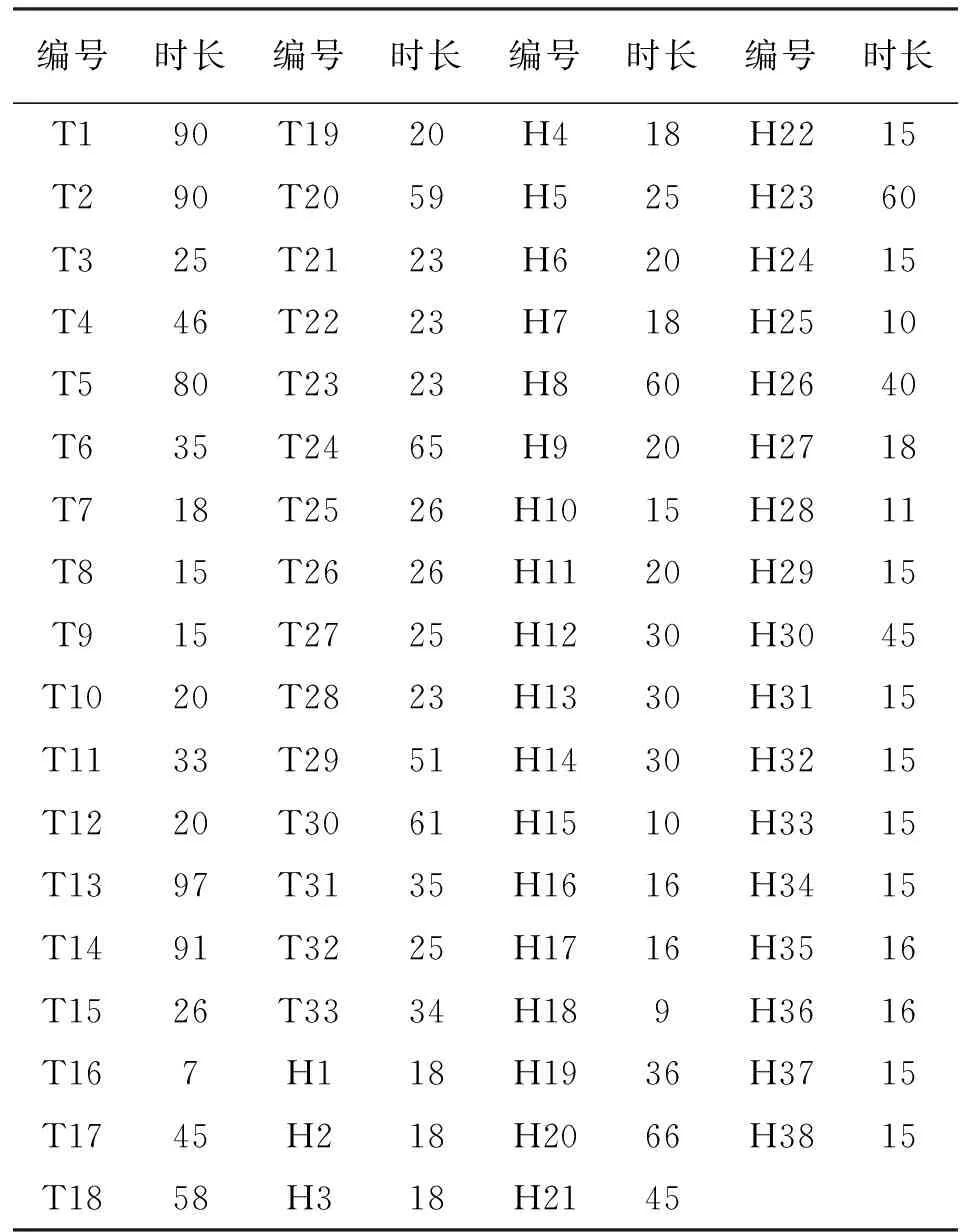
表4 水火电机组检修时长(天)Tab.4 Maintenance time length of hydrothermal units (day)

图4 水电站之间的梯级耦合关系Fig.4 Cascade coupling relationship between hydropower stations

图5 系统年负荷曲线Fig.5 Annual load curve

算例设计为使用SAVLR方法求解与使用CPLEX求解器直接求解时求解结果的对比，以验证SAVLR方法在大规模系统上的适用性与有效性。计算结果如表5。

表5 省级实际水火电1151节点86机系统中采用SAVLR和CPLEX获得的结果对比Tab.5 Comparison of results obtained through SAVLR and CPLEX in real provincial 1151-bus and 86-unit system

由表5可以发现，采用CPLEX求解器直接求解花费的时间为3h34min4s，而使用SAVLR法求解时，若引入的对耦合约束的惩罚项系数γ取20，则计算在4次迭代花费34min56s后收敛，求解结果相对直接求解得到的结果误差约为1.65%，在该次计算中，共求解火电子问题5次，水电子问题3次。而γ取50时，在3次迭代花费23min35s后收敛，相对误差约为4.13%，在该次计算中，共求解火电子问题3次，水电子问题2次。但采用ADMM求解时，迭代过程不收敛。

从求解结果和计算时间可以看到，SAVLR法极大地减少了求解问题所需要的时间，求解得到的结果与直接求解得到的结果偏差不大，证明了SAVLR方法在大规模检修问题上的有效性。同时，子问题计算数量的不同也说明了算法的一个优势，在每次迭代中无须求解所有的子问题以更新拉格朗日乘子，这一点大大减少了计算时间。并且随着γ取值的增大，计算时间和迭代次数会减少，但结果的相对误差同样会有所增大。当然，若γ取得太大则会造成过早收敛，最终结果误差过大的问题，是不可取的。

除了算法的有效性以外，模型的合理性同样需要说明，图6和图7分别为目标函数中w取0时优化得出的水电机组和火电机组的检修计划安排，图中深色块表示检修，浅色块表示不检修，横坐标为日期，纵坐标为机组编号。

图6 火电机组的检修计划Fig.6 Maintenance schedule of thermal units

如图7所示，由于目标函数中考虑了弃水量，优化得出水电机组的检修计划基本上分布在自然来水较为丰富的汛期之外。与此同时，火电机组因为功率平衡及备用约束，检修计划大部分安排在汛期附近，也就是说，火电机组为照顾水电机组在汛期尽量多发满发而检修，水火电机组间的检修计划大致上呈现错峰的特点。

图7 水电机组的检修计划Fig.7 Maintenance schedule of hydro units

以上计算结果均为目标函数中的惩罚系数w设置为0计算得出。以下设置惩罚系数分别为106和206分别进行计算，计算结果如表6所示。

表6 不同惩罚系数下计算结果对比Tab.6 Comparison of results corresponding to different penalty coefficients

表6中，惩罚系数w=0时的计算结果显示，所有机组的检修计划均被调整。而惩罚系数w=106时，检修计划被调整的机组数由w=0时的71台减少到35台，但相应的火电运行成本上升了0.437%，弃水成本上升了5.85%；当w=206时，调整机组数进一步减少到27台，而火电运行成本和弃水成本相较w=0时分别上升了0.912%和8.47%。显然，当惩罚系数w增大时，被调整检修计划的机组数减少，但火电运行成本和弃水成本也会相应地增加。在实际中，电力调度中心可以根据对发电厂满意度的重视程度灵活调整该系数，若设置为0，则求解得出经济性最优的检修计划；若设为较大的值，则以牺牲一些经济性为代价在一定程度上照顾发电厂的检修意愿。

4 结论

本文以天为时间单位，建立了水火电机组年度检修计划MILP模型，综合考虑了水火电机组的运行要求及发电厂的满意度，并且包含了梯级水电耦合及线路传输容量限制等复杂约束。为加快问题求解速度，提出将原问题分解为水电和火电两个子问题，并采用SAVLR法进行求解，该算法具有收敛性能好、计算速度快的优点。

本文基于3节点6机系统算例说明了求解方法的有效性，通过实际1151节点86机系统算例验证了该方法的有效性，为求解大规模机组检修计划优化问题提供了新的求解思路。同时，通过实际系统对建立的模型进行了验证，证明该模型能够合理地安排水火电机组检修任务的开始时间，使水电机组在汛期能够尽量满发；同时，电网公司可通过调整目标函数中第二项系数w的大小来衡量对发电厂检修意愿的倾向程度，具有实际工程价值。