大尺寸固体颗粒提升过程中管道内的固液两相流动特征

宋龙波，滕爽，曹骞，康灿*，丁可金，李长江

(1. 国家泵类产品质量检验中心(山东)，山东 淄博 255209； 2. 江苏大学能源与动力工程学院，江苏 镇江 212013； 3. 中国船舶第七○四研究所，上海 200031)

海底蕴藏着丰富的矿产资源，锰结核存在于4 000～6 000 m的深海，具有极高的开采价值，但从海底将锰结核颗粒提升至水面是海底矿产开发面临的难题.目前，国内外公认管道水力提升是输送海底矿物最有效的方法.锰结核经过初步粉碎后的粒径一般为20～50 mm，然而，学者对于输送固体颗粒大于10.0 mm的介质开展的研究并不多.从输送系统看，其中的管路部分虽然简单，但其放至水面以下，受到水流流动、约束条件、管内介质流动状态等一系列因素的影响，其输送固液混合介质机理性问题有待进一步深入研究.

李秋华等[1]对Y型和U型结构的硬管进行了输送性能的研究，并对比分析了两者各自的优势.在实际的水力提升过程中，管路结构越简单越不易发生堵塞和磨损，但前提是管路的高稳定性.实际运行中，管路输送的是颗粒群，而非单个颗粒，大量的、粒径小的颗粒组成的颗粒群更有利于输送[2].颗粒的运动特征与其速度密切相关，但颗粒速度的测量以及颗粒在两相流体中滑移速度的计算较困难[3]，尤其是目前的光学测量技术在获取大尺寸固体颗粒速度方面仍存在光路遮挡的瓶颈问题.除了管路结构和流动状态，固液两相流动输送的宏观参数也是工程中关注的重点内容，如压降[4]、能量消耗[5]以及决定固相沉积的临界沉积流速等[6].压降与固相颗粒的含量、固体颗粒粒径、管径等密切相关[7]，但目前对压降的预测多依靠经验公式开展，并无更为准确的方法.

计算流体动力学(CFD)方法是解决复杂流动问题的重要手段之一，在固液两相流动的数值模拟方面发挥了重要的作用[8-10].商用CFD软件STAR-CCM+中的离散单元模型(DEM)对管道内大尺寸颗粒固液两相流动进行数值模拟时具有3个优点[11]：一是将颗粒在拉格朗日坐标系下求解，从而可以追踪每个颗粒的位置；二是同时考虑颗粒与液体之间的相间作用力，实现流场和颗粒的双向耦合；三是考虑颗粒之间的相互作用力，从而解释颗粒之间的相互影响.

文中采用CFD软件STAR-CCM+中的离散单元模型(DEM)对管道内大尺寸颗粒固液两相流动进行数值模拟，以大尺寸固体颗粒的水力提升为研究内容，模拟垂直管内的固液两相流动，考虑颗粒尺寸、不同尺寸颗粒的体积比及颗粒形状对输送特征的影响，从而为流动形态判断和稳定性分析提供一定依据.

1 计算模型

1.1 输送速度

定义输送速度为固液两相流体在管道截面上的面积平均速度，其表达式为

(1)

式中：vmix为输送速度；Ql为液体的体积流量；Qs为固体的体积流量；A为管道的截面积.

1.2 输送浓度

定义输送浓度为被输送的固相颗粒体积占固液两相流体体积的百分比，其表达式为

(2)

式中：CV为输送浓度.

1.3 压降数

压降是描述管道输送能力的一个重要参数.为了对比分析数值模拟和试验的结果，定义量纲一的压降数为

(3)

式中：Iv为垂直管道的压降；ρl为液体的密度；g为重力加速度；L为管道的长度.

1.4 CFD-DEM模型

在拉格朗日坐标系中求解颗粒的运动，定位每个颗粒在流场中的位置.在欧拉坐标系框架下对液体的流动进行求解.对于液体和固体颗粒之间的相互作用，通过引入固液两相的体积分数进行考虑.

液相的连续性方程[12]为

(4)

液相的动量方程[13]为

(5)

其中

(6)

式中：ρl为液体的密度；t为时间；εl为液相的体积分数；u为液体的速度；p为液体的静压；μ为液体的动力黏度；Fpl为网格单元内离散相(固相)对连续相(液相)的作用力的总和；ΔVcell为CFD网格单元的体积.

DEM模型基于牛顿运动定律对颗粒运动进行计算，以获得颗粒的速度和位置随时间的变化.单个颗粒的平移运动和旋转运动的方程[14]分别为

(7)

(8)

式中：mi为单个固体颗粒i的质量；vi为颗粒i的平移速度；Fc,ij为颗粒i和颗粒j之间的接触力；Fnc,ik为颗粒i和颗粒j之间的非接触力；Flp,i为流体对颗粒i的作用力；Fg,i为颗粒i受到的体积力；Ii为颗粒i的转动惯量；ωi为颗粒i的旋转速度；Mt,ij为颗粒i和颗粒j之间的切向摩擦力矩；Mr,ij为颗粒i和颗粒j之间的法向摩擦力矩.

1.5 几何模型和边界条件

选用管道材料为碳钢，长度L=3 m，管径D=100 mm，粗糙度100 μm.颗粒为锰结核，球形颗粒的粒径dp=10.0～20.0 mm.混合输送速度vmix=4.0 m/s,固体颗粒体积输送浓度CV=5%.液相模拟采用RNGk-ε湍流模型.设置速度进口以及自由出流边界条件.流体计算域如图1所示，第一层边界层厚度设为10.0 mm，边界层共设4层，延伸率为1.4.采用八面体网格对模型划分，网格单元共81 455个，网格节点共279 082个.

图1 垂直管道的流体计算域

2 试验验证

为了验证所采用的数值模拟方法的可靠性，对垂直管内的固液两相流动进行模拟结果与试验结果的对比.试验结果来自于文献[15]，数值模拟根据该文献中所描述的工况设置了相同的工况参数，所采用的固相输送浓度CV=5%，固体颗粒粒径dp=15.0 mm.数值模拟与试验结果的对比如图2所示.

图2 管道内压降的模拟结果与试验结果对比

由图2可以看出，数值模拟结果与试验值拟合曲线的变化趋势相同，两者的最大误差不超过5%，这表明文中所采用的数值模拟方法是正确的.

3 结果与讨论

3.1 颗粒体积比的影响

在实际的固液两相流体输送过程中，群体固体颗粒的粒径不完全相同，而是分布在一个范围内，所以研究不同尺寸颗粒的体积比对于固液两相流体输送的影响非常重要.以往研究中多假设所有颗粒的尺寸都相同，文中选择3种颗粒粒径(10.0，15.0，20.0 mm)，体积比(V10.0∶V15.0∶V20.0)分别为1∶1∶1，1∶3∶1，1∶6∶1，由此得到3种不同物理性质的固液两相流体.将两相流体的速度vmix统一设为4.0 m/s，输送浓度设为CV=5%.通过数值模拟，获得了不同颗粒体积比时各个尺寸颗粒的平均速度与颗粒直径之间的关系，如图3所示.

图3 不同颗粒体积比时颗粒平均速度与粒径的关系

由图3可以看出：在3种颗粒体积比下，颗粒的平均速度均随颗粒直径的增大而下降，这是由于在密度相同时，较大尺寸颗粒的重量较大，尽管大颗粒的表面积大，其受到的液体的表面力也较大，但这些力不足以使大颗粒保持较高的速度；当dp=15.0 mm颗粒的体积比增大时，另2种颗粒的速度明显下降，而dp=15.0 mm颗粒的平均速度的变化幅度很小；3种不同粒径颗粒造成的压降分别表示为Iv10.0，Iv15.0，Iv20.0,当颗粒输送浓度发生改变时，其对应的压降也随之改变，当dp=15.0 mm颗粒的体积比增大时，Iv15.0增大；当dp=10.0，20.0 mm的颗粒体积比减小时，Iv10.0和Iv20.0降低，故总压降Iv=Iv10.0+Iv15.0+Iv20.0降低.总压降的降低表明作用于颗粒上的压力梯度力变小，导致颗粒的平均速度下降[16-17].

图4为不同颗粒体积比条件下，颗粒的平均滑移速度随颗粒粒径的变化，可以看出：当颗粒体积比V10.0∶V15.0∶V20.0为1∶1∶1时，dp=10.0 mm颗粒和dp=15.0 mm颗粒的平均滑移速度差别不大，而dp=20.0 mm颗粒的平均滑移速度则明显高于其他2种颗粒；当dp=15.0 mm颗粒的体积比增大时，dp=20.0 mm颗粒的平均滑移速度先突降再上升，而最小颗粒，即dp=10.0 mm颗粒的平均滑移速度持续升高，在颗粒体积比为1∶6∶1时，dp=10.0 mm颗粒的平均滑移速度甚至超过了dp=20.0 mm颗粒的平均滑移速度；随着dp=15.0 mm颗粒的体积比的增大，尽管颗粒的平均速度降低，但液体的速度变化很小，大颗粒向液体速度较低的区域聚集，即向管壁聚集，小颗粒向液体速度较高的区域聚集，即向管道中心聚集，这就导致尽管大颗粒和小颗粒的平均速度都减小，但大颗粒的滑移速度降低，而小颗粒的滑移速度升高.

图4 不同颗粒体积比时颗粒平均滑移速度与粒径的关系

取管路沿程中间截面，将其划分为5个区域，如图5所示.

图5 管路沿程中截面区域划分

对5个区域内颗粒的平均速度进行统计，在不同颗粒体积比条件下得到的结果如图6所示.

图6 不同颗粒体积比条件下截面颗粒平均速度分布

由图6可以看出：当dp=15.0 mm颗粒的体积比减小时，颗粒的平均速度沿径向逐渐降低，从区域4到区域5，颗粒的平均速度出现骤降，这是因为壁面处液体的速度最低，颗粒不可避免地受到壁面效应的影响；当dp=15.0 mm颗粒的体积比增大时，每个区域的速度不再呈现单调变化，而是有增有减，且当颗粒的体积比V10.0∶V15.0∶V20.0为1∶6∶1时，除了区域3内的颗粒平均速度较高，其他区域的颗粒平均速度相差不大，这是因为每个区域内都包含大颗粒和小颗粒，大颗粒的速度较低，小颗粒的速度较高，由于大颗粒和小颗粒的分布不均，因此每个区域的整体颗粒速度变化不大.

图7为不同颗粒体积比条件下颗粒的速度分布，可以看出，随着dp=15.0 mm颗粒的体积比增大，颗粒的整体速度下降，高速度的小颗粒明显减少.dp=15.0 mm颗粒的增大导致了总压降的减小，进而使作用在颗粒上的压力梯度力减小，所以降低了颗粒的速度.在该3种工况下，小颗粒的速度普遍较高，分布更加均匀，而大颗粒的速度普遍较低，容易发生堆积现象.

图7 不同颗粒体积比时颗粒速度分布

3.2 颗粒形状的影响

为研究颗粒形状对垂直管内固液两相流动状态的影响，采用文献[18]中的方法对颗粒的形状系数SF进行定义，即

(9)

式中：a，b，c为相互垂直的3条轴的长度，其中c为最短轴的长度.

在保证颗粒体积相等的情况下，设计了2种不同于球体的颗粒，通过小颗粒填充的方法，建立如图8所示的非球形颗粒，其形状系数SF分别为0.54和0.76.当球体颗粒的形状系数为1.00时，粒径为15.0 mm.

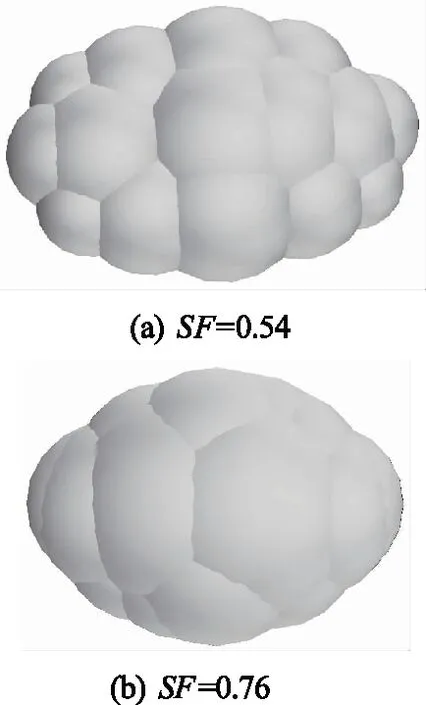
图8 非球形颗粒几何模型

颗粒平均速度与形状系数的关系如图9所示，可以看出，当形状系数为1.00时，颗粒的平均速度最高，表明此时固液两相流体的输送性能最好；当颗粒的形状系数减小时，颗粒的平均速度先降低后增大，说明颗粒几何形状的改变使其所受的形状阻力也发生了变化.

图9 颗粒平均速度与形状系数的关系

颗粒受力面积的变化与颗粒的运动学特征相关，所以群体颗粒的输送状态也随颗粒形状系数变化而变化.当形状系数较小时，颗粒的受力面积较小，颗粒受到的驱动力较小，所以颗粒速度较低.

颗粒的平均滑移速度与形状系数的关系如图10所示，可以看出，当形状系数为1.00时，颗粒的平均滑移速度最小.

图10 颗粒平均滑移速度随形状系数的变化

与球形颗粒相比，形状系数的减小会增加颗粒的滑移速度.然而，颗粒的平均滑移速度与颗粒的形状系数之间并不存在单调关系，这与固体颗粒在液流中运动时沿流动方向的投影面积有关.当投影面积增大时，颗粒受到的驱动力增加，颗粒的平均速度升高，反之亦然.

图11为管段截面上的颗粒平均速度分布，可以看出：对于球形颗粒，每个区域内的颗粒平均速度分布都较为均匀；从区域1到区域5，颗粒的平均速度逐渐下降，但下降幅度不大；对于形状系数较小的颗粒，其平均速度与径向距离之间并不呈线性关系，较为明显的趋势是，在区域1—4内，颗粒的平均速度相差并不大，但从区域4到区域5，颗粒的平均速度急剧下降；相比于球形颗粒，形状系数较小的颗粒受到的壁面效应更加严重，更容易在壁面处发生速度骤降.

图11 截面上颗粒平均速度的分布

图12为不同形状系数时颗粒速度的空间分布，可以看出：球形颗粒的整体速度最高，当形状系数为0.54时，会出现一些速度较高的颗粒；当形状系数为0.76时，颗粒的速度最低，球形颗粒的受力面积最大，驱动力最大，故颗粒的平均速度最大；形状系数为0.54和0.76的颗粒在运动过程中，颗粒呈倾斜状态向前运动，但形状系数为0.54的颗粒倾斜角度较形状系数为0.76的颗粒大，所以其在运动方向上的受力面积较大，故而其平均速度也较高；在靠近壁面处，形状系数为1.00的颗粒速度最高，而其他2种颗粒的速度较低，这与图11所示的速度分布相对应.

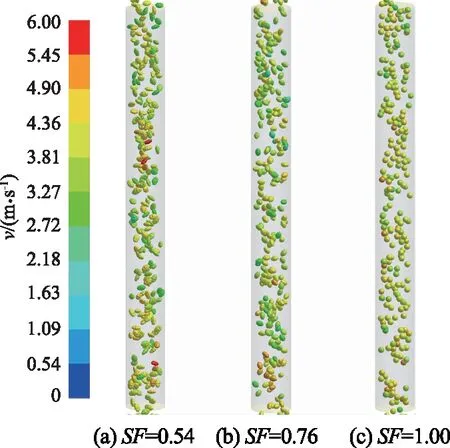
图12 不同形状系数时颗粒速度分布

4 结 论

1) 颗粒体积比的改变会对颗粒速度及其空间分布产生影响.粒径为15.0 mm颗粒的体积比增大会导致另2种颗粒的平均速度下降.

2) 球形固体颗粒的输送性能最好，颗粒的平均速度最高，颗粒的滑移速度最低，在管段截面上，颗粒的速度分布较为均匀.

3) 颗粒形状系数的改变会导致颗粒的平均速度下降和平均滑移速度上升，同时，管壁处颗粒速度明显降低.