一类扰动五次哈密顿系统的极限环分支

何 青，张景涛，洪晓春

(云南财经大学 统计与数学学院,昆明 650221)

希尔伯特第16问题是当今数学界研究的热点问题之一.为了解决这一问题,俄罗斯数学家V.I.Arnold在1977年提出了弱化的希尔伯特第16问题,即研究Abel积分孤立零点个数的最小上界问题.其中,由于Lienard系统能够模拟电台和真空管道的震动,受到了国内外学者的广泛关注.对于扰动的Lienard系统:

其中0<|ε|≪1,Rm(x)和Rn(x)分别是关于x的m和n次多项式.

如果ε=0,当m<4时,系统(1)称为椭圆哈密顿系统,当m≥4时,系统(1)称为超椭圆哈密顿系统.近年来,超椭圆哈密顿系统受到了极大的关注.

洪晓春[1]研究了系统:

使用判定函数方法证明了系统(2)有3个极限环,并且进行了数值模拟.

王彦杰等[2]研究了系统:

在(a0+a1x+a2x2+a4x4)y扰动下的极限环分支情况,得出扰动系统有5个极限环,并使用数值探测法给出了5个极限环的具体位置.

对于扰动的四次系统:

王彦杰等[3]使用判定函数及数值模拟的方法得出系统(4)有3个极限环.

对于扰动的五次系统:

王彦杰等[4]使用判定函数及数值模拟的方法得出系统(5)有3个极限环.

赵丽琴[5]讨论了系统:

在3个参数组合下有界周期环上阿贝尔积分的孤立零点个数问题.其中,P(x)=a0+a1x+a2x2+a3x3+a4x4.

对于五次哈密顿系统:

赵丽琴等[6]对系统(7)的相图情况进行了分类，分为a,b,c,d,e,f,g七种情况，并且证明了系统(7)在任意n次多项式扰动下的极限环个数不超过54n-13.

的极限环分支情况,得出系统(8)有3个极限环,并且给出了出现双尖点极限环的情况.

继续使用判定函数方法[8]及数值探测方法[9]对系统(9)进行研究,得出系统(9)有4个极限环,并且使用数值模拟方法对分析结果进行了检验，给出了极限环的具体位置.

使用符号((n1,n2),n3)表示左边小区域内的极限环个数是n1,右边小区域内的极限环个数是n2,外面大区域内的极限环个数是n3.本研究得出的结果是：系统(9)有4个极限环，而且4个极限环的情况具有2种分布形式,分布形式为((2,0),2)和((0,2),2).

1 非扰动系统的定性分析

考虑系统(9)的非扰动系统:

系统(10)是一个超椭圆哈密顿系统,且哈密顿函数为

2x6-6x4+3x2-6h=0.

(12)

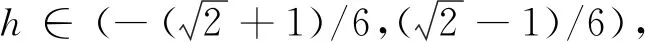
哈密顿系统(10)的相图如图1所示.

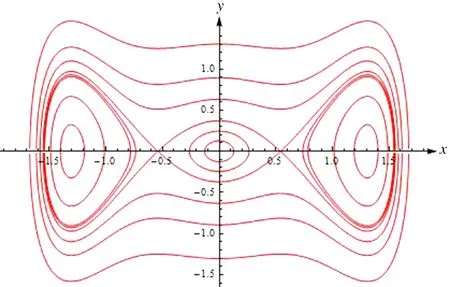
图1 哈密顿系统(10)的相图

2 扰动系统的判定函数及极限环

考虑扰动系统(9),由文献[10]的有关定理，可得其阿贝尔积分如下：

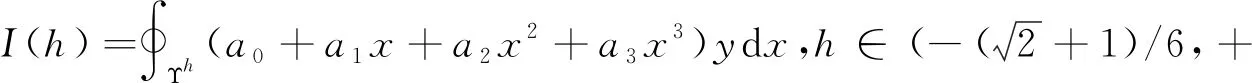
(13)

对式(13),运用格林公式得

(14)

其中，Υh(D)表示由闭轨道Υh所围的内部区域.

令I(h)=0,得出:

(15)

由式(15)得下列判定函数:

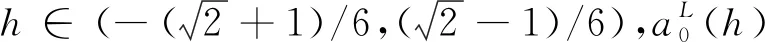
当a1=1.32,a2=-1.41,a3=-1.26时,由判定函数(16)～(19)得判定函数如表1及表2.再由判定函数表1及表2得到判断曲线如图2.

表1 当a1=1.32,a2=-1.41,a3=-1.26时,系统(9)左、右两区域的判定函数

表2 当a1=1.32,a2=-1.41,a3=-1.26时，系统(9)内、外区域的判定函数

由系统(9)的判定曲线图2，使用文献[2]的命题1，可得到以下结论.

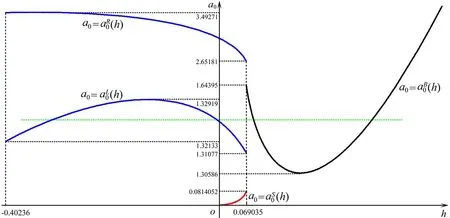
图2 当a1=1.32,a2=-1.41,a3=-1.26时,系统(9)的判定曲线

定理1对于系统(9)，如果a1=1.32,a2=-1.41,a3=-1.26,0<ε≪1,而且:

1) 当0

2) 当1.305 86

3) 当1.310 77≤a0(h)≤1.321 33,或a0(h)=1.329 19时,系统(9)有3个极限环；

4) 当1.321 33

图3 当a1=1.32,a2=-1.41,a3=-1.26,a0=1.328,ε=0.001时,系统(9)的4个极限环

对于系统(9)，取a0=1.328,a1=1.32,a2=-1.41,a3=-1.26,ε=0.001,使用文献[9]的方法进行了数值模拟，获得了图3中的4个极限环,分布形式为((2,0),2),其中,外面的两个大极限环分别过点(0,1.442 1)和(0,0.793 8),左边的两个小极限环分别过点(-0.852 1,0)和(-1.038 5,0),4个极限环的稳定性情况是:从外到内顺次为稳定的、不稳定的、不稳定的、稳定的.

再由判定函数的奇偶性及积分区域的对称性,可以得出系统(9)的4个极限环情况，还有((0,2),2)分布形式.

3 结论

使用判定函数方法[8]，借助于数值计算方法研究了系统(9)的极限环分支情况.研究表明,当a1=1.32,a2=-1.41,a3=-1.26,以及0<|ε|≪1时,由判定曲线得出,系统(9)可以分支出4个极限环,分布形式为((2,0),2).当a1=1.32,a2=-1.41,a3=-1.26,a0=1.328,ε=0.001时,使用数值探测方法[9]对所得结论进行了检验，并且给出了4个极限环的具体位置.再由判定函数的奇偶性及积分区域的对称性,得出系统(9)的4个极限环情况具有((2,0),2)和((0,2),2)二种分布形式.

以上内容为纯理论研究,对于许多实际问题，若研究的系统能够出现稳定极限环，这是一种非常好的性态，例如，在生物数学中，研究人员也研究这一类极限环的存在问题,见文献[11-13]等.