考虑换乘紧张度的登机口分配优化建模
薛清文,郎 洪,王勇智,陆 键
(同济大学a.道路与交通工程教育部重点实验室;b.数学科学学院,上海 201804)
近年来,急剧增长的客、货运输量对民航运输需求不断增加。部分机场现有的航站楼旅客流量已达到饱和状态,机场通过增建新的航站楼缓解原有航站楼登机口不足的问题。但对于部分中转旅客而言,会增加其在转场过程中的换乘时间,大大降低旅客对于航空公司和机场的服务满意度。如何在实现登机口资源利用最大化的同时,提高中转旅客效率已成为改善枢纽机场中转运行效率的关键性问题。
针对登机口分配问题,国内外部分研究学者分别进行如下研究:以登机口空闲时间最小[1]、分配到同一登机口的前后航班冲突概率最小[2]等为目标建立单目标多约束的登机口指派模型进行研究;从场面运行效率的角度出发,建立以航班延误最小[3]、飞机滑行距离最小[4],航班分配效率最高[5]等优化模型;从旅客角度出发,以旅客步行距离最小[6]为目标进行优化。部分研究中,旅客步行距离分别与远机位使用数量[7-8]、航班分配效率[9]、登机口鲁棒性[10]及登机口空闲时间[11]等目标相结合,实现多目标的优化建模。
纵观国内外研究现状不难看出,尽管已取得了较多研究成果,但大部分研究成果集中于登机口指派效率等方面,以航站楼内始发旅客的步行距离为研究对象,并没有充分考虑中转旅客在不同登机口之间的中转时间和换乘紧张度。目前,针对中转旅客换乘问题的登机口优化分配建模研究尚不多。针对旅客换乘的模型中主要以中转旅客的换乘时间、换乘舒适度、跨机场换乘的旅客总人数最少等为目标进行优化[12-13]。这些研究中,对于旅客换乘紧张度的研究较少。因此,分别以总换乘紧张度最小、航班分配失败率最低及登机口使用数量最少为目标,建立中转旅客登机口分配优化模型,并利用生物地理学优化(BBO,biogeographybased optimization)[14-16]算法对模型进行优化求解,从而降低中转旅客的换乘紧张度,提高多航站楼登机口指派效率。
1 模型建立
1.1 问题描述
针对多航站楼的机场运行导致中转旅客换乘时间延长的现状,研究以中转旅客总换乘紧张度最小、航班分配失败率最低及登机口使用数量最少为目标的航班-登机口分配问题。在提高场面登机口运行效率的同时,缓解中转旅客的换乘紧张。
1.2 模型假设
针对模型进行如下假设:①航班时间均为国际标准时间;②以换乘旅客为研究对象,不考虑始发旅客和终到旅客;③航班的实际到达时间、实际出发时间与航班计划一致,受天气状况、管制等其他突发因素干扰较小;④研究时段内的所有航班信息和旅客中转信息是已知的;⑤旅客中转过程中的换乘时间与登机口位置有关,即流程、捷运及步行时间是相对固定的,不考虑人为随机因素的影响;⑥登机口指派是一个连续过程,选择一段时间内的航班进行指派。
1.3 登机口分配优化建模
建立了旅客换乘连接变量,引入“换乘紧张度”参量来评价登机口分配对旅客换乘时间的影响。模型首先最小化中转旅客的总换乘紧张度,其次确定航班分配失败率最低,尽可能多地将航班分配到合适的登机口;在此基础上最小化登机口的使用数量。具体建模过程如下。
1.3.1 目标函数
中转旅客在中转过程中会受到换乘时间的限制。定义“换乘紧张度”为中转旅客的换乘时间与航班连接时间的比值。总换乘紧张度即单个旅客的换乘紧张度乘以中转旅客数量。在登机口分配的过程中,需最小化中转旅客的总换乘紧张度。
假设gk、gm为中转旅客到达登机口和出发登机口,gk,gm∈G,G为登机口集合。换乘旅客在中转过程中需在登机口gk和gm之间经过相关登机流程、捷运及步行。为登机口gk和gm间中转旅客的最短流程时间,包括安全检查、办理中转手续等为登机口gk和gm间中转旅客的捷运时间,即当登机口所在的航站楼不同时,需要搭乘捷运的时间为登机口gk和gm间中转旅客的步行时间。流程时间、捷运时间和步行时间都与登机口gk、gm所在的航站楼及功能属性有关。定义该旅客的换乘时间为。
假设fi为到达航班,fj为出发航班,fi,fj∈F,F为航班集合。afi为航班fi到达时刻,dfj为航班fj出发时刻,航班连接时间为dfj-afi。
换乘紧张度表示如下
式中

为使中转旅客的总换乘紧张度最小,建立目标函数1,即
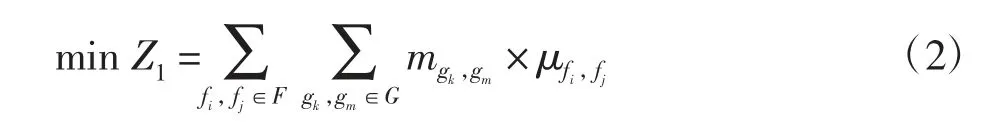
式中mgk,gm为登机口gk和gm间的中转旅客数量。
根据式(1)和式(2)可知,首先确定每个航班分配到与其属性相符的登机口,进而判断到达航班fi与出发航班fj之间是否存在中转旅客。如果存在中转旅客,则进一步确定两个航班所分配到的登机口位置,根据登机口所在的区域确定两个登机口之间的最短流程时间、捷运时间和步行时间,即获得中转旅客的中转时间;根据机票信息确定中转旅客的航班连接时间及中转旅客数量,进而得到中转旅客的总换乘紧张度。标函数Z1使得中转旅客的总换乘紧张度最小。
其次,在登机口指派的过程中,应将尽可能多的航班分配到登机口,可建立目标函数2,即

式中:m为待分配航班的总数量;为出发航班fi成功分配到登机口gk的航班数量。目标函数Z2表示航班分配失败率最低,即航班分配到合适登机口的数量最大。
最后,最小化登机口的使用数量,提高场面资源的运行效率,建立目标函数3,即

式中zgk为决策变量,用于判断登机口gk是否被使用。在满足航班与登机口功能属性相符的基础上,尽可能将航班分配到同一登机口,从而最小化登机口的使用数量。
1.3.2 约束条件
根据登机口分配规则,建立如下约束条件。
1)机体类型匹配约束
飞机的机体类型相匹配时,航班fi才能分配到登机口gk。航班机体型号Cfi和登机口机体型号Cgk分为

故有机体类型匹配约束为

2)到达航班类型匹配约束

故有约束为
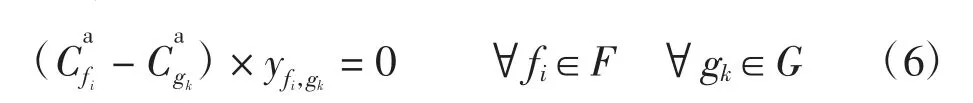
3)出发航班类型匹配约束
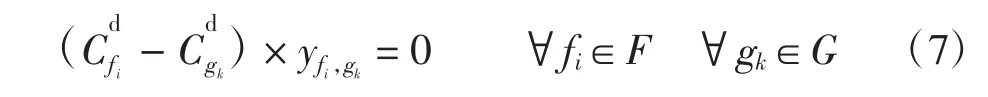
4)飞机指派约束
转场飞机的到达和出发两个航班必须分配到同一登机口,即一个飞机(用其所承运的航班fi替代)只能分配到同一登机口,不能同时分配到多个登机口或转移登机口,故有约束为

5)登机口指派约束
确保分配到同一登机口的两个航班占用登机口的时间段无重合,afi、dfi为航班fi到达、出发时刻,afj、dfj为航班fj到达、出发时刻,故有约束为
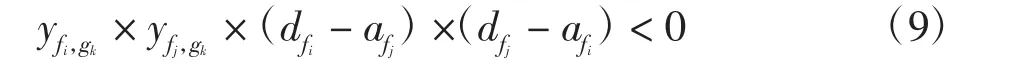
6)空档间隔约束
分配到同一登机口的两个航班应满足一定的空档间隔时间,T为同一登机口两航班之间的空档时间45 min,故有约束为

式中M为一个足够大的值,保证式(10)成立。
7)飞机及机位编号正整数约束
i,j,k∈Z+(11)
综上所述,建立如下的多目标多约束登机口分配优化模型为
2 模型求解
登机口分配是一个非线性动态规划问题,含有多个约束条件,该问题的优化常使用整数规划算法求解[17-19],部分研究采用启发式算法[20-22],包括蚁群算法、粒子群算法(PSO,particle swarm optimization)等,但这些算法存在运行时间长,且对初始种群依赖性较高的问题,因此,提出基于BBO 来求解该问题。BBO 是基于生物地理学理论的新型智能优化算法,具有良好的收敛性和稳定性[14-16]。该算法通常用适应度指数(HSI,habitat suitability index)来描述一个栖息地的种群丰富度,一个栖息地所包含的种群数量与HSI 成正相关。该算法的流程图如图1所示。

图1 BBO 算法流程图Fig.1 The flow chart of the BBO algorithm
模型求解的流程如下:
步骤1将飞机的到达航班类型、出发航班类型、飞机机体类型等信息与登机口到达类型、出发类型、登机口机体类型一一对应,为每架飞机筛选出属性匹配的登机口;
步骤2随机将飞机分配给属性匹配的登机口,确定每个登机口的开放时间,即该登机口前序飞机的出发航班时刻,同时满足45 min 的空档间隔时间;与未分配登机口的飞机的到达航班时刻相比较,满足要求即可分配给该登机口,否则拒绝分配,搜索其他可分配登机口;从而生成初始可行解,完成登机口初始分配;
步骤3根据旅客的到达航班和出发航班的飞机转场记录号,确定飞机分配到的登机口编号,进而判断登机口所属终端厅区域;计算每位中转旅客的最短流程时间、捷运时间及步行时间,进而确定旅客的换乘时间;
步骤4根据旅客转场记录号、中转旅客的航班连接时间和换乘时间,计算总换乘紧张度;
步骤5对步骤2 生成的初始可行解进行有效评估,将步骤3 和步骤4 计算结果代入目标函数Z1、Z2和Z3计算适应度函数,并在定义的种群数量范围内进行登机口分配结果更新;
步骤6利用BBO 优化种群所有解,在满足约束条件的基础上对登机口分配多次迭代,经过多次迁移和突变操作,用上代最优值替换本代最差值,与当前最优解结果比较,判断是否更优;
步骤7判断是否满足迭代次数,输出当前最优解。
3 仿真验证
以国内某大型机场的航站楼(T)和卫星厅(S)登机口结构作为研究对象,T 和S 示意图如图2所示。T和S 统称为终端厅,有捷运线相通,可以快速往来运送国内、国际旅客。
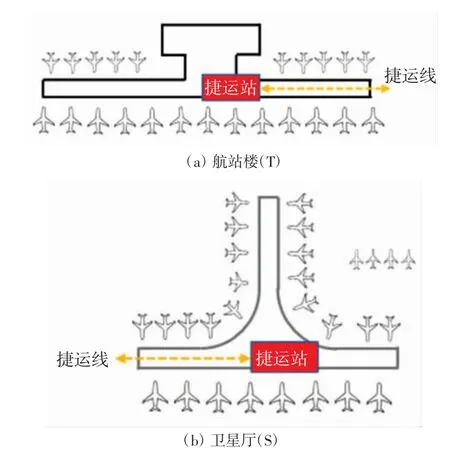
图2 国内某大型机场的航站楼(T)和卫星厅(S)的设计Fig.2 The design of the terminals T and S at one airport in China
航站楼有28 个登机口,卫星厅有41 个登机口。部分登机口配置数据如表1所示。航站楼的登机口分布在North、Center 和South 共3 个区域,卫星厅的登机口分布在North、Center、South 和East 共4 个区域;登机口的出发航班和到达航班类型分为国际航班(I)和国内航班(D);机体类型分为窄体机(N)和宽体机(W)。
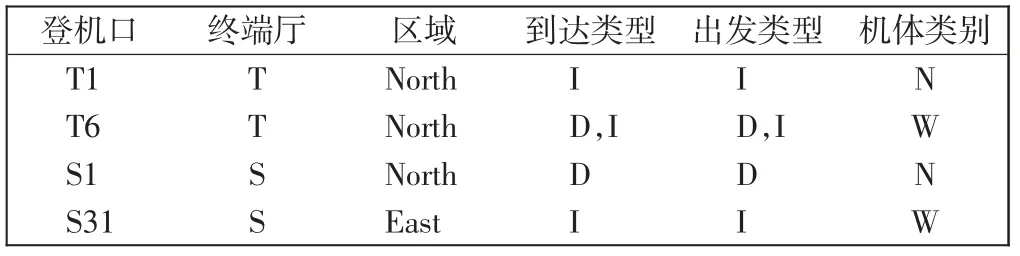
表1 国内某大型机场的航站楼登机口配置数据Tab.1 The configuration data of gates at one airport in China
选择该机场在2018年1月19日的飞机转场计划和中转旅客信息进行模型的仿真验证。转场飞机共606 架次,飞机转场计划部分如表2所示。中转旅客共2 751 人,部分旅客中转信息如表3所示。
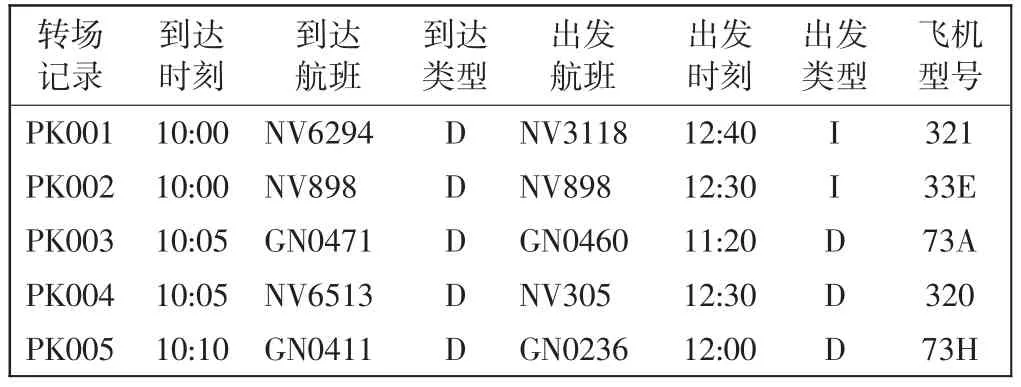
表2 国内某大型机场的飞机转场计划Tab.2 The transit record of aircrafts at one airport in China

表3 国内某大型机场的旅客中转信息Tab.3 The information of transit passengers at one airport in China
中转旅客从前序航班的到达至后序航班的出发之间的流程,按D、I、T、S 组合成16 种不同的场景。这些场景的最短流程时间和乘坐捷运次数如表4所示。假定旅客无需等待,随时可以发车,单程捷运时间为8 min。换乘旅客的步行时间与登机口所在区域有关,如表5所示。
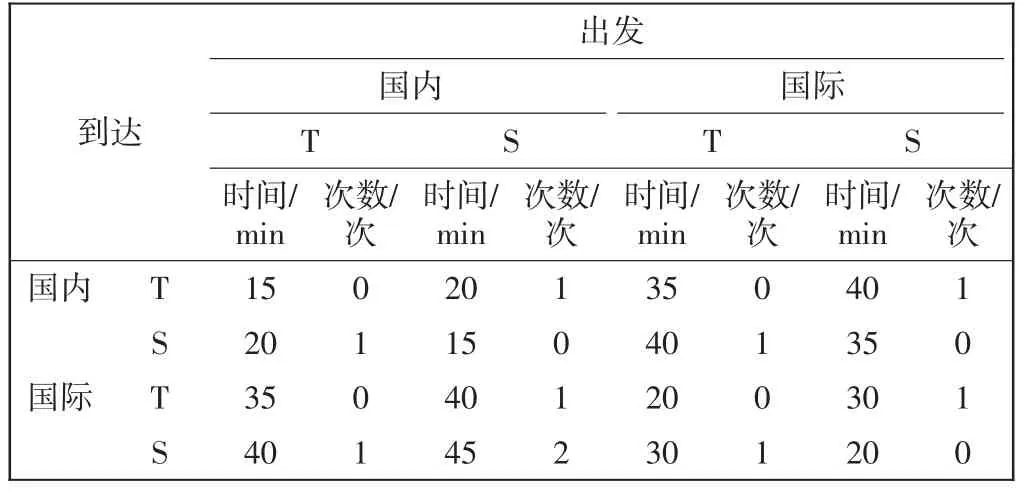
表4 换乘旅客的中转流程时间和捷运次数Tab.4 The process time and metro rides of transit passengers
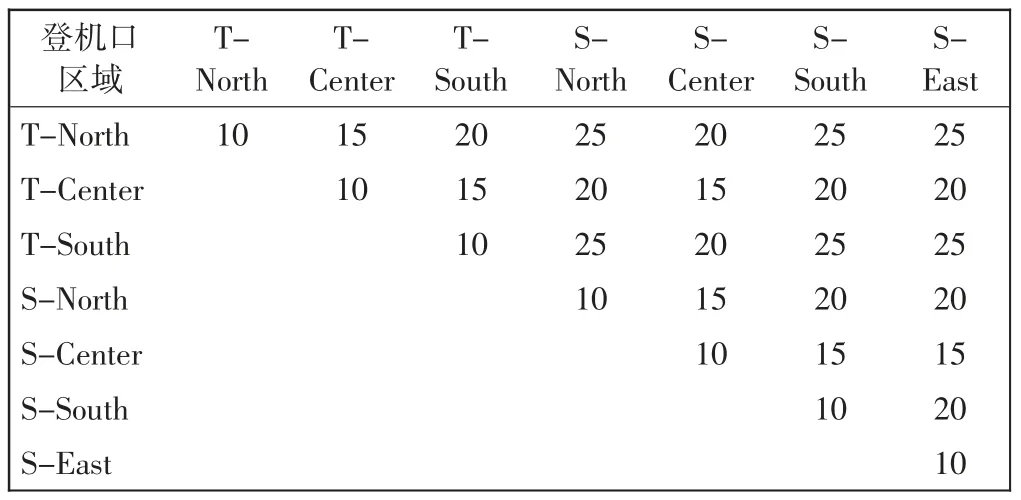
表5 换乘旅客的步行时间Tab.5 The walking time of transit passengers min
3.1 适应度函数收敛
运用C 语言编程求解多目标多约束的登机口分配优化问题,在求解过程中分别以Z2+Z3及Z1+Z2+Z3为目标函数进行优化,对比分析旅客换乘紧张度对于登机口分配的影响。其最优解的迭代进化过程如图3所示。
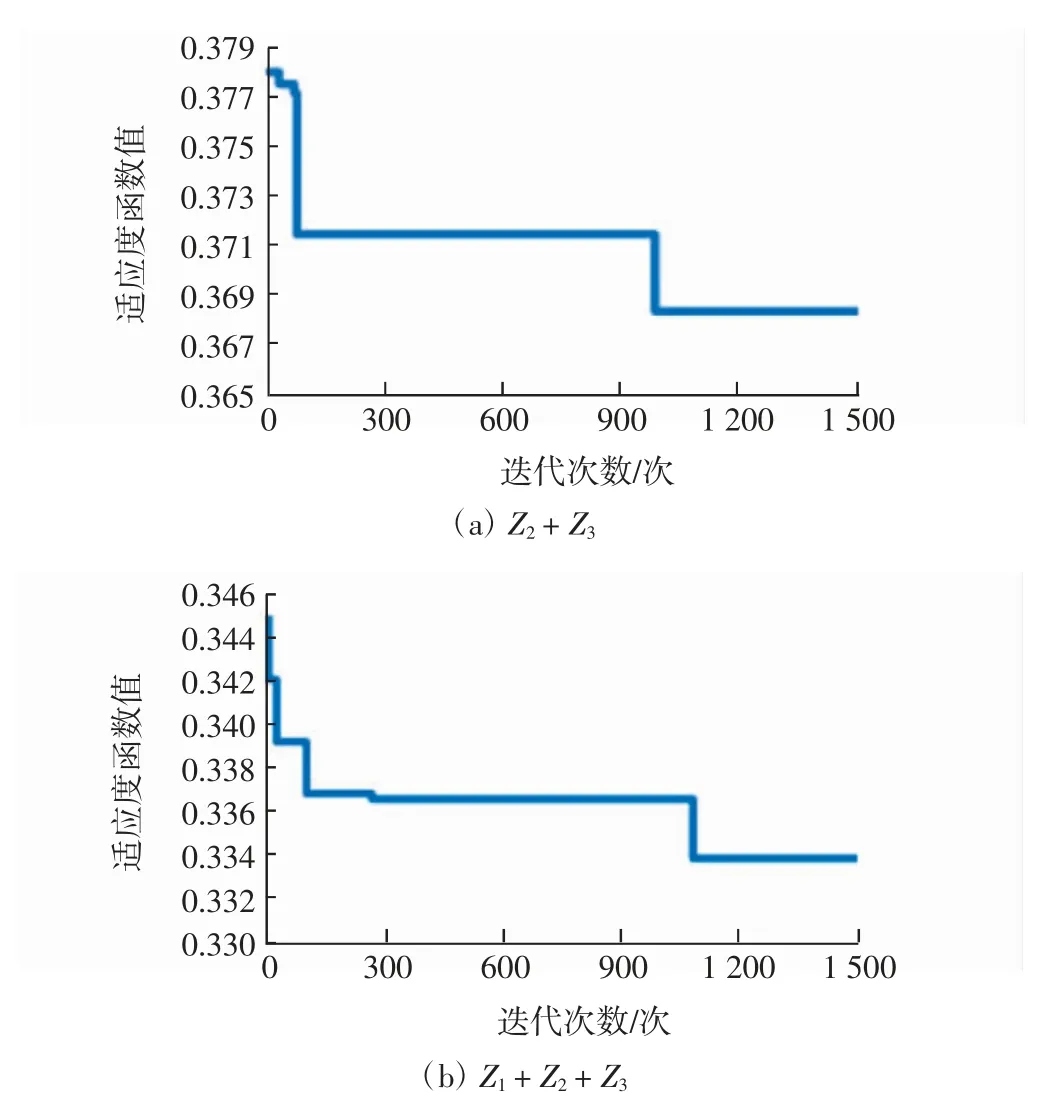
图3 模型最优解迭代进化过程Fig.3 The evolution of the optimal solution of the model iterative
在目标函数优化的过程中,首先会根据登机口分配的约束条件随机分配,然后通过BBO 的迁移和突变操作改变登机口分配的结果,并不断优化目标函数,使其函数值不断减小。当迭代次数达到85 次时,适应度函数的收敛速度最快,在1 000 次附近,适应度函数进一步收敛。
3.2 中转旅客换乘紧张度分析
登机口分配优化模型的仿真结果与采用相同数据的航班先到先服务(FCFS,first come first served)调度结果相比较。在FCFS、Z2+Z3及Z1+Z2+Z3的优化结果中,中转旅客的换乘时间分布和换乘紧张度分布如图4 和图5所示。
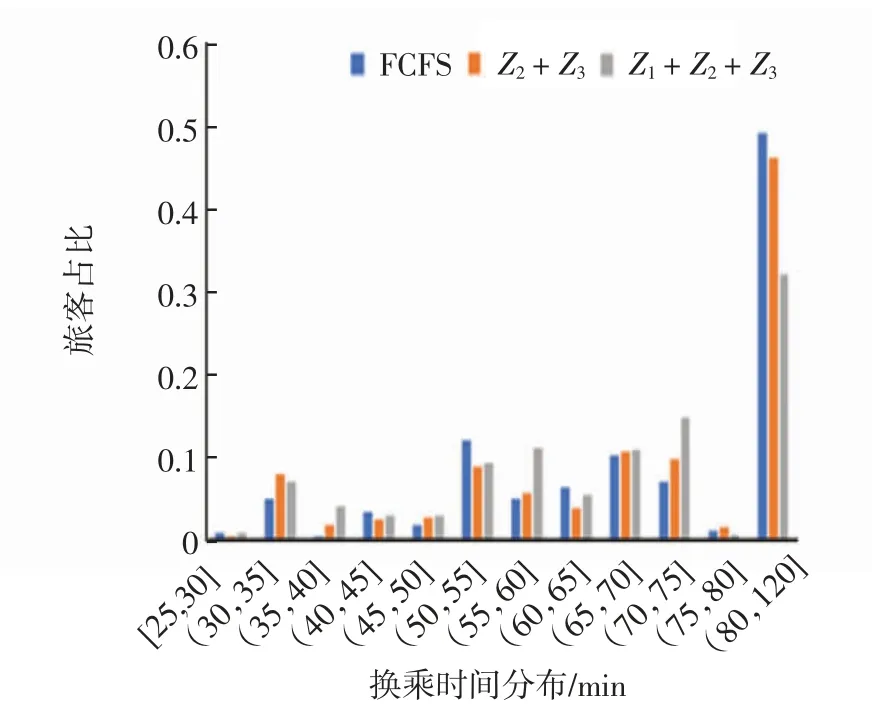
图4 旅客换乘时间分布Fig.4 The distribution of transfer time for passengers
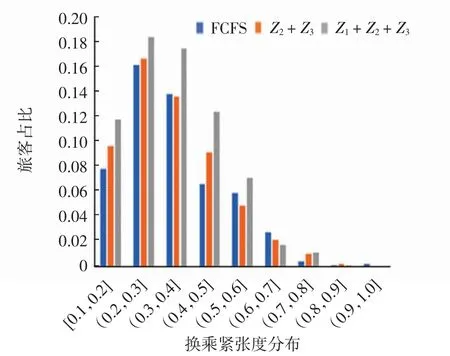
图5 旅客换乘紧张度分布Fig.5 The distribution of transit tension for passengers
由图4 和图5 可知,换乘时间在80 min 以内的旅客中,换乘时间在50 ~75 min 内的人数相对较多。旅客的换乘紧张度在0.1 ~0.5 之间的比例较大,其他区间较小。在FCFS 的分配结果中,45 min 内成功换乘的旅客比例为9%;54%的旅客换乘紧张度在1.0 之内。在基于目标函数Z2+Z3的分配结果中,45 min 内成功换乘的旅客比例为12%;58%的旅客换乘紧张度在1.0之内,相比于FCFS 提高了4%。在基于目标函数Z1+Z2+Z3的分配结果中,45 min 内成功换乘的旅客比例为15%,70%的旅客换乘紧张度在1.0 之内,相比于FCFS提高了16%。在登机口分配优化建模中,考虑中转旅客的换乘紧张度,不仅降低了中转旅客的换乘时间和换乘紧张度,而且增加了中转旅客的换乘成功率,提高了中转旅客的服务效率。
3.3 登机口分配结果对比分析
登机口分配优化模型的仿真结果与采用相同数据的FCFS 调度结果相比较,对比分析如表6~表8所示。
表6~表8的数据结果显示,在登机口分配过程中,基于FCFS 的航班分配成功数量为448 架次,登机口使用数量69 个,其中T 和S 的登机口平均使用率分别为73.46%和38.61%,成功换乘人数1 487 人,总换乘紧张度为3 474。基于目标函数Z2+Z3成功分配航班498 架次,提高了11%;登机口使用65 个,且登机口的平均使用率增加,说明提高了登机口的使用效率;成功换乘1 588 人,总换乘紧张度为3 288,相比于FCFS 降低了5%。基于目标函数Z1+Z2+Z3成功分配航班进一步增加至502 架次,相比于FCFS 分配结果提高了12%;宽体机分配成功率为100%;登机口使用66个,登机口的平均使用率较高;成功换乘人数1 936人,相比于FCFS 增加了30%,总换乘紧张度最低为2 622,相比于FCFS 降低了25%。相比于前两种模型,第3 种模型能够降低航班分配失败率,显著减少旅客的换乘时间和换乘紧张度,且登机口的使用效率较高,更加符合登机口分配的需求。
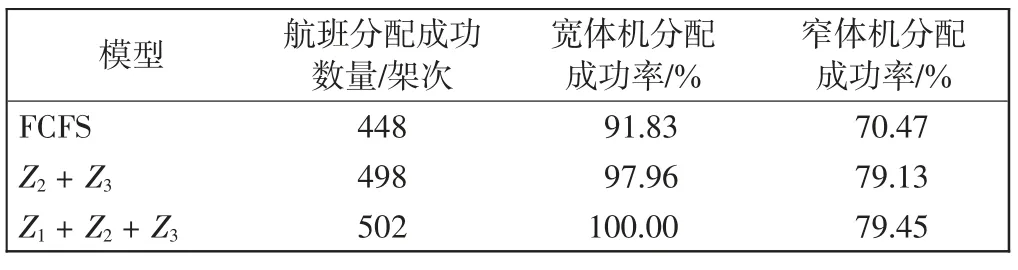
表6 中转航班的分配结果Tab.6 The assignment results of transit flights

表7 航站楼T 和S 的登机口使用结果Tab.7 The assignment results of flights at terminal T and S
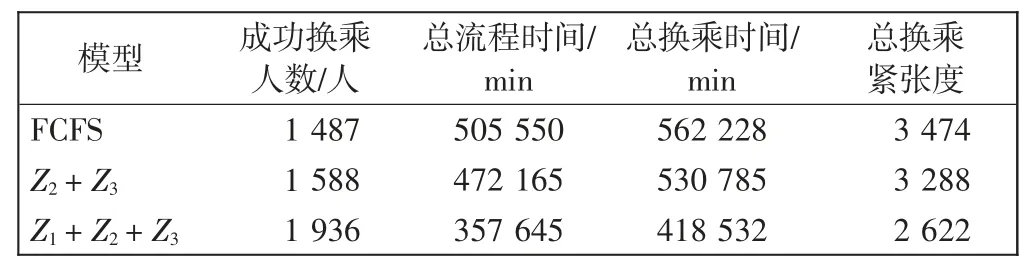
表8 中转旅客的换乘情况Tab.8 The transfer results of transit passengers
4 结语
(1)考虑中转旅客在换乘过程中的中转时间建立了“换乘紧张度”的参量,评价登机口分配对于中转旅客的影响程度。以中转旅客总换乘紧张度最小、航班分配失败率最低及登机口使用数量最少为目标,同时考虑航班分配的登机口类型约束、航班冲突约束等条件,建立多目标多约束的登机口分配优化模型。
(2)采用BBO 对模型进行仿真验证,计算效率较高。模型算法的求解速度和效率及收敛性受种群数量和变异概率影响较大,一般而言,种群数量越大,求解成功的概率也越大。但过高的种群数量会大大增加计算时间。
(3)模型可使更多的旅客在换乘成功的同时,换乘紧张度降低,在保证场面资源利用效率的同时,提高旅客的服务满意度。
考虑中转旅客的换乘紧张度在登机口分配优化方面的研究目前非常少,下一步的研究工作是将该方法推广到航空器场面运行和航站楼设计的联合应用中,探讨不同智能算法求解的优劣性。

