耦合模块度优化与谱聚类的供水管网分区算法

杨之江，周煜岷，扈 震，曾 文，周 扬，李晓丽，冯 丽

（1.中国地质大学（武汉）地理与信息工程学院，湖北武汉 430078；2.武汉众智鸿图科技有限公司，湖北武汉 430074）

在城市化发展进程中，供水管网漏损率居高不下，管理难度越来越大。科学合理地划分独立计量分区（district metering area，DMA）对供水管网漏损控制至关重要［1］。近年来，许多学者研究并提出多种基于网络拓扑的供水管网分区优化方法，模块度优化和谱聚类算法是其中2种主流的方法，在供水管网分区中得到了广泛应用［2］。

在基于模块度优化的管网分区方法中，Diao等［3］利用快速模块度优化算法对供水管网进行社区结构划分，证明了该算法用于供水管网分区的有效性；Liu等［4］分别采用快速模块度优化、随机游走和Metis算法对案例管网进行分区实验，相比随机游走和Metis方法，验证快速模块度优化算法能得到高模块度的分区方案；在基于谱聚类的管网分区方法中，Herrera等［5］利用谱聚类算法，以管径和标高差作为边的权值，构建相似度矩阵，将相似度高的节点划分到同一分区；Nardo等［6］运用加权谱聚类算法，考虑管网几何和水力特性，确定了管网最优分区布局。快速模块度优化算法（Fastgreedy）相比谱聚类算法（Spectral Clustering，SC），虽然能生成较高模块度的分区结果，但也会产生更多的边界管道，而SC能约束边界管道数量，但在模块度方面表现一般。通过这2种分区算法所得到的分区方案在综合模块度和边界管道数均衡性方面表现较差，更重要的是它们在对供水管网分区时，会产生狭长型无效分区（同一分区边界线部分重叠，成线状向外突出的区域），不便于分区管理。此外，水力特征是影响管网分区有效性的重要因素之一，分区不可避免地会增加管网水头损失［6］，同时管网的铺设以街区为最小单元不断扩展，形成商业、工业、居住等功能分区，最后形成的管网空间布局会带有明显的中心性、空间分异性［7］。Yao等［8］指出地区功能区特征由其所提供的基础设施服务所表征，可以用区域内部各类兴趣点分布（points of interest，POIs）来描述。而Fast-greedy和SC本身没有考虑管网的水力特征和空间布局。

本文研究耦合模块度优化与谱聚类的供水管网分区算法（coupling modularity optimization and spectral clustering algorithm，MOSC）。该算法结合管网水力特征和空间布局，对中国某市供水管网分区，以模块度和边界管道数为指标，构建MOSC与Fast-greedy、SC对比实验，验证MOSC有效性。

1 快速模块度优化和谱聚类算法

1.1 快速模块度优化算法

模块度Q是衡量网络划分为社区的强度指标，以Q值的大小来评价社区划分的优劣，Q值越接近1时，表示对社区结构的划分越好；模块度Q值越大，社区内部连接越紧密，社区间连接越稀疏，分区效果越好［9］。基于模块度Q最大化的快速模块度优化算法是一种自下而上的贪婪优化算法，该算法基于贪心算法的思想，从每个节点为一个社区开始，依次合并相邻的社区计算产生的模块度变化量ΔQ，沿着模块度Q增加最大的方向不断合并社区，直到获得模块度Q最大所对应的社区划分结果［10］。模块度Q计算公式可表示为

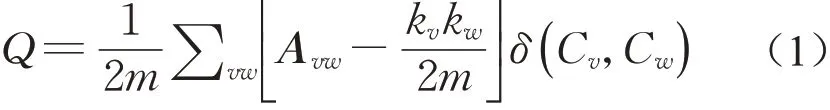
式中：A为网络的邻接矩阵，v和w为节点，若节点v和节点w相连，则A vw=1，否则A vw=0。m为网络的边数，kv，kw分别为节点v、w的度，即连接到节点v、w的边数。Cv为节点v所在的社区。若节点v和节点w在同一社区，则Cv=Cw，δ=1，否则δ=0。

1.2 谱聚类算法

边界管道是指连接不同管网分区之间的管道，由于供水管网分区方案是通过在边界管道上安装流量计和闸阀来实现，它的数量决定了分区改造的经济成本，所以从经济成本角度，边界管道数量越少越好［11］。在边界管道数量上表现优异的谱聚类算法建立在图论中的谱图划分理论基础上，是一种基于两点间相似关系的聚类算法，其本质是将聚类问题转化为图的最优划分问题［12］。该算法利用特征值和特征向量挖掘管网的社区结构，得到的聚类结果中社区内部相似度高，社区间相似度低且规模相似。该算法的最大特点是能使分割的边界管道数量少［13］。此方法的具体步骤为［2，14］：

（1）计算图的拉普拉斯（Laplacian）矩阵

式中：A为邻接矩阵；D为对角矩阵（也称度矩阵），对角线上的值为节点的度，为节点i与节点j之间的权重。

（2）拉普拉斯矩阵L标准化为

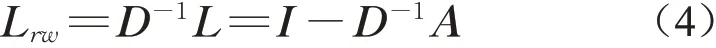
（3）计算L rw的特征值与特征向量。Luxburg［15］指出求解图的拉普拉斯矩阵的零特征值对应特征向量个数等于图的连通分量个数。更进一步，将特征值从小到大排序取前k个较小特征值构成的谱空间中，拓扑联系紧密，相似性权重高的节点处于一个区域，而拓扑联系稀疏相似性较低的样本对则处于不同的区域，从而实现样本在高维空间中的线性可分。故按特征值从小到大取前k个特征向量组成矩阵X=[x1，x2，…，x k]∈Rn×k，取矩阵X的行向量，得到矩阵Y，将矩阵Y的每一行作为Rk空间中的一点y。

（4）利用K-means算法对Rk空间中的每一点y进行聚类，得到最终的聚类结果。

2 MOSC与评价指标

2.1 MOSC

针对Fast-greedy和SC的不足，MOSC耦合Fast-greedy和SC，一方面，集成Fast-greedy对网络拓扑紧密连接结构的高模块度社区挖掘能力，另一方面，集成SC对边界管道数量的约束能力，并综合考虑管网的水力特征和空间布局。MOSC包含3个步骤：最优模块度求解、对偶图构建和拉普拉斯特征分解与聚类，如图1所示。

图1 MOSC流程图Fig.1 Flowchart of MOSC

2.1.1 最优模块度求解

城市供水管网是由相互连接的管道和其他附属设施组成的设施网络，水通过这些管道以及附属设施输送到需水节点，以满足系统的用水需求和压力要求［16］。在管网无向无权图G=(V，E)中，以取水点、水表、阀门等作为节点，V={v1，v2，…，vn}为节点集，vi∈V，i=1，2，…，n为管网节点，以相邻节点之间的管道作为边，E={e1，e2，…，em}为边集，ej=(vj1，vj2)，ej∈E，j=1，2，…，m为管段。最优模块度求解的具体步骤为：

（1）利用Fast-greedy对图G进行社区划分，初始化每个节点为一个社区，初始条件下的社区划分结果为C0={c1，c2，…，cn}，ci为第i个节点所在的社区，此时，vi∈ci，i=1，2，…，n，计算初始化条件下的模块度Qt0。

（2）遍历图G所有连边，分别合并相邻2个社区，得到每一种合并方案并计算对应的模块度Qt1，对比初始状态下的模块度Qt0。得到模块度变化量

式中：Qt0为当前社区合并条件下的管网模块度；Qt1为合并2个社区之后的模块度。

（3）取合并后ΔQ最大的合并方案为新的社区划分方案，划分后的结果为C1={c1，c2，…，cn−1}，其中c1，c2，…，cn−1为划分后的社区。

（4）重复上述社区合并过程，当Q最大时，停止合并，得到对应的社区划分结果C={c1，c2，…，cl}，其中c1，c2，…，cl为最终社区。

2.1.2 对偶图构建

基于社区划分结果，结合社区内部的水力特征与空间分布特征来描述社区，完成对偶图的构建。如图2所示，图中ci为第i个社区，w ij为社区i与社区j之间的权重，i，j=1，2，…，7。

图2 社区划分对偶图Fig.2 Duality map of community division

社区划分对偶图的具体构建步骤为：

（1）以社区划分结果为基础，将社区作为节点，社区之间的连接关系作为边，构建社区划分对偶图G′=(V′，E′)，其 中V′=C={c1，c2，…，cl}为 节 点集，cx∈V′，x=1，2，…，l为 对 偶 图 节 点，E′={e′1，e′2，…，ez′}为边集，e′y=(cy1，cy2)，e′y∈E′，cy1≠cy2，y=1，2，…，z为对偶图边。

（2）为了降低水头损失，得到对管网水力性能影响最小的分区布局，提出以下水力特征向量Hd

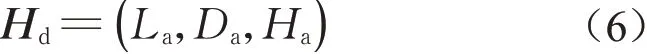
式中：La为社区内平均管径；Da为社区内平均管长；Ha为社区内平均节点高程。

（3）提出以餐饮、购物、医疗服务、住宿、政府机关、休闲娱乐、交通出行和科研教育8个类型的POIs数量来表征社区内部的空间区位特征，得到以下功能结构特征向量Fc：

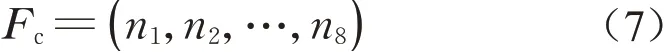
式中：n1，n2，…，n8分别表示餐饮、购物等8个类型的POIs数量。

（4）拼接水力特征向量和功能结构特征向量得到总的特征向量

式中：x i为第i个节点对应社区的总特征向量；nij为第i个节点对应社区的第j种类型的POIs数量。

（5）对每个特征向量进行标准化zi=(ti−μ)/σ，其中，zi为x i中各个特征向量标准化后的特征值，ti为x i中的各个特征向量的特征值，μ为所有x i中各个特征向量特征值的均值，σ为所有x i中各个特征向量特征值的标准差。计算各个社区之间标准化后的特征向量欧氏距离d ij=‖ ‖x i−x j，变化得到相似性作为边权重

式中：std(d ij)为d ij的标准差。

2.1.3 拉普拉斯特征分解与聚类

基于构建的对偶图G′=(V′，E′)，利用SC，通过拉普拉斯特征分解和K-means聚类，得到管网分区结果。具体分区步骤为：

（1）计算对偶图G′的拉普拉斯矩阵

式 中：W为 带 权 邻 接 矩 阵，W=(w ij)，i，j=1，2，…，n；D为 带 权 度 矩 阵，D=diag(d i)，d i=

（2）计算标准化拉普拉斯矩阵Lrw的特征值与特征向量

（3）按特征值从小到大取前k个特征向量组成矩阵V=[v1，v2，…，v k]，V∈Rn×k，取V的行向量作为节点的谱空间表征yi∈Rk，i=1，2，…，n，该特征空间中，拓扑邻接且特征描述相似的样本点聚集在一起。

（4）利用谱空间特征向量进行K-means聚类，得到分区结果C′=(c′1，c′2，…，c′k)，其中c′1，c′2，…，c′k为各个分区。

2.2 评价指标

通过MOSC可以得到不同分区数量的分区方案，为了选出在模块度和边界管道数上表现最好的方案，引入综合评价值F，该值是以模块度和边界管道数作为评价指标，通过简单加权归一化公式［17］计算得到，F的计算公式为

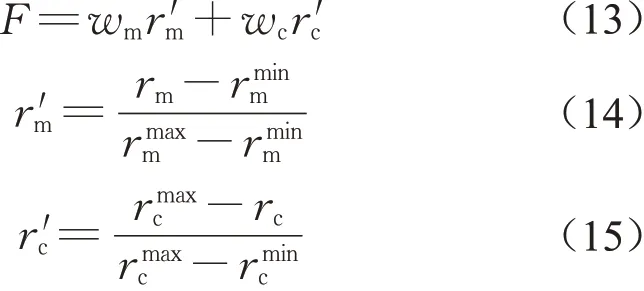
式中：rm、rc分别为分区方案对应的模块度和边界管道数；r′m、r′c分别为归一化后的模块度和边界管道数；wm、wc分别为模块度和边界管道数的权重。

3 案例分析

采用我国某市管径100mm以上的实际供水管网作为实例分析数据，以模块度和边界管道数为指标，分析MOSC与Fast-greedy、SC的对比实验结果，验证MOSC用于供水管网分区的有效性。管网的基本信息如表1。

表1 实例管网基本信息Tab.1 Basic information of water network cases

3.1 对比实验

对实例管网数据利用Fast-greedy、SC和MOSC求解分区，其中Fast-greedy由开源igraph模块实现，SC由sklearn.cluster模块实现。以模块度作为分区形态指标，以边界管道数量作为分区成本指标构建对比实验。以MOSC作为实验组，以Fast-greedy、管径为边权的SC作为对照组进行分区数量10到50的实验，实验结果如图3所示。其中，SC的加权具体计算方式为，将第1.2节中的邻接矩阵A改写为以管径（d）的赋权形式。即

从图3a可以看出，在模块度方面，Fast-greedy与SC差异较大，尤其在分区数较少时，SC模块度迅速降低，整体上也低于Fast-greedy，而MOSC耦合了Fastgreedy，所以保持较高的模块度，最后从MOSC的曲线看出，由于该算法引入了许多分区特征，随着分区数量的减少，MOSC的模块度减少速度明显慢于SC，在分区数较少时也不会损失太多的模块度值；随着分区数量的增多，MOSC的模块度越来越接近Fast-greedy的模块度，直至完全重合，因此通过MOSC所得的分区结果模块度高。图3b可以直观反映出，在边界管道数量上，SC明显低于Fast-greedy，而通过MOSC得到的边界管道数量与SC非常接近。随着分区数量的增多，尤其是分区数量在16及以上时，MOSC与SC的边界管道数曲线完全重合，因此MOSC所得的边界管道少。MOSC耦合了Fast-greedy和SC，使得该算法集成了这2种算法的优点，在保持较高模块度的条件下，能尽量减少边界管道的数量，该算法在模块度和边界管道数上表现比较均衡。

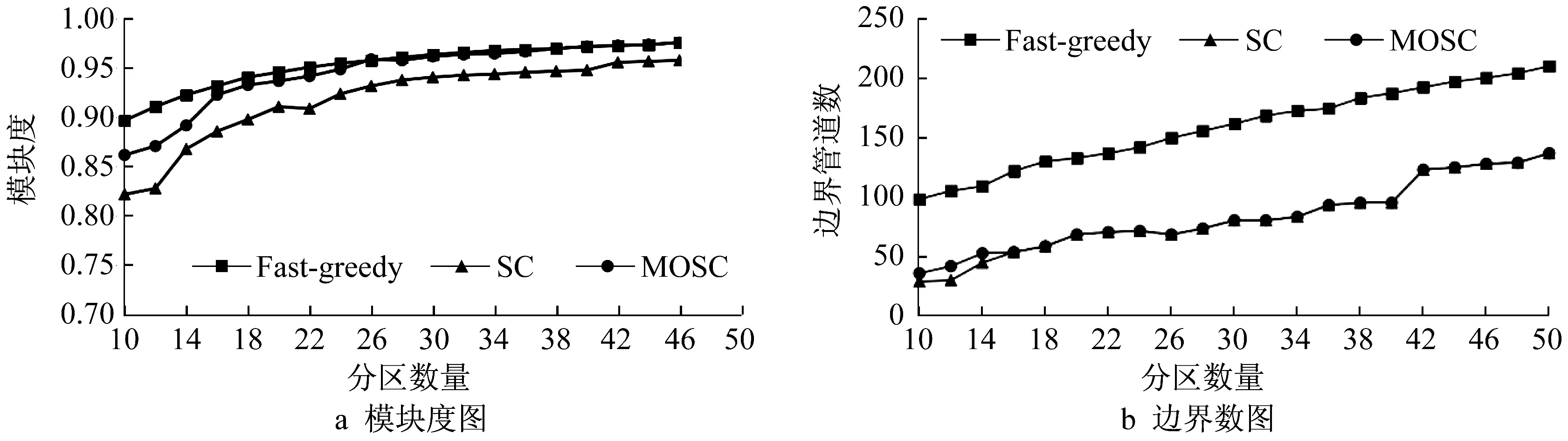
图3 对比实验结果Fig.3 Comparison of experimental result

3.2 MOSC有效性

图4显示了利用MOSC得到11～35个不同分区数量方案对应的模块度和边界管道数。以模块度和边界管道数作为综合评价指标F的重要依据，其权值为wm=wc=0.5。得到从11～35这25个不同分区方案的综合评价值，如图5所示。

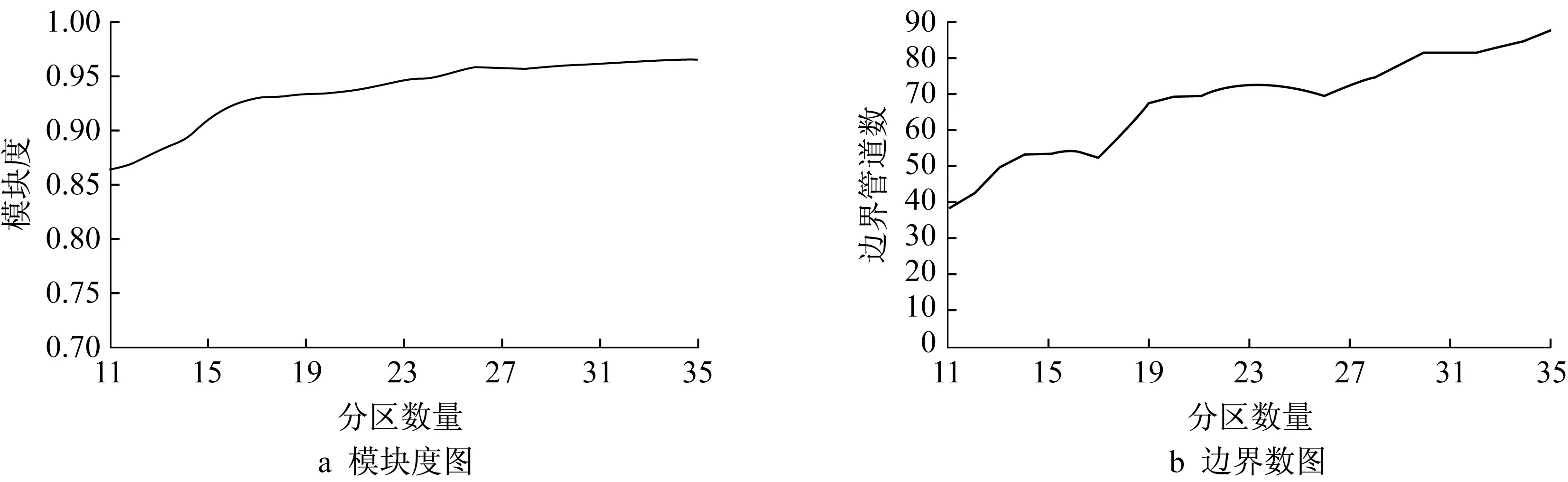
图4 MOSC实验结果Fig.4 MOSC of experimental result

图5 分区方案综合评价Fig.5 Overall merit of partition plan

分析图5发现，分区数量17的分区方案综合评价值F（0.653）最高，所以采用分区数量17的分区方案。分别利用Fast-greedy、以管径为边权的SC和MOSC对该实例供水管网进行分区数量17的分区实验，对应的模块度和边界管道数量如表2所示。在MOSC进行分区的过程中，通过Fast-greedy对该实例供水管网图G进行社区划分，得到数量为360、模块度为0.998的社区划分结果，并构建社区划分对偶图，结合平均管径、平均管长、平均节点高程的水力特性以及各类POIs数量的功能结构特征计算相似性矩阵，实现SC，得到该方案的分区结果。3种算法所得的分区结果如图6所示。

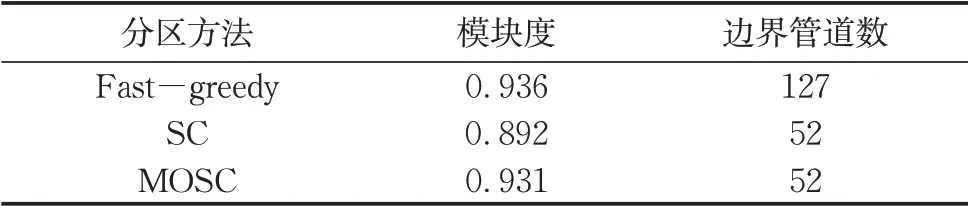
表2 分区数量17的对比结果Tab.2 Comparison of Section No.17

分析图6d发现，MOSC捕获到了管网的单中心空间布局，将管网密度较大的中心城区管网划分为1、2、3这3个分区，市郊划分为其他分区；分析图6b、6c、6d发现，对比这3种算法所得的分区边界形状，Fast-greedy和SC的结果都产生了狭长型无效分区，图6b和图6c中标注的数字1到6分别代表6个不同分区，对比图7a、7b、7c，图7a的1分区中，有两部分已经延伸到了2分区中，这两部分即为狭长型无效分区，从空间位置上来说，它们本该属于2分区，这是由于Fast-greedy仅仅只考虑了管网中管段间的拓扑结构，只是依次合并相邻的2个社区，并没有考虑管段的空间位置，同样图7b的1分区中，也出现了狭长型无效分区，加权SC只是以管径作为边权重，构建相似度矩阵，同样也是依赖管段间的拓扑结构，而在MOSC社区划分对偶图构建过程中，以管段管长、节点高程等为水力特征，尤其是以该市各类POIs数量作为管网空间区位特征，综合这2种特征所得到的对偶图边权重，考虑了管段空间位置，将空间上更邻近的管段划分在同一分区，如图7c所示，相对于这2种算法MOSC不会产生该类型的分区。

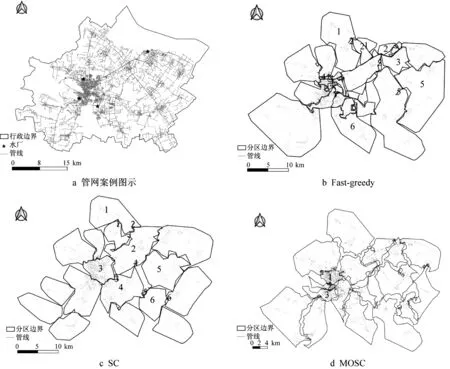
图6 3种算法分区结果Fig.6 Partitioning result of three algorithms

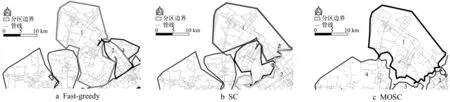
图7 3种算法分区局部结果Fig.7 Partitioning local results of three algorithms

4 结论

利用Fast-greedy对管网的高模块度社区划分能力以及SC对于最小边界管道的识别能力，提出一种耦合模块度优化与谱聚类的管网分区算法MOSC。对比该算法与Fast-greedy和SC在模块度以及边界管段数量的表现，证明MOSC克服了Fast-greedy在处理分区边界较弱以及SC在模块度方面表现较差的缺点。MOSC算法相较于Fast-greedy算法和SC算法，所得分区方案具有模块度高、边界管道数量少的特点，而漏损控制则需要对区域内所有边界管道上的阀门、流量计进行清晰划分。因此，MOSC算法所得DMA分区不仅界限分明，没有出现狭长型无效分区和空间位置上的交叉重叠从而有利于水司进行分区的日常管理和维护，而且较少的边界管道有利于在漏损控制过程中减少阀门、流量计等设备的数量从而节省分区成本。本文提出的MOSC进行管网分区，考虑管径、管长、材质、管段数量等水力拓扑特征，后续可以引入更多诸如节点压力、水龄、用户数等特征，以进一步优化分区结果。

作者贡献声明：

杨之江：提出研究选题；设计研究方案；论文撰写、修订。

周煜岷：调研整理文献；实施研究过程；论文撰写。

扈 震：技术支持；指导性支持；终审论文。

曾 文：指导性支持；技术支持。

周 扬：实验验证。

李晓丽：数据获取及加工。

冯 丽：实验验证。