基于改进区间逆响应面法的塔机有限元模型修正

秦仙蓉，龙世让，丁 旭，张晓辉，孙远韬，张 氢

（同济大学机械与能源工程学院，上海 201804）

塔式起重机（简称塔机）是国家现代化发展和城镇基础设施建设中非常重要的机械设备。作为各类高层建筑和大型建设工程必不可少的施工设备，从1950年到2018年为止，国家塔机拥有总量从几十台飞速发展到234.79万台，各种塔机年产量接近1万台，生产规格多达18种，起重量最大突破400t，极大促进了国家的发展［1］；但是，在使用过程中塔机也造成了很大的安全事故，据统计，在2012至2018年间塔机事故发生总数为565起，死亡人数达799人，占建筑、机械等行业事故总量的6%～20%［2］。考虑到塔机发生破坏对施工人员所产生的影响，从而对其安全性也提出了更高要求。但由于在役塔机因为受到载荷作用、施工安装差异、环境侵蚀等因素的影响，其结构性能也与初始设计不完全一致，两者的共同作用使得根据塔机有限元模型预测的结构特性与实测结果之间不可避免地出现模型参数误差，降低有限元分析结果的可信度，从而必须以实测响应为基础对其进行修正优化，获取与实测结构相符的有限元模型，方可为塔机的健康分析提供参考［3］。因此必须对塔机进行有限元模型修正，得到准确的结构参数，才能进一步由更新的结构参数得到精准描述其静动力学特性的有限元模型，据此进行进一步的分析与监测塔机力学特性，确保塔机工作在安全状态。

目前，有限元模型修正主要有2类：矩阵型修正法和设计参数型修正法。在各种有限元模型修正方法中，响应面方法［4］通过建立特征量与设计参数间的响应面模型，避免了每次迭代时的有限元重分析，降低了计算量，因此，秦仙蓉等［5-7］将响应面法应用于有限元的模型修正之中。但响应面法仍需进行多次迭代，修正效率较低。为此，张伟杰等［8］受逆系统方法启发提出了逆响应面法，通过对调传统响应面模型的自变量和因变量，直接将实测响应数据代入响应面模型获取最优值，省略迭代优化步骤，极大提高修正效率，张挣鑫等［9］将其应用于桥梁的模型修正中，验证了这一方法的可行性。但是，逆响应面模型仅适用于确定性模型修正，为了解决含不确定性参数的问题，骆勇鹏等［10］引入了模态区间分析方法，扩大了逆响应面法的适用范围。但是，区间逆响应面法同样存在3个缺陷：首先，区间逆响应面模型基于二次多项式构造，适用于简单结构，若研究对象较复杂（如本文塔机），则建立的区间逆响应面模型无法根据频率预测参数的真实值；其次，在响应面模型构造时，由于不确定性问题的复杂性，参数的真实区间很可能在参数抽样空间之外，根据工程经验初定的参数值得到的区间逆响应面模型就无法预测出参数的真实区间；最后，在区间逆响应面模型构造过程中，还需对所建立的模型进行强制最优理论变换，操作繁琐。

基于此，本文提出改进区间逆响应面模型修正方法，保证对复杂结构仍能够进行高精度、高效率的有限元模型修正，以得到更为精确的有限元模型，并以塔机作为实际算例验证本文提出方法的有效性。

1 改进区间逆响应面法

基于二次多项式的传统逆响应面数学模型如式（1）：

式中：xk为第k个输出变量（本文为待修正设计参数）；s为输出变量的个数；yi为第i个输入的结构特性（本文为模态频率）；r为模态阶数；ξ0、ξi、ξii、ξij为函数的各个待定系数。

但上述模型仅适用于简单模型，对于复杂结构而言，为了使所建立的区间逆响应面模型精度更高，常采用更多抽样次数，保证参数样本在约束区间内分布更为均匀。但也因此导致样本数量过大，为解决这一问题，本文采用RBF神经网络代替二次多项式作为区间逆响应模型的拟合函数。其独特优势在于结合了神经网络和RBF核函数的优点，可以使用大样本数据对模型进行训练，同时还具有很强的非线性拟合能力，可映射任意复杂的非线性关系，这是二次多项式所不具备的。RBF神经网络的逆响应面表达见式（2）：

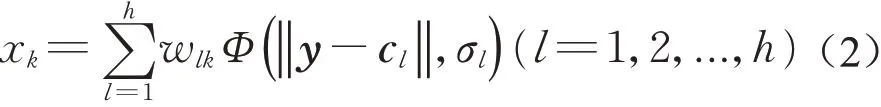
式中：y为结构频率输入；c l、σl分别为第l个神经元的中心和宽度；h为隐含层神经元的个数；Φ（||y-c l||，σl）为径向基函数；w lk为第l个隐含层节点到第k个输出节点的连接权值。

针对区间逆响应模型的样本点可能在真实区间之外的情况，本文在构造区间逆响应面模型前，先依据频率空间中心对塔机进行一次确定性模型修正工作，并根据所得到的修正参数值进行试验设计建立区间逆响应面模型，确定性模型修正的目标函数如式（3）所示：

式中：为有限元模型第m阶固有频率；为实测频率空间中心的第m阶频率；、x_分别为设计变量变化范围的上、下限。

本文模型修正主要分2步进行：①根据实测频率空间中点构造目标函数，对塔机参数进行确定性模型修正，得到修正后的参数值；②根据修正后的参数值在参数约束区间内抽样构造区间逆响应模型，代入实测数据，得到参数的预测值和预测区间，并判断预测区间是否在抽样区间之内。其具体修正流程如图1所示。

图1 基于改进区间逆响应面法的塔机不确定性模型修正流程Fig.1 Flowchart of finite element model updating of tower crane with uncertain parameters based on improved interval inverse response surface method

由于区间逆响应面模型的输出为设计参数，故其精度检验方法与传统的响应面模型有很大差别，本文采用平均相对误差对其预测精度进行检验，如式（4）所示：

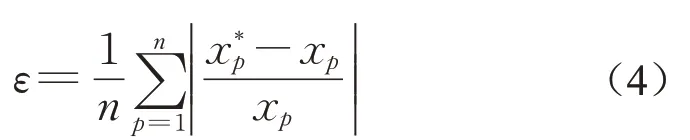
式中：n为试验中设计变量的分组数（样本数）；x p*为区间逆响应面模型预测值；xp为区间逆响应面试验设计参数。

2 方法验证：三自由度弹簧-质量系统

选用三自由度弹簧-质量系统［11］对所提出的区间修正方法进行验证。图2所示是一个三自由度弹簧-质量系统，为了验证本文所提出的区间修正方法在复杂情况下的修正效果，本算例讨论的不确定性参数为刚度系数和质量系数。

图2 三自由度弹簧-质量系统Fig.2 Three degree of freedom spring mass system

系统中各确定性参数取值参考如下：

弹簧-质量系统修正优化的目标函数、不确定性参数及其取值区间为

以此来模拟刚度系数和质量系数联合修正的情形。在参数区间范围内使用拉丁超立方抽样方法构造30组样本，作为数值算例的“实测”结果，并基于响应空间中心构建目标函数对初始有限元模型进行第一次确定性模型修正，目标函数和刚度质量系数的收敛曲线分别如图3所示。可以看出，在前4次迭代时，目标函数的下降速度较快，此时各系数变化较为明显，经过大约13次迭代后，3个系数变化趋于稳定，问题近于收敛。

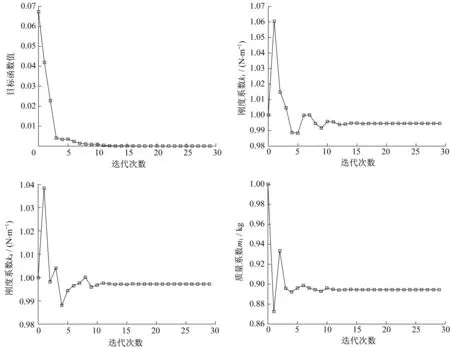
图3 弹簧-质量系统目标函数及各系数收敛曲线Fig.3 Objective function of spring mass system and convergence curve of each coefficient

将参数的修正值作为区间逆响应面模型的抽样空间中心，在上下摄动50%范围内进行抽样，抽取100组样本构建区间逆响应面模型，之后采用该样本数据和重抽样的20组数据对该区间逆响应面模型的预测精度进行检验，从表1的结果可看出所构造的区间逆响应面模型的参数预测精度较高。

表1 弹簧-质量系统区间逆响应面模型精度检验Tab.1 Accuracy test of interval inverse response surface model for spring mass system

基于构建的区间逆响应面模型和系统“实测”频率数据对参数进行预测，得到修正区间如表2所示。可知当联合质量和刚度参数修正后，仅有k4的上下界存在较小的误差，其余参数的上下界误差均接近零，这说明针对联合修正问题，本文所提出的修正策略是可行的，并且区间修正精度较高。

表2 三自由度弹簧-质量系统修正前后变量区间误差对比Tab.2 Comparison of variable interval errors before and after updating of 3-DoF spring mass system

将参数修正前后的频率空间进行对比，结果如图4所示。可知：修正后频率空间与真实频率空间较为贴合，且实测数据点基本都落在修正空间内部，也落在初始空间内部，这说明基于区间逆响应面法进行不确定性有限元模型修正是可行的；同时还可看出，在进行刚度和质量参数联合修正时，响应空间的非线性特征较强。

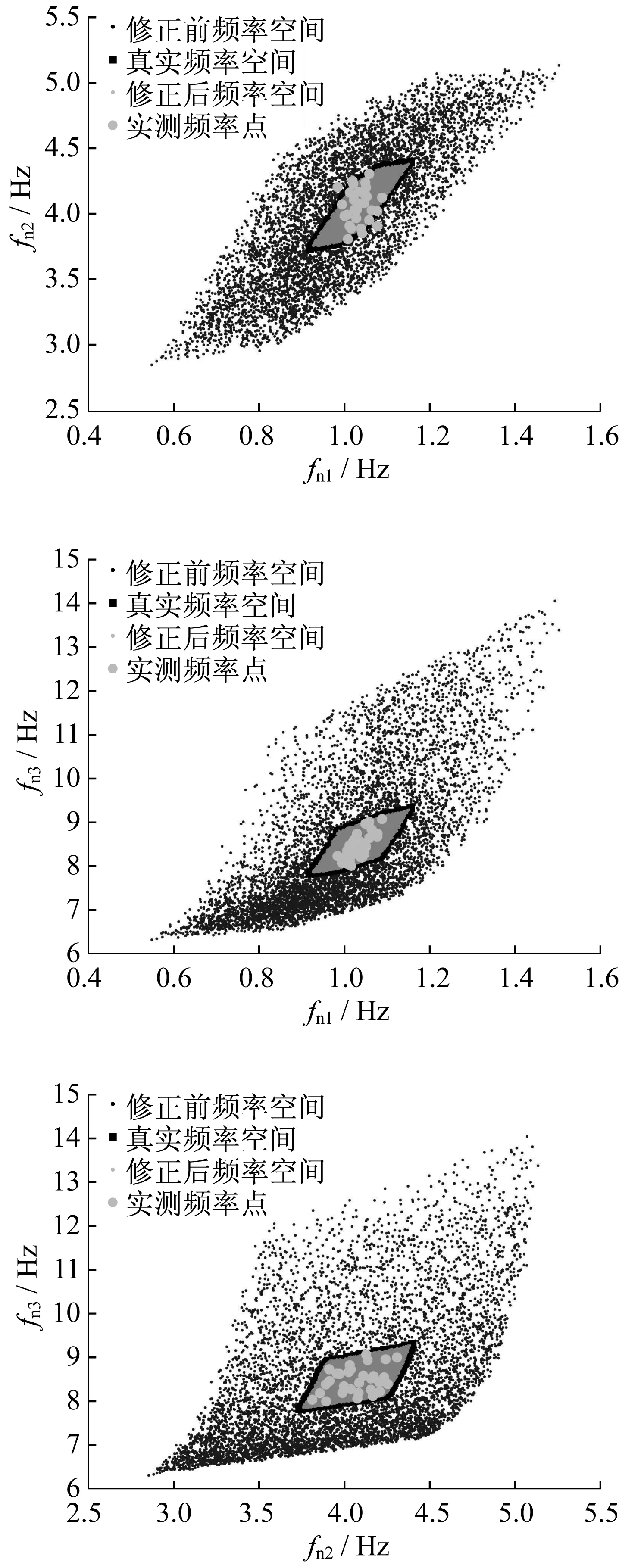
图4 弹簧-质量系统修正前后频率空间对比Fig.4 Frequency space comparison of spring mass system before and after updating

3 某型实际塔机的不确定性有限元模型修正

数值算例的修正结果表明基于区间逆响应面法对含不确定性参数的有限元模型进行修正是可行的，且该方法结合了响应面模型，相比迭代优化方法具有更高的计算精度和效率，因此能够应用在复杂机械结构塔机的模型修正中。

某型塔机结构如图5所示。根据其设计图纸建的对应有限元模型，其中塔身、塔基、起重臂、平衡臂及塔帽等结构采用考虑剪切效应的三维梁单元Beam188，起重臂和平衡臂的拉杆采用杆单元LINK10，塔机的工作机构、电气设备、梯子栏杆、配重等附属构件以集中质量单元MASS21建立在相应位置，根据塔机实际情况，将标准节与标准节之间、加强节与加强节之间采用固结处理，起重臂各节臂之间、拉杆与塔顶之间、两臂与回转塔身之间采用铰接连接，塔基边界条件设置见文献［6］。最终整个模型包含5 502个单元，11 052个节点，共66 320个自由度。

图5 某型塔机及其主要部件Fig.5 Components of a tower crane

对塔机进行模态分析后，其前5阶模态分别为：起重臂在回转平面内的一阶弯曲、起重臂在起升平面内的一阶弯曲、塔身在回转平面内的一阶弯曲、塔身在起升平面内的一阶弯曲以及起重臂在回转平面内的二阶弯曲。

结合塔机前5阶模态以及Sobol全局灵敏度分析，选择表3所示6个设计参数作为某型实际塔机不确定性修正变量，其目标函数为

在塔机区间逆响应面模型构造时，不确定性参数的抽样范围和样本点数量均需根据实测频率数据不断进行调整，以确保修正后参数区间在抽样范围内，最终得到的修正变量的抽样区间如表3所示。表中x1为塔身标准节主肢长度，x2为上塔身水平腹杆长度，x3为塔身水平腹杆长度，x4为塔身主肢截面宽度，x5为塔身主肢截面厚度，x6为弹性模量。

表3 塔机结构的不确定性修正变量和抽样区间Tab.3 Uncertainty correction variable and sampling interval of tower crane structure

为保证所建立的区间逆响应模型的精度，在修正变量的抽样区间内采用拉丁超立方抽样法抽取400组数据构造区间逆响应面模型，分别使用原始样本点和20组重抽样样本点对逆响应面模型进行精度校验，其精度较高，参数的平均预测误差较小。将塔机振动实测数据代入到区间逆响应面模型中进行参数预测，得到的参数区间修正结果如表4所示，可看出：经过改进区间逆响应面法修正后，各参数的区间范围均有明显的缩小，且修正后的参数区间均在初始区间范围内，这也说明修正结果是合理的。

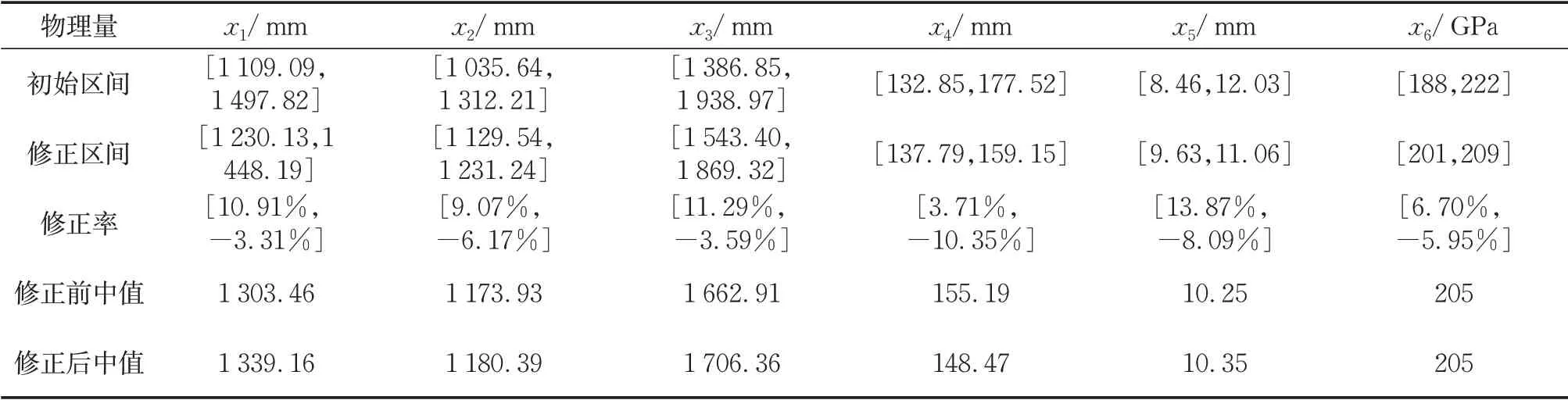
表4 塔机修正后不确定性参数的区间范围Tab.4 Interval range of tower crane uncertainty parameters after updating

同前述算例一样对塔机修正前后频率空间进行对比，得到塔机模态频率空间的投影云图，各阶次如图6所示。分析可知：在频率空间内，各阶频率响应并不呈均匀分布，这是由于塔机结构过于复杂导致。通过本文的方法修正后，频率修正区间相较频率初始空间有了明显的减小，且实测数据点均落在频率修正区间内，这说明该方法可有效对塔机结构进行不确定性修正。同时也可看出实测数据点的分布过于集中而非均匀分布在预测区间内，这是由于塔机实测频率的不确定性程度较小导致。

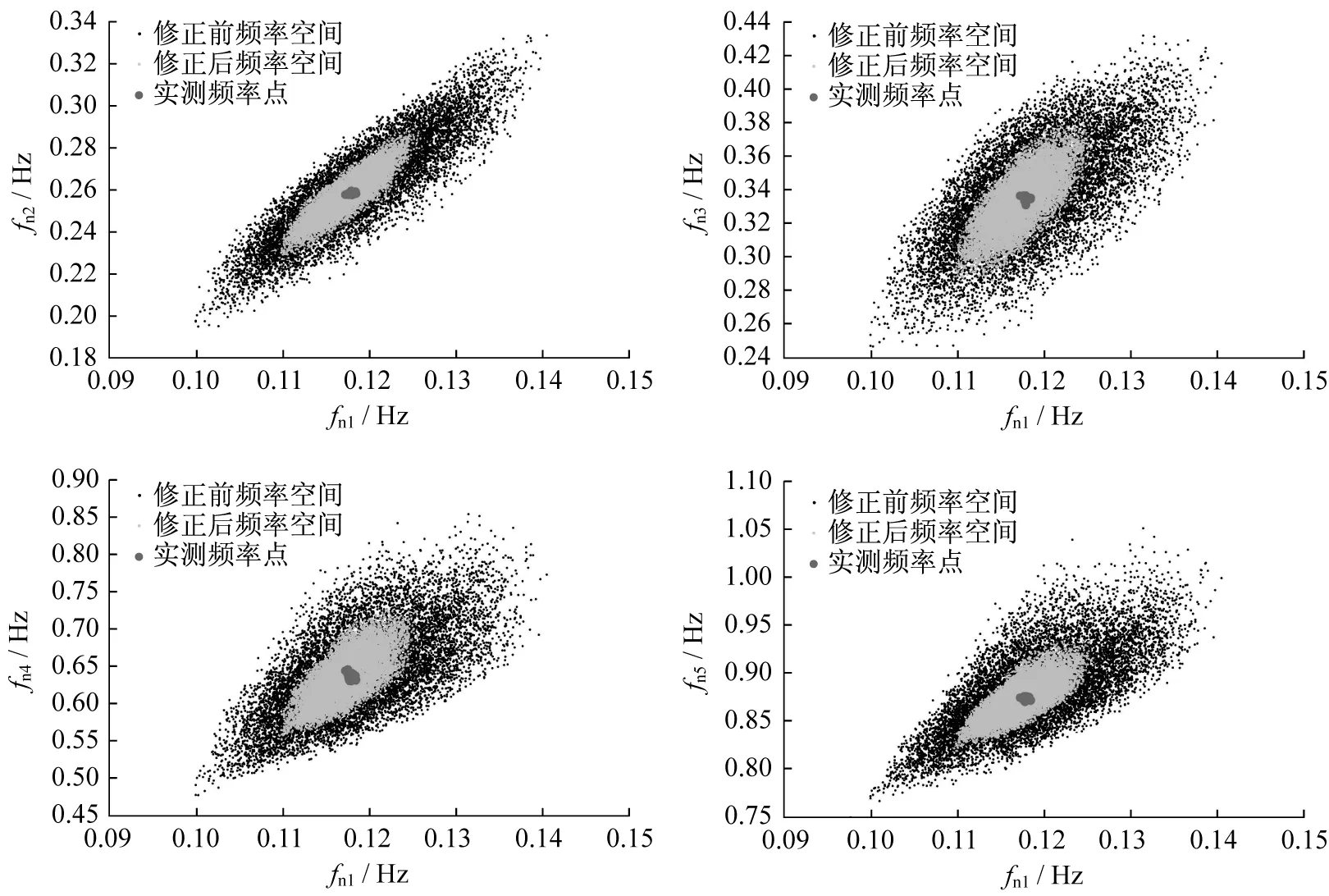
图6 塔机修正前后频率空间对比Fig.6 Frequency space comparison of tower crane before and after updating

4 结语

提出了一种基于改进区间逆响应面法的有限元模型修正方法，采用RBF神经网络作为区间逆响应模型的拟合函数，并以数值算例对该方法的可行性进行了验证，最后结合塔机实测数据获得了更好的修正结果，得到的结论如下：

（1）区间逆响应面法可有效解决由于参数不确定性而引起频率不确定性的问题，从算例及塔机修正结果可知区间参数的修正精度较高，并且该方法应用简便。

（2）RBF神经网络响应面模型构造简单、适用性较强，非常适合大样本数和多特征问题，且其在构造区间逆响应面模型中具有很高的精度，相比于多项式响应面模型更加适合本文对象塔机的研究。从塔机的实际修正结果来看，其修正结果也更加精确。

作者贡献声明：

秦仙蓉：项目的构思者及负责人，指导项目思路、数据分析、论文写作与修改。

龙世让：模型建立和仿真研究的执行人，完成数据分析、论文初稿的写作。

丁 旭：参与建模和试验结果分析。

张晓辉：参与建模和试验结果分析。

孙远韬：指导项目思路、论文写作与修改。

张 氢：指导项目思路、论文写作与修改。