无人机GNSS-R时延多普勒计算关键技术
刘原华,刘张文,牛新亮
无人机GNSS-R时延多普勒计算关键技术
刘原华1,刘张文1,牛新亮2
(1. 西安邮电大学 通信与信息工程学院(人工智能学院),西安 710121;2. 中国空间技术研究院西安分院,西安 710000)
针对海面风场反演中,采用不同的镜面反射点估计算法计算结果存在较大差异,导致等延迟环和等多普勒带的大小和分布不同,从而使得散射信号二维时延-多普勒相关功率计算的不一致等问题,提出在机载场景下,利用接收机相对于卫星发射机的仰角,来计算二维相关值参考点的时延和多普勒的方法。实验结果与实测数据对比表明,机载条件下,采用该方法计算真实有效,且无需计算镜面反射点的位置,简化了计算过程。
镜面反射点;时延;多普勒;卫星高度角;全球卫星导航系统反射信号
0 引言
在全球卫星导航系统(global navigation satellite system, GNSS)众多应用领域中,GNSS反射信号(global navigation satellite system-reflection, GNSS-R)处理技术是20世纪90年代发展起来的。GNSS-R技术的基本原理是利用反射面反射的导航卫星的伪随机测距码信号或者载波信号,反演目标物体表面性质。与传统的卫星散射计和雷达高度计等采用后向散射单基工作模式相比,GNSS-R技术工作模式为收发分离的双(多)基雷达模式。其特点和优势为不需发射机、有大量信号源、采用扩频通信技术和应用面宽4个方面[1]。现已被广泛应用于海面风场反演[2-3]、海洋盐度探测[4]、土壤湿度探测[5-6]等。由此可见,GNSS-R技术具有重要的研究价值和广泛的应用前景。
在GNSS-R反射信号应用中,为了获取有效的反射信号二维相关值,需要正确选取二维相关值的时延-多普勒参考点,一般采用镜面反射点处的时延值和多普勒值作为参考点[1]。现有的镜面反射点估计算法有文献[7]提出的格里森(Gleason)算法、文献[8]提出的S.C.WU方法、文献[9]提出的C.万格(C.WANGNER)算法、线段二分法[10]、黄金分割法[11]等。首先,文献[9]中算法假设地球为标准圆,而实际上地球是椭球的,因此估计偏差较大。文献[7]中的Gleason算法、线段二分法、黄金分割法等算法是基于地球基准椭球面来计算的,但是在迭代过程中忽略了地形海拔高度的影响。其次,以上传统方法是以镜面反射点处入射角等于反射角作为迭代终止的条件,而由于地球是椭球面,GNSS-R几何关系中的入射角和反射角与斯涅耳反射定律中入射角和反射角的定义不同,也导致镜面反射点计算存在误差,从而参考点的时延多普勒值计算存在误差,进而导致反射信号二维相关值功率计算出现偏差。
一般来说,星载条件下,观测到以镜面反射点为参考点的16个码片延迟即可满足反演要求;而机载条件下,应用场景为6个码片范围[1,12]。星载平台下,由于接收机高度足够高,等延迟环分布广,由传统方法产生的误差可以忽略不计;而机载平台由于接收机高度限制,计算出来的镜面反射点有可能已经超出了接收机的波束范围,而且6个码片延迟以外的区域因为远离镜面反射点,散射功率较弱,且存在较大噪声,不可用来反演风速,因此机载平台下以上误差不能够忽略。本文通过研究GNSS-R基本几何关系和传统的镜面反射点估计算法,针对机载条件下提出了一种散射信号二维相关值参考点时延多普勒计算方法。
1 GNSS-R基本几何关系
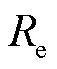
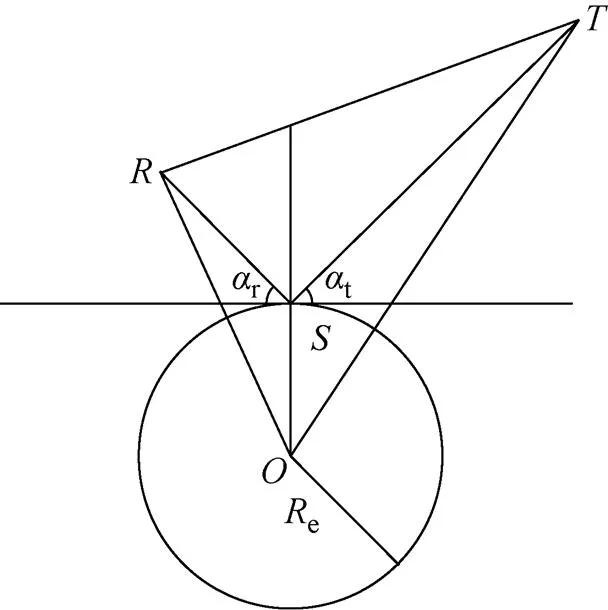
图1 GNSS-R基本几何关系
2 不同算法比较及误差分析
2.1 4种算法引用结果对比
为了验证前文提出的镜面反射点计算存在误差,通过引用已有文献中不同算法(Gleason算法、S.C.WU算法、最短路径法和线段二分法)[10,13]在同一组卫星发射机和接收机位置数据下的计算结果,进行误差分析。这些算法使用的都是来自英国灾害监测星座(United Kingdom-disaster monitoring consortium,UK-DMC)卫星在2004-11-16测得的一组海洋数据,通过比较这些不同算法计算出的镜面反射点在地球表面的偏差量,来阐明传统方法计算镜面反射点存在着固有的误差,即求不出一个镜面反射点的真值。
本文发射机数据采用全球定位系统(global positioning system,GPS)22号卫星位置数据,位置为(-11178791.99129,-13160191.20499, 20341528.12754),单位为m;接收机位置为(-4069896.70338, -3583236.96373, 4527639.27175),单位为m;地球半径均采用1984世界大地坐标系(world geodetic system 1984,WGS-84)地球椭圆模型计算。不同算法计算结果见表1。

表1 不同算法镜面反射点计算结果 单位:m
如表1所示,不同的算法计算结果在地球表面的位置坐标不同,存在着不一致性,镜面反射点存在着几十千米级别的偏差。
2.2 镜面反射点处时延值的计算
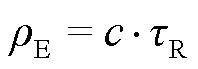

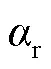
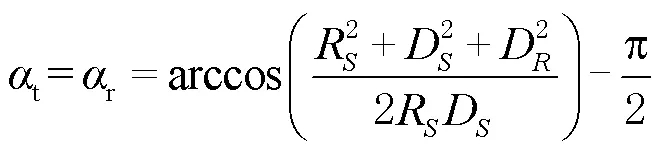
2.3 镜面反射点处多普勒值的计算
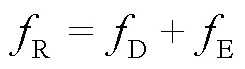
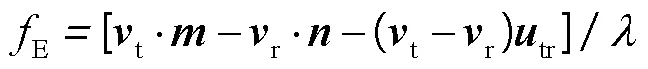
同理,镜面反射点处多普勒频率的计算也与入射角、反射角有关,机载条件下同样不能忽略镜面反射点计算的偏差。
2.4 等延迟环的大小和分布
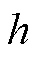
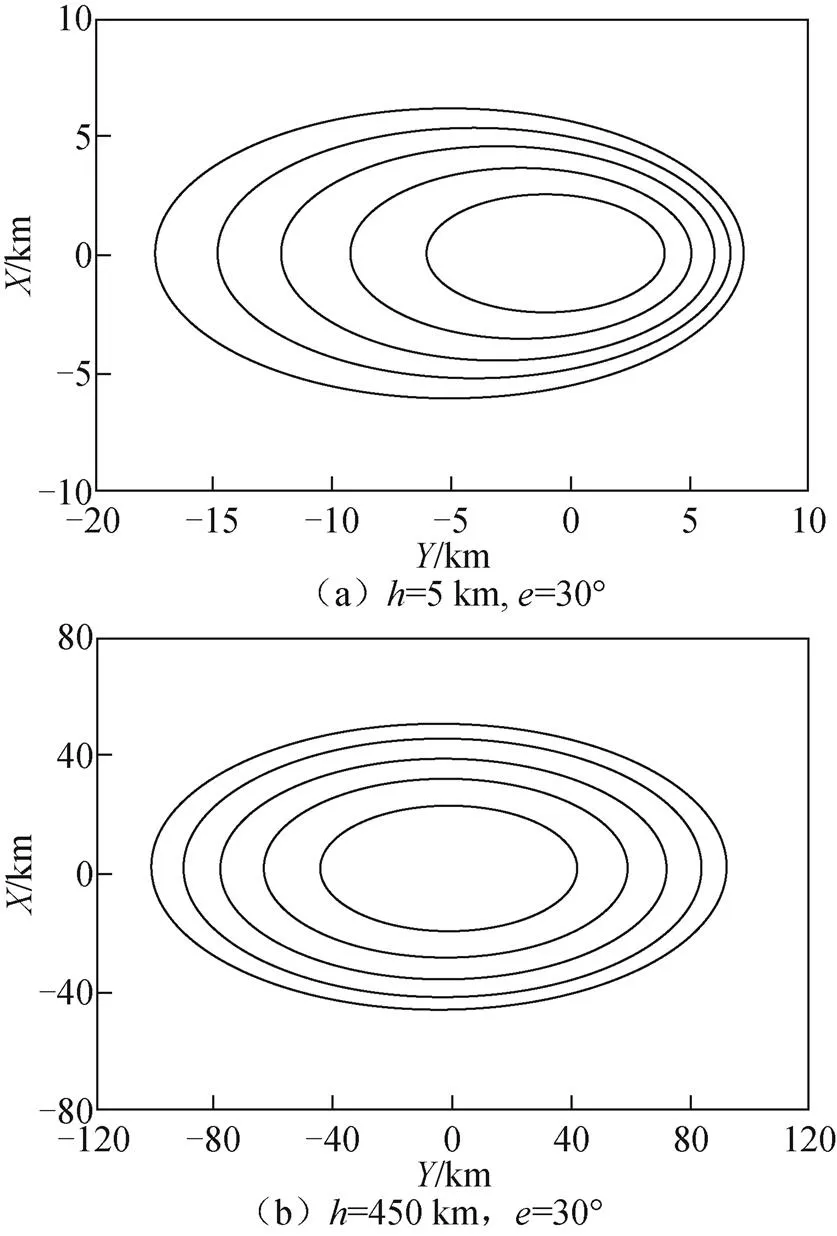
图2 不同场景等延迟环大小和分布
由图2可以得出:星载平台的等延迟环远大于机载平台,表明接收机高度越高,等延迟环面积越大,对应的散射信号的能量区域也越大。机载条件下,一般观测到6个码片延迟即可;接收机高度为5 km时,第1~第5等延迟环的大小在-20~10 km范围内,再结合表1数据可得,传统方法计算的镜面反射点存在着千米级别的偏差,会影响等延迟环的分布,且有可能偏出等延迟环的范围。
综上分析,为了提高机载平台反演精度,需要重新计算二维相关值参考点的时延多普勒。
3 无人机时延多普勒计算方法
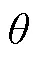
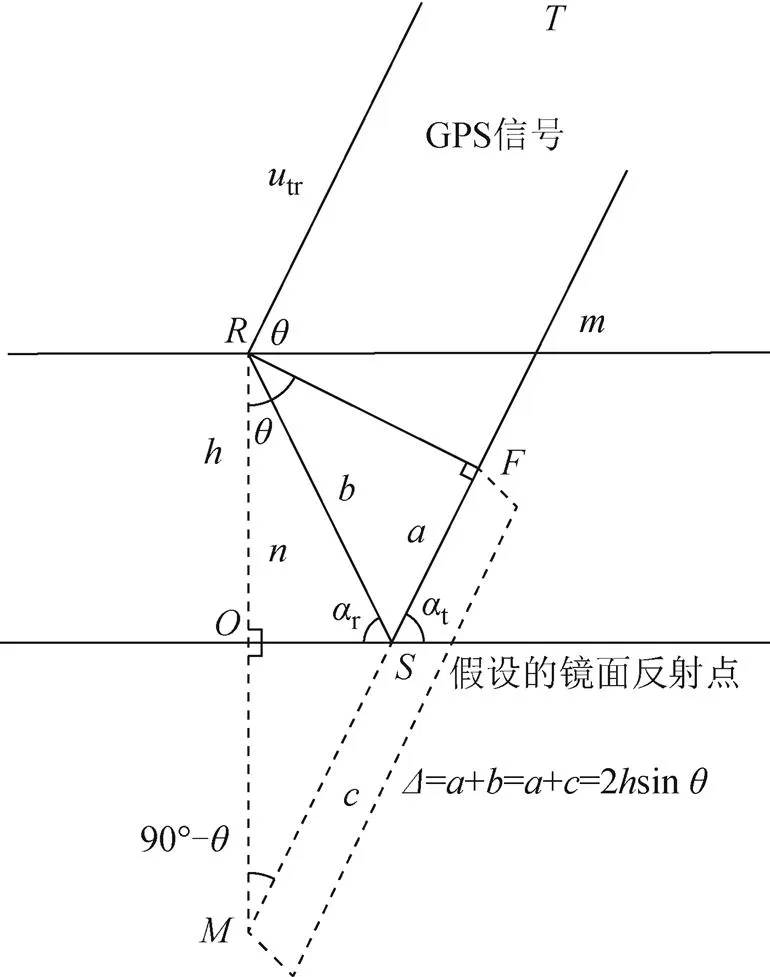
图3 机载场景下时延多普勒计算模型
3.1 机载场景时延计算方法
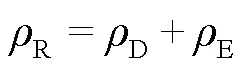
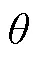

3.2 机载场景多普勒频移计算方法
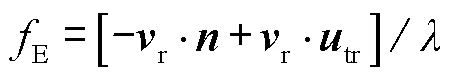
4 试验验证与分析
为了验证前面提出的机载条件下时延和多普勒计算方法的准确性,本文通过无人机飞行实验以及矩阵实验室(matrix laboratory, MATLAB)仿真软件进行作图分析。通过本文方法计算无人机飞行时延和飞行多普勒值,并与实测信号的信号时延和信号多普勒值进行对比,验证计算的参考点时延和多普勒频移的准确可用性。
实验中无人机的飞行轨迹如图4所示。

图4 无人机实验飞行轨迹
无人机飞行高度为4000 m,飞行速度为50 m/s。根据式(7)和式(8)计算参考点反射信号相对于直射信号的时延和多普勒值。计算出的飞行时延值和飞行多普勒值如图5、图6所示,计算出的飞行时延为25 μs,飞行多普勒为100 Hz。
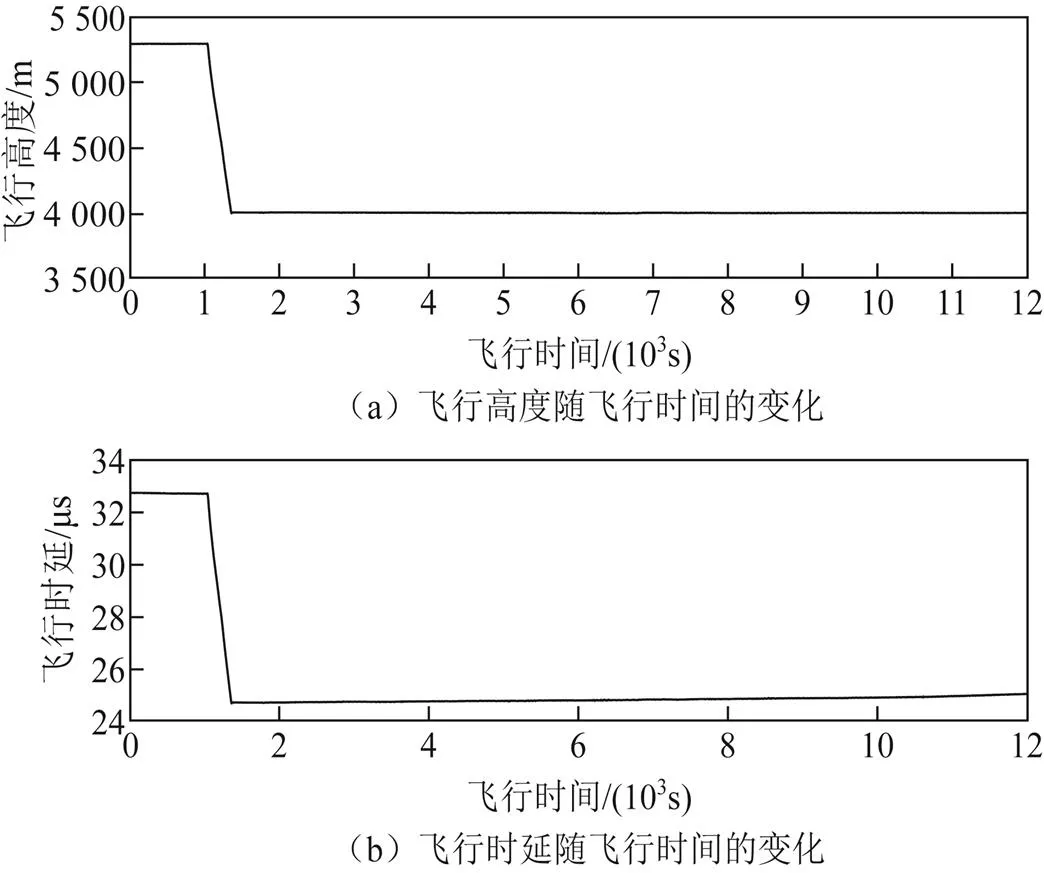
图5 无人机飞行高度和飞行时延
与实测信号的信号时延和信号多普勒值进行对比,如图7、图8所示。
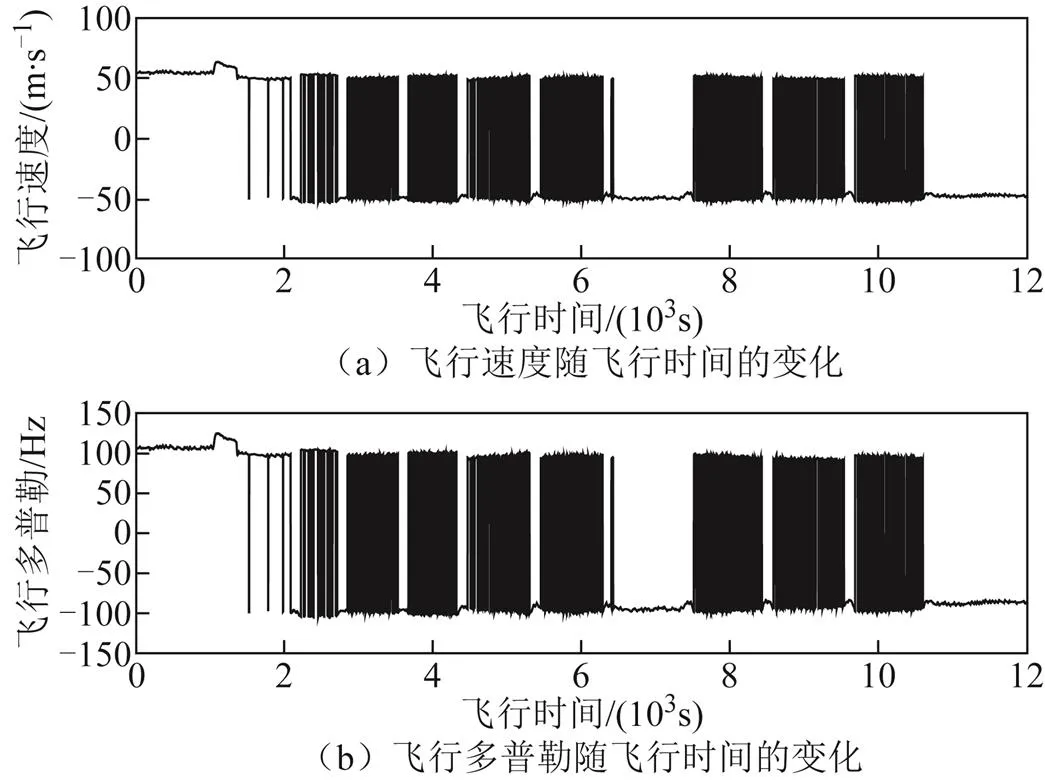
图6 无人机飞行速度和飞行多普勒

图7 无人机飞行时延与信号时延
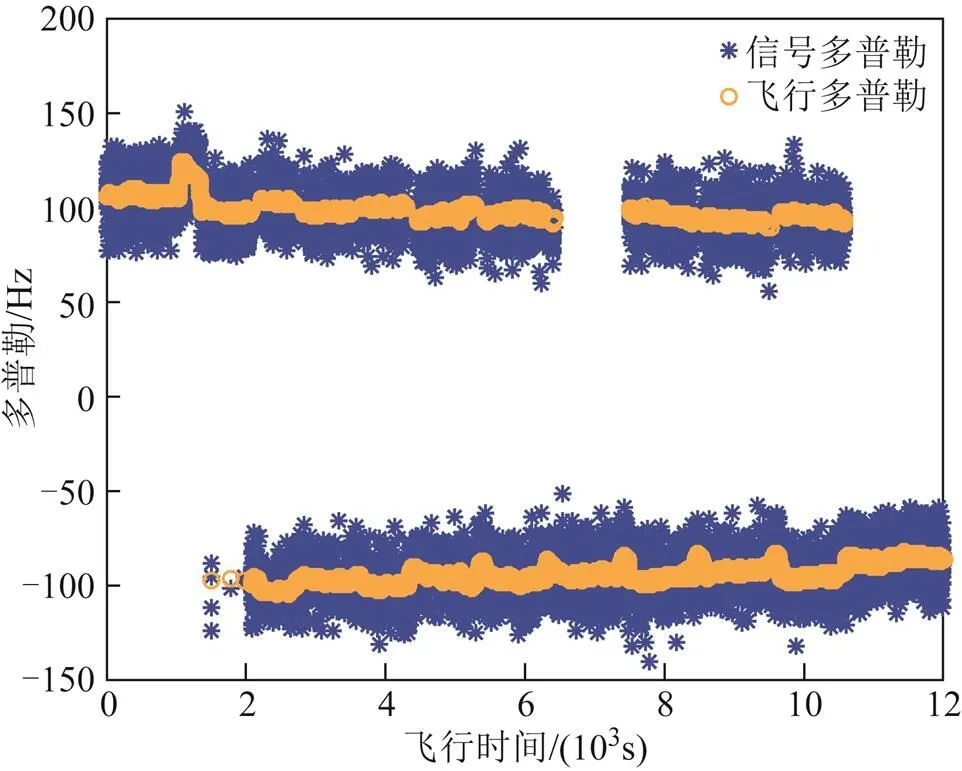
图8 无人机飞行多普勒与信号多普勒
根据图5和图7,无人机飞行高度、飞行时延值和实测信号时延值呈现着相同的曲线分布,随着飞行高度由5292 m下降到4000 m,飞行时延和实测信号时延值均呈下降趋势,这正与式(7)时延计算与无人机高度呈正相关相匹配。在飞行高度为5292 m左右时,实测信号的时延值在32.6~32.8μs;在飞行高度稳定在4000 m时,实测信号的时延值在24.9~25.2μs。而飞行时延均值约为信号时延值的中间值。根据图4、图6和图8可知,无人机在东经112.8°~113.3°之间往返飞行时,飞行速度为50 m/s,飞行多普勒稳定在100 Hz和-100 Hz,实测信号的多普勒值则稳定分布在80~ 120 Hz以及-80~-120 Hz。
为了更直观地对比,计算出的飞行时延与信号时延的偏差、飞行多普勒与信号多普勒的偏差如图9、图10所示。

图9 无人机飞行时延与信号时延偏差
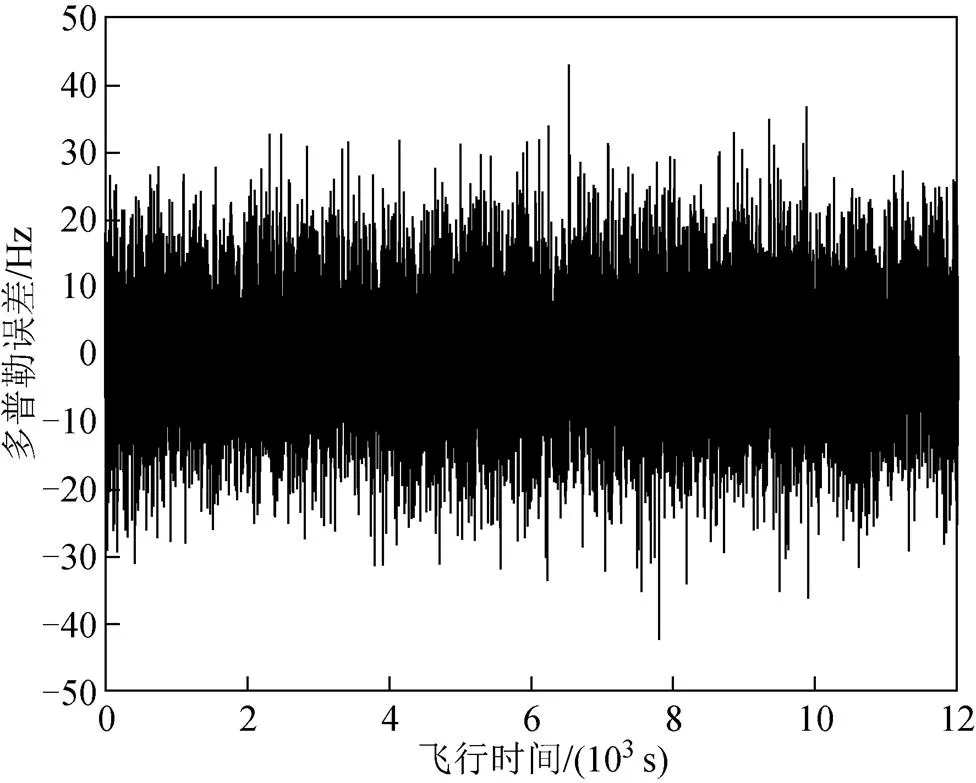
图10 无人机飞行多普勒与信号多普勒偏差
由此可知,本文方法计算出的时延值和实测信号的时延值偏差在0.2μs左右,本文方法计算出的多普勒值与实测信号的多普勒值偏差在20 Hz左右,计算结果误差很小,具有非常高的精度。误差很小的原因如第3节所述,因为无人机飞行高度低,与卫星信号发射机的高度差悬殊,可以认为无人机平台相对于卫星信号发射机的仰角等于卫星信号经地球表面的反射点的入射角。这时计算使用的角度与真实的信号入射角的偏差要小于传统镜面反射点算法计算的角度偏差。由于角度更准确,计算多普勒时无人机的速度投影偏差也更小,时延值的计算也更准确。由此计算出的时延多普勒可用于后续风场反演。
5 结束语
在对GNSS-R的基本几何关系和Gleason算法、S.C.WU方法、线段二分法、最短路径法等镜面反射点估计算法的研究后,得出不同算法之间的计算结果存在着不一致性,存在着千米级别的差距,故本文提出机载平台下的时延和多普勒的计算方法。利用无人机实验和MATLAB作图分析了本文算法,结果表明:本文提出的机载场景下二维时延多普勒图形的参考点时延多普勒计算方法准确性高,且无需计算求解镜面反射点的位置,简化了计算步骤,为后续风场的反演提供了理论依据。
[1] 杨东凯, 张其善. GNSS 反射信号处理基础与实践[M]. 北京: 电子工业出版社, 2012: 7-193.
[2] SCHIAVULLI D, GHAVIDEL A, CAMPS A, et al. GNSS-R wind-dependent polarimetric signature over the ocean[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(12): 2374-2378.
[3] ZAVOROTNY V U, VORONOVICH A G. GNSS-R delay-Doppler maps of ocean surface at weak winds[C]//The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Forth Worth, Texas: IEEE, 2017: 2664-2666.
[4] 王峰,杨东凯. 星载GNSS-R辅助海洋盐度探测方法[J]. 北京航空航天大学学报, 2018, 44(1): 108-116.
[5] RODRIGUEZ-ALVAREZ N, BOSCH-LLUIS X, CAMPS A, et al. Soil moisture retrieval using GNSS-R techniques: experimental results over a bare soil field[J]. IEEE Transactions on Geoscience & Remote Sensing, 2009, 47(11): 3616-3624.
[6] 段睿, 张波, 汉牟田, 等. SVRM方法的单天线GNSS-R土壤湿度反演[J]. 导航定位学报, 2018, 6(1): 34-39.
[7] GLEASON S, GEBRE-GIABHER D. GNSS应用与方法[M]. 杨东凯,樊江滨, 张波, 等译. 北京: 电子工业出版社, 2011: 289-312.
[8] BOEHM J, WERL B, SCHUH H. Troposphere mapping functions for GPS and VLBI from ECMWF operational analysis data[J]. Journal of Geophysical Research (Solid Earth), 2006, 111(B2): 403-408.
[9] WANGER C, KLOKOCNIK J. The value of ocean reflections of GPS signals to enhance satellite altimetry: data distribution and error analysis[J]. Journal of Geodesy, 2003, 77(3/4): 128-138.
[10] 张波, 王峰,杨东凯. 基于线段二分法的GNSS-R镜面反射点估计算法[J]. 全球定位系统, 2013, 38(5): 11-16.
[11] 胡媛, 刘卫. 基于黄金分割法的卫星导航信号镜面反射点预测研究[J]. 高技术通讯, 2016, 26(8): 726-731.
[12] 周旋, 叶小敏, 于暘, 等. 基于GNSS-R的海面风速探测技术研究[J]. 电子与信息学报, 2013, 35(7): 1575-1580.
[13] 刘原华, 贺立庆, 牛新亮. 基于最短路径的GNSS-R镜面反射点算法[J]. 西安邮电大学学报, 2019, 24(6): 16-21.
[14] 万贝, 段崇棣, 牛新亮. 机载GNSS-R海面风场反演信号处理方法研究[J]. 电子设计工程, 2018, 26(7): 63-67.
Key technology of UAV GNSS-R delay and Doppler calculation
LIU Yuanhua1, LIU Zhangwen1, NIU Xinliang2
(1. School of Telecommunication and Information Engineering & School of Artificial Intelligence, Xi’an University of Posts & Telecommunications, Xi’an 710121, China;2. Xi’an Branch of China Academy of Space Technology, Xi’an 710000, China)
There are big differences in the calculation results of different specular point estimation algorithms used in the sea surface wind field inversion, resulting in different sizes and distributions of the equal delay ring and equal Doppler zone, which makes the inconsistency of the scattered signal two-dimensional delay-Doppler correlation power. Aiming at the problems, a method was proposed to calculate the time delay and Doppler of the two-dimensional correlation value reference point by using the elevation angle of the receiver relative to the satellite transmitter in the airborne scene. The experimental results showed that the calculation of this method was true and effective under airborne conditions, and there was no need to calculate the position of the specular point, which simplified calculation process.
specular point; delay; Doppler; satellite elevation;global navigation satellite system-reflection
P228
A
2095-4999(2021)06-0090-06
刘原华,刘张文,牛新亮. 无人机GNSS-R时延多普勒计算关键技术[J]. 导航定位学报, 2021, 9(6): 90-95.(LIU Yuanhua, LIU Zhangwen, NIU Xinliang. Key technology of UAV GNSS-R delay and Doppler calculation[J].Journal of Navigation and Positioning, 2021, 9(6): 90-95.)
10.16547/j.cnki.10-1096.20210614.
2021-02-23
陕西省自然科学基础研究计划项目(2016JQ6033)。
刘原华(1983—),女,陕西西安人,博士,副教授,研究方向为卫星通信、导航和遥感。
刘张文(1995—),男,安徽安庆人,硕士研究生,研究方向为卫星通信、海面风场反演。

