浅谈几何画板在中学教学中的应用
蔡佳兴

摘要:现代信息技术的发展促进了教学手段的革新,几何画板作为现代信息技术教学软件的代表之一,其以动态直观、操作简明的优点受到广大教师的喜爱和推崇。本文将从几何画板在中学教学中的应用、教师和学生应用几何画板时存在的问题等方面进行论述。
关键词:几何画板;中学数学;教学应用;应用情况
众所周知,在电子计算机迅速发展和普及的今天,信息技术已经渗透到各个领域,这其中也包含教育。在数学教育领域中,仅利用传统“粉笔+黑板”的教学模式很难满足教育现代化,因此,新课标提出信息技术与课程整合的理念以此来实现教育现代化,而将几何画板融入课堂教学未尝不是一种实现数学教育现代化的明智之举。然而如何将几何画板和数学课堂教学有效融合,使教学过程更加适应数学现实以及学生认知规律,需要当代数学教师进行深入的思考和不断的探索。
一、几何画板在中学数学教学中的应用
本节主要以案例分析的形式从代数和几何这两个方面出发介绍几何画板的教学应用。
(一)几何画板在代數教学中的应用
在数学学习的过程中有大量的代数公式,若学生都靠死记硬背,只知结论而不知过程,只“知其然”而不“知其所以然”,则不算真正获取知识。《义务教育数学课程标准》中曾指出:“有效的数学学习活动不能单纯地依赖记忆和模仿,动手实践、自主探索和合作交流是学生学习数学的重要方式。”使用几何画板推导代数公式进行教学,能够很好地体现这一理念。学生在与几何画板相融合的课堂中能够充分自主探索、合作交流,经历一个数学过程,从而真正获取数学知识。下面用教学案例来说明几何画板在代数教学中的应用。
案例1:用几何画板推导平方差公式a2-b2=(a+b)(a-b).
利用几何画板制作课件如下:
第一步,在几何画板上动态演示“边长为a的正方形中移除边长为b的小正方形”的过程,引导学生观察左边裁剪后地剩余部分图形的面积为a2-b2。
第二步,在几何画板上动态演示“左侧剩余部分图形重组为右侧矩形”的拼接过程,引导学生算出第一步操作中剩余部分图形的面积的另一表达形式(a+b)(a-b)(即矩形的面积)。
综上可得:a2-b2=(a+b)(a-b),即成功推导出平方差公式。
平方差公式是八年级上册因式分解章节的内容,该公式会频繁使用于相关分解因式、二次根式中的分母有理化、解一元二次方程的计算中,如果教师只是简单地给学生直接呈现该公式,会使学生难以理解、掌握和运用,这时,借助几何画板来动态演示该公式推导过程,可使学生通过回忆该公式形成的动态过程来理解、掌握该公式,也可使学生从整体上体会数形结合的数学思想方法。用几何画板能够推导的代数公式还有很多,比如推导圆面积公式、勾股定理、均值不等式等。
(二)几何画板在几何教学中的应用
中学几何教学主要有平面几何的教学和立体几何的教学,在这两类的传统课堂教学中,教师往往以“粉笔+黑板”的教学模式将几何公理、定理等传授给学生,然而这种教学模式很难呈现几何的直观和动态这两大特点,学生也往往难以理解。而几何画板可以很直观地展示几何图形并灵活地显示其动态变化过程,这无疑大大地提升了课堂教学效果和学生学习效率。下面就两个教学案例来分别说明几何画板在平面几何和立体几何教学中的应用。
案例2:请同学们动手操作几何画板,通过更改焦点数据,分析焦点对双曲线图像的影响。
利用几何画板制作课件如下:
在该课件中,利用几何画板进行动态演示:
问题一:请同学们猜想焦点横坐标数据a改变而b、c不变时,双曲线离心率e如何变化?
问题二:请同学们动手操作,在几何画板上改变焦点横坐标数据a,观察其对应的双曲线函数图像的渐近线如何变化?
问题三:在几何画板上更改数据,a>c>0(即)时为什么图像会变成椭圆?思考离心率e=0、0<e<1、e=1、e>1时,分别形成什么圆锥曲线?
探究焦点对双曲线函数图像的影响的推导过程看似容易,但对该阶段学生来说仅借助传统教学往往难以理解,故教师应充分利用几何画板进行参数变化、动态演示,充分让学生理解和掌握双曲线图形中焦点的影响,使其经历一种数学“再创造”的过程。
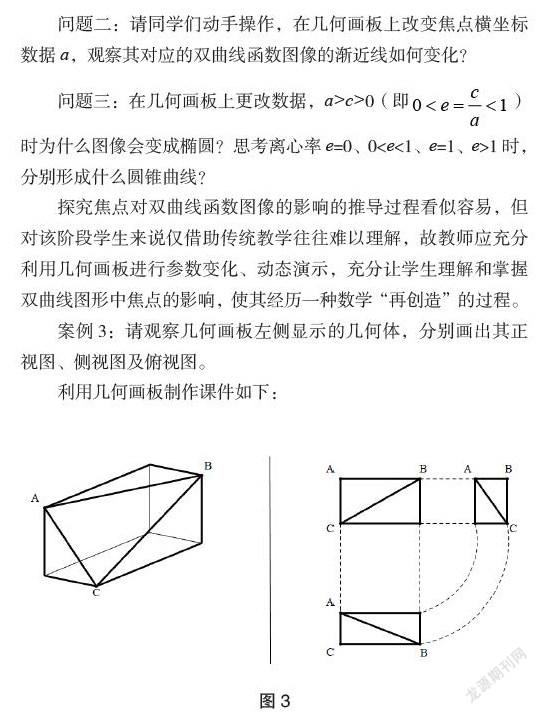
案例3:请观察几何画板左侧显示的几何体,分别画出其正视图、侧视图及俯视图。
利用几何画板制作课件如下:
在该课件中,插入“正视图”“侧视图”“俯视图”“恢复”“显示答案”这五个操作类动画按钮,利用几何画板进行动态演示:
第一步,点击“正视图”按钮就可以变换该几何体,经过一系列动态变换后,最终转变到从正面来观看该图形,得到一个含有一条对角线的矩形。
第二步,点击“恢复”按钮之后,再点击“侧视图”按钮旋转该几何体,经过一系列动态变换后,转变到从左侧来观看该图形,得到一个含有一条对角线的小矩形。
第三步,点击“恢复”按钮之后,再点击“俯视图”操作按钮变换该几何体,最终转变为从上方来观看该图形,得到一个含有一条对角线的矩形。
第四步,点击“显示答案”操作按钮,就会在课件的右侧显示其上述操作显示的正视图、侧视图和俯视图,即该几何体的三视图。
三视图是新课程高考的重要考察内容之一,使用传统的手工作图教学方法是很难直观地向学生呈现三视图的形成过程,因此,结合几何画板进行教学是十分有必要的。
用几何画板进行立体几何教学的例子还有很多,比如探讨空间轨迹问题、动态演示马鞍面等。随着新课程改革的不断深化,利用信息技术结合课堂教学培养学生空间想象能力已成为一个重要的教学理念,用几何画板来进行立体几何教学能够非常切合地践行这一理念,能够极大地帮助发展学生抽象思维能力。
二、几何画板在中学教学中的应用情况分析
本节将根据实际调查和参考相关研究,对几何画板在中学教学中的应用情况进行分析,主要研究对象分为教师和学生两部分,主要内容为教师和学生使用几何画板时存在的问题以及克服相应问题的对策。
(一)教师使用几何画板过程中存在的问题及建议
教师使用几何画板时主要存在两个问题:其一,教师使几何画板的水平普遍不高,无法将其灵活、自然地与课堂教学结合,从而难以发挥其优点。其二,教师们在结合几何画板进行课堂教学时常采用教师演示而学生观看的教法,这不满足佛莱登塔尔的学生“做数学”的教学思想,不能彰显新课标中强调培养学生基本活动经验的教育理念。
针对此,教师在运用几何画板时首先要熟悉软件,并在制定好教学设计后进行多次模拟授课,这样能很好地避免正式课堂中的教学失误或无法与课堂深层次融合的问题。同时,教师应运用几何画板结合活动情景,让学生基于自身知识经验背景来自主探究数学问题从而建构数学知识,这对培养学生数学建模、逻辑推理等数学核心素养有着积极意义。
(二)学生使用几何画板过程中存在的问题及建议
学生使用几何画板时主要存在两个问题:其一,我国使用几何画板教学以教师演示为主,学生的实际操作较少。其二,学生几何画板教学课堂,往往只注重几何画板呈现的表面形式,而忽视了对相关知识点或数学思想方法的学习。
针对此,教师应将几何画板使用的主动权交给学生,使其踊跃投入到探究性学习中。同时,学生在数学课堂上使用几何画板时应有意识地结合相关知识点进行思考并感悟蕴涵在该知识点中的数学思想方法,避免学习表面化。
三、结语
几何画板具有简明化、动态化和形象化的特点,其能把复杂的问题简单化、静止的问题动态化、抽象的问题具体化,从而优化中学数学课堂教学,提高教学效率。若教师能够正确、灵活地使用几何画板,则能更加有效地进行代数与几何这两个板块的教学;若学生能够充分使用几何画板,则能有效培养自身数学核心素养,贴合新课标的培养目标,成为具有创新意识、实践能力的新一代人才。
参考文献:
[1] 義务教育数学课程标准.中华人民共和国教育部[M].北京:北京大学出版社,2012.
[2] 张奠宙,宋乃庆.数学教育概论[M].北京:高等教育出版社,2004.
[3] 弗赖登塔尔.数学教育再探[M].上海:上海教育出版社,1999.
[4] 李敏.几何画板的实践与认识[J].高师理科学刊,2007,15(2):71-73.

