剪叉式高空作业车液压缸安装参数优化

吉 喆 董文龙 刘 涛 崔红韦

1北京起重运输机械设计研究院有限公司 北京 100007 2太原科技大学 太原 030024

0 引言

剪叉机构便于折叠，占用空间小，结构坚固，升降过程中能够保持较高的稳定性，广泛应用于各种仓储装卸场所。剪叉机构的液压升降装置受力复杂，叉臂与液压缸的运动速度为非线性关系，升降液压缸的安装位置很大程度上影响了机构的工作效率。殷彬[1]采用Ansys对剪叉式机构进行有限元分析，并得到应力分布情况，对机构进行优化设计；高希功[2]通过建立剪叉式升降机剪叉臂的受力分析理论，进而对剪叉臂的结构设计优化；郑玉巧等[3]利用 Matlab对液压缸最大推力的参数进行优化计算；高月玲[4]采用Ansys对剪叉升降机构进行疲劳寿命分析及结构改进。本文通过采用虚位移原理法，利用Design-Expert设计参数优化方案，综合考虑液压缸各安装参数之间的交互影响，选择出最优参数组合，为实际工程中剪叉机构的设计、评估提供了参考价值。

1 剪叉机构的力学模型

以往剪叉机构的力学模型与运动模型大多都是在计算其稳定性过程中采用动静法[5]与瞬心法[6]建立的。而虚位移原理应用功的概念分析系统的平衡问题，是研究静力学平衡问题的另一途径，也有许多学者采用该方法解决了剪叉臂受力分析的问题[7,8]。根据虚位移原理：在一个平衡系统中，作用于质点系的所有主动力在虚位移上所做的功与所有内力在虚位移上所做的功之和为0。即为

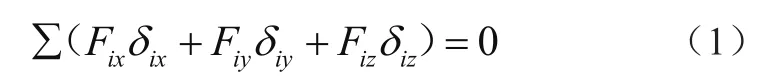
式中：Fix、Fiy、Fiz为作用于质点的主动力，Fi为在直角坐标系中的分量；δix、δiy、δiz为虚位移δi在直角坐标系中的分量。

为减少计算量以确保研究的顺利进行，将剪叉机构简化为图1所示的计算简图。

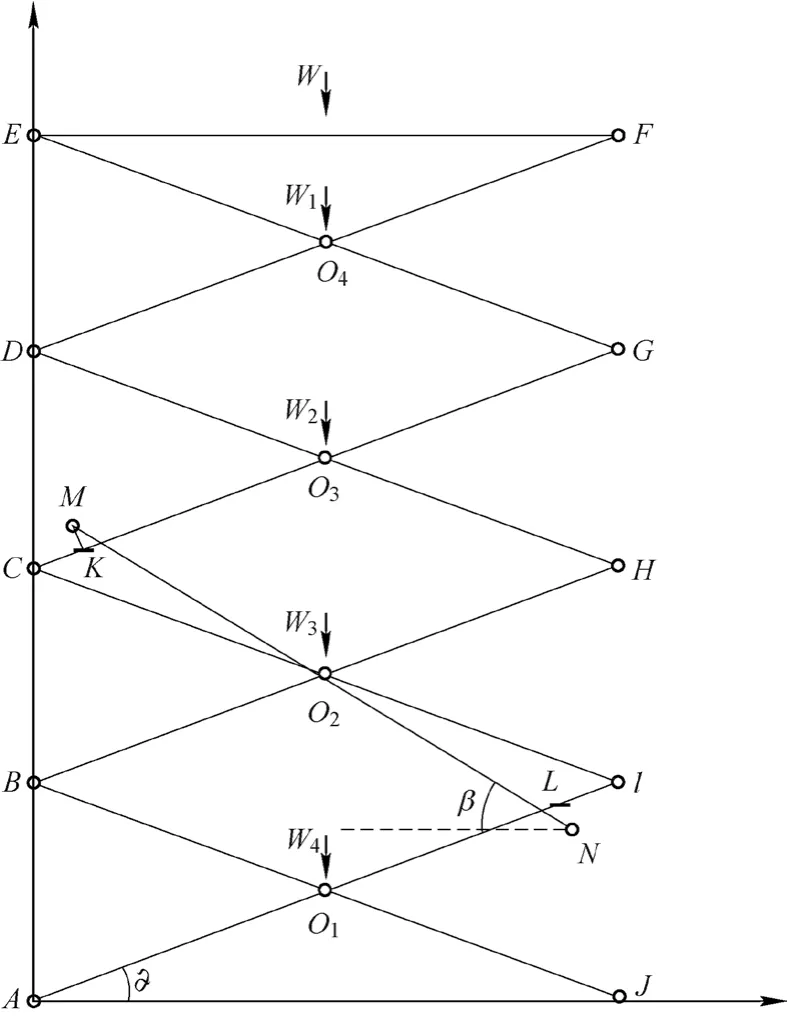
图1 剪叉机构受力简图

由虚功原理可得到整个剪叉平衡机构的虚功方程为

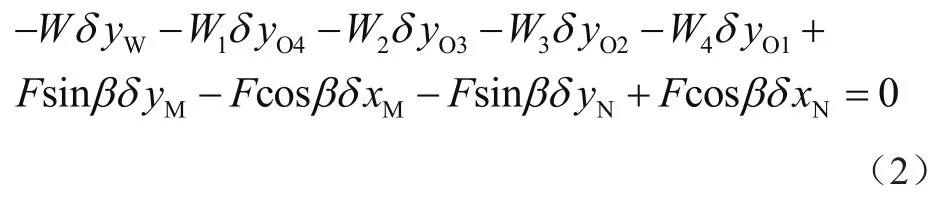
以A为坐标原点建立如图1所示的坐标系，确定各个质点系的坐标位置为

式中：L为剪叉臂长度，α为剪叉臂与水平面的夹角，β为该平衡位置时液压缸与水平面的夹角，r1为图1中MK、NL之间的距离，r2为LO1、KO3之间的距离。

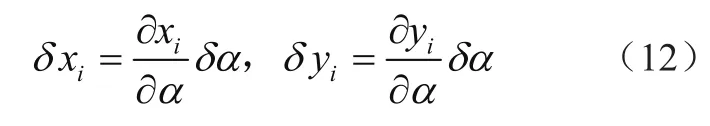
式中:xi，yi为各受力点的x和y坐标值。

将各式带入可得

由文献[9-11]与国家标准GB/T 9465—2018《高空作业车》[12]可查出四层剪叉机构的标准参数，如表1所示。

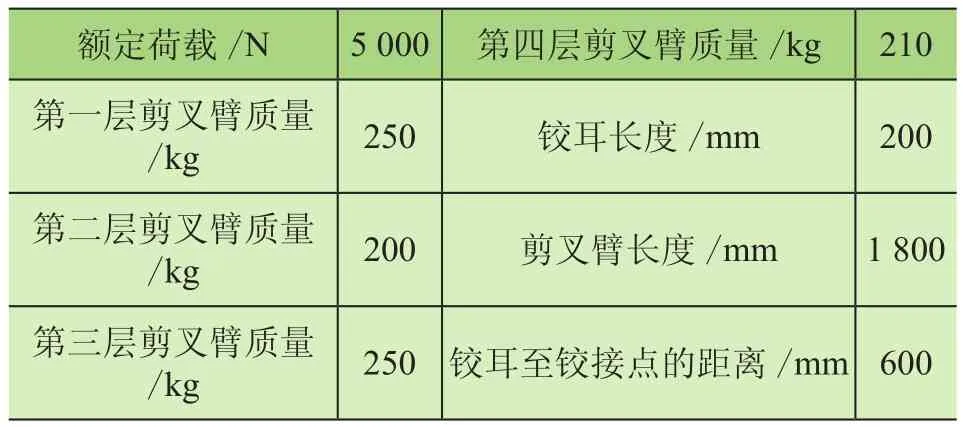
表1 标准剪叉结构参数

2 优化方案设计及模型分析

以上面的计算公式为理论依据，通过Design-Expert设计参数优化计算方案，以铰耳长度r1，铰耳至铰接点的距离r2，以及液压缸与水平面的夹角β为自变量，采用Box-Behnken设计方法，共进行17次参数计算，将液压缸受力F作为响应指标，通过前期的文献与实际调研确定如表2所示的水平因素编码表。

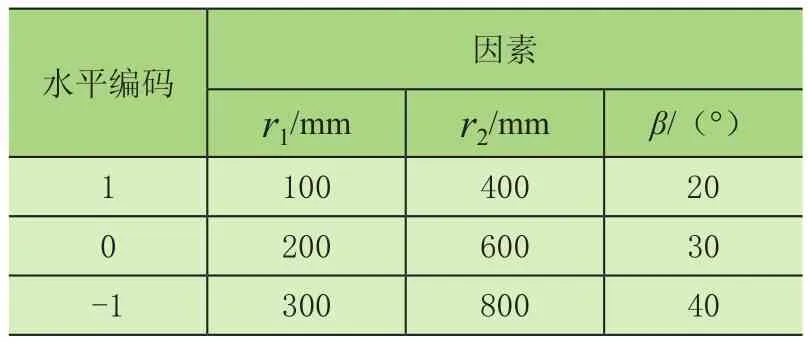
表2 因素水平编码表

响应指标F与各自变量之间的数学回归模型为

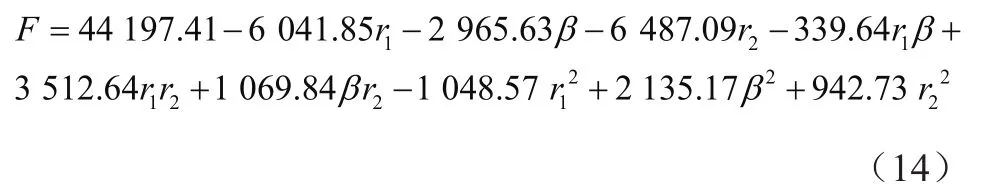
在Design-Expert后处理界面提取对液压缸受力分析时所产生的方差表，用于考量设计方法的可靠性，如表3所示。f与P值均能表现出模型的可靠性，f值在一定范围内越大越好，而P＜0.01表示该项极显著；P＞0.05表示该项不显著。

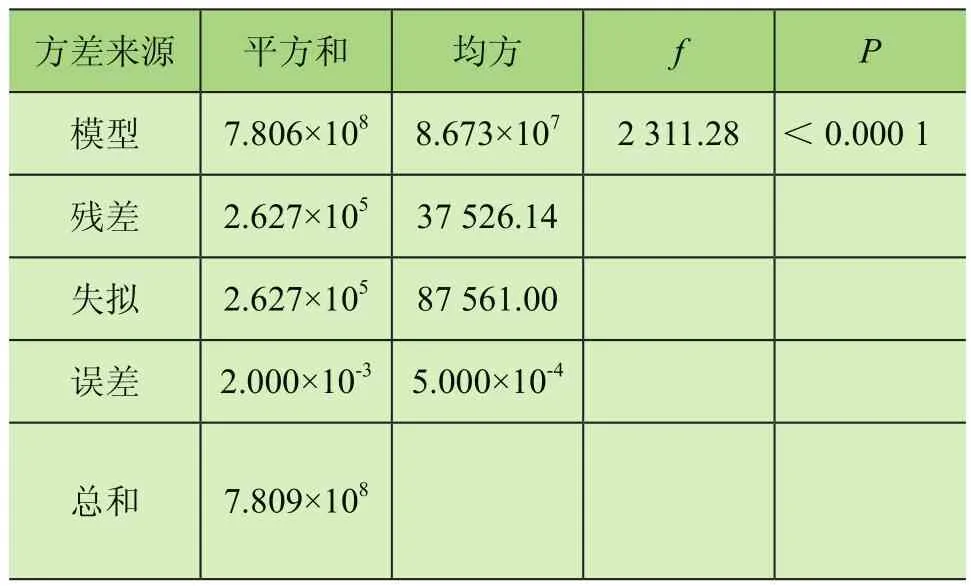
表3 液压缸受力回归方程方差分析表

由表3可知，模型P值小于0.000 1，表明模型高度显著，且液压缸的力F通过计算得来，故不存在失拟项的P值；其决定系数R2为0.999 7，与校正决定系数为0.999 2均接近于1，说明响应指标拟合的回归模型具有较高可靠性，对液压缸受力优化具有一定的参考意义。

3 安装参数对响应指标的影响

对回归模型的方差中P＜0.05，即交互影响显著的因素进行分析，如图2所示，铰耳到铰接点的距离一定时，液压缸受力随着铰耳长度的增加逐渐减小。液压缸角度在20°～40°的范围内，随着角度的逐渐增加，虽然液压缸受力有先减小后增大的趋势，但整体数值变化不大。

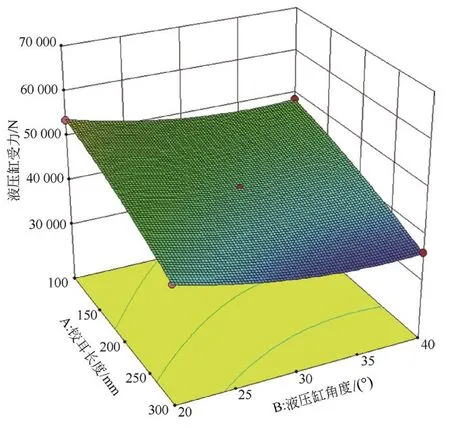
图2 r2一定，r1和β的响应曲面

如图3所示，将液压缸的角度固定在30°，液压缸受力随着铰耳到铰接点距离的增加逐渐减小，但变化趋势逐渐减缓，随着铰耳长度的逐渐增大，液压缸受力基本均匀减小。

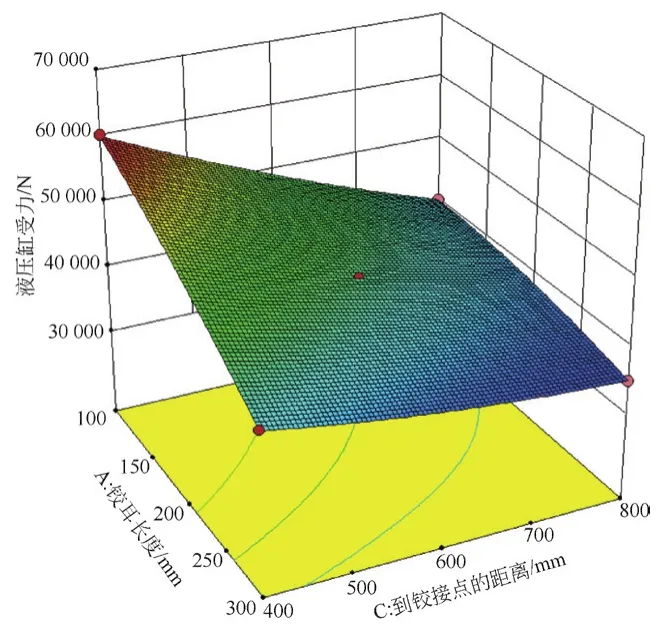
图3 β一定，r1和r2的响应曲面

如图4所示，保持铰耳长度不变，在一定范围内液压缸受力随着铰耳到铰接点距离的增大而减小，在到铰接点距离400～550 mm的区间内，液压缸受力随液压缸角度的增大而减小，在550～800 mm的区间内，液压缸受力随液压缸角度的增大先减小后增大。

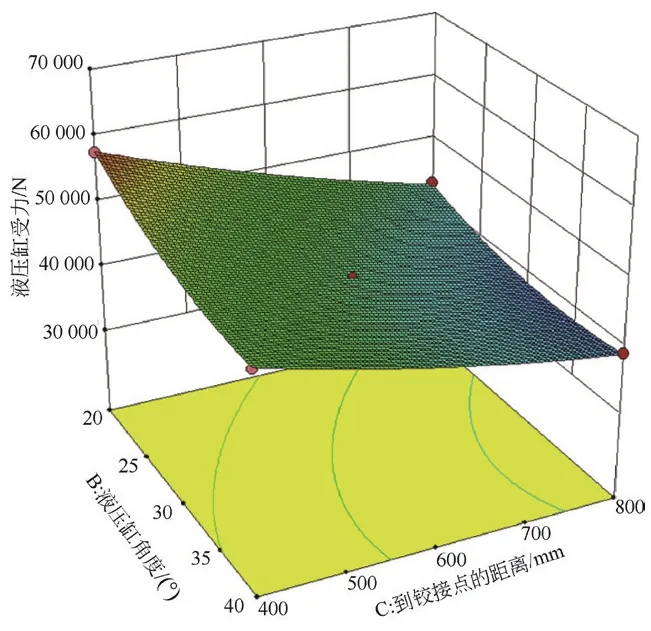
图4 r1一定，β和r2的响应曲面

4 参数优化及验证

由上述分析可知各自变量与响应指标之间的交互影响，使用Design-Expert中的Optimization功能，以液压缸受力最小为最优条件，将铰耳长度r1，液压缸角度β，铰耳到铰接点的距离r2规定在合适的范围内，得到最优参数组合r1=298.81 mm，β=38.49°，r2=773.25 mm，此时液压缸受力F=34 821.6 N。为确保优化参数的准确性将r1=299 mm，β=39°，r2=774 mm，带入液压缸受力公式得F=35 318.4 N，计算值与优化数值仅有1.4%的误差，说明两者的变化趋势一致，该优化方法对工程具有实际意义。

5 结论

本文以四层剪叉机构作为研究对象，对机构某一工作状态进行简化，采用虚位移原理法获取举升液压缸的受力表达式（2）；通过Design-Expert中的Box-Behnken设计方法，建立铰耳长度r1，液压缸角度β，铰耳到铰接点的距离r2之间的回归模型，并分析了三者对响应指标液压缸受力的交互影响；利用Design-Expert中的Optimization功能，以液压缸受力最小为最优条件，获得最优参数组合，且与实际计算误差仅有1.4%，表明该研究方法能作为设计和评估剪叉机构的参考依据。本文通过理论模型建立进行力学分析，与实际试验分析存在一定的误差，条件允许的情况下可在本文章研究的基础上添加试验或仿真探讨其工作参数的优化组合。