全国名校必修5 综合测试卷（A 卷）

■河南省汝阳一高 刘俊报

一、选择题

1.在△ABC中，若角A、B、C所对的边分别为a、b、c，则下列有关正弦定理及其变形错误的是（ ）。

A.a：b：c＝sinA：sinB：sinC

B.a＝b⇔sin2A＝sin2B

D.a＝b⇔sinA＝sinB

2.给出下列四个条件：①xt2＞yt2；②xt＞yt；③x2＞y2；④0＜。其中能成为x＞y的充分条件的是（ ）。

A.①② B.②③

C.③④ D.①④

3.若关于x的不等式x2－4x－2－a＞0在区间（1，4）内有解，则实数a的取值范围是（ ）。

A.（－∞，2） B.（－∞，－2）

C.（－6，＋∞）D.（－∞，－6）

4.如图1 所示，正方形一边上连接着等腰直角三角形，等腰直角三角形腰上再连接正方形，……，如此继续下去，得到一个树形图形，称其为“勾股树”。若某勾股树共有1023 个正方形，且最小的正方形的边长为，则最大的正方形的边长为（ ）。

图1

5.已知等差数列{an}的前n项和为Sn，若m＞1，且am－1＋am＋1－－1＝0，S2m－1＝39，则m等于（ ）。

A.39 B.20 C.19 D.10

7.如图2 所示，在平面四边形ABCD中，△BCD是等边三角形，AD＝2，BD，则△ABC的面积为（ ）。

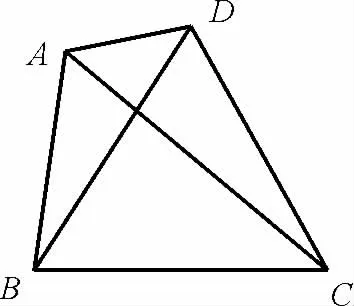
图2

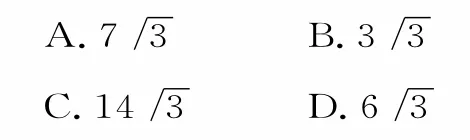
8.已知数列{an}的前n项和为Sn，且满足3a1＋32a2＋…＋3nan＝n（n∈N*），若对于任意的x∈R，n∈N*，不等式Sn＜x2＋ax＋1恒成立，则实数a的取值范围为（ ）。

9.已知数列{an}满足an＋an＋2＝2n（n∈N*），则数列{an}的前20项和S20＝（ ）。

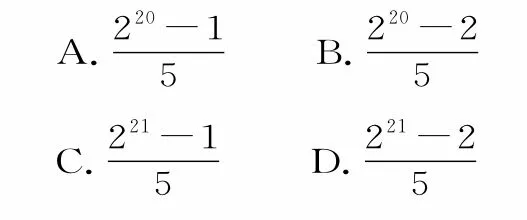
10.在△ABC中，角A、B、C所对的边分别为a、b、c，已知∠ABC＝120°，∠ABC的角平分线交AC于点D，且BD＝1。有以下四个结论：①＝1；②ac的最小值为2；③ac＋的最小值为2；④a＋2c＋ac的最小值为5＋。

其中所有正确结论的编号为（ ）。

A.①③④ B.②④

C.①③ D.①④

12.在钝角△ABC中，a、b、c分别是△ABC的内角A、B、C所对的边，∠A是钝角点G是△ABC的重心，若AG⊥BG，则cosC的取值范围是（ ）。

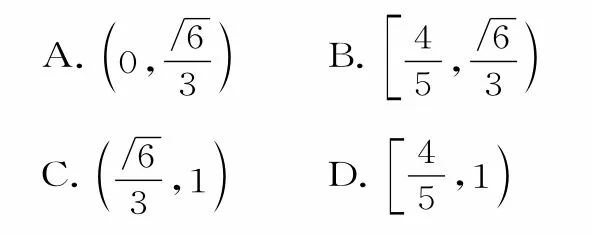
二、填空题

16.如图3，在△ABC中，∠ACB＝60°，点D在AB的延长 线 上，AB＝2BD＝，则CD长的最小值为____。

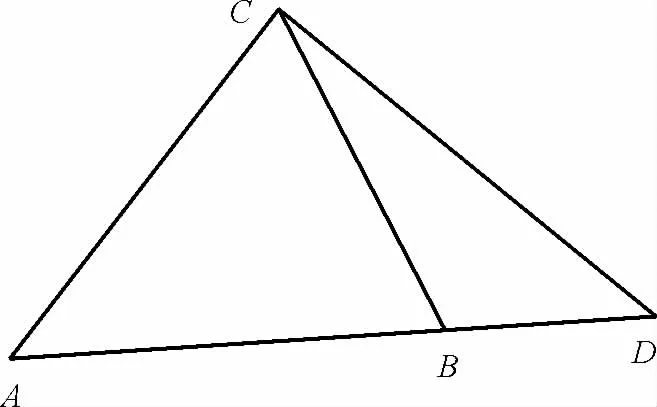
图3

三、解答题

17.在△ABC中，三个内角A、B、C所对的边分别为a、b、c，且c－b＝acosBbcosA。

（1）求角A的大小；

（2）若a＝1，求△ABC周长的范围。

“我不想提那次，看来你非要我说。那天清晨，第一笼包子刚刚出锅，来了几个执法人员，说是突击检查。看了营业执照、从业人员健康证；检查原料仓库和我的住所；还拿走了两个包子回去化验。临走时告诉我，今天不要营业了，如果包子化验出问题，不但要关门，还要追究我的责任。如没有问题，明天照常营业。”

18.在△ABC中，点D在边BC上，AB＝3，AC＝2。

（1）若AD是∠BAC的角平分线，求BD∶DC的值；

（2）若AD是边BC上的中线，且AD＝，求BC的大小。

19.已知函数f（x）＝x2－2（a＋1）x＋4a。

（1）若a＝，解不等式f（x）＞0；

（2）解关于x的不等式f（x）＜0。

20.设正项等比数列{an}的前n项和为Sn，已知S3＝21a1，且a2n＝。

（1）求数列{an}的通项公式；

（2）若bn＝，求数列{bn}的前n项和Tn。

21.已知数列{an}满足a1＝1，an＋1－2an＝2n－1。

（1）设bn＝，证明：数列{bn}是等差数列；

（2）记Sn为等差数列{an}的前n项和，若对任意的n∈N*，不等式k·2n－1－≤0恒成立，求实数k的最大值。

22.设数列{an}是公比q为正整数的等比数列，满足a1＋a3＝10，－a3＝8，设数列{bn}满足b1＝1，bn＋1＝。

（1）求{bn}的通项公式；

（3）记cn＝，n≥2，求c2＋c3＋c4＋…＋cn的值。