基于差分进化算法的不同浓度冰浆流动特性研究
邵佳栋,周文杰,郝 帅,许文柱,周延锁
(1.杭州电子科技大学能量利用与自动化研究所,杭州 310018;2.天津大学机械工程学院,天津 300072)
0 引言
中国的乳制品加工正在从量产转型为质产。为了减少乳品加工生产过程中的碳排放,提高乳制品质量,关键环节是冷却。冷却的目的是为了在高温杀菌后迅速降温以保证乳品的质量。对国内乳制品加工生产情况的调研发现[1],为了满足乳制品冷却需求,我国往往采用大型冷水机组来提供冷源。目前,集聚式冷水机组已经能够满足现阶段乳制品加工日益增长的冷源需求,但是该方法存在不可忽视的缺点[2]:(1)冷却速度慢且冷却过程中温度不稳定;(2)冷水机组频繁开停机使其寿命减少的同时用电量增加;(3)所需电功率大,增加了电网负荷;(4)制冷系统自动化程度低,生产效率低。
冰浆由一定体积分数的冰和冷水组成,其相变潜热较大,比冷水的蓄冷能力和制冷效果好。研究表明,冷水机组须增加80%~350%的流量才能达到与冰浆制冷系统相同的制冷效果[3]。同时,冰浆制冷系统中包括冰浆储存装置,该装置能够在夜间储存流态冰供白天使用,节省用电成本。因此,目前在某些领域冰浆制冷系统正在逐步代替传统的制冷装置,本文通过研究不同体积分数冰浆的流动特性,为冰浆制冷系统设计提供参考意见。
1 典型冰浆制冷系统
图1为一家奶酪加工厂冰浆制冷系统的示意图。该厂每天生产9万公斤奶酪。奶酪发酵剂冷却和乳清蛋白浓缩、过滤等过程的冷却负荷估计为每天2 546 kW·h。冷却负荷峰值出现在上午7:00,此时干酪发酵剂须从85℃降温到25.5℃,此过程需要265 kW的冷却负荷。峰值负荷仅在白天出现,只有1 h,厂内其他冷却需求使该时间内总峰值负荷达到396 kW,其余23 h中,总冷却负荷在56~148 kW间变化,占峰值负荷的40%以下[4],如图2所示。
为了降低负荷高峰,填补负荷低谷,使负荷曲线趋于平滑,安装了一个冰浆制冷系统,该系统由一个功率为106 kW的冰浆发生器和24.6 m3的储槽组成,能够储存763 kW·h的能量,如图1和图2所示。

图1 奶酪加工厂冰浆制冷系统示意图Fig.1 A schematic of the cheese processing ice slurry plant
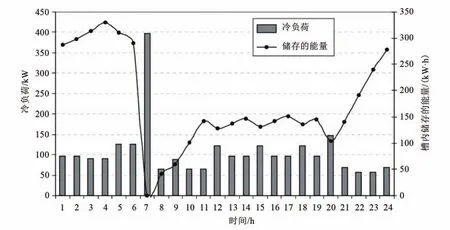
图2 24 h冷却负荷分布和储槽中的能量曲线Fig.2 Load profile and storage tank capacity over a 24-hour period
冰浆制冷系统连续运行,用7%体积分数的丙二醇初始水溶液生成5%~10%体积分数的冰浆。生成的冰浆被泵送到储槽,由于密度差异,冰晶和冰溶液分离并分别占据储槽的上部和下部。一个大约为0℃的冷冻溶液从储槽底部被泵送到换热器,“温暖”的溶液返回储槽,并通过喷雾喷头分布在冰晶层上。
冰浆制冷系统在不需要或需要较少冰浆时,冰浆发生器产生的冰浆被泵送到储槽中备用;当有冷却需求时,将冰浆从储槽中泵出,通过管道运输至冷却区域。王子龙等[5]的研究发现,流动过程中,冰浆会摩擦管道内壁产生压降,而压降会对系统的热容量和功耗造成影响,压降越大,系统的热容量越小,功耗越大。因此研究如何在满足制冷需求的情况下产生尽可能小的压降,对提高制冷效果和减少功耗具有重要意义。
2 冰浆湍流模型与算法
悬浮液在管内的流动分为三种模式:悬浮流、移动床和固定床,冰浆在管内的流动也分为这三种[6]。流动状态取决于流体自身的特性,而流体的特性是多种参数相互影响的函数。当冰浆在管道中运输时,由于其流动的复杂性,冰浆的可视化是困难的,其流型也难以控制。一些学者研究发现,可以通过转换速度对冰浆的流动状态进行分类:Wasp等[7]将从层流过渡到湍流的速度称为“过渡速度”;Shook等[8]把冰浆颗粒层开始形成时的速度称为“临界沉积速度”。
以临界沉积速度为特征,一些冰浆研究学者如Frei等[9]观察到,当冰浆速度低于临界沉积速度时,压降增加,载流体(NaCl溶液)无法携带流体中的冰颗粒,这时容易造成冰堵。因此要选取大于临界沉积速度的流速,使流体处于悬浮状态。值得注意的是:当临界沉积速度增加时,出现冰堵的可能性高。
由于冰浆在管内流动的复杂性,常常用经验函数来计算其临界沉积速度,常用的有[7]:

式中:g为重力加速度,9.8 m/s2;D为管道直径,mm;ρi为冰密度,kg/m3;ρs为溶液密度,kg/m3;
按照式(1)计算,8%质量百分数的NaCl溶液在50 mm管径下的临界沉积速度约为0.7225 m/s。许多不同的实验表明[10],冰浆在低的体积分数时表现为牛顿流体,在高的体积分数时则表现为非牛顿流体。对于等温流动,温度是恒定的,不考虑能量方程。这种流动的压降可以用达西-魏斯巴赫公式(Darcy-Weisbach)计算:
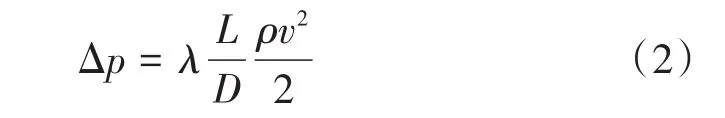
式中:λ为流体摩擦因子;L为管道长度,m;ρ为冰浆密度,kg/m3;v为冰浆的流速,m/s。Darcy-Weisbach公式充分反映了冰浆在管内的流动压降。
λ可以用不同的流体模型来描述,其中,Sasaki等[11]提出的宾汉姆模型被众多学者如Kauffeld等[12]采用。Marr等[13]认为冰浆是一种幂律膨胀流体。Snoek[14]更偏爱卡森模型。本文采用Reghem[15]提出的一种针对冰浆在换热器中流动的半经验公式:
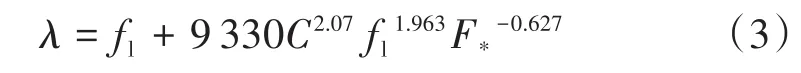
该半经验公式的适用条件为流速:v<4 m/s,冰浆体积分数:10% fl是Blasius提出的单相流在管内流动的摩擦因子: F*是弗劳德数,其计算公式如下: 随雷诺数Re不同,流体流动可分为层流和湍流[16]。对于冰浆制冷系统,为了保证生产过程的稳定与安全,须避免冰浆在管内的流动为移动床和固定床模式,防止冰堵现象出现对经济生产造成损失,因此只考虑冰浆的湍流状态。雷诺数的计算公式为: ηB为流体黏度,通常根据载液(冰浆)的浓度计算出悬浮液(固体颗粒分散于液体中的混合物)的有效黏度。已有许多不同的模型用于悬浮液黏度的测定,其中大多数实质上是爱因斯坦黏度方程的延伸[17]。本文采用托马斯方程[18]计算流体黏度: 式中:ηL为溶液黏度;为保证冰浆在管内为湍流,选取雷诺数为0.64×104~0.42×105。 采用海水冰浆(NaCl)作为研究对象,由于NaCl溶液密度与冰密度相近,因此采用线性加全方法来获得冰浆密度[19],公式如下: 根据式(8)作出图3。 图3 冰浆密度与冰浆体积分数和NaCl溶液密度的关系Fig.3 The relation between ice slurry density and ice concentration and NaCl solution density 从图3可以看出,随着冰浆体积分数的增加,冰浆密度减小。结合式(2)与式(3)~(8),给出冰浆体积分数、管径与压降的关系,如图4所示;流速、管径与压降的关系,如图5所示;冰浆体积分数、流速与压降的关系,如图6所示。 图4 管内达西压降与冰浆体积分数的关系Fig.4 The relationship between the flow pressure in the tube and the concentration of flow ice 从图4可以看出,随着冰浓度增大,管内达西压降不断增大。 从图5可以看出,随着流动速度增大,管内达西压降也不断增大。 图5 管内达西压降与流速的关系Fig.5 The relationship between the flow pressure and velocity in the tube 从图6可以看出,同时考虑冰浆体积分数和流速时,随着它们增大,管内达西压降也增大。 图6 管内达西压降与冰浆体积分数和流速的关系Fig.6 The relationship between flow pressure and ice concentration and flow rate in tube 管道输送能力可以由流体质量流量乘以补给线和返回线之间的焓变表示。冰浆在温度(T)下的焓变ΔH可以写成: 式中:Q为单位时间内的流量。 式中:t为时间,s;hice为冰的潜热,335 kJ/kg。 确定了流量即可计算流体携带的冰的制冷能力。当确定了制冷所需的能量时,就能通过改变速度来调整管内的达西压降。 冰浆是一种被用作热载体和用来储存能量的流体。冰浆系统的优化是对其具有产生温差、传热和储能部件的系统的优化。 冰浆流动过程优化由三个基本部分组成: (1)由Darcy-Weisbach方程获得冰浆流动过程中压降最小值; (2)获得影响压降最小化的冰浆体积分数和流速变化组合; (3)最终在满足制冷量要求前提下获得允许的冰浆体积分数和流速变化取值范围。 本文采用差分进化算法(DE)[20]作为最优化算法。DE算法是从自然界生物的遗传、变异、优胜劣汰的进化中感悟而发展的一门基于种群的搜索算法。算法由四部分组成:初始、交叉、变异和选择。利用DE算法,产生可能的初始冰浆体积分数、流动速度组合,经过交叉、变异两个操作筛选出满足要求的组合,再进一步筛选,最终一步步逼近优化值,四个步骤的详细过程和结果如下。 目标函数为Darcy-Weisbach方程,使达西压降尽可能的小;变量选择为冰浆体积分数和流动速度;约束条件为10%~30%的冰浆体积分数、0.722 5~3 m/s的流动速度以及满足一定要求的制冷量。 (1)初始化种群,在DE中,种群由个体组成,每个个体可以表示为: 在初始化阶段,确定最小边界xmin和最大约束xmax,之后,每个个体被初始化,如式(12)所示。 式中:i,j为自变量;NP为种群规模,取50;CL为染色体长度,本次模拟中表示冰浆体积分数和流速两个变量,取2;rand[NP,1]为产生一个NP行1列的矩阵;xmin和xmax为变量的最小值和最大值。 经过上述步骤,产生了一个初始种群X[x1,x2],其中x1为冰浆体积分数,x2为流动速度来储存每一代的解。 (2)交叉 交叉操作是生成子个体的第一部分,每个子体的代表为: 按如下方式创建: CR表示交叉概率,0.1。例如,将X矩阵中的随机两组解“冰浆体积分数10%,流速1 m/s”与“冰浆体积分数20%,流速2 m/s”中冰浆体积分数或流速交换,变成“冰浆体积分数10%,流速2 m/s”与“冰浆体积分数20%,流速1 m/s”,就能使数据选取更具随机性。 (3)变异 DE有三个主要的操作符:交叉、变异和选择。变异操作符是生成子个体的第二部分,也是DE算法中最重要的一部分。此处Ur1,G,Ur2,G,Ur3,G代表从交叉过后的种群中随机选择的三个个体,通过变异算子突变个体与父个体结合生成新的子个体[21]。 每个突变个体如下所示: F为变异概率,0.4;r1,r2,r3在种群中随机选取且r1,r2,r3和i互不相等。为保证交叉变异后产生的新个体仍然满足约束要求,根据式(9)为冰浆优化加入制冷量前提,为个体插入边界约束条件后对新个体再次筛选,若不满足约束,则返回过程(2)重新进行流程。得到V矩阵,其中储存了经过一轮筛选过后既满足变量取值范围又满足制冷量需要的冰浆体积分数和流速组合。 (4)选择 选择运算符是DE过程的最后一个操作符,这个运算符选择一些将成为下一代种群的个体,其基础是比较父个体和子个体的适合度值。如果父个体的适应度值大于子个体的适应度值,则在下一代种群中父个体继续存在,子个体被淘汰。否则,父个体被替换为子个体。下一代个体的选择: 将变异得到的子代代入Darcy-Weisbach方程得到相对应的压降值,通过比较保留每代中压降值小的个体组成新的父代种群进行下一次迭代筛选。随着进化代数的增加,种群必然收敛于最优解,即得到满足制冷前提的最优冰浆体积分数和流速配比。 图7为DE算法流程图。 图7 DE算法流程图Fig.7 DE algorithm flow chart 图8是制冷量为250 kW时的寻优结果,在19.22%的冰浆体积分数和1.922 8 m/s的流速下可以既满足制冷前提,又对管道有最小的压力,表1、图9为对不同制冷前提冰浆流动的数值模拟。 图8 管内达西压降随迭代次数增加的寻优结果Fig.8 Optimization results of flow pressure drop in pipe with the increase of iteration times 表1 不同制冷需求下的冰浆体积分数和流动速度配比Tab.1 Ice slurry concentration and flow velocity ratio for different refrigeration requirements 图9 制冷量随流速与冰浆体积分数变化的寻优结果Fig.9 Optimization results of cooling capacity with flow rate and ice depth 结合表1和图9可以看出,在低制冷量需求时,冰浆体积分数和流动速度的组合差别不大;随着制冷量增加,(1)冰浆体积分数和流速的增加率保持稳定;(2)冰浆体积分数的增加比小于流速的增加比,这反映出冰浆体积分数对压降的影响大于流速。 本文以海水冰浆为研究对象,采用Darcy-Weisbach方程与DE算法,得到了几组在管径50mm、8% NaCl溶液、不同制冷量下的冰浆体积分数和流速配比,该结果可在一定程度上减小冰堵现象的发生、减少系统功耗和提高制冷效果。通过模拟发现,当所需制冷量为250 kW时最佳冰浆体积分数为19.22%且流速为1.922 8 m/s,此时既能满足制冷要求又能减少系统功耗,提高制冷效果。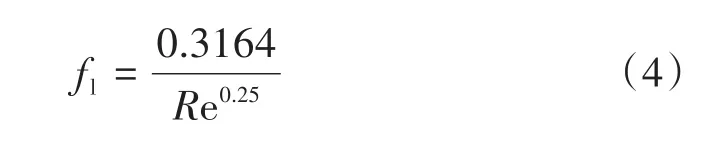
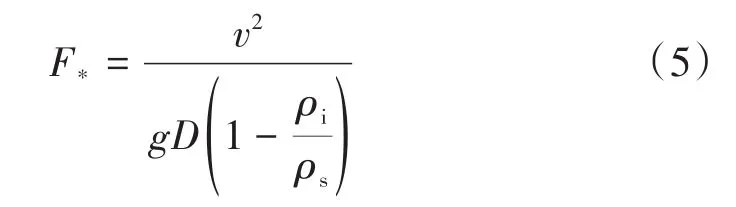









3 数据处理与分析



4 结论

