间歇性和滞后效应策略的不连续神经网络同步分析

赖艺芬，宾红华，陈 超，黄振坤

(集美大学理学院，福建 厦门 361021)

0 引言

近年来，不连续激活函数的神经网络被广泛地研究并应用到许多领域，如冲击机、干摩擦、电源电路等[1-2]。除了对该类神经网络的平衡解和周期解的稳定性和收敛性[3-11]进行研究之外，人们也逐渐关注其同步控制问题。同步在科学与工程领域中的应用越来越多：文献[12]将分数阶同步系统应用到数字密码学中，得到一个安全的密钥系统；文献[13]研究了一类分数阶混沌系统的同步问题，获得主动控制下的认证加密方案；文献[14-15]分别将同步应用到基于出生日期的仿射密码、分数阶眼镜王蛇混沌系统中。同步应用到连续系统及混沌系统的成果已经很多，但关于不连续系统的同步应用却很少。关于复杂网络同步，人们提出很多方法和实验技术，如状态反馈控制[16]、自适应控制[17-18]、滑模控制[19]、非线性反馈控制[20]、模糊系统的控制[21]、间歇性控制[22]等，但是很少有文献同时考虑到间歇性和滞后效应控制。受现有文献的启发，在Filippov解和广义李雅普诺夫稳定性理论的框架下，本文结合滞后效应和间歇性的控制策略，获得不连续神经网络的同步控制准则。

1 问题描述

考虑N个耦合节点的神经网络系统，其状态方程为

(1)

网络(1)的孤立节点可表示为

(2)

其中：x(t)=(x1(t),x2(t),…,xn(t))T为神经网络的状态向量;f(x(t))=(f1(x1(t)),f2(x2(t)),…,fn(xn(t)))T为神经元的输出，是不连续函数向量。

关于不连续函数和连接矩阵参数，本文作如下假设。

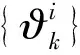
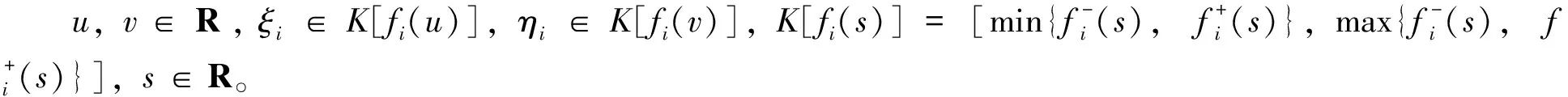
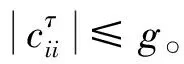
引理1[3]若假设1、假设2满足， 则非连续系统(2)任意初值问题至少有一个定义在[0,+∞]上的解[x,γ]。

根据文献[19]中初值问题的定义和引理2.10，系统(1)至少有一个解[xi(t),γi(t)]。

关于神经网络(1)的同步定义如下。

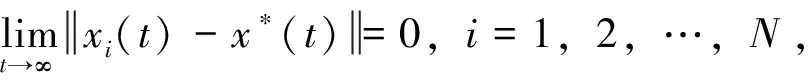
控制神经网络(1)的描述如下：

(3)

其中ui(t)是后文中将要设计的控制输入。

(4)

设计基于间歇性和滞后效应策略的控制器

(5)

2 主要结论

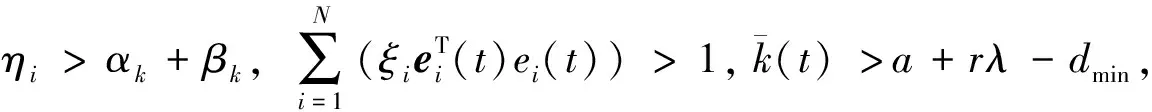
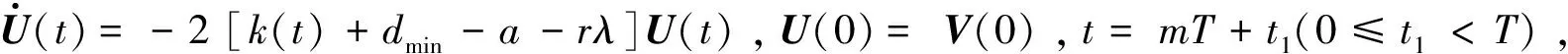
文献[18]利用广义李雅普诺夫方法，设计状态反馈控制器ui(t)=-kiei(t)-ηisign(ei(t))，实现了不连续激活的线性耦合时滞神经网络的同步。在文献[18]的基础上，本文给出了间歇性控制策略，并运用李雅普诺夫稳定性理论和微分方程比较定理加以证明，所得结果具有更好的适用性。

3 数值摸拟

为了验证以上的理论分析，本节给出一组参数来进行数值模拟。

例1 考虑3个耦合节点，每个节点是1维的神经网络。网络的孤立节点方程为

(6)

显然，网络(6)满足假设1与假设2，L=1，N=0.08。3个耦合节点的时滞神经控制网络为

(7)

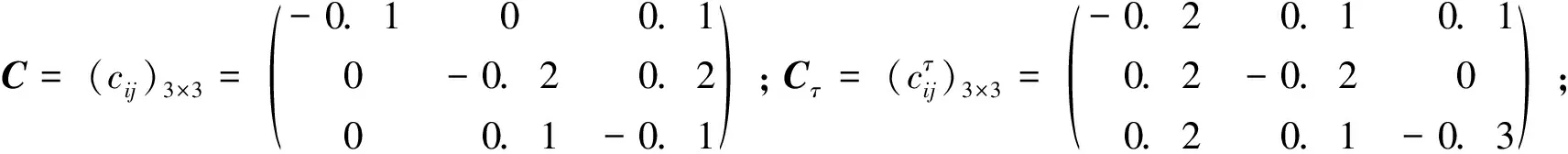
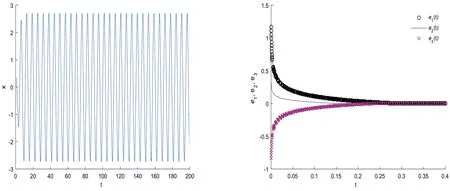
4 结论

本文提出了一种结合间歇性和滞后效应的控制策略，探讨了一类线性耦合不连续神经网络的同步问题，所得的结果是文献[18]的补充与推广，具有很好的适用性。数值仿真验证了理论结果的有效性。针对文中这类线性耦合不连续神经网络，是否有更好的同步控制策略,可以作为今后的一个研究方向。