基于迁移学习的湿法烟气脱硫系统出口SO2浓度预测研究

王力光， 贠勇博， 朱保宇， 司风琪

(1. 大唐环境产业集团股份有限公司特许经营分公司， 南京 211100；2. 东南大学 能源热转换及其过程测控教育部重点实验室， 南京 210096)

SO2是大气中的主要污染物之一。我国电力依赖于煤炭资源，燃煤电厂排放的SO2给环境造成了很大的影响。国家环保发展规划要求持续推进电力行业SO2减排工作，控制SO2排放成为发电企业面临的重大课题[1]。目前，我国电厂大多使用湿法烟气脱硫技术，其中采用石灰石-石膏湿法脱硫的机组占脱硫总装机容量的85%左右[2]。因此，对石灰石-石膏湿法烟气脱硫系统出口SO2浓度进行实时监测尤为重要。燃煤电厂布置了大量的烟气分析监测仪器，例如利用烟气连续排放检测系统(CEMS)对脱硫系统出口烟气中的SO2浓度进行监测，但这只是对SO2排放量的单一结果反馈，并不能反映脱硫系统过程参数与出口SO2浓度之间的关系；另外，CEMS在线分析仪表维护保养复杂，价格昂贵，受外界环境等因素影响较大，往往会出现测量结果漂移的现象[3]。

为了监测SO2排放量，优化湿法脱硫系统的运行参数，需要建立脱硫系统出口SO2浓度预测模型，掌握脱硫系统过程参数与出口SO2浓度之间的关系。目前，主流的建模方法分为机理建模和数据驱动建模。燃煤电站脱硫系统运行过程具有动态、非线性和时变等特性，机理建模较为困难，且模型精度往往难以满足工程实际的要求；但随着计算机、传感器、数据存储和通信等技术快速地发展，数据驱动建模越来越多地应用到电站脱硫系统中。与传统机理建模方法不同，数据驱动建模通过数据清洗和挖掘来获取系统特征参数间的关联特性[4]，并不需要深入了解系统复杂的机理特性，能够满足复杂热工过程设备或系统的建模需求[5-7]。因此，笔者建立了基于最小二乘支持向量机(LSSVM)的脱硫系统出口SO2浓度预测模型。

通常，数据驱动建模必须满足训练和测试数据服从相同分布的假设，主要从对象自身的数据中挖掘知识，但在当前超低排放的背景下，为了满足排放要求，石灰石-石膏湿法脱硫系统高负荷运行时常常将吸收塔浆液循环泵全开运行，减泵运行的方式较少[8]，这使得减泵运行方式下的运行数据较少，并且与浆液循环泵全开状态下的脱硫系统运行数据的分布差距明显。因此，以浆液循环泵全开状态下的运行数据为主要训练样本建立预测模型。

由于训练数据与减泵运行数据分布存在差异，在减泵运行时的SO2浓度预测效果较差。为了解决数据分布差异带来的模型泛化能力较差的问题，笔者采用迁移学习的思想，将已存在丰富运行数据的浆液循环泵全开状态(即源域)的知识通过一定的方式迁移到数据量不足的减泵运行状态(即目标域)。现有的迁移学习主要可归纳为两大类：(1)实例重加权[9-10]，这是一种基于样本的迁移学习方法，它根据某种加权技术重用源域的样本，进行迁移；(2)特征匹配，即利用子空间几何结构进行子空间学习[11]，或者通过分布对齐来减少域之间的边缘(或条件)分布差异，属于基于特征的迁移学习方法。其中，实例重加权方法针对较为相似的数据迁移效果较为明显。

因此，首先考虑到脱硫系统特性参数的相关性及系统的非线性，建立了基于LSSVM的脱硫系统出口SO2浓度预测模型。其次，针对运行数据分布变化的场景，从样本迁移的角度，采用基于实例重加权的核均值匹配(KMM)迁移学习方法建立了加权LSSVM模型，实现了不同浆液循环泵组合运行方式下脱硫系统出口SO2浓度的预测。

1 基于KMM样本加权的LSSVM预测模型

1.1 基于LSSVM的预测模型

LSSVM是一种改进的支持向量机(SVM)算法。针对SVM计算复杂、效率较低的问题，LSSVM利用二次损失函数将SVM的寻优过程变为求解线性方程，简化了模型寻优迭代过程。经过不断地研究和改进，LSSVM已广泛应用于工程实际中非线性回归估计等问题[12]。

1.1.1 LSSVM原理和计算过程

给定任意的训练集D=(xi,yi),i=1,2,…,l，其中，l为样本数量，输入数据xi∈Rm，输出数据yi∈Rm，m为维数，LSSVM定义的回归函数J为：

(1)

约束条件为：

yi=wTφ(xi)+b+ei

(2)

式中：w权重向量；γ为惩罚参数；e为近似误差，e=[e1,e2,…,el]T；φ(·)为非线性映射函数；b为偏置。

相应的拉格朗日函数为：

b+ei-yi]

(3)

α=[α1,α2,…,αl]T

式中：α为拉格朗日因子。

基于Karush-Kuhn-Tucker(KKT)条件，可通过w、b、ei和αi的偏微分获得方程解：

(4)

联立消除w和ei，得到

(5)

式中：I为单位矩阵；y=[y1,y2,…,yl]T；1=[1,1,…,1]T；Ωij=φ(xi)Tφ(xj)=K(xi,xj)，K(·)为核函数，i,j=1,2,…,l。

最后，得到LSSVM的回归模型为：

(6)

式中：y(x)为LSSVM得到的回归函数，该预测模型采用线性核，主要参数为惩罚参数γ。

1.2 KMM实例迁移算法

针对源域和目标域分布差异的问题，基于样本的迁移学习算法[9-10]大多着眼于对源域和目标域的分布比值进行估计。具体如下：

在d维数据空间，有ntr个独立同分布的训练样本Xtr={xi|i=1,…,ntr}从概率密度函数(PDF)为ptr(x)的分布采样而来；而nts个独立同布分的测试样本Xts={xj|j=1,…,nts}从另一个分布pts(x)采样得到。假设pts(x)相对于ptr(x)是连续的(即ptr(x)=0时，pts(x)=0)，则密度比β(x)计算式为：

(7)

KMM算法通过在再生核希尔伯特空间(RKHS)中，最小化加权训练数据分布β(x)ptr(x)和测试数据分布pts(x)之间的最大均值差异MMD为：

MMD2(F,β,ptr,pts)=

‖Ex-ptr(x)[β(x)φ(x)]-Ex-

pts(x)[φ(x)]‖2

(8)

式中：‖·‖是L2范数,RKHS即φ(x)，x→F;Ex为期望。

若核空间是通用的，并且pts(x)相对于ptr(x)是连续的，则式(8)的解β(x)收敛到pts(x)=β(x)ptr(x)。

使用Xtr和Xts的经验平均代替期望，最小化MMD距离相当于最小化相应的二次规划问题，即

(9)

β=[β1,β2,…,βl]T

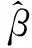
Kxtr,xtr=K(xi,xi′),xi,xi′∈Xtr

(10)

Kxtr,xts=K(xi,xj),xi∈Xtr,xj∈Xts

(11)

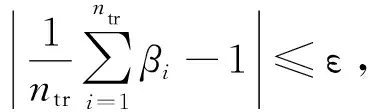
第一个约束给出了密度比βi的范围，反映了pts(x)和ptr(x)之间的分布差异。第二个约束则是对β(x)的正则项。

式(9)给出了具有线性约束的凸二次规划问题，可以通过二次规划解算器计算得到最优解。建模过程中使用MATLAB软件工具箱中较为成熟的“interior-point-convex”算法作为二次规划解算器。

1.3 基于KMM的样本加权LSSVM

在LSSVM模型建好后，当面对测试样本Xts与训练样本Xtr分布出现差异的场景时，该模型的泛化能力变弱，预测精度降低。此时，从样本迁移的角度，通过KMM算法求解得到训练样本Xtr的权重β(x)，再根据式(6),得到样本加权的LSSVM模型为：

(12)

综上所述，整个基于KMM样本加权的LSSVM算法步骤见图1。

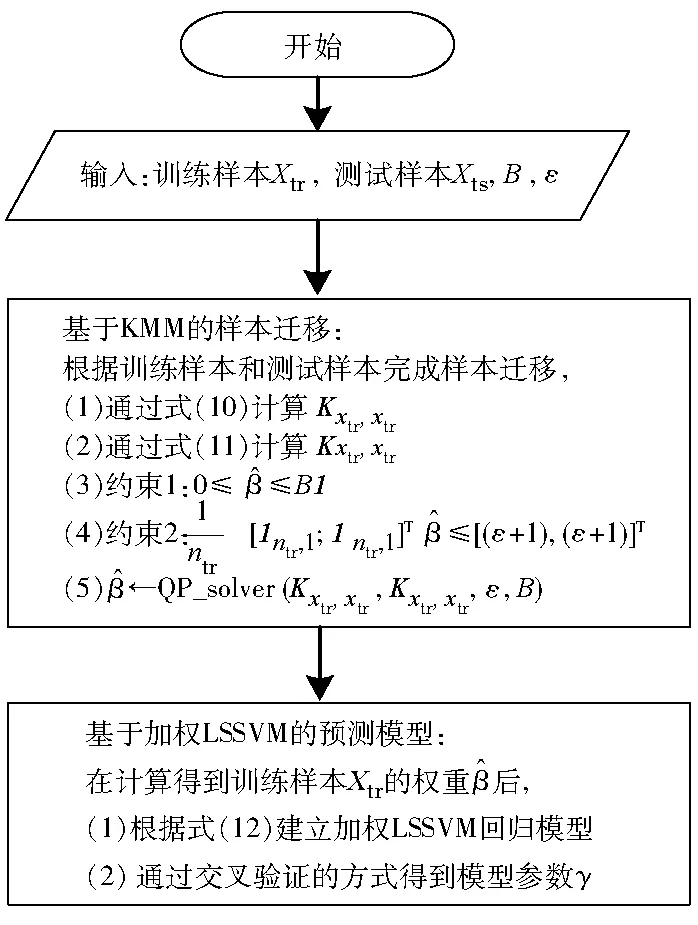
图1 基于KMM样本加权的LSSVM算法步骤流程

2 脱硫系统出口SO2浓度预测

在当前超低排放背景下，为了满足环保要求，即使是在低负荷运行工况下，脱硫系统的浆液循环泵多数也是开启的，甚至全开，影响了运行经济性。出现该问题的根本原因是未能掌握不同浆液循环泵组合运行方式下脱硫系统出口SO2浓度信息，从而采用了保守的运行方式。因此，笔者将建立机组实际运行负荷范围内不同浆液循环泵组合方式运行下的脱硫系统出口SO2浓度预测模型，为机组在不同工况下的浆液循环泵优化调度提供指导。

2.1 模型参数

以某600 MW机组为研究对象，石灰石-石膏湿法脱硫系统的脱硫过程大致为：来自锅炉的烟气经烟气系统和引风机增压后，通过烟气换热器降温，降温后的烟气自下而上进入吸收塔，而塔内的石灰石/石灰浆液自上而下进行喷淋，通过逆流混合的方式，进行一系列物理和化学反应并伴随着持续的热交换，从而脱除烟气中的SO2；脱硫后烟气中的液滴经过除雾器去除，烟气再经烟气换热器增加温度，达到温度要求后，通过烟囱排入到大气之中；经反应后吸收SO2的石灰石浆液(主要成分为CaSO3)流入脱硫塔底部的浆液池中，而增氧风机鼓入的空气将对其进行强制氧化，生成可二次利用的石膏(主要成分为CaSO4)。

脱硫系统中的主要运行参数之间存在着密切的相关性，结合整体脱硫过程，选取入口烟气流量(x1)、入口烟气氧体积分数(x2)、入口SO2浓度(x3)、入口烟尘质量浓度(x4)、入口烟气温度(x5)、石灰石浆液供给流量(x6)和浆液pH(x7)为模型输入参数，脱硫系统出口SO2浓度为输出参数，且采用折算浓度，即将原始数据中的SO2排放量折算到基准含氧体积分数(6%)下。

2.2 数据处理

该石灰石-石膏湿法脱硫系统有4台浆液循环泵，其主要设计参数见表1。从该600 MW机组厂级监控信息系统(SIS)中选取1个月的运行数据，采样周期为60 s。

表1 浆液循环泵主要性能参数

电厂SIS采集的数据往往受到通信和传感器故障等影响，因此需要对采样的数据进行清洗。目前，采用iforest孤立点检测算法对异常数据进行剔除。此外，机组运行工况发生较大变化时，模型变量的统计特性也会发生变动，因此数据预处理还包括了对稳态数据的筛选。笔者选用锅炉负荷为特征变量，对采集的数据进行了稳态判定和筛选。

经过数据处理后，一共筛选出5 412组稳态数据。进一步分析后发现，主要包含了2种浆液循环泵组合运行方式数据：4 415组4台浆液循环泵运行(简称4泵运行)数据，937组3台浆液循环泵运行(简称3泵运行)数据。对这2种运行方式的数据分布进行分析，结果见图2。

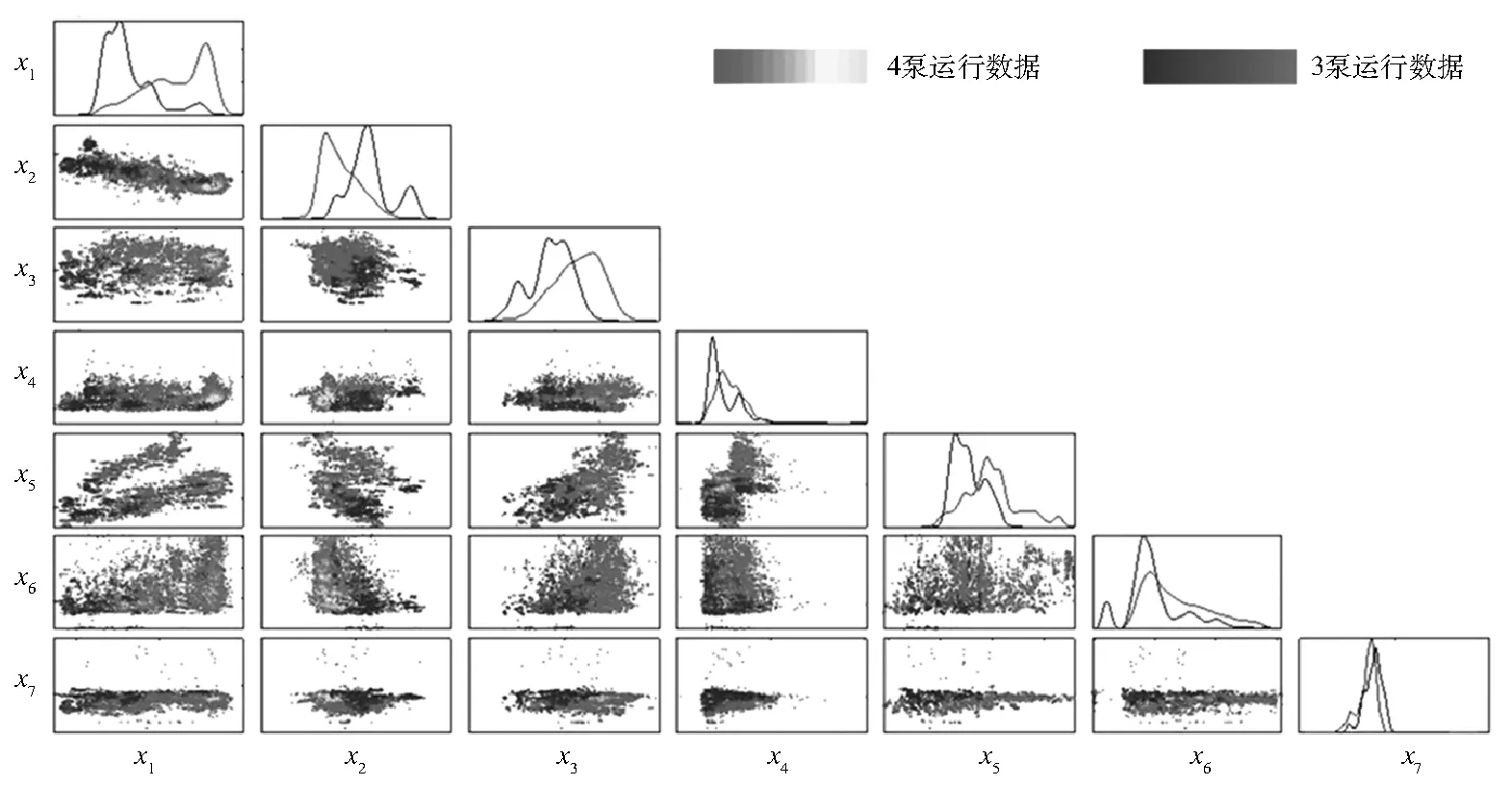
图2 不同浆液循环泵组合运行方式的数据分布对比

从图2可以看出：4泵运行和3泵运行的数据分布存在一定差异，并不满足数据驱动建模要求的数据独立同分布的假设。若以4泵运行数据作为训练样本进行建模，对3泵运行结果进行预测，预测精度将明显下降，即模型的泛化能力不足；若以3泵运行数据进行建模和预测，又因训练样本过少，模型发生过拟合的现象，无法进行预测。因此，采用迁移学习的思想，将数据量较大的4泵运行数据(源域数据)通过样本重加权的方式迁移至与3泵运行数据(目标域数据)相同分布上，减少不同浆液循环泵组合运行方式下的模型参数分布差异，提高模型的泛化能力。

2.3 模型建立

在数据处理和分析后，针对拟要解决的问题，建立以下几种场景的模型，设计并进行对比试验。

场景1：只采用3泵运行的少量数据进行建模训练和测试，观察模型的预测精度。

场景2：只采用4泵运行的训练数据进行建模，用3泵运行的数据进行测试，观察预测结果，以验证样本迁移的必要性。

场景3：利用4泵运行的数据，考虑样本迁移，建立了基于KMM样本加权的LSSVM预测模型，并对3泵运行的数据进行预测，分析预测结果。

场景1和场景2的模型都只是LSSVM预测模型，场景3涉及KMM算法进行样本迁移的过程，其中KMM算法用到的核函数选择高斯核函数。3种场景中都采用交叉验证(CV)对LSSVM模型参数进行寻优，3种场景的参数寻优结果分别为18、7、11。

为了定量评价不同场景下的模型性能，利用回归模型中使用广泛的均方根误差(RMSE)与决定性系数R2来衡量模型预测值与实测值之间的偏差，其计算公式分别为：

(13)

(14)

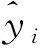
2.4 结果分析

场景1下LSSVM预测模型对训练样本和测试样本的预测结果见图3。由图3可以看出：由于3泵运行的时间短，数据较少，工况覆盖面较窄，因此模型的预测精度较低，3泵运行训练时的R2为0.817，测试时的R2只有0.576，无法满足工程实际需要。

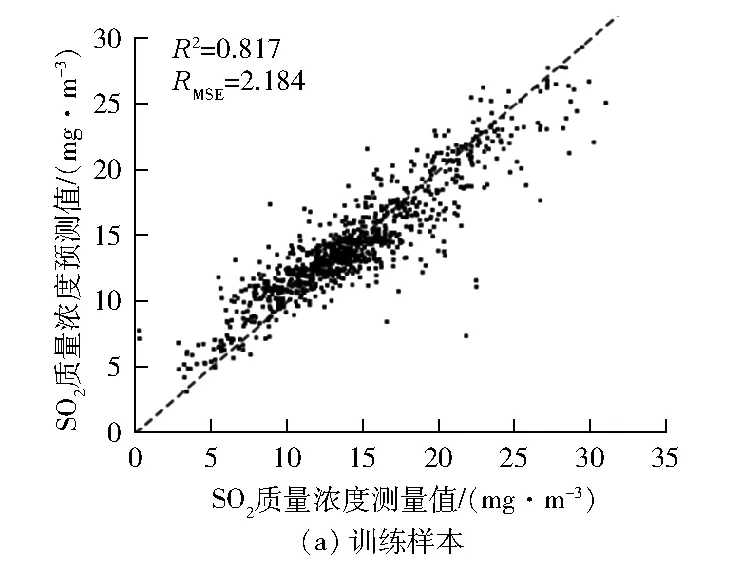
图3 场景1下脱硫系统出口SO2质量浓度测量值与模型预测值对比

场景2下的模型预测结果见图4。

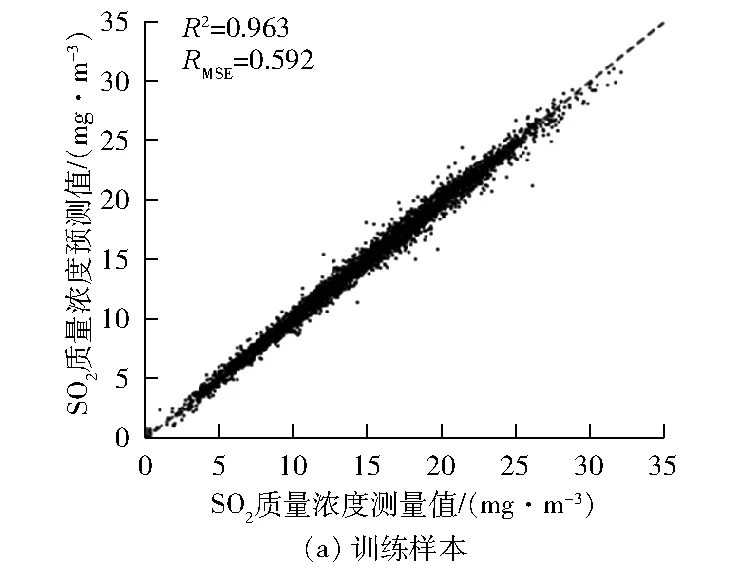
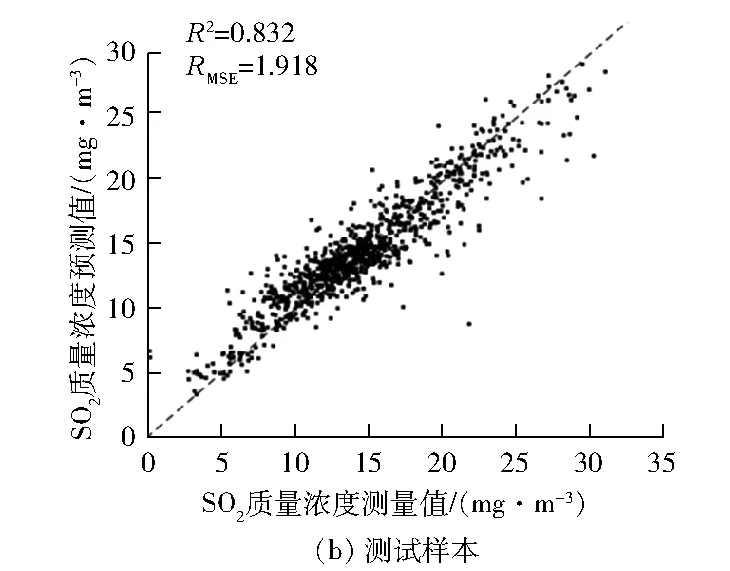
图4 场景2下脱硫系统出口SO2质量浓度测量值与模型预测值对比

从图4可以看出：由于4泵运行数据样本较多，训练模型的精度较高，R2达到了0.963，但是若以基于4泵运行数据建立的模型来进行3泵运行结果的预测仍存在一定问题，测试时的R2为0.832。分析原因为虽然这2种模型的脱硫运行机理一样，但是通过图2可以发现，由于浆液循环泵组合运行方式不同，模型的特性参数呈现出不同的工作特性；同时，4泵运行数据与3泵运行数据边缘分布有着明显的不同，直接采用这种方式建立预测模型，无法达到预期效果，模型存在训练过拟合的现象。

因此，在场景1和场景2的基础上，进一步设计得到场景3，采用基于KMM样本加权的LSSVM对不同浆液循环泵组合运行方式下的脱硫系统出口SO2浓度进行预测，结果见图5。

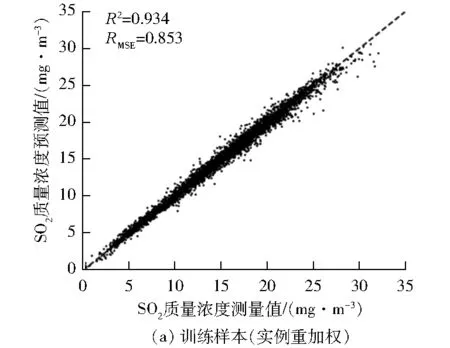
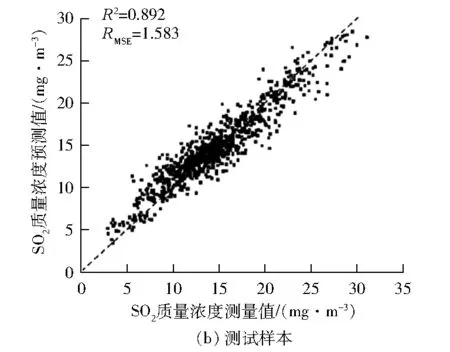
图5 场景3下脱硫系统出口SO2质量浓度测量值与模型预测值对比

由图5可以看出：场景3的改进模型对3泵运行测试样本的预测效果明显优于场景1和场景2，样本测试时的R2从0.576上升到0.892。

综上所述，采用笔者所提出的基于KMM样本加权的LSSVM建模方法(场景3)，一方面实现了不同浆液循环泵组合运行方式之间的样本迁移，使得4泵运行的模型参数被成功地迁移到3泵运行的数据分布之中，另一方面通过样本加权与LSSVM方法融合，实现了模型预测精度和泛化能力的提升。

3 结语

以脱硫系统SO2出口浓度预测为研究对象，针对不同浆液循环泵组合运行方式下模型特性参数边缘分布差异带来的模型泛化能力较差的问题，采用实例重加权的迁移学习策略，建立了基于KMM的样本加权LSSVM预测模型。以某600 MW机组脱硫系统现场运行数据为样本进行了模型训练和测试，通过3种场景的对比试验，结果表明：相较于采用单一运行方式数据建立模型(如：训练3泵运行数据后测试3泵运行时的SO2浓度，R2为0.576；训练4泵运行数据后测试3泵运行时的SO2浓度，R2为0.832)，所提出的模型(基于4泵运行数据的KMM样本加权LSSVM预测模型)在测试时的R2为 0.892，明显提高了不同浆液循环泵组合运行方式下的脱硫系统出口SO2浓度预测精度，而且预测模型的泛化能力也明显增强。