低压配电网无功补偿容量和选址方法

雷司宇 谭 聪 彭海超 王 赫 孙冰南

（国网吉林省电力有限公司松原供电公司，吉林 松原 138000）

在不久的将来，低压配电网络中将纳入大量可再生能源的，即配电网中的非线性分量将进一步增加并复杂化，这也使得复杂的低压配电网电压崩溃事件发生的概率大幅度提升[1]。无功补偿装置能够为配电网络的鲁棒性提供有效的支撑，从而使配电网能够稳定高效地供电，成为未来配电发展计划过程的关键设备。

目前，由于配电网络架构复杂，在多类型故障工况下对无功补偿设备的定容和选址的科研成果相对较少。文献[2-3]针对两种不同的故障工况提出了无功补偿的方法，但其只是考虑了故障工况下的功率占比，没有将配电网潮流中的故障线路对非故障线路的详细纳入计算范围，进而造成无功波长设备安装后非故障线路的功率波动较大的现象。如何在配电网络中对无功补偿装置进行精确的定容与选址是一个亟待解决的问题[4-5]。

为了攻克配电网故障量化复杂以及无功补偿设备选址定容的关键挑战，本文将构建配电线路故障态的无功补偿设备的电气化模型，通过多目标优化，求解最优的无功补偿方法，充分运用精英策略的自适应遗传算法求解无功补偿电气化模型，以实现加快算法的收敛速度，尽快达到全局最优的目标。通过IEEE-14 节点经典算例的仿真验证，证明了其可行性。

1 低压配电网无功模型设计

1.1 低压配电网的裕度

低压配电网的运行裕度大体涵盖了容量裕度、电压裕度以及功角裕度，本文充分考虑了上述基础配电网的裕度指标，特殊考虑了无功补偿裕度，当低压网络出现多类型故障后，相关的裕度指标能够直观地体现全网的稳定性。

1.1.1 有功功率的裕度建模

所构建的配电网有功功率裕度数学模型为：

公式中，Pmax与Pmin分别是有功的最大值和最小值Pi是潮流计算值。

1.1.2 无功功率的裕度建模

所构建的配电网无功功率裕度数学模型为：

公式中，Qmax与Qmin分别是无功的最大值和最小值Qi是潮流计算值。

1.1.3 电压的裕度建模

所构建的配电网电压裕度数学模型为：

公式中，Vmax与Vmin分别是无功的最大值和最小值Vj是j 节点电压计算值。

1.1.4 配电网络的裕度函数构建

配电网络的电压、有功功率以及无功补偿装置的裕度是低压配电网的关键的裕度指标，但在多类型故障状态下，删除指标需要进行加权，形成备点网络裕度函数，即综合指标。

1.2 低压配电网的线路损耗

低压配电网中的线路损耗是关键的经济性指标，在配电系统正常工况下，线路损耗大体涵盖了有功损耗以及无功损耗。在低压配电网络中，各个支路的电抗通常远超电阻，也就是无功损耗要远超有功损耗，即采用无功补偿的方式来抑制无功损耗，能够有效提高配电网络的传输效率，对无功补偿技术的研究具有深远的意义。在配电模型中，将线损作为经济指标，其表达式为：

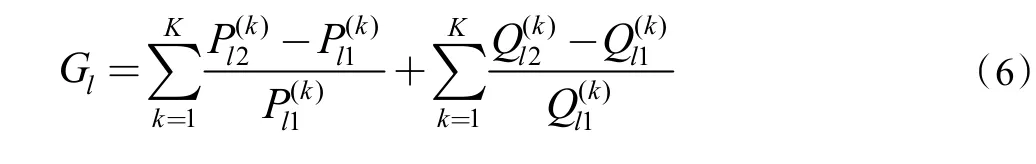
式中，Pl2和Ql2分别是无功补偿后有功功率与无功功率的总损耗，Pl1和Ql1为无功补偿前的有功功率与无功功率的总损耗。因此，Gl表示系统补偿前后的线损降低率。

1.3 多类新能源接入的补偿成本

多类新能源的补偿成本是配电网在正常工况下的关键指标，多源接入成本大体针对接入节点在稳态工况下的有功输出，补偿成本大体针对接入节点处的补偿装置的安装成本以及运行成本。在低压配电网络中，多源接入节点设置为PV 节点，所配置的无功补偿装置的目的即为将该节点的电压位置在1 p.u.。多源接入成本的表达式为：

式中，Pk是第k 个多源接入节点相配电网注入的有功功率，Qk是第k 个多源接入节点安装无功补偿装置的补偿值，CP是多类型新能源的发电成本，Gct是配电网补偿成本，Cg1和Cg2是分别是无功补偿装置安装前后的新能源发电费用。

1.4 目标函数

本文所构建的无功补偿装备选址定容综合目标函数表达式为：

式中：M是低压配电网络的稳定裕度，Gl是低压配电网络的线损，λ 是各级的权重。

1.5 约束条件

1.5.1 配电网络的潮流约束

配电网络的潮流是描述配电系统在某一特定时刻的运行工况关键参数群，主要包括了有功、无功、电压、相角等关键参数。由于电力系统是强非线性的，计算步骤繁琐，本节运用PQ 分节法记性相关计算，相关的潮流公式为：

式中，Pbus是全部接入节点向配电网络注入的有功，Qbus是全部接入节点所配置的无功补偿装置容量，Vm是配电网电压峰值，θm是功角，（10）与（11）的实质是，配电网络有功、无功、电压、相角等关键参数的平衡。

1.5.2 配电网络的线路约束

式中，Pg是多源接入节点的有功注入功率，Qg是多源接入节点的无功补偿容量，Vl是负载节点的电压，θl是功角负载节点的功角。

1.5.3 配电网络的经济约束

由1.5.2 节可以得出，各个节点的无功补偿值越高，配电网络的电压稳定性越强，配电系统受到多类型故障的扰动越小，但相关的投入成本也随之提高，所以考虑经济性约束后，其表达关系式为：

式中，Qloc是无功补偿装备的安装的地址，当Qloc=1 时，证明该节点配备的了无功补偿装备，当Qloc=0 时，证明该节点无无功补偿装备，Qcap是无功补偿装置的规划设计容量，CW 是无功补偿设备的选址后的安装费用，CP是单位容量的建设成本，Csum是总投资额。

2 低压配电网络的补偿求解算法

在配电网络N-1 故障时计算得出最优的无功补偿设备的选址定容方案，由于配电网络的数学模型的复杂度，本文拟运用蒙特卡洛方法对配电网络进行运算与仿真，该方法是通过若干次仿真的统计数据而形成的，需要预设各个支路的故障概率，在每一次的计算或仿真中仅设置某一条线路发生故障，并有效开断，通过多次的仿真计算，能够使整个模型的故障概率逐步靠近配电网的实际预设值。具体步骤如下：

（1）预设配电网各条线路的故障概率，以及总仿真计算的次数。

（2）建设配电网络仿真计算模型，配置相关的计算方案，对各条线路的故障类型进行配置。

（3）开始进行仿真，每次仿真仅有一条线路发生一种类型的故障，对每次仿真计算的结果进行记录，关键需要记录当次仿真的无功补偿装备的选址定容状态，以及相关目标函数的计算结果。

（4）重复进行（3），直至达到了（1）设定的总仿真计算的次数，统计各个线路多类型故障的选址定容状态，根据结果设计最后的低压配电网无功补偿配置方案。

最后使用配电网精英自适应遗传算法进行多轮迭代，确定最优选址规划的决策变量以及容量规划的决策变量。

3 算例分析

本文应用IEEE-14 的经典拓扑结构对所提出的无功补偿设备选址定容方案进行验证，配电网拓扑结构如图1 所示。图中，节点1 是平衡节点，节点2/3/6/8 是多类型能源的接入节点，其他节点为负荷节点。仿真所应用的参数如表1 所示。

图1 采用IEEE-14 节点的配电网络

表1 仿真所应用的参数

总投资额与补偿容量的对应关系如表2 所示，总的投资额对应不同的选址定容方案，但补偿的地址仍集中在接入节点1/2/3/6 附近，这证明了IEEE-14 样例中，接入节点添加的无功补偿装置能够有效地提高配电网络的稳定裕度。

表2 仿真所应用的参数

故障工况下的采用无功补偿设备的节点对应的目标函数经济的指标均为1，并与总投资额为100 时的选址定容方案进行比较。补偿后的结果如图2 所示，配电网络中各个支路中的目标函数基本均得到了较大的提升，尤其是1 号节点。此外针对2/3/4/5/6/14 节点的无功补偿能够使与其连接的2/3/4/5/6/7/17号支路的目标函数得到优化。这说明了对配电网的无功补偿能够充分提升其综合目标函数。

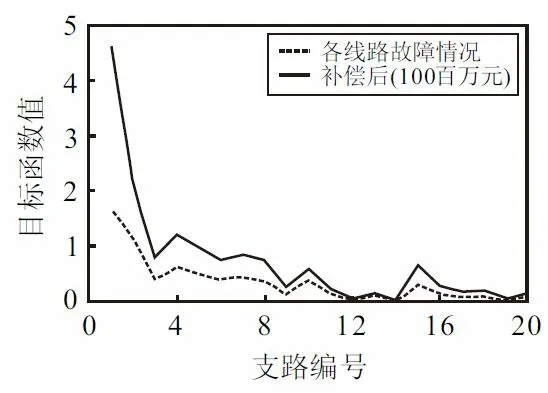
图2 无功补偿前后的目标函数对比

4 结论

本文面向低压配电网络N-1 的故障工况，充分运用配电网的多类型指标，在经济性约以及电气化的约束下，提出了低压配电网无功补偿设备的选址定容策略。详细分析了配电网络的潮流约束以及总投资额决定的安装数量约束，在保证全网鲁棒性的前提下，降低了设备投入的成本，以及配电网络的线损，再次与精英遗传算法相结合，设计了最终的选址定容方案。该方案通过了IEEE-14 节点经典算例的仿真计算，具有一定的可行性与应用价值。