基于几何代数理论的转子堆叠装配多目标优化

涂建波，李震，葛浩田，刘亮，刘洪慧

大连理工大学 机械工程学院，大连 116024

转子是航空发动机的重要部件，其装配质量对航空发动机的整体性能有着重要影响，同心度和初始不平衡量是评价总装质量的重要参数[1]，转子在高速旋转运动时，初始不平衡量直接影响总装的振动特性。由于转子无法避免在制造上的误差，在多级转子装配过程中，其误差不断传播和积累，最终可能使装配后多级转子的同心度和初始不平衡量超出工艺要求范围，降低航空发动机的可靠性和寿命。

转子堆叠预测理论[2-4]在应用上已经有比较成熟的经验，堆叠预测系统(Part measurement and Stacking Prediction system, PSP)是应用于航空发动机高压压气机转子装配过程中的一种先进的测量与预测装配技术。在转子装配前, 针对转子自身的测量数据，利用堆叠预测系统计算出最佳装配方案，保证转子装配后同心度的最小化，在进行大量装配时，既可以提高转子装配质量也显著提高了装配效率。随机装配时不考虑安装相位对转子精度的影响，即转子不做任何安装相位优化直接对转子进行安装。随机装配无法保证转子整件同心度和初始不平衡量大小，容易令转子质心与回转轴线的距离较大，使得转子整体初始不平衡量非常大，加剧了整机的振动，这是极其恶劣的一种情况。优化装配并非采用简单的逐级最优堆叠装配方案，而是综合考虑装配后转子整体状态，合理调整各级转子的安装相位，令各级转子质心与回转轴线的距离较小，使转子整件的同心度和不平衡量达到最优状态，从而提高转子的装配质量。随机装配和优化装配效果如图1所示，其中C1、C2、C3为各级转子质心。

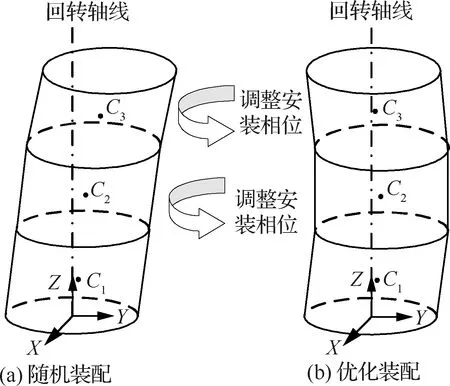
图1 装配示意图Fig.1 Assembly schematic

在多级转子装配几何误差积累和传播方面，目前已经做了大量的研究。Yang等[5]提出了柱形零件装配的误差传播和控制，阐述了多级转子装配时误差的来源和传播。Whitney等[6]建立了基于齐次矩阵变换的误差表示方法，此方法不仅可以表示零件间的位姿关系，还可以表示装配后部件的几何误差。Zhang等[7]提出了精密装配时零件几何误差建模方法，该方法考虑了装配结合面几何误差对装配精度的影响。Mantripragada和Whitney[8]基于机械装配中的状态转移模型提出了统计控制理论使装配误差最小化。在国内，曹茂国[9]采用powell算法对转子各级盘安装边进行了工艺装配优化设计，减小作用在轴颈上的力和力矩。李立新等[10]提出基于遗传算法的优化理论提高了多级转子安装相位优化的计算效率。琚奕鹏等[11]总结了多级转子同心度、垂直度与不平衡量的叠加机理及装配参数对不平衡量的影响关系。

由堆叠装配的特点可知，总的装配方案数目随着转子级数增加呈指数型增加，因此对计算效率要求较高。在多级转子装配建模方面，通常采用齐次矩阵变换。随着几何代数的发展，尤其是在李洪波[12]提出共形几何代数之后，几何代数得到了进一步的完善和发展，几何代数在机器人领域[13]、机构运动学方面[14-15]的应用越来越广泛，采用几何代数处理刚体的旋转问题[16]与传统方法相比具有一定优势，利用几何代数进行计算更加高效[17]。

本文基于几何代数[18]理论建立各级转子的误差传递模型，取代传统的齐次矩阵变换方法。综合考虑转子同心度和初始不平衡量，并基于遗传算法对转子进行多目标优化，为航空发动机装配工艺设计提供指导。

1 基于几何代数理论的误差传递模型

1.1 几何代数基本定义及运算

设{e1，e2，e3}是R3的自然基底，定义几何积eiej为

并且运算满足分配律和结合律，三维空间几何代数有23=8个基，其中正交基G={e1，e2，e3e1e2，e2e3，e2e3，e1e2e3=I}张成一个8维的线性空间。G1={e1e2,e2e3,e3e1}张成3维的子空间，其元素称为双重矢量(Bivector)，e1e2e3=I称为伪标量(Pesudoscalar)且eiI=Iei，eiejI=Ieiej，其中i，j=1,2,3。

在三维欧式空间中取2个普通矢量a、b；令a=a1e1+a2e2+a3e3，b=b1e1+b2e2+b3e3；a、b的几何积ab为

式中：a·b表示矢量的内积运算；a∧b表示矢量的外积运算。

三维空间中旋转问题计算形式。例如：矢量a绕矢量b逆时针旋转角度θ形成矢量a′。则

1.2 几何代数和齐次矩阵计算效率对比

所以c为

由c的表达式可知旋转算子转化为指数相加的形式大大降低了运算量。同理，基于齐次矩阵进行旋转变换时，令a=[ax,ay,az,0]T，b=[bx,by,bz,0]T，c=An…A2A1a；其中，Ai如式(1)所示。然而计算机计算An…A2A1时，为逐步相乘的计算形式，因此当进行大量的矢量旋转操作时，齐次矩阵计算方法同几何代数计算方法相比计算量大大增加。

令a=[1,1,1,0]T，b=[1/3,2/3,2/3,0]T，每次旋转角度θi=π/2，当n=100 000，150 000，200 000时，计算时间如表1所示。测试实验在3.4 GHz、 酷睿i5-7500处理器、8 G内存的计算机平台，由Python3.7编程完成。

(1)

如表1所示，随着旋转计算次数增加，2种计算方法所用时间均呈不断增大的趋势，但齐次矩阵计算方法用时较长，耗时增加幅度较大；几何代数计算方法用时较短，且随着计算次数的增加，耗时增加幅度较小。这是由于旋转算子优先进行指数相加，相对于矩阵乘法运算，计算量大大降低。因此，当进行大量旋转运算时，几何代数计算方法更加高效。

表1 计算方法对比Table 1 Comparison of calculation methods

1.3 转子堆叠误差传递模型

1.3.1 基于几何代数的坐标系变换

取三维空间中的3个正交基向量{e1,e2,e3}表示一级转子底面坐标系的3个坐标分量。记一级转子下端面坐标系{F1}={e1,e2,e3,0}，且圆心与坐标原点重合。一级和二级转子上下端面坐标系变换如图2所示。

令γx1、γy1、γz1为一级转子上下端面的旋转参数，R1为一级转子上端面坐标系相对于下端面坐标系变化的旋转算子，则一级转子上端面和下端面坐标系分别为

{F1}={ei,0}i=1, 2, 3

(2)

(3)

dx1、dy1为径向误差，dz1为高度误差，则一级转子上端面坐标系位置矢量为

P1=dx1e1+dy1e2+(dz1+H1)e3

(4)

式中：H1为一级转子的高度。

当二级转子安装相位为θ1，一二级转子配合面的旋转算子为r1时，则二级转子下端面坐标系为

图2 坐标系变换示意图Fig.2 Schematic diagram of coordinate system transformation

(5)

(6)

当dx2、dy2为径向误差，dz2为高度误差时，二级转子上端面位置矢量为

(7)

以此类推，当N级转子装配时，各级转子上下端面坐标系如式(8)和式(9)所示：

(8)

(9)

(10)

(11)

(12)

1.3.2 同心度和初始不平衡量计算方法

同心度定义为各级转子端面圆心和参考轴线在同一平面上的重合程度，为方便衡量同心度的优劣，利用各级转子端面圆心到参考轴线的距离大小即不同心误差来衡量转子同心度优劣水平。

转子组件不同心误差可以利用各级转子上端面圆心位置矢量与基向量e3的外积值来计算，并取其最大值。当多级转子装配时，由于转子本身存在几何误差，随着转子组件数目增加，转子组件不同心误差不断积累使得转子组件的不同心误差呈逐渐增大的趋势，如图3所示。

图3 转子组件不同心误差Fig.3 Misalignment error of rotor assembly

装配后k级转子组件不同心误差为

δk=max(P1∧e3,P2∧e3, …，Pk∧e3)

(13)

转子整体不同心误差为

δ=δN

(14)

转子不平衡是由于转子部件质量偏心或转子部件出现缺损造成的故障。不平衡的原因分为以下几种：转动件本身形状不对称、加工制造上的公差、组装安装不当、转动件运转时的变形、转动件破损磨耗和转动件附着异物等。不平衡量是转子某平面上不平衡的量值大小。

只考虑各级转子质心相对于回转轴线的偏移产生的不平衡，将各级转子产生的不平衡矢量反映到轴径两平衡平面处的矢量和作为转子整体的的初始不平衡量。如图4所示，平面1、平面2、平面3表示各级转子质心所在平面，平衡平面A、B表示轴径处初始不平衡量所在平面。最终取两平衡平面处初始不平衡量的最大值作为转子整体初始不平衡量大小。

由式(15)求得转子回转轴线，式(16)求得k级转子质心位置矢量向回转轴线投影的长度。

L=PN

(15)

(16)

式中：μk为k级转子质心位置矢量投影到此转子轴线时占轴线总长的比例系数。

第k级转子不平衡矢量为

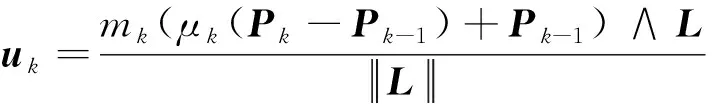
(17)

式中：mk为k级转子质量。

k级转子不平衡矢量反映到平衡平面的初始不平衡量分量、k级转子组件总的初始不平衡量和最终转子整体的初始不平衡量的表达式分别为

(18)

(19)

u=uN

(20)

图4 平衡平面处初始不平衡量Fig.4 Initial unbalance on balance plane

2 转子堆叠多目标优化

采用多目标优化方法将转子不同心误差和初始不平衡量作为优化目标，求解不同心误差和初始不平衡量的最优组合。首先要确定偏差参数dxk、dyk、dzk、γxk、γyk、γzk；各级转子简化为柱形结构[19]，取各级转子高度Hk的上下偏差为±hk，直径φk的上下偏差为±φk，如图5所示，在公差范围内可得

|dxk|≤φk

(21)

|dyk|≤φk

(22)

|dzk|≤hk

(23)

(24)

(25)

(26)

(27)

图5 零件尺寸模型Fig.5 Part size model

当(hk-|dzk|)/0.5φk和(hk-|dyk|)/0.5φk非常小时，式(24)～式(26)改写为

|γxk|≤(hk-|dzk|)/0.5φk

(28)

|γyk|≤(hk-|dzk|)/0.5φk

(29)

|γzk|≤(hk-|dyk|)/0.5φk

(30)

根据式(23)和式(28)，γxk和dzk被限制在图6(a) 所示的阴影有区域内。同理，由式(24) 和式(29)，γyk和dzk被限制在与γxk和dzk相同的阴影有界区域内；由式(22)和式(30)，可以构造出图6(b) 所示的γzk和dyk的约束范围；由式(21)～式(23)， 可以构造出图6(c)所示的dxk和dzk的约束范围。如果首先确定dxk、dzk，剩余参数都会依据其约束范围产生。规定所有零件的公差按照正态分布生成，任何超过[-3σ, +3σ]范围的公差都舍弃。

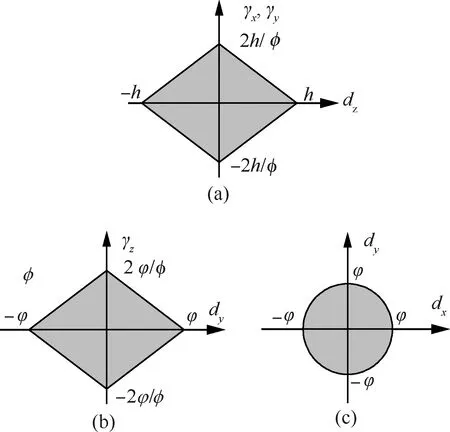
图6 偏差限制范围Fig.6 Deviation limits

根据转子工艺设计要求，确定直径公差2φk和高度公差2hk，则可以确定dxk～N(0,φk/3)、dzk～N(0,hk/3)。dyk、γxk、γxk、γyk、γzk根据其约束范围相继求出，其中所有参数都服从正态分布。

各级转子的安装相位为θk，将θk代入式(11)求得安装相位的旋转算子rk；将γxk、γyk、γzk代入式(12)求得转子上下端面变换的旋转算子Rk；将dxk、dyk、dzk代入式(10)求得坐标系位置矢量Pk；最后将Rk、rk、Pk代入式(8)和式(9)求出各级转子坐标系；通过式(13)和式(14)求出转子不同心误差；由式(18)和式(20)求出转子整体初始不平衡量。

令函数f1为初始不平衡量，f2为不同心误差；则

多目标优化数学模型为

(31)

式中：n为转子安装相位个数。

目前进行优化的算法很多，遗传算法(Genet-ic Algorithm，GA)作为优化算法，通过计算机模拟物种繁衍时，父代遗传基因的重新组合和“优胜劣汰”自然选择机制的联合作用，解决众多复杂工程问题，因此利用遗传算法求解多目标问题在科学研究领域和工程实践领域中得到了广泛应用[20]。采用其中最具代表性非支配排序遗传算法II[21](Non dominated Sorting Genetic Algorithm II, NSGA-II)。其基本思想为：首先，随机产生规模为D的初始种群，非支配排序后通过遗传算法的选择、交叉、变异3个基本操作得到第1代子代种群；其次，从第2代开始，将父代种群与子代种群合并，进行快速非支配排序，同时对每个非支配层中的个体进行拥挤度计算，根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群；最后，通过遗传算法的基本操作产生新的子代种群；依此类推，直到满足程序结束的条件。其算法流程图如图7所示。

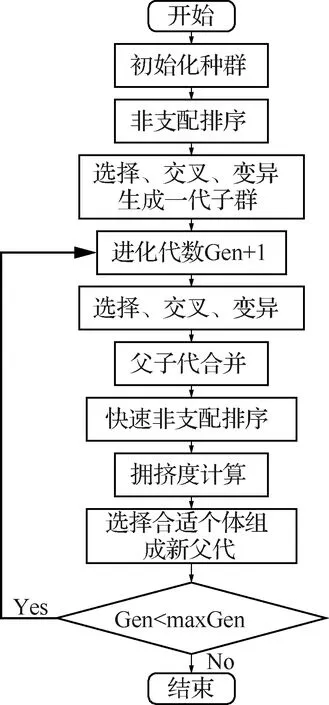
图7 NSGA-Ⅱ算法流程图Fig.7 Algorithm flow chart of NSGA-Ⅱ

3 4级转子36安装相位多目标优化算例

3.1 各级转子参数

根据哈尔滨工业大学设计的HUE-SHS-06[22]模拟转子的直径和高度公差，计算一组转子参数，如表2所示。模拟转子止口配合为过盈配合，螺栓和螺栓孔为间隙配合，只考虑刚体堆叠效果，不考虑螺栓紧固后的受力变形。

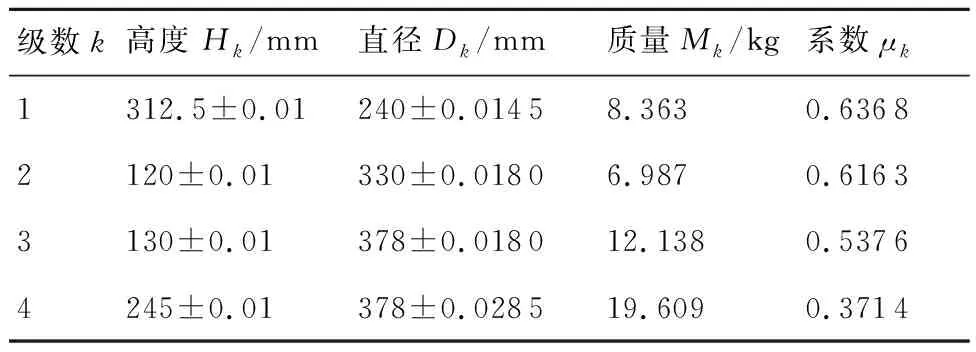
表2 各级转子参数Table 2 Rotor parameters of each stage

令所有参数符合正态分布，将表2中高度和直径参数代入式(21)～式(24)确定平移参数dxk、dzk然后将其代入式(28)～式(30)，可以相继求出旋转参数γxk、γyk、γzk。平移参数精度超过小数点后4位对结果影响可以忽略不计，故取小数点后4位，同理，旋转参数保留3位有效数字，取一组数据如表3和表4所示。

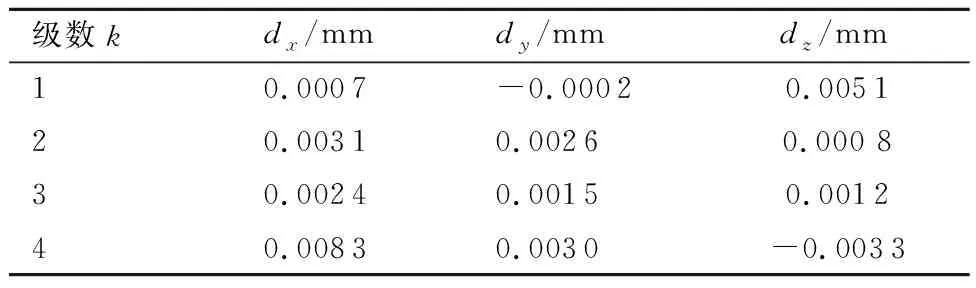
表3 平移参数数据Table 3 Translation parameter data

表4 旋转参数数据Table 4 Rotation parameter data

3.2 优化及分析

装配过程中，各级转子的具体形状尺寸已经确定，转子间的安装相位是唯一可控变量。转子的安装相位由螺栓孔分布决定，螺栓孔均匀分布，参数θk表示安装相位。

转子不同心误差和初始不平衡量双目标优化目标函数及其约束为

(32)

NSGAⅡ算法参数选取如表5所示。优化过程中记录第5、10、20、100次迭代时的Pareto前沿点，取最后一次迭代记录的Pareto前沿点作为最终优化得到的Pareto最优解集，如表6所示。多目标优化Pareto前沿收敛过程如图8所示。取10组随机装配时初始不平衡量、不同心误差和安装相位如表7所示，优化装配和随机装配误差对比如图9所示。

表5 参数选取Table 5 Parameter selection

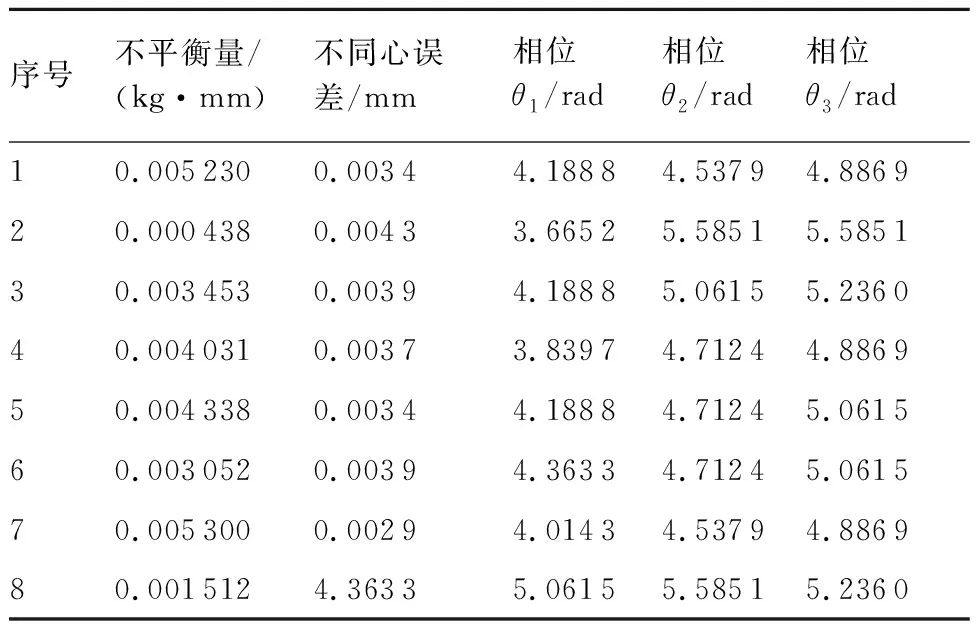
表6 优化结果Table 6 Optimization results

表7 随机装配结果Table 7 Random assembly results

由图8可以观察出，目标函数在优化前20次迭代过程中收敛速度较快，有着较高的收敛效率。在20～100次迭代过程中，随着迭代次数的增加，

目标函数只进行了略微收敛，收敛速度大幅度降低甚至保持不变意味着已经达到最优解集状态，将此时获得的解集作为最终优化装配方案。

由图9可以观察出优化装配结果集中分布在初始不平衡量和不同心误差都比较小的区域，然而随机装配时误差分布范围较广且初始不平衡量和不同心误差较大。由于误差较小的装配方案数目非常少，随机装配时无法保证获得较小误差的装配方案，从而容易造成装配后转子不合格情况。采用优化装配方案可以预测装配后转子误差情况，既提高了装配质量也提高了装配效率。

图9 优化装配与随机装配对比Fig.9 Comparison of optimized assembly and random assembly

根据随机装配方案和优化装配方案数据，取不同心误差和初始不平衡量平均值进行对比，如表8所示。采用优化装配方案时，初始不平衡量降低97.88%，不同心误差降低65.10%，大幅度提高了装配质量。

表8 初始不平衡量、不同心误差降低百分比

优化装配和随机装配不同装配组件数对应的初始不平衡量和不同心误差数据如表9～表12所示。取优化装配和随机装配转子组件不同心误差平均值进行对比，如图10所示；取优化装配和随机装配转子组件初始不平衡量平均值进行对比，如图11所示。

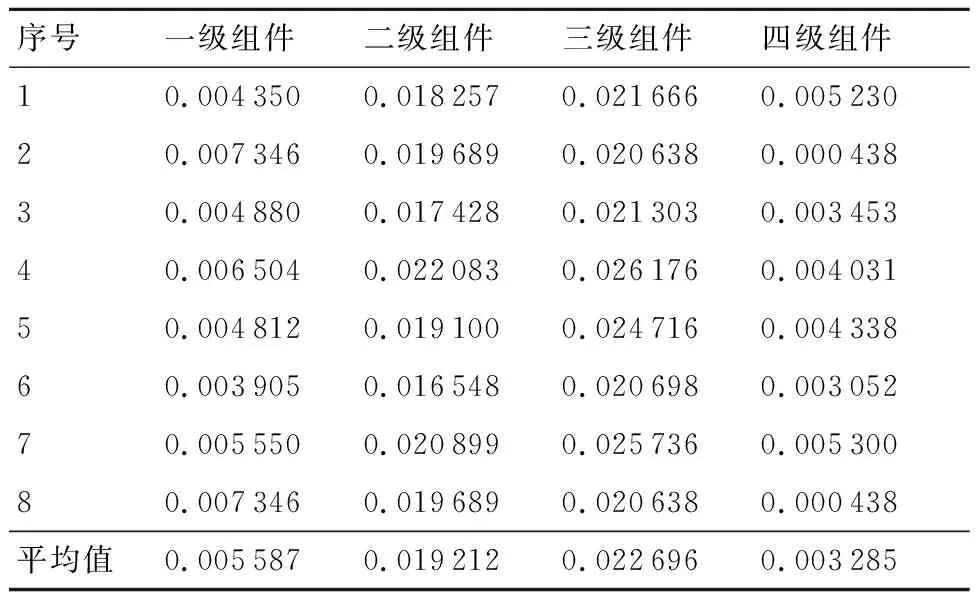
表9 优化装配转子组件初始不平衡量

表10 优化装配转子组件不同心误差

表11 随机装配转子组件初始不平衡量

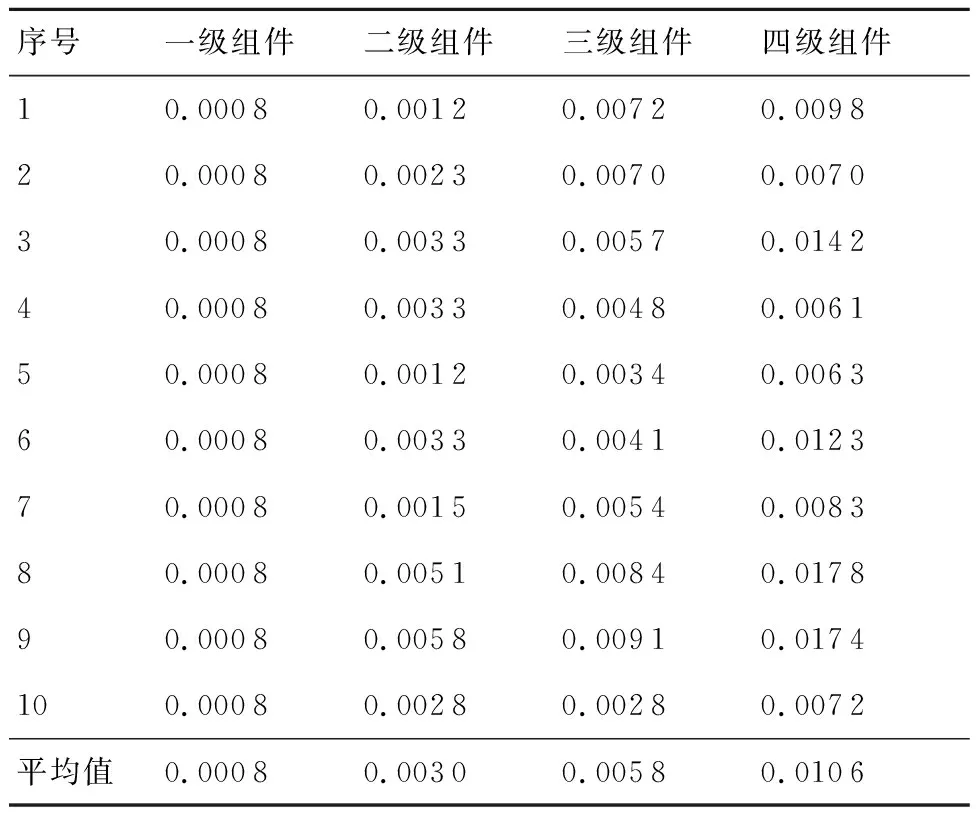
表12 随机装配转子组件不同心误差

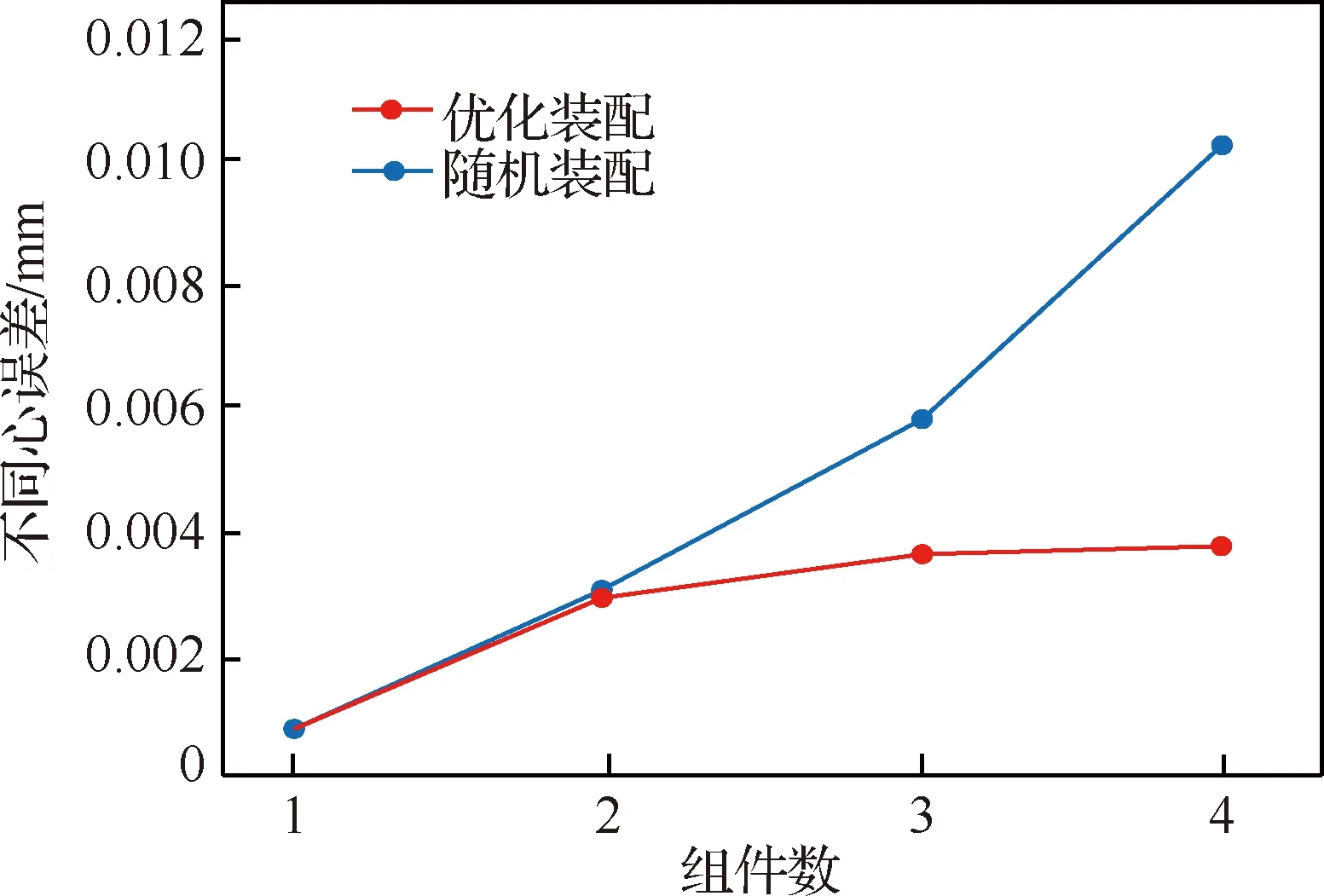
图10 转子组件不同心误差Fig.10 Concentricity of rotor subassembly

由图10和图11显示，随机装配时，不同心误差和初始不平衡量随装配组件数增加而不断增大，且增幅较大。优化装配可以合理安排各级安装相位，虽然随装配组件数目增加不同心误差也不断增大，但是增幅较小，且最终使不同心误差稳定在0.003 7 mm附近。初始不平衡量呈先增大后减小的趋势，同随机装配相比大大降低了初始不平衡量。因此，相对于随机装配，优化装配降低了转子整体的初始不平衡量和不同心误差，提高了转子装配质量。

4 结 论

1) 基于几何代数理论建立航空发动机多级转子堆叠装配误差传递模型模，使模型更加简洁高效，并定义了基于几何代数理论求解不同心误差和转子轴颈处初始不平衡量的方法。

2) 利用遗传算法对不同心误差和初始不平衡量进行多目标优化，确定各级转子的最优安装相位角，得到一组Pareto最优解集作为最优装配方案。优化的装配方案可以预测转子不同心误差和初始不平衡量，与随机装配方案相比初始不平衡量降低97.88%，不同心误差降低64.81%，提高了装配质量。

3) 基于几何代数理论的计算方法应用于转子装配领域，虽然在处理大量旋转问题时计算效率较高，但在计算机编程应用方面，基于几何代数开发的应用程序较少。因此实际应用时，几何代数方法具有一定难度，而基于齐次矩阵变换更加方便和易于实现。在多目标优化方面，优化对象为刚体模型没有考虑止口配合面的受力变形，这方面有待进一步研究。