大数据背景下考虑删失特点的继保设备运行状态评估

张雷，王光华，李金铄，耿宏贤，戴志辉

(1.国网河北省电力有限公司保定供电分公司，河北 保定 071000；2.华北电力大学电气与电子工程学院，河北 保定 071003)

0 引言

继电保护是电力系统的第一道防线，有效利用继电保护运行数据对继保设备状态进行评估，是保持电网安全稳定运行的有效途径[1—2]。

针对继保设备的状态评估，国内外做了大量研究。从继保设备的原理、硬件、配置等方面进行分析、建模、仿真试验，然后对其可靠性进行分析，为设备运行状态评估提供理论依据，也为运维人员提供了提高继保设备可靠性的方法和策略参考[3—4]。例如文献[5]详细介绍了继保设备可靠性研究现状和发展趋势，并指出设备可靠运行是保证电网稳定的重要因素。文献[6]指出设备本身、信息系统和人为因素是保护系统风险的主要来源，并进一步分析了继保设备故障风险对一次系统的影响。文献[7]提出了一种基于变权重模糊综合评价的继保设备状态评价方法，其指标更加完善，但需要足够多的失效样本，而继保设备本身可靠性较高，失效样本数量较少，因此难以满足精度要求。对此，文献[8]在三参数威布尔分布模型的基础上结合灰色模型，在小样本条件下对继保设备进行寿命评估，取得了精度较高的计算结果。文献[9]从扩充样本的角度出发，使用蒙特卡洛法进行抽样，提高了小样本情况下评估结果的稳定性。文献[10]考虑了继保设备缺陷数据的随机截尾特征，基于两参数威布尔分布，采用极大似然估计(maximum likelihood estimation，MLE)实现参数估计，但未考虑区间删失数据的影响。整体上，目前继保设备运行状态评估方法很少计及删失数据的特点，且对包含删失数据的保护运行“大数据”未充分挖掘，造成了信息损失、可靠性评估结果偏颇和分析模型假设过多的问题。围绕电力大数据的分析与利用，国内外学者已进行了大量研究[11—12]。但在大数据背景下，对继保设备的失效数据进行挖掘、分析，从而为判别继保设备状态、评估其运行水平提供可行途径的相关研究，还较少见到。研究基于大数据的继保设备可靠性分析与运行状态评估方法具有重要意义。

文中结合继保设备运行数据特点，首先基于期望-最大化(expectation-maximization，EM)算法对失效模型的参数进行估计，并计算得到设备的可靠性指标；其次，对比各失效期内不同估计方法得到的模型参数精度，验证了方法处理删失数据的有效性；最后，通过算例验证了利用文中方法规划设备检修周期的可行性。

1 大数据背景下失效数据特点分析

长期实践经验表明，设备失效率与累计运行时间之间的函数关系可用浴盆曲线表示。设备的全寿命周期由早期失效期、偶然失效期与老化失效期组成[13]。对于继保设备，出厂前会经过充分的测试以排除隐患，现场安装后，运维人员也会对设备进行严密的调试。因此，可认为继保设备投运后其运行状态便处于偶然失效期。继保设备的失效数据一般是在其投入运行之后收集的现场数据。

受观测条件与监测手段的限制，现场收集到的失效数据可能包含4种类型。

(1)精确数据。继保设备的自检功能日益完善，自检周期非常短，因此自检发现缺陷的时间即可认为是缺陷发生的准确时间。此外，在周期较短的巡视过程中的缺陷发现时间也可认定是缺陷发生时间。这类失效数据称为精确数据，如图1中编号为1、2的失效数据，线段的左端点表示设备的投运时间，右端点表示缺陷发生时间。

图1 原始失效数据Fig.1 Raw failure data

(2)区间删失数据。部分隐蔽性较强的缺陷无法自检查出，无法确定具体发生时间，如专业巡视时发现的“复归按钮脱落”“备用线圈断线”等缺陷，只可推断出发生在本次巡视前、最近一次巡视之后。文中称此类无法确定缺陷发生的确切时间，只能推断时间区间的失效数据为区间删失数据。如图1中编号为3、4的失效数据，线段的左端点表示设备的投运时间，尖括号之间的线段表示缺陷发生时间所在的区间。

(3)右删失数据。在实际工作情况下收集继保设备的失效数据，往往伴随着各种偶然事件。在观察结束之前，有可能会出现样本设备中途退出运行的情形。设备在退出运行之前始终保持正常工作，只能得到设备保持正常工作的时长，此类数据称为右删失数据。如图1中编号为5、6的失效数据，线段的左端点表示设备的投运时间，右端点表示设备退出运行的时间。

(4)随机截尾数据。继保设备的可靠性水平较高，因此直到观察结束，大部分设备仍能保持正常工作。此类直至观察结束仍未出现失效的样本数据称为截尾数据[10]，如图1中编号为7、8、9的失效数据，线段的左端点表示设备的投运时间，右端点表示观察结束的时间，即截尾时间ttr。

因各继保设备的投运时间不同，所以当到达ttr时，各继保设备的运行时间也不尽相同。如果把各样本设备的投运时刻移动到同一计时起点，这些设备的失效数据将表现出随机截尾的特点，见图2。

图2 计时起点对齐后的失效数据Fig.2 Failure data after starting time is aligned

针对继保设备失效数据的上述特点，常用的最小二乘法等算法已无法满足设备失效模型参数估计的需求。文中结合EM算法，利用带有删失特性的失效数据，估计继保设备失效模型的参数。

2 继保设备失效分布模型

失效分布模型能反映设备所处运行阶段及设备的运行状态。采用指数分布模型和威布尔分布模型，通过计算分布模型的参数，估计设备的可靠度R、故障率λ、平均无故障时间tMTBF等指标。其中，指数分布反映偶然失效期的失效特征，常用于拟合具有恒定失效率的设备寿命分布，运行的继保设备多处于该失效期。威布尔分布则可通过不同的形状和尺度参数反映早期失效期(失效率递减)、偶然失效期和损耗失效期(失效率呈加速趋势，如继保设备的老化期)特征，具备较强的灵活性。

2.1 指数分布

指数分布模型[14]的可靠性指标如下。

可靠度函数：

R(t)=e-λt

(1)

式中：t为设备失效时间。

故障概率密度函数：

(2)

失效率：

λ(t)=λ

(3)

平均无故障时间：

tMTBF=1/λ

(4)

2.2 威布尔分布

威布尔分布模型[15—17]可分成三参数和两参数2种形式。两参数模型的函数表达式如下。

可靠度函数：

R(t)=e-(t/η)k

(5)

式中：η>0为尺度参数；k>0为形状参数。

故障概率密度函数：

(6)

失效率：

λ(t)=(k/η)(t/η)k-1

(7)

平均无故障时间：

tMTBF=ηΓ(1+1/k)

(8)

式中：Γ(·)为伽马函数。

3 继保设备运行状态评估

3.1 EM算法

EM算法的基本思想是：当失效数据样本中存在删失数据时，若已知分布模型的参数，则可以结合已知样本数据估计删失数据的数学期望。反之，若已知删失数据的值，则可利用MLE估计分布模型的参数[18]。

EM算法流程简述如下。(1)输入包括删失数据的样本数据；(2)对分布模型的参数赋初值，并设定可接受的最大参数估计误差；(3)执行E步：将上次迭代得到的参数估计结果代入分布模型，估计删失数据的概率分布，并计算删失数据服从此概率分布下对数似然函数的数学期望；(4)执行M步：对参数寻优，使上述期望达到最大，将寻优结果作为本次参数估计的结果并计算估计误差；(5)若参数估计误差小于可接受的最大误差，计算结束，否则返回步骤(3)。

3.2 基于EM算法的指数分布(EM-exp)模型参数估计

指数分布的故障概率密度函数如式(2)所示，其对数似然函数的数学期望为：

(9)

式中：n为样本总数；ti为第i个样本的真实失效时间；z为发生数据删失的样本集；θ，θ′分别为不同分布模型中本次和上次迭代得到的参数；对指数分布，λ′，λ分别为上次和本次估计的故障率参数；Q(·)为似然函数的数学期望；E(·)为ti在服从上次估计的故障率参数下对数似然函数的数学期望。

当Q(θ|θ′)取得极大值时，有：

(10)

根据EM算法的收敛性质，当迭代次数ω→+∞时，λ收敛于定值，即：

λ=λ′ω→+∞

(11)

迭代次数足够多时，将式(10)中的各数学期望项展开，并将式(11)代入式(10)，得：

(12)

采用数值方法求解上述方程即可得到指数分布模型的参数估计值。

3.3 基于EM算法的威布尔分布(EM-wbl)模型参数估计

威布尔分布的故障概率密度函数如式(6)所示。为简化计算，令μ=1/ηk，则式(6)可改写为：

(13)

威布尔分布模型对数似然函数的数学期望为：

(14)

式中：k′,μ′分别为上次迭代所得威布尔分布的形状参数和尺度参数估计结果；k,μ为本次迭代估计的参数。

当Q(θ|θ′)取得极大值时，有：

(15)

(16)

当迭代次数ω→+∞时，参数k,μ将收敛于定值，即：

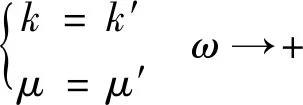
(17)

迭代次数足够多时，将式(15)、式(16)中的各数学期望项展开，并将式(17)代入式(15)、式(16)，得：

(18)

(19)

求解上述隐函数方程组，即可求得威布尔分布参数k,μ的数值解。

传统MLE在处理删失数据时只计及了随机截尾数据，不能处理区间删失数据，会影响继保设备运行状态评估的准确性。而基于EM算法的失效分布模型，在考虑区间删失数据的基础上，可通过对删失数据的还原处理，得到理想的参数估计值并据此计算设备的可靠度、故障率、平均无故障时间等指标，从而实现继保设备运行状态的评估。

4 算例分析

为检验模型的正确性，利用计算机生成带有删失特性的失效数据进行分析。首先，使用蒙特卡罗法生成服从指数分布和威布尔分布的精确失效数据[19—21]，并以此为基础生成带有删失特性的样本集。为模拟区间删失数据，随机选取部分样本进行删失处理。在失效数据的左右两侧分别扩充出删失区间，两侧的删失区间长度服从参数为ζ2,σ2的正态分布，且相互独立。

为模拟右删失数据，在非区间删失样本中随机选取部分样本数据，令其删失时间tc服从(t0,ttr)上的均匀分布，若删失发生在失效之后，则重新分配小于失效时间的tc。其中，t0为投运时间。

为模拟失效数据的随机截尾特征，令计时起点为t0=0，各样本设备的投运时间服从参数为ζ1,σ1的正态分布。若设备的投运时间在计时起点之前，则重新分配大于t0的投运时间。失效时间大于ttr的样本数据即为截尾数据。

4.1 偶然失效区

继保设备工作于偶然失效期时，其失效率基本保持不变。使用计算机生成服从指数分布的失效数据，样本容量为100。生成失效数据时所用参数如表1所示。

表1 参数表(偶然失效期)Table 1 Parameters table (random failure)

分别使用EM-exp模型、EM-wbl模型和传统基于MLE的指数分布模型(MLE-exp)进行参数估计。由于MLE-exp方法不能处理区间删失数据，所以在使用此类数据时，选取缺陷发现时间，即删失区间的右端点作为设备的失效时间。参数估计结果如表2所示，表中p1为使用计算机生成数据时，精确数据在所有非截尾数据中所占比例；p2为区间删失数据所占比例；p3为右删失数据所占比例；tcal为计算耗时。

表2 偶然失效区参数拟合结果Table 2 Parameter titting results of random failures

由表2可得：

(1)删失数据所占比例较小时，与EM-exp模型相比，MLE-exp模型的参数估计耗时最少，且2种模型得到的λ的估计值与真值之间的差距较小。因此，对于失效数据为精确数据的继保设备，宜采用MLE-exp模型进行参数估计。

(2)随着删失数据增多，3种模型得到的参数估计值与真值之间的差距不断增大，此时EM-exp模型准确性最好。因此，对于失效数据中含删失数据的继保设备，宜采用EM-exp模型进行参数估计。

(3)对处于偶然失效期的设备，EM-wbl模型的参数估计结果精度较差。因此，对于具有恒定失效率或定期维护的继保设备，宜采用EM-exp模型进行参数估计。

4.2 损耗失效区

使用计算机生成服从威布尔分布的失效数据，样本容量为100。生成数据时所用参数，如表3所示。

表3 参数表(损耗失效区)Table 3 Parameters table (wearout failure)

指数分布模型不适用于失效率随时间不断变化的情形，所以本节只讨论威布尔分布模型的参数估计精度。分别使用EM-wbl模型和传统的基于MLE的威布尔分布模型(MLE-wbl)进行参数估计，估计结果如表4所示。

表4 损耗失效区参数拟合结果Table 4 Parameter fitting results of wearout failures

由表4可知，当样本数据全为精确数据时，2种方法计算得到的参数k,η以及tMTBF的值均相同。随着删失数据所占比例不断上升，2种方法的估计误差均有所增加，但EM-wbl模型的估计结果更接近准确值，准确度更高。

5 实例分析

5.1 数据预处理

选取某市同一型号的继保设备50台，记设备投运时间为t0，停止观察的时间为截尾时间ttr[22—23]。对于直到观察结束仍未发生缺陷的设备，其累计运行时长tacc为：

tacc=ttr-t0

(20)

对于没有发生故障，但在观察期间退出运行的设备，记其停运时间为tc，其累计运行时长为：

tacc=tc-t0

(21)

对于发生缺陷的设备，若缺陷发现方式为自检，则发现缺陷的时间即为缺陷发生时间tf，设备的失效时间记为：

t=tf-t0

(22)

若发现缺陷的方式为巡视过程，则设备的失效时间区间(t-,t+)的计算方法为：

(23)

式中：T为设备历次巡视时间，取其中距缺陷发现时间最近的一次巡视时间作为设备失效区间的左端点，缺陷发现时间为失效区间的右端点。

整理后的部分失效数据如表5所示，观察期间，50台设备中共有9台发生失效，6台设备的失效时间为精确数据，3台设备的失效时间为区间删失数据，无设备在正常运行情况下中途退出运行。

表5 继保设备失效数据Table 5 Failure data of relay protection equipment

5.2 计算分析

将经预处理的失效数据代入EM-wbl模型中，得到的参数估计值为：

(24)

将参数值代入失效模型中，可得出此型号继保设备的可靠性指标如下。

可靠度：

R(t)=e-(t/60 641)1.717 2

(25)

故障概率密度：

f(t)=1.050 6×10-8t0.717 2e-(t/60 641)1.717 2

(26)

失效率：

λ(t)=1.050 6×10-8t0.717 2

(27)

平均无故障时间：

tMTBF=54 071

(28)

可靠度、故障概率密度、失效率随时间变化的曲线如图3—图5所示。

图3 可靠度曲线Fig.3 Reliability function curve

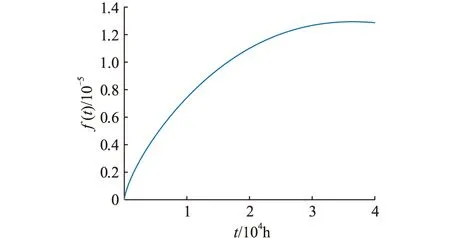
图4 故障概率密度曲线Fig.4 Fault probability density curve

图5 失效率曲线Fig.5 Failure rate curve

如图3所示，当R(t)=0.98时，得到继保设备运行时间为6 250 h，实际运行情况中设备首次失效时间为7 283 h，即通过EM算法得到的参数估计值可以很好的拟合设备可靠度曲线。形状参数k>1，由图4、图5可知，故障概率密度及失效率随运行时间的增加逐渐增大，反映了继保设备处于损耗期的特征。平均无故障时间tMTBF可用于检修周期制定，通常情况下状态检修周期Tm=0.1tMTBF，即建议状态检修周期为5 407 h。

综上可知，当存在删失数据时，采用EM-wbl得到的参数估计值可更精确地拟合设备实际的失效情况，再根据继保设备可靠度、失效率、故障概率密度等指标随时间变化的曲线预判其寿命分布，达到评价继保设备运行水平，预测设备运行年限的目的。

此外，上述分析的失效数据来自同类型设备，因此得出的结论适用于该类型设备。但所提模型对不同型号设备具有普适性。

6 结语

首先分析了继保设备失效数据的特点，总结了现场收集到的失效数据类型：精确数据、区间删失数据、右删失数据和随机截尾数据。然后在失效数据样本包含删失数据的情况下，对比分析了偶然失效期和老化失效期内不同估计方法得到的模型参数精度。证明在偶然失效期内，EM-exp模型得到的参数估计精度更高；在老化失效期内，EM-wbl模型能以更高的精度拟合继保设备的失效特性曲线。

最后通过对某型号设备数据处理，结合失效分布模型，分析了该继保设备可靠度、失效率、故障概率密度等可靠性指标的时变特征。利用设备可靠度曲线，可提前判断设备可靠度，降低到阀值所需的时间，并及时发出告警提醒工作人员加强巡视。利用失效率曲线，可得设备的故障风险随时间变化的规律，用于安排检修计划。利用故障概率密度曲线，可计算设备的平均无故障时间，为合理安排服役年限提供参考。下一步将针对不同类型删失数据，对比研究不同算法的参数估计精度。