基于小波模型的同步调相机转子故障诊断

张玉良，蔚超，林元棣，马宏忠，陈浈斐，蒋梦瑶

(1.河海大学能源与电气学院，江苏 南京 211100；2.国网江苏省电力有限公司电力科学研究院，江苏 南京 211103)

0 引言

随着新能源的并网与特高压直流输电的发展，电网对无功调节的要求也逐步提高，随着电压等级的提高，系统整体的稳定性和安全性问题也日益严重。调相机是一种大型无功调节设备，其增加无功和吸收无功的能力都较强，在电力系统中可以加强电压的动态调节能力[1—4]。例如在特高压变电站，调相机可以有效避免电力系统电压突然提高，尤其是在电网侧，调相机可以快速吸收大量由于换相失败而产生的无功功率，同时又能大量增加无功，加快故障后系统无功的恢复[5]。因此，大型调相机是电力系统中调节无功的重要装置。

对于大型调相机，其励磁绕组匝间短路故障在初期并不严重，大多数情况下仅是在绕组间有微小的接触，然而这一情况是不平稳的，从某种程度来看，会令调相机的励磁绕组电流越来越大，无功功率不断下降，使轴承振动幅度不断加大。通常情况下，励磁绕组匝间短路初期，调相机可以正常运行，然而若工作条件不佳，比如三相负荷不对称，那么调相机仍可以持续工作，但在调相机中出现的负序旋转磁场会导致发生短路的转子绕组产生倍频电动势形成回路，从而使短路环电流越来越大，短路点温度越来越高，相邻绕组绝缘老化也越来越快，最终这一情况不断反复[6—7]。因此没有被及时发现的一部分轻微故障如果继续长期运行最终会导致严重故障。调相机内部一旦出现较为严重的故障甚至宕机，不仅需要投入大量的人力、物力来修整这些设备，而且整个电力系统的稳定性和安全性都会受到影响，造成巨大的经济损失和社会影响。

近几年调相机才被重新装机运行，针对转子绕组匝间短路的相关鉴别方法较少。但调相机本质上就是没有原动机和机械负载的同步电机，因此可以根据当前对于大型汽轮发电机等同步电机的研究对调相机进行类比分析[8—9]。文中通过分析同步电机数学模型，推导得到励磁电流与转子绕组匝数之间的对应关系，并利用小波包分析与径向基函数(radial basis function，RBF)神经网络相结合的形式对匝间短路故障进行仿真诊断分析，为其他相关机组的实验分析提供了数学仿真模型的参考。

1 调相机励磁电流模型

若调相机转子绕组在正常运行中发生了匝间短路故障，那么匝间短路就相当于励磁绕组的有效匝数降低，而气隙合成磁通的原本条件没有发生改变，所以只能是励磁电流升高[10—14]，同时短路匝中也相当于增加了一个短路回路(短路环)。对励磁电流的计算思路如下：将调相机转子绕组匝间短路后的输出当作没有发生短路的正常输出值，代入反向算出励磁电流，则计算值与实际测量值之间的差值就可以用来识别是否发生转子绕组匝间短路故障，并判断出其故障程度。

对于dq坐标系来说，结合派克表达式对其逆向推理，能够得出同步电机的派克表达式。设电机运行在对称稳态下，δ为功角，则边界条件为：

(1)

式中：ild为直轴阻尼绕组电流；ilq为交轴阻尼绕组电流；io为零序电流；ia，ib，ic为三相电流；ud为直轴电压；uq为交轴电压；U为端电压；ψd为直轴磁链；ψq为交轴磁链。

将上述边界条件代入派克方程可得：

(2)

(3)

式中：id为直轴电流；iq为交轴电流；xd为直轴同步电抗；xq为交轴同步电抗；E为电动势；r为定子电阻。同步电机中定子电阻r值很小，因此可以通过忽略r简化式(3)，结果如下：

(4)

将式(4)代入同步电机派克方程可以得到有功和无功输出如下：

(5)

因为是隐极同步电机，所以xd=xq，代入上式可得：

(6)

同步电机的空载电动势为：

(7)

式中：xad为直轴电枢反应电抗；Ifd为励磁电流；Lad为直轴同步电感；Mafd为定子绕组与励磁绕组互感系数；τ为调相机的极距；l为定子铁芯的有效长度；p为调相机的极对数；ωfd为调相机转子绕组的匝数；as为调相机定子绕组的支路数；afd为励磁绕组支路数量；koδfdl为绕组系数；koδl为定子绕组的基波绕组系数；ω为绕组匝数；λdll为气隙磁导系数。

对于同步电机来说，未出现匝间短路情况下，其励磁电流为：

(8)

式中：Lδ为定子自感基值；kifd为定子电流基值与转子电流基值比；S为视在功率；Q为无功功率。

如果转子绕组出现匝间短路问题，用Δn来代表其短路匝数，那么出现故障后的匝数为：

ω′fd=ωfd-Δn

(9)

将其代入式(8)，则出现故障后的励磁电流：

(10)

假设调相机转子绕组发生匝间短路故障后其有功和无功输出都保持不变，则将式(8)和式(10)相比可得：

(11)

根据式(11)可知，发电机转子绕组发生匝间短路故障前后励磁电流与匝数有着对应关系，且与发电机的有功和无功输出无关，因此可以将发电机励磁电流认作是否短路及短路程度的判别参数。

2 调相机绕组匝间短路仿真

通过上述分析能够得出，结合励磁电流的改变，能够判断出转子绕组是否出现匝间短路等情况，因此利用仿真得到发电机在不同匝间短路程度以及正常情况下的励磁电流波形，有利于下一步利用神经网络来诊断故障。应用Matlab建立转子绕组匝间短路问题模型，电机部分参数有：调相机定子绕组的电阻值r=2.906 9 Ω；励磁绕组的电阻值Rfd=0.590 13 Ω，Rkd=11.900 Ω，Rkq=20.081 Ω；励磁电压Ufd=24 V；绕组的匝数ω=377。

根据调相机基本参数构造电感系数矩阵和电阻矩阵，并在dq坐标系下建立电压过程微分方程，利用Matlab中可变阶数的多步算法ode113(adams)求解微分方程，得到励磁电流的变化曲线，对调相机启动运行以及匝间短路程度分别为20%和50%时进行仿真，励磁电流变化情况如图1—图3所示。

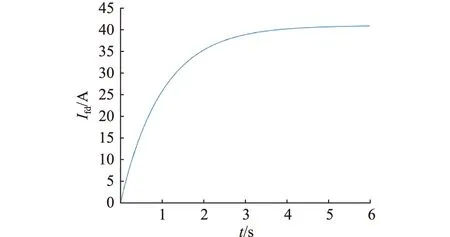
图1 启动运行中励磁电流Fig.1 Excitation current in start-up operation

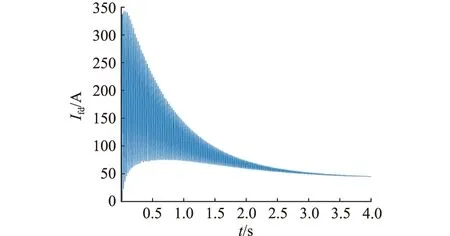
图2 绕组匝间短路程度20%时励磁电流Fig.2 The winding turns short the excitation current by 20%

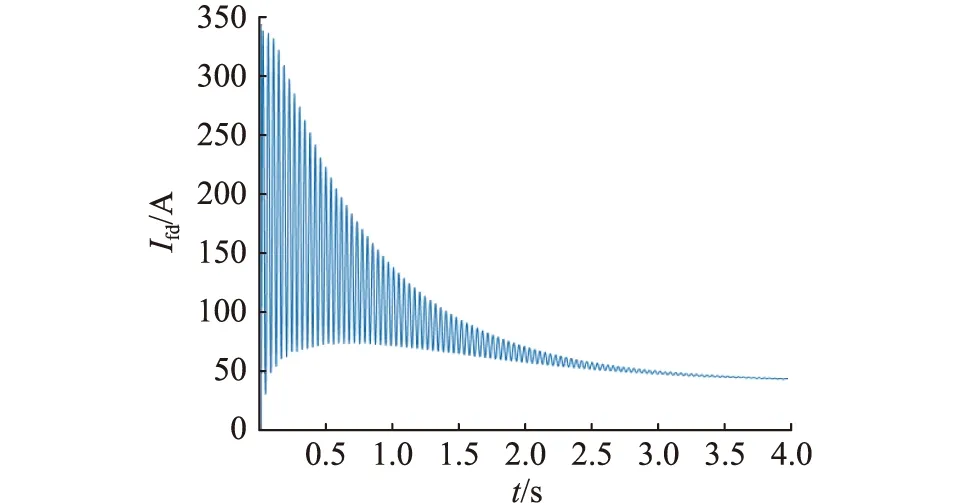
图3 绕组匝间短路程度50%时励磁电流Fig.3 The winding turns short the excitation current by 50%

3 小波模型提取故障特征信息

文中采用小波分析与基础神经网络模型相结合的方式对数据进行特征提取，根据搜集到的文献资料可知，目前将小波分析与神经网络相结合主要有2种方法：(1)先利用小波分析对待处理信号进行第一步处理，再将结果送入神经网络进行分析；(2)用小波元替代神经网络中的神经元，同时保持神经网络本身的结构不变，从而将二者相结合，大大提高计算效率，而且这种方式具有不同的分辨率，即在数据量大的地方使用高分辨率，在数据量小的地方使用低分辨率，同时对数据进行小波分析，并适时地调整各种因子来提高分类效果[15—17]。文中设计的小波模型采用第二种方法。

基于多层感知机的传播过程，将该小波模型分为3层：输入层、隐藏层和输出层。3个前馈网络集中在一层隐藏层中可以使得该网络模型以任意精度无限趋于任意函数(文中取非线性映射)。图4为三层小波模型的结构示意。

图4 小波模型结构示意Fig.4 Schematic diagram of wavelet model structure

通过多次建模对比，Morlet小波函数是能够最快实现模型训练完成的基函数，因此选其作为模型隐藏层中的激励函数，即：

(12)

(13)

式中：a为Morlet小波函数的伸缩因子；b为Morlet小波函数的平移因子。

假设第i个节点对应的第m个写入样本为xim，OIim为输入层(即I层)的第i个节点对第m个写入样本的输出，OJjm为隐藏层(即J层)第j个节点的输出，OKkm为输出层(即K层)第k个节点的输出，则I层第i个节点的输出值为：

OIim=xim

(14)

J层第j个节点的输出值为：

(15)

式中：NI为输入层节点数量；aj为小波函数第j个节点的伸缩因子；bj为小波函数第j个节点的平移因子；ωij为OIim对应的权值。

K层第k个节点的输出值为：

(16)

式中：NJ为隐藏层节点数量；ωjk为OJjm对应的权值。

则能量函数，即误差为：

(17)

式中：YKkm为相应样本的实际输出；NK为输出层节点数量；M为对应样本的容量。

将上述小波模型计算所得各能量值进行归一化处理。如果输入神经网络的特征值太大有时会导致网络饱和，所以需要将根据调相机励磁电流信号计算所得的各能量值归一化，过程如下：

(18)

(19)

式中：Eij为各频率段的能量值；Esum为各频率段的总能量；E′ij即为归一化的能量值。

归一化后，利用能量值形成特征向量：

T′=(E′i1,E′i2,…,E′in)

(20)

利用上述小波模型对调相机转子绕组发生不同短路程度故障时电机的励磁电流进行分析，得到各频率段的能量值和总能量值，并进行归一化处理，最终构成故障特征的样本数据库，送入RBF神经网络进行故障诊断。

4 RBF神经网络故障诊断

RBF神经网络是三层前馈神经网络之一，具有整体优化的优点，且其逼近效果也较好，被大量运用于模式分类等。RBF神经网络主要包括输入层，隐藏层和输出层。但不同于常规多层感知器，其不同层有着各不相同的功能，尤其隐藏层是非线性的，RBF能够将输入向量空间向隐藏层空间进行转变，这样线性不可分问题便可向线性可分问题进行转变，输出层则是线性的。而RBF神经网络主要特点就是隐藏层神经元应用欧氏距离，将其当成是基函数，且其激活函数使用的是高斯函数。

RBF神经网络的隐藏层可写为φi(‖x-ci‖)，表示隐藏层中i个神经元相对应的激活函数，其中x为RBF神经网络中样本数据的输入向量，ci=[ci1ci2…cin]T，且ci∈Rn，为隐藏层中的神经元向量。实际应用中RBF的输出节点能够使用很多种函数，文中使用线性函数。由此可总结出RBF神经网络的第j个输出表达式如下：

(21)

式中：ω′ij为输出层、隐藏层间的权值；dj为输出层中不同神经元的阀值；i为隐藏层不同神经元的编码；j为输出层不同神经编码。

BRF神经网络不可能出现局部极小值，其函数逼近效果要好一些，可以通过输入数据的数量或结束运算的阀值条件等命令的选择使得网络以任意精度对复杂函数进行逼近。

小波模型具有更高的分辨率和精确度，可以对故障信号的高频部分再次进行多层分解，对于提取信号特征信息作用很大。RBF神经网络在训练速率、自适应性等方面优势较大，能够较好地完成电机的故障诊断任务。因此文中将上述两者相结合，通过小波模型对调相机故障励磁电流信号提取特征值，将结果向RBF神经网络传送，从而诊断出故障，其整体流程如图5所示。

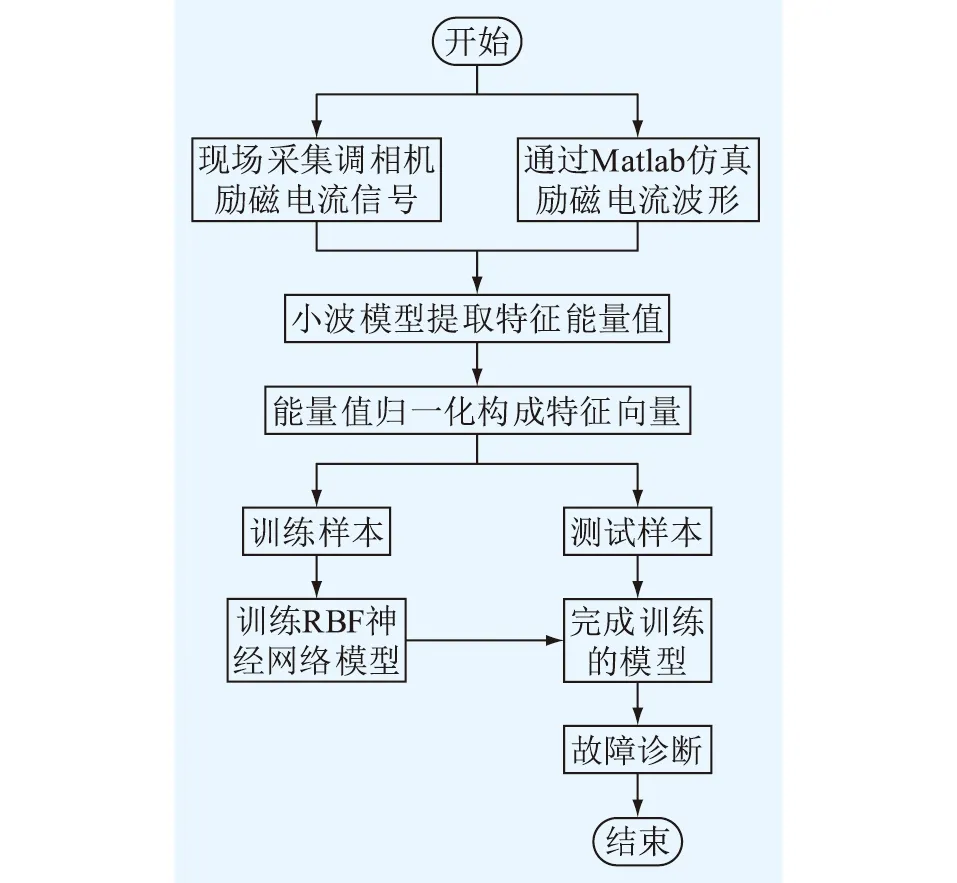
图5 调相机转子故障诊断流程Fig.5 Flow chart of rotor fault diagnosis for synchronous condenser

具体的故障诊断过程如下：

(1)通过Matlab对调相机转子绕组发生匝间短路时的励磁电流进行仿真，并利用小波模型分析进行特征提取，作为神经网络的输入向量。文中利用小波模型提取了150组样本特征用于模型训练，向RBF神经网络输入样本数据进行计算对比分析。

(2)建立RBF神经网络模型[18—19]，输入层节点有4个，输出层节点有5个。

(3)向RBF神经网络送入训练样本进行模型训练，网络的收敛如图6所示。

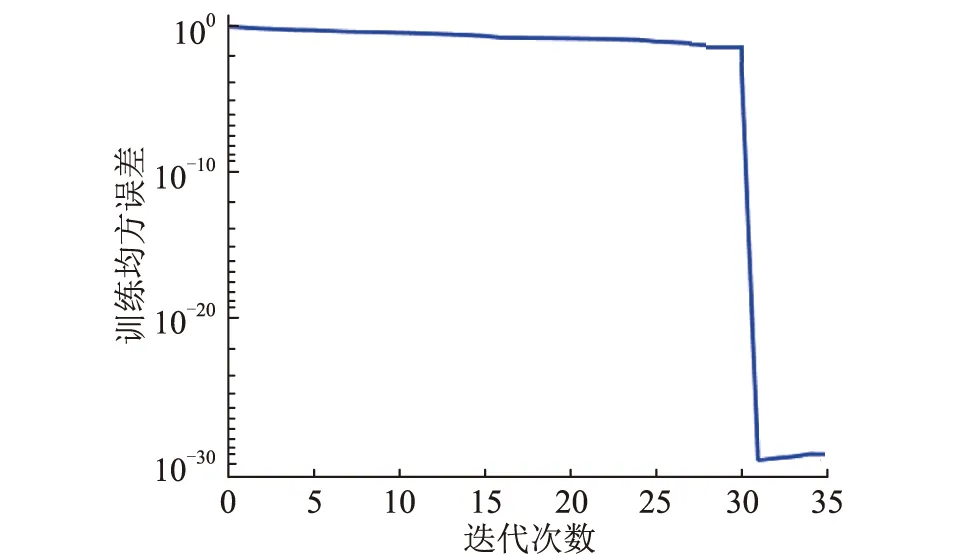
图6 RBF神经网络收敛情况Fig.6 Convergence of RBF neural networks

经过计算发现，当RBF神经网络模型迭代30次时，训练均方误差已经达到2.405 41×10-30，收敛速度较快。

(4)完成网络模型训练后，额外提取50组样本特征用于模型测试，将测试样本送入RBF神经网络，测试该模型对转子绕组匝间短路的故障能否精确判别，模型输出结果如表1所示。

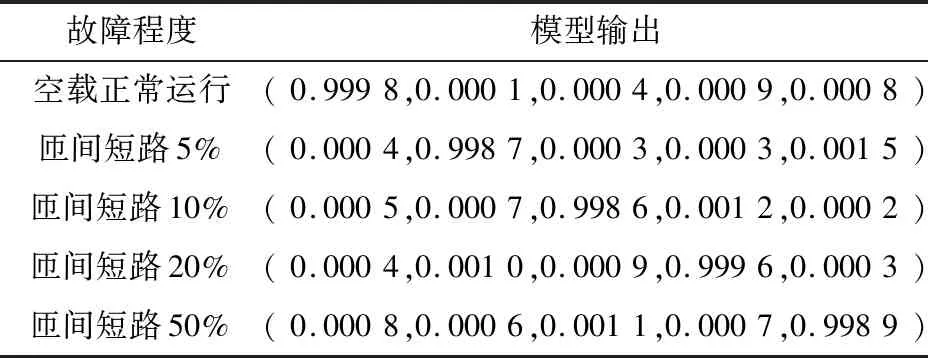
表1 RBF神经网络模型输出Table 1 RBF neural network model output

由表1可以发现，RBF神经网络的输出结果已经非常逼近期望输出(各类型对应输出结果为1)，且收敛速度较快，展现了RBF神经网络诊断电机故障的优势。

5 结语

文中建立了调相机励磁电流的数学模型，在dq坐标系下利用派克方程推导得到转子绕组匝间短路与励磁电流之间的关系，并通过Matlab求解同步电机微分方程对不同故障程度下的调相机励磁电流进行仿真。再利用小波模型对励磁电流信号进行特征提取，然后输入RBF神经网络进行故障诊断，验证了基于小波模型的调相机转子绕组匝间短路故障诊断方法的快速收敛性及高精度。

本文得到国网江苏省电力有限公司科技项目(J2019114)资助，谨此致谢！