基于卡口数据的城市道路交通空间相关性分析
宋大创,马晓旦,夏晓梅,孙明洁
(上海理工大学 管理学院,上海 200093)
0 引言
在城市道路系统中,某路段的交通状态(如速度、流量)会受到其周围路段交通状态变化的影响。道路之间的这种交通依赖关系,通常被称为道路交通空间相关性。对城市道路交通空间相关性进行探讨,有助于理解城市道路系统的内部交互作用方式,并为交通插值和预测提供基础。
现有研究及应用通常假定一定空间或拓扑距离内的道路具有交通空间相关性。例如:文献[1]认为,一定距离内的道路具有空间相关性;文献[2]中将一定时间内可达的路段视为交通相关道路;文献[3]则假定一定拓扑距离内的道路具有空间相关性,并将其应用于交通预测;文献[4]在交通数据插值时,使用拓扑距离来定义道路,并利用统计学中的相关系数法,确定研究区域内路段的互相联系;文献[5]为了获取交通联系的所有空间和时间相关性,采用了皮尔逊相关系数分析。结果表明,各路段的交通流量呈正相关关系,且不遵循任何距离模式。然而这些应用于快速路或高速公路的方法,在城市道路中并不太适用。众多研究表明少部分城市道路承担了绝大部分的交通流。交通流的传播扩散也具有各向异性,上游路段的车辆不会均匀扩散到所有下游路段,而是会比较集中在某个或多个特定方向上,使得道路之间的交通相关性具有空间异质性[6-7]。因此在度量城市道路之间的相关性时,考虑其空间异质性是非常必要的。
本文从卡口数据中提取出研究路段的交通流时间序列,进行去时间趋势分析,利用统计学中的相关系数法得到网络权重矩阵,同时提取研究区域内每辆车行驶轨迹,形成流量转移矩阵,再通过ochiai 系数(余弦相似性度量的一种形式),得到流量转移权重矩阵。结合这两个矩阵,重新度量不同路段之间交通空间相关性,进行短时交通流预测及效果比较,验证方法的可行性和有效性。
1 城市道路交通空间相关性分析方法
从道路网络上不同时间、不同地点观测到的交通流,包括时间和空间的相关性。然而从历史数据集提取的时间相关性,通常超过空间相关性,因为其比空间相关性更强烈[8]。因此,为了深入探讨空间相关性,有必要去除交通流数据中时间趋势的影响。
本文选取去除网络空间平均趋势的方法,即对每个检测周期,计算待考察网络中各节点流量的平均值。由于不同路段设计的通行能力不同,其流量趋势也存在一定的比例关系。每个路段检测到的流量,都按比例减去网络平均流量,形成去趋势后的路段流量时间序列。
(1)去时间趋势分析
对于记录的各路段流量时间序列qi∗,i =1,...,N,其空间平均趋势计算方法如式(1)所示。
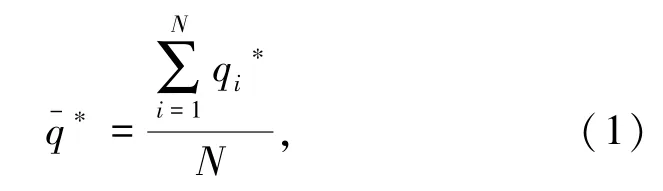
其中:N为研究区域内的总路段;为研究区域内空间平均趋势;qi∗为研究区域内各路段的流量时间序列。
设Ri为路段i在Nτ个采样周期内流量总和与网络所有节点在Nτ个采样周期内流量总和之比,用于反映不同路段间流量日趋势的比例。如式(2)所示。

其中:qik为路段i在第k个采样周期的流量,Ri为不同路段间流量日趋势比例。
从各路段原始记录流量序列中,按比例减去网络空间平均趋势,得到去趋势后的流量时间序列,如式(3)所示。

其中:为去时间趋势后的流量时间序列。
(2)根据去趋势后的流量时间序列,通过式(4),得到路段i与路段j之间的网络权重矩阵。

其中:cov(i,j)为的协方差,为的方差。
(3)提取每辆车的行驶轨迹,并建立流量转移矩阵后,通过Ochiai 系数得到流量转移权重矩阵。
①根据卡口设备收集到的车辆记录,提取每辆车的行驶轨迹,定义如式(5)所示。
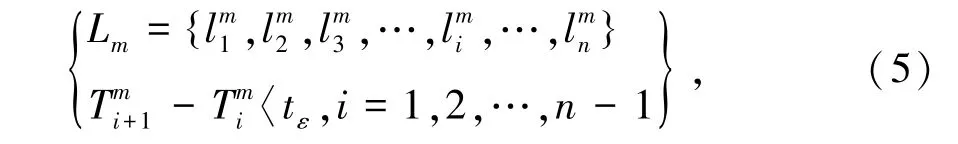
其中:Lm为第m连续通过的n个路段的路径;为第m辆车通过第i个路段;为第m辆车通过第i个路段的时间;tε为时间阈值10 min。
②流量转移矩阵表示为VTM∈RN×N。其中,N为研究区域考虑的交叉口的总进口道数。流量转移矩阵构建过程如下:
Step 1提取每辆车c(1 ≤c≤m)在研究区域内的起点和终点;
Step 2提取每辆车经过的路段位置i(1 ≤i≤n-1),j(2 ≤j≤n);
Step 3。
上述VTM矩阵仅代表每个进口道流出的交通量,对于大多数城市道路而言,既有流出量也有流入量。因此,本文将流出量和流入量的总量作为两个进口道间的总转移量。最终的流量转移矩阵可以结合其转置矩阵定义,如式(6)所示:

VTM∗矩阵中的元素值越大,说明车辆轨迹共享上下游的次数越多,其之间具有较强的交通空间相关性。
③通过Ochiai 系数(余弦相似性度量的一种形式)将交通流量转移矩阵VTM∗转为i与j路段之间的流量转移权重矩阵Q(i,j),如式(7)所示。
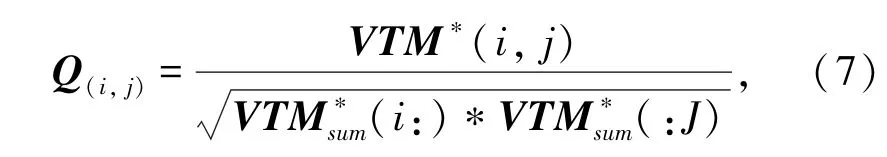
④为了识别与目标路段空间相关性最高的几个路段,定义路段i与j之间的距离如式(8)所示。
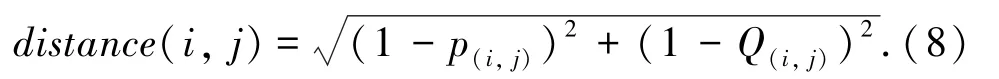
距离越小,说明路段i与j空间相关性越高。
2 实例分析
2.1 数据说明
本文实验以某市城市道路卡口系统采集到的交通流数据为例,分析了不同路段之间空间相关性。选取9 个交叉口、36 个进口道、采集10 个工作日的交通数据。其中,前9 个工作日的数据为训练数据,第10 个工作日的数据为预测数据。采集时间间隔为5 min。其空间关系如图1 所示。
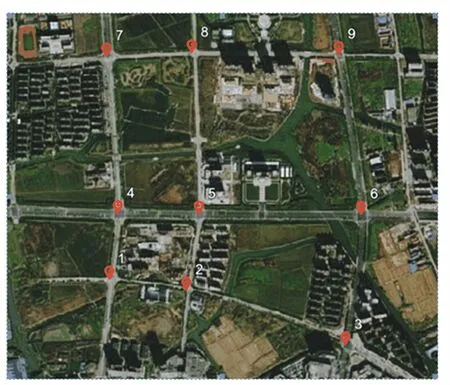
图1 卡口检测器位置Fig.1 Position of bayonet detector
2.2 预测结果比较
LSTM(Long Short Term Memory Network)长短时记忆网络,是一种改进之后的循环神经网络,在时间序列预测问题上有着广泛的应用。
本文采用LSTM 模型进行多维单步预测,度量空间相关性的准确性。具体分为以下3 种情况:
(1)仅考虑研究路段与其对应的上游多维时空的交通流数据;
(2)考虑研究路段与其对应的上下游的多维时空交通流数据组合。
(3)根据本文的空间相关性度量方法,提取4个与研究路段空间相关性最高的路段,组成多维时空交通流数据组合。
本文假设某时段的交通流数据仅与其紧邻的前3 个时段的数据具有较强的相关关系。采用LSTM预测模型进行短时交通流预测,选取MAE(平均绝对误差)、MAPE(平均绝对百分比误差)、RMSE(均方根误差)进行预测误差结果对比。以进口道A 为例,3 种情况预测比较结果见表1。

表1 不同情况下的预测结果Tab.1 Forecasting results under different conditions
从实验结果可见,只考虑上游路段的情况下(情况1),预测精度最低;只考虑上下游路段(情况2)的预测精度其次;在考虑了空间异质性(情况3)的情况下,充分提取与研究对象道路交通空间相关性最高的路段,则预测精度最高。验证了本文提出方法的有效性,为今后预测路网的交通流状态提供依据。
2.3 空间相关性分析
根据本文提出的空间相关性分析方法,提取与路段A相关性最高的前4 个路段,其空间分布如图2所示。从图中可以看出,这些关联的路段可以分为两类:直接相连的路段(路段a、b)和非直接相连的路段(路段c、d)。对于前者,是目标路段A的交通量流入或流出方向,这些地点的交通状况对目标路段A有直接影响;对于后者,虽然其之间的车辆过渡很少,但其交通量变化趋势具有相似性。因此,本文提出的空间相关性分析方法既能反映车流量转移关系,又能从统计角度捕捉交通流在空间上相似的趋势。
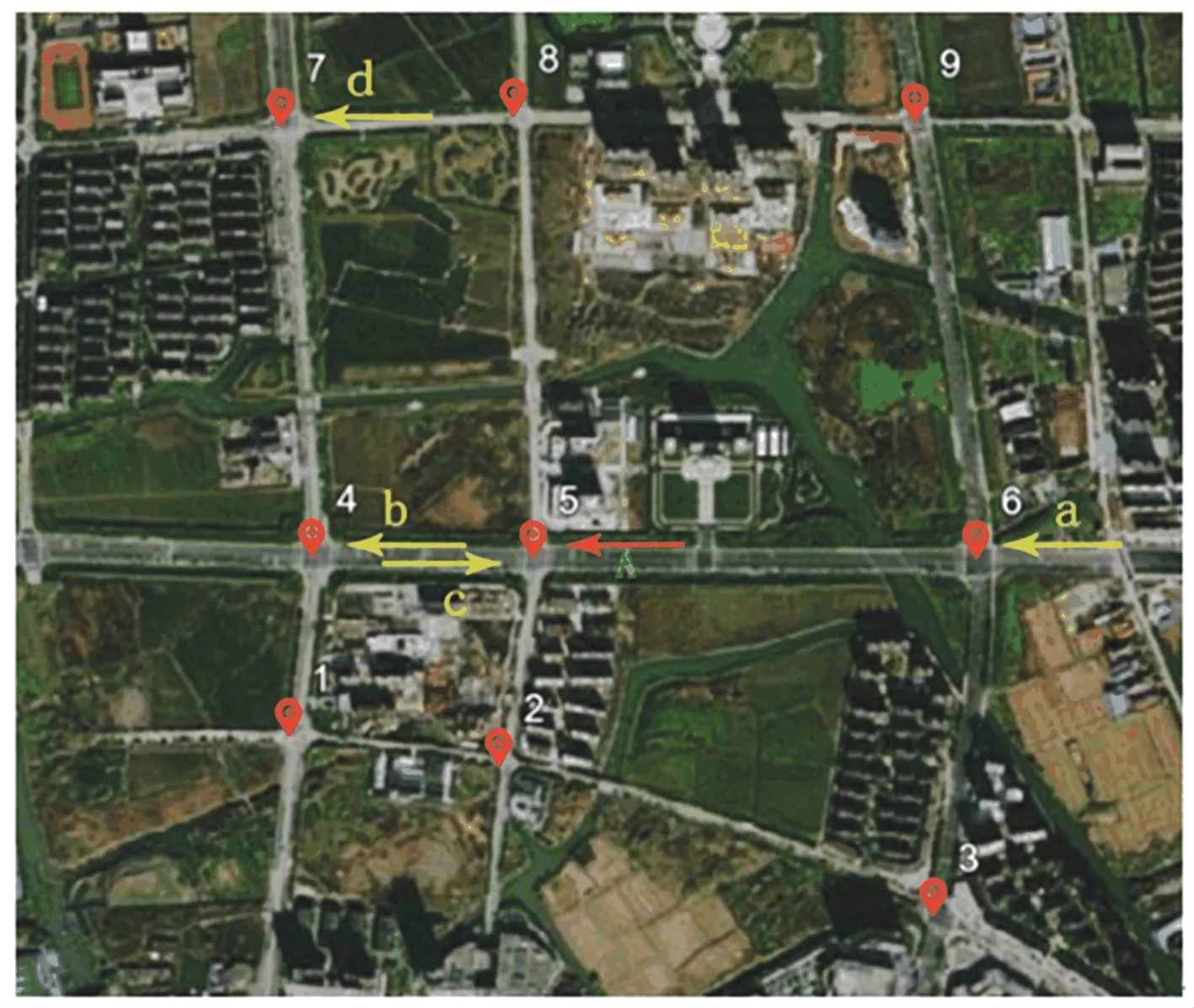
图2 与进口道A 相关性最高的前四个路段空间分布Fig.2 Spatial distribution of the first four sections with the highest correlation with inlet road A
3 结束语
机动车的出行不但构成了整个路网的交通分布模式,也是道路之间产生交互影响和交互作用的根本原因。本文结合车辆轨迹得到的流量转移权重矩阵和不同卡口数据量化的网络权重矩阵,构造一个新的网络权重矩阵,较准确地描述了城市道路之间的交通空间相关性,为以后能更好更快的预测路网上的交通流状态提供依据。

