遗传算法优化的支持向量机回归计算老龄化人口方法
张馨予,孙宏宇,逯 洋,郭天岚
(吉林师范大学 计算机学院,吉林 四平 136000)
0 引言
随着科学技术的迅速发展,人民生活水平不断提高,人的寿命正不断延长。据国家统计局发布,中国平均预期寿命已由2005 年的72.95 岁增长到2015 年的76.34 岁。与此同时,中国人口出生率由2001 年的13.38%下降到2019 年的10.48%(如图1)。为尽可能减小老龄化社会带来的负面影响,有必要对老龄化人口进行精准预测。本文利用支持向量回归模型(SVR)进行预测,但由于SVR 的预测能力在很大程度上受到初始参数的影响,参数不同可能会导致欠拟合或过拟合的问题。因此,本文使用具有强大全局搜索能力的遗传算法(GA),对SVR的初始参数进行优化,进一步提高其预测准确率。

图1 2001-2019 年平均预期寿命与出生率Fig.1 Life expectancy and birth rate from 2001 to 2019
1 SVR 原理
支持向量机回归,是由支持向量机模型[1]衍生出来的,其目的是发现非线性回归问题中存在的自变量与因变量之间的关系。通过引入非线性映射函数,将低维空间中具有非线性回归关系的数据集映射到高维空间,然后对其进行线性回归关系变换[2]。其数学表示为:
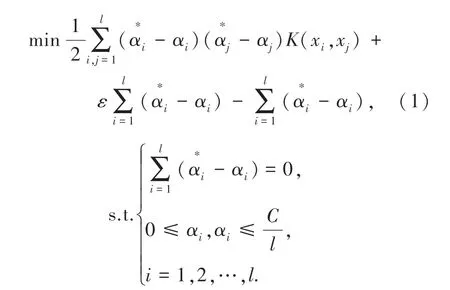
其中,训练样本为xi,i =1,2,3,4,…,l;K为核函数;C为惩罚函数,C越大表示对误差ε的惩罚越大。
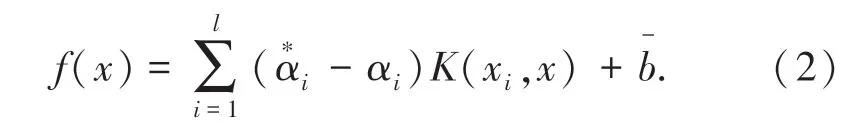
2 GA-SVR 模型构建
遗传算法(GA)[3]在1975 年由Holland 等人提出,随后Goldberg[4]与DeJong[5]等人将遗传算法归纳为一种模拟自然界生物遗传和进化的随机搜索智能算法,适用于复杂系统的优化问题。与其它传统的搜索算法不同,GA 算法并不是基于单一评估函数的较高次统计或梯度产生的确定性的实验解序列,而是通过模拟生物的进化过程来搜索最优解。GA 算法适用于解决大部分优化问题,随着算法的迅速发展,其影响范围也越来越大。
本文引入遗传算法,解决SVR 的预测能力依赖于初始参数的问题,利用遗传算法的全局搜索能力,搜索支持向量机的最优参数,其中包括:惩罚函数(C)、gamma(g)。工作流程如图2 所示。

图2 GA 优化SVR 初始参数流程图Fig.2 GA optimization flow chart of SVR initial parameters
实现步骤如下:
(1)设置遗传算法相关参数。
(2)将支持向量机回归模型的惩罚函数(C)与gamma(g)进行二进制编码,产生遗传算法初始种群。
(3)将随机产生的数据输入到支持向量机回归模型中,进行交叉验证得到平均准确率,作为遗传算法的目标函数。
(4)进行交叉、变异、选择等操作。
(5)判断是否满足终止条件,满足则输出结果,否则转到步骤(4)。
(6)将最终结果输入到向量机回归模型中,从而得到参数优化后的向量机回归模型,用于进行老龄化人口预测。
3 实验及结果分析
3.1 数据集
研究人口老龄化问题需要相关指标进行实证分析,本文最终选取了7 个与人口老龄化相关的因素指标:15~64 岁人口数- x1(万人)、出生率-x2(%)、死亡率- x3(%)、人口自然增长率-x4(%)、居民消费水平- x5(元)、人均GDP-x6(元),离退人员参加养老保险人数-x7(万人),见表1。
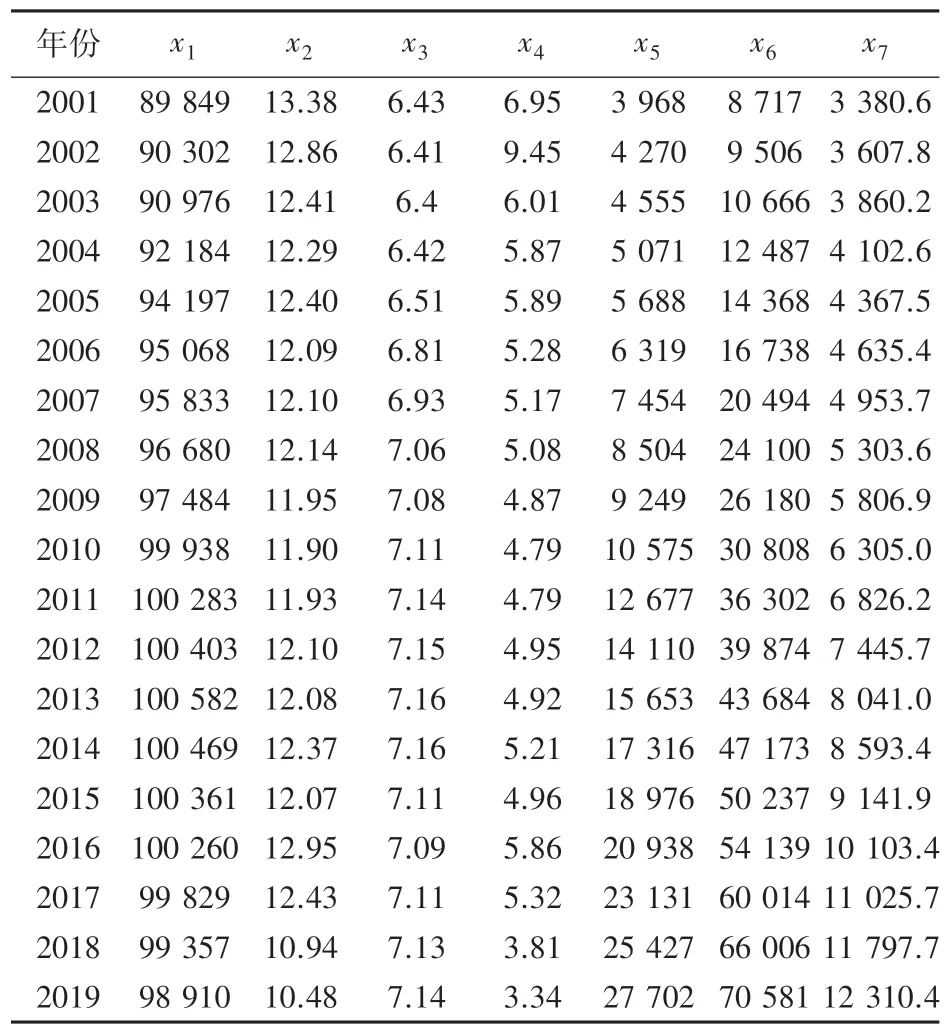
表1 2001-2019 年中国人口老龄化预测影响因素表Tab.1 Influencing factors of population aging prediction in China from 2001 to 2019
3.2 实验及结果
由于指标数量过多,各指标之间的数据级差异会对预测模型产生影响,因此将表1 的数据分别采用公式(3)和公式(4)的方法将数据统一到[0,1]区间内,从而保证指标的一致性。
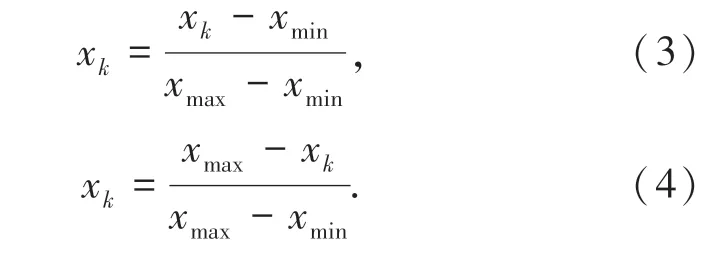
式中:xk为第k个指标归一化后的值,xmin与xmax分别为指标所在列的最小值与最大值。
归一化后的7 个指标x =(x1,x2,…,x7)作为SVR 模型的自变量,将65 岁以上人口(万人)作为因变量,从研究总体中选择2001~2003 年、2005~2006 年、2008~2012 年和2014~2018 年共15 组数据作为训练集,将2004 年、2007 年、2013 年和2019年的数据作为测试集。采用遗传算法,求得SVR 模型的最优参数组合C和g,由于各指标与输入输出量之间是非线性关系,而径向基(RBF)核函数适用于解决非线性关系的问题。因此,本文利用RBF作为核函数,实现非线性映射,最后将最优参数组合输入到SVR 模型中。参数寻优适应度曲线如图3 所示。
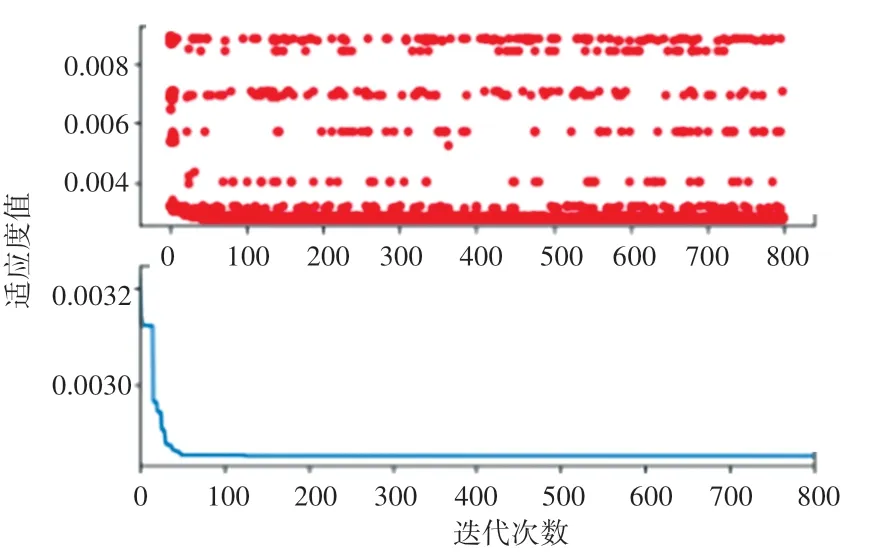
图3 参数寻优适应度曲线Fig.3 Fitness curve of parameter optimization
经过迭代后,SVR最优参数值为:C =279.569 307 539,g =0.000 354 796 650 669,此时训练集的适应度值(均方误差)为0.006 769 237 246 58。适应度曲线反映出每一代群体的最佳适应度和平均适应度的进化过程。从图3 中可以看出,随着迭代次数的增加,在后期基本达到了稳定的适应度值,收敛性能较好。
使用初始参数优化后的SVR 对训练集数据进行拟合,将拟合后的结果与真实值进行比较,与传统SVR 算法进行比较,实验结果见表2。

表2 模型评价Tab.2 Model evaluation
从表2 可以看出,本文提出的算法与传统SVR相比,平均绝对误差和均方误差更接近于数值0,可解释方差值和R方值更接近于数值1。将测试集数据输入到训练好的本文构建的模型中,与传统SVR算法作对比测试结果见表3。
从表3 可以看出,本文算法的预测值与真实值差值较传统SVR 预测差值相比较小。

表3 本文算法与传统SVR 预测结果比较Tab.3 Comparison of prediction results between the proposed algorithm and traditional SVR
实验结果表明:通过遗传算法优化初始参数的SVR 更加精确;本文提出的使用遗传算法优化支持向量机回归初始参数具有可实施性。
4 结束语
针对支持向量回归模型的分类精度依赖于初始参数选择的问题,本文设计了一种利用遗传算法优化支持向量回归模型初始参数的方法,并应用于中国老龄化人口预测问题上。实验结果表明,本文提出的优化方法的预测值优于传统SVR算法,为老龄化人口预测提供了切实可行的方法。

