非水反应高聚物-混凝土界面单调剪切特性及本构模拟
王钰轲,于博文,曹天才,郭成超,钟燕辉,石明生
(1.郑州大学 水利科学与工程学院,河南 郑州 450001;2.重大基础设施检测修复技术国家地方联合工程实验室,河南 郑州 450001;3.水利与交通基础设施安全防护河南省协同创新中心,河南 郑州 450001;4.中山大学 土木工程学院,广东 广州 510275)
土体与构造物界面结构在岩土工程中广泛存在,诸如:锚杆锚固段与土体间的黏聚力影响着锚杆加固的效果、混凝土衬砌与基土间的作用力影响着其稳定性;类似的还有土石坝中混凝土面板与垫层料之间的相互作用、钢筋与混凝土界面的力学相互作用、抗滑桩与土基界面的相互作用等。由于土体与不同构造物之间的力学特性差异,界面力学特征表现出非线性、大变形等现象且极易发生破坏,所以界面力学特性的研究显得尤为重要[1]。
以非水反应类双组份聚氨酯材料为基础的高聚物注浆技术是20世纪70年代初兴起的一种地基快速修复技术,其技术要点是将异氰脂酸与多元醇按照一定的配比,利用专用注浆设备在一定的压力和温度下混合,可快速发生化学反应,体积迅速膨胀并固化,以达到填补地基脱空,抬升基础的目的[2-3]。非水反应高聚物材料作为一种质量轻、强度高、膨胀性好[4]、耐久性好、反应快、防渗性能好、安全可靠的材料,近些年来在堤坝、尾矿库防渗[5-6]、路面修复[7-8]、基坑周围房屋沉降[9]、高铁无砟轨道[10]、地下管道沉降[11]、渗漏[12]、机场道面快干修复[13]等治理方面取得了很好的应用效果。
高聚物注浆材料由于性能优良,在隧道、公路、桥梁、铁路、大坝等基础设施的加固和维修方面展出广阔且良好的发展前景,国内诸多学者对高聚物注浆材料的宏观力学性能进行了研究。石明生等[14]根据高聚物注浆材料的特点,研制了高聚物注浆材料成型模具,制作了不同密度的高聚物试件,采用三点受力加荷方式,对不同密度的试件进行了弯曲性能试验研究;高翔等[15]运用单轴压缩试验,通过提取扫描电镜图中微泡孔的尺寸,并基于几何参数拟合材料抗压强度,从微观角度研究了高聚物材料的受力作用机理;李嘉等[16]首次将压电陶瓷弯曲元测试技术引入到高聚物注浆材料小应变动剪切模量测试中,研究了高聚物材料动剪切模量与密度及动、静弹性模量的关系;石明生等[17]通过量测不同密度高聚物试样的吸水率,以及测试干燥试样、饱水试样在一定温度范围内的体积变化,研究高聚物注浆材料的吸水特性及温度变化对材料体积的影响。
对于土工材料、筋土、砂土等与混凝土界面的剪切力学性能已经有诸多学者进行了研究。Wang等[18]运用一系列应变控制单调直接剪切试验、循环直接剪切试验和后循环直接剪切试验研究了小麦-混凝土在单调荷载和循环荷载作用下的界面行为;赵春凤等[19]通过对不同粗糙度的砂土-混凝土接触面在不同固结法向应力下进行的多组加、卸荷大型直剪试验,分析不同加、卸荷状态下接触面的力学特性,以及卸荷程度、粗糙度等对接触面软化特性和剪胀(缩)性的影响;周怡[20]为了研究含水率对板岩质砂土-混凝土界面的力学特征参数,采用大型直剪试验系统对不同含水率条件下的板岩质砂土-混凝土界面剪切特性进行试验;赵文等[21]基于数字图像相关技术,通过自主研制的可视化直剪容器,对砾砂与混凝土管接触面在常法向应力作用下的剪切力学特性进行较系统的试验研究。
土体与构造物之间的剪切应力-剪切位移变化曲线能够反映界面的受力变形规律,工程的设计是否具有可靠性,与验算所选取的本构有着密不可分的关系。关于土体-构造物之间接触面的本构模型已经有诸多学者进行了研究。Esterhuizen等[22]利用黏土-土工材料界面的剪切试验,得出筋土界面的剪切应力到达峰值后会出现明显的降低,即发生剪切软化现象,并提出了采用双曲线模型拟合峰值后的非线性行为。Seo等[23]运用扰动函数概念,利用试验结果得到的参数,对光滑土工膜(S-GM)与土工织物(GT)的界面,即S-GM/GT界面进行了反演预测,并提出将总应力场划分为峰值前和峰值后2个区域,以考虑应变软化对界面剪切行为的影响。Anubhav等[24]通过直剪试验机对2种不同的编织土工织物在土-土工织物界面上的剪切应力-剪切位移行为进行了研究,通过试验结果分析,提出了一个非线性本构模型,模型较好地预测了峰值前与峰值后的界面应力-应变关系。
以上研究多数是针对土体-土工材料的界面力学特性,以及采用非线性本构模型拟合界面的应力-应变关系曲线,但是关于成型高聚物与混凝土界面力学特性及本构关系的研究尚未见报道。作者基于室内直剪试验,研究了非水反应高聚物与混凝土试块的界面剪切特性;基于试验结果,分析了剪切速率、竖向应力对界面剪切应力-剪切位移曲线、抗剪强度、剪切模量的影响;借鉴Duncan-Chang双曲线模型,并进行稍微修改后,很好地模拟了界面应力-应变关系[25]。研究成果可为高聚物注浆材料在工程中的实际应用提供理论参考。
1 试 验
1.1 试验材料
所用高聚物成型试块儿的尺寸为50 mm×100 mm(高度×内径),发泡类,密度为0.2 g/cm3。混凝土拌合料采用混凝土入模养护14 d,按中国混凝土规范规定,该材料为不透水混凝土材料,混凝土砌块密度2 200 kg/m3,掺细砂、水泥、水。
1.2 试验内容及参数的定义
试验采用改进的直剪仪,直剪仪由加载系统、测量系统、剪切盒和支撑台组成。剪切盒由上箱和下箱的2个部分共同组成。下剪切盒由电动机驱动水平移动,上剪切盒固定在同一方向,样品接触尺寸为直径100 mm。垂直应力由杠杆施加,杠杆的重量取决于水平剪应力。该装置既可提供水平循环剪切,也可通过位移控制电机提供静态剪切。利用电动机将剪切速率控制在0.01~5.00 mm/min。水平位移和垂直位移由线性可变双变压器获得,相应的最大幅值分别为25和50 mm,精度为0.01 mm;所有的载荷和位移测量都由测量系统自动获取。图1为高聚物-混凝土单调直剪试验的装置及高聚物-混凝土试块,试验详细方案见表1。

图1 直剪仪装置Fig. 1 Direct shear apparatus

表1 单调直剪试验方案Tab. 1 Monotonic direct shear test schemes
对试验中的重要参数进行统一定义:取剪切应力与剪切位移关系曲线的剪切应力峰值为对应的界面抗剪强度τ,峰值后剪切应力极小值为界面对应的残余强度τ;抗剪强度与对应剪切位移的比值为剪切模量G;高聚物试块与混凝土界面的竖向应力为 σh。
2 试验结果及分析
2.1 剪切速率对剪应力-剪切位移曲线的影响
图2为竖向应力为50、100、150、200 kPa时,不同剪切速率下高聚物-混凝土界面的剪切位移与剪切应力的关系曲线。
由图2可知:不同剪切速率下,不同曲线均呈现出相似规律,即剪切应力均随着剪切位移的增大而增大,到达峰值后剪应力值均轻微减小后达到稳定状态,即表现出剪切软化特性;不同竖向应力下,分别控制不同的剪切速率,剪切应力随剪切位移的变化趋势是相似的,但是剪切应力的峰值不同,峰值剪切应力与残余剪切应力均随着竖向应力的增加呈上升趋势;同一竖向应力下,峰值剪切应力与残余剪切应力随着剪切速率的增加呈减小趋势,但是下降幅值不大。可以得出,剪切速率对高聚物-混凝土界面抗剪强度有一定的影响。

图2 不同竖向应力、不同剪切速率下高聚物-混凝土界面剪切应力-剪切位移曲线Fig. 2 Shear stress and shear displacement curves of polymer concrete interface under different vertical stress and different shear rates
2.2 竖向应力对剪应力-剪切位移曲线的影响
图3为剪切速率为1、2、3、4、5 mm/min时,高聚物-混凝土界面在不同竖向应力下的剪应力-剪切位移变化曲线。
从图3可以看出:高聚物-混凝土界面剪应力-剪切位移曲线在不同竖向应力下呈现出相似变化趋势,即剪应力均随着剪切位移的增加而增加,到达峰值剪切应力后又呈现轻微下降趋势直至平衡,表现出剪切软化的特性;在不同的竖向应力下,峰值剪切应力所对应的剪切位移有所不同;同一剪切速率下,随着竖向应力的增加峰值剪切应力所对应的剪切位移呈延后趋势,高聚物-混凝土界面峰值剪切应力随着竖向应力的增加而增加,而且增加幅值比较明显。可以得出,竖向应力对高聚物-混凝土界面的剪切强度有明显的影响。

图3 不同剪切速率、不同竖向应力下高聚物-混凝土界面剪应力-剪切位移曲线Fig. 3 Shear stress and shear displacement curves of polymer concrete interface under different vertical stress under different shear rates
2.3 剪切速率对抗剪强度的影响
根据不同剪切速率下高聚物-混凝土界面抗剪强度的试验结果,得到出高聚物-混凝土在竖向应力为50、100、150、200 kPa时,界面抗剪强度τ随着剪切速率v的变化情况,如图4所示。

图4 不同竖向应力、不同剪切速率下高聚物-混凝土界面抗剪强度变化曲线Fig. 4 Shear strength curves of polymer concrete interface under different shear rates and different vertical stresses
由图4可知:不同的竖向应力下,剪切速率为5 mm/min时的抗剪强度值较剪切速率为1 mm/min时的抗剪强度有所下降,下降幅度分别为14.69%、2.65%、6.01%、5.46%;同一竖向应力下,抗剪强度值随着剪切速率的增加而近似线性递减;不同竖向应力下,剪切速率为1 mm/min时,抗剪强度随着竖向应力的增加而增加,增加的幅度分别为60.57%、46.37%、27.09%,增加幅值呈现下降趋势,但是整体抗剪强度值呈现上升趋势。由以上数据分析可得:不同的竖向应力下,抗剪强度随着剪切速率的增加而近似呈线性下降趋势;同一竖向应力下,高聚物-混凝土界面抗剪强度随着剪切速率的增加而减小;同一的剪切速率下,抗剪强度又随着竖向应力的增加而呈上升趋势。可以得出结论,剪切速率与竖向应力对高聚物-混凝土界面抗剪强度均有一定的影响。
2.4 竖向应力对抗剪强度的影响
图5为不同剪切速率下高聚物-混凝土界面的抗剪强度与竖向应力的拟合直线。

图5 不同剪切速率下高聚物-混凝土界面的抗剪强度随竖向应力的变化Fig. 5 Variation of shear strength of polymer concrete interface with vertical stress under different shear rates
由图5可知,高聚物-混凝土界面的抗剪强度随着竖向应力的增大呈近似线性增加,在不同的剪切速率1、2、3、4、5 mm/min下,拟合直线相关系数分别为0.999 9、0.999 9、0.999 8、0.999 5、0.999 9。由此看出拟合度比较好,表明界面抗剪强度与竖向应力有着很好的相关性。遵循摩尔-库伦准则:

式中: τ为高聚物试块与混凝土界面抗剪强度,单位为kPa; σh为高聚物试块与混凝土界面的竖向应力,单位为kPa;φp为高聚物试块与混凝土界面有效摩擦角;cp为高聚物试块与混凝土界面似黏聚力,单位为kPa。为了分析高聚物试块与混凝土界面的抗剪强度参数受剪切速率的影响状况,由不同剪切速率下的拟合曲线斜率可得,拟合曲线斜率随着剪切速率的增加而呈现细微下降趋势,也即速率为1 mm/min时的直线斜率最大,速率为5 mm/min时的斜率最小。
剪切分别为1、2、3、4、5 mm/min时的界面似黏聚力大小为7.54、7.62、7.63、7.39、7.38 kPa,对应剪切速率下的摩擦角分别为23.94°、23.59°、23.35°、23.15°、22.84°。可以看出,摩擦角大小随着速率的增加轻微减小,说明了剪切速率对摩擦角和似黏聚力影响较小。
2.5 剪切速率对剪切模量值的影响
图6为竖向应力分别为50、100、150、200 kPa时,高聚物-混凝土界面的剪切模量随剪切速率的变化曲线。

图6 不同竖向应力下高聚物-混凝土界面的剪切模量随剪切速率的变化曲线Fig. 6 Shear modulus versus shear rate curves of polymer concrete interface under different vertical stresses
由图6可知:不同竖向压力下,剪切模量值随着剪切速率呈相似变化趋势,即近似线性下降;剪切速率为1 mm/min时,竖向应力为100、150、200 kPa剪切模量值增加幅度为43.51%、26.98%、27.42%;剪切速率为5 mm/min时,剪切模量值的增加幅度分别为38.754%、30.733%、21.030%;剪切模量值随着竖向应力的增加而呈整体上升趋势。由以上数据分析可以得出,各竖向应力下,高聚物-混凝土界面剪切模量值随着剪切速率的增加而不断减小,减小幅值明显。
2.6 竖向应力对剪切模量值的影响
图7为不同剪切速率下,高聚物-混凝土界面剪切模量与竖向应力的关系曲线。由图7可知:不同剪切速率下,剪切模量值随着竖向应力的增加而呈现上升趋势;同一竖向应力下,剪切模量值又随着剪切速率的增加而不断减小。可以得出,竖向应力以及剪切速率对高聚物-混凝土的剪切模量都有一定的影响。

图7 不同剪切速率下高聚物-混凝土界面的剪切模量与竖向应力关系曲线Fig. 7 Relationship between shear modulus and vertical stress of polymer concrete interface under different shear rates
2.7 剪切速率对残余强度的影响
图8为高聚物-混凝土界面在不同竖向应力下,界面残余抗剪强度τr随着剪切速率的变化曲线。

图8 不同竖向应力、不同剪切速率下高聚物-混凝土界面残余抗剪强度变化曲线Fig. 8 Variation curves of residual shear strength of polymer concrete interface under different shear rates under different vertical stresses
由图8可知:同一竖向应力下,残余抗剪强度随着剪切速率的增加而呈现下降趋势,下降幅值较小;竖向应力为200 kPa,剪切速率为2 mm/min时,残余抗剪强度出现轻微上升,但是随后随着剪切速率的增加,残余抗剪强度又随后呈现下降趋势;同一剪切速率下,残余抗剪强度随着竖向应力的增加而呈现上升趋势,增加幅值较明显。可以得出,剪切速率与竖向应力对高聚物-混凝土界面残余抗剪强度有一定的影响。
2.8 竖向应力对残余强度的影响
图9为不同剪切速率下高聚物-混凝土界面的残余抗剪与竖向应力的强度拟合直线。
由图9可知:高聚物-混凝土界面的残余抗剪强度随着竖向应力的增大呈近似线性增加,在不同的剪切速率1、2、3、4、5 mm/min下,拟合直线相关系数分别为0.954 8、0.976 9、0.999 6、0.996 8、0.996 5,拟合度比较好,表明界面残余抗剪强度与竖向应力有着很好的相关性。满足摩尔-库伦准则:

图9 不同剪切速率下高聚物-混凝土界面抗剪强度与竖向应力的关系Fig. 9 Relationship between shear strength and vertical stress of polymer concrete interface under different shear rates

式中: τr为高聚物试块与混凝土界面残余抗剪强度,单位为kPa; σh为高聚物试块与混凝土界面的竖向应力,单位为kPa;φr为高聚物试块与混凝土界面残余摩擦角;cr为高聚物试块与混凝土界面残余似黏聚力,单位为kPa。为了分析高聚物试块与混凝土界面的残余抗剪强度参数受剪切速率的影响情况,由不同剪切速率下的拟合曲线斜率可得,拟合曲线斜率随着剪切速率的增加几乎不发生变化,剪切速率为5 mm/min时,斜率轻微下降。
剪切速率分别1、2、3、4、5 mm/min时的残余似黏聚力大小为0.61、0.32、0.19、0.19、0.18 kPa,在对应剪切速率下的残余摩擦角分别为0.77°、0.89°、0.92°、0.88°、0.87°。可以看出,残余摩擦角大小近似为0,残余似黏聚力近似为0,说明了残余摩擦角和残余似黏聚力受剪切速率的影响较小。
3 非水反应高聚物-混凝土界面非线性本构模型
土工合成材料界面的力学特性受材料类型、制作方式、环境、温度等条件的约束,在直剪试验中不同材料的接触面之间会呈现不同的应力-应变曲线,即使呈现出应变软化的界面,其剪切应力-剪切位移曲线也在某种程度上表现出很大的差异。因此,针对不同的界面选择能够较好适应自身试验结果的非线性模型是保证计算精确度的关键所在。充分考虑界面的应变软化特性,并针对本文试验应力-应变曲线,以界面剪切应力峰值对应的剪切位移为分界点,采用Duncan-Chang双曲线模型分别模拟峰值应力前与峰值应力后的应力-应变曲线,如图10所示。在峰值应力前的界面剪切应力-剪切位移曲线采用Duncan-Chang双曲线模型模拟;在峰值剪切应力后,也即是应变软化阶段,以剪切应力峰值点为原点建立坐标系,取双曲线的一部分进行倒置,以此模拟应变软化阶段的应力-应变曲线。

图10 本构模型示意图Fig. 10 Schematic diagram of constitutive model
3.1 剪切应力-剪切位移曲线峰值前阶段
在峰值应力前,界面剪切应力-剪切应变关系采用双曲线进行模拟,公式如下:


建立模型还需引入破坏比,定义峰值剪切应力与最终剪切应力的比值为破坏比Rf,即破坏比公式为:

联立式(3)~(7),用于描述本模型的峰值前剪切应力-剪切位移曲线的瞬时剪切模量表达式如下:

3.2 应变软化阶段模型

联立式(9)~(13)可得应变软化阶段的剪切刚度:

3.3 界面模型参数
为了验证本文所选模型的可靠性,拟合非水反应高聚物-混凝土界面直剪试验参数,整个界面的模型参数如表2所示。
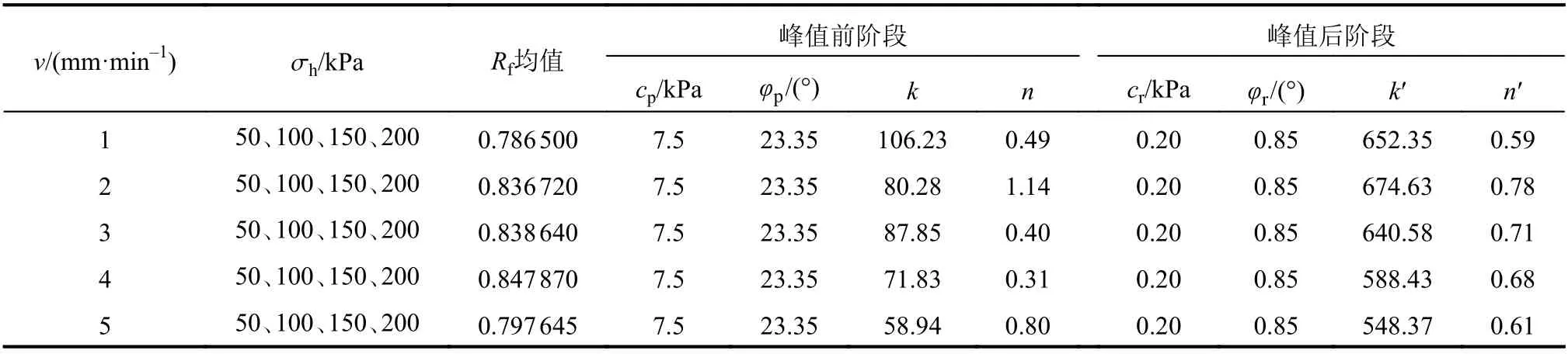
表2 界面模型参数Tab. 2 Interface model parameters
3.4 界面模型的验证
图11为高聚物-混凝土试块界面试验值与模拟值的对比。由图11可知:同一速率下,随着界面竖向应力的增加,界面剪切强度与剪切位移曲线的试验值与模拟值非常接近,不同速率、不同正向应力下均表现出了相似的拟合程度,表明该双曲线本构模型能够较好地模拟剪切软化型应力-应变曲线。

图11 界面试验值与本构模型模拟对比Fig. 11 Comparison of interface test values and constitutive model simulation
4 结 论
采用改进的室内直剪仪,针对非水反应物类高聚物-混凝土界面剪切特性进行了一系列单调直剪试验,研究了不同类因素对高聚物-混凝土界面界面剪切特性的影响,并结合试验结果,采用双曲线本构模型对高聚物-混凝土界面剪切特性进行了描述,得到了以下几点结论:
1)剪切速率对在单调直剪条件下高聚物-混凝土界面剪切的特性具有一定影响,在相同的竖向应力下,随着剪切速率的增加,高聚物-土工布界面的剪切应力峰值略有变化,整体上呈减小的趋势,高聚物-混凝土界面随着剪切位移的增加发生了剪切软化现象;竖向应力对高聚物-混凝土界面剪切特性的具有较为显著影响,在相同剪切速率下,随着竖向应力的增加,高聚物-混凝土界面剪切应力峰值呈现较为显著的增加趋势。但是在相同竖向应力条件下,剪切速率对高聚物-混凝土界面的抗剪强度以及残余强度影响不大。
2)本文所涉及的单调直剪试验中,高聚物-混凝土界面的残余似黏聚力的值较小,可以忽略;黏聚力影响较小但不可以忽略,并且其摩擦角一定程度上受到剪切速率的影响也较小。
3)在相同的各竖向应力作用下,随着剪切速率的增加,高聚物-混凝土界面的剪切模量、抗剪强度以及残余强度呈逐渐减小的趋势,但减小幅度不大;在相同的剪切速率下,随着竖向应力的增加剪切模量值、抗剪强度以及残余强度呈现上升的趋势,趋势较为明显,即剪切速率对高聚物-混凝土界面的剪切模量影响较小而竖向应力对高聚物-混凝土界面的剪切模量、抗剪强度以及残余强度影响较大。
4)针对应变软化型的高聚物-混凝土界面特性,运用数学公式描述,系统地阐述了双曲线本构模型的构建过程。经过初步验证,模型的剪切强度与剪切位移曲线试验值与模拟值有较好的拟合度。

