基于挠度曲率面积差的桥梁结构损伤识别方法

吴 桐，唐 亮，周志祥

(1.重庆交通大学 省部共建山区桥梁及隧道工程国家重点实验室，重庆 400074；2.深圳大学 土木与交通工程学院，广东 深圳 518060)

桥梁结构作为公路交通运输中不可或缺的一部分，在运营中极易受到来自外部环境和桥梁自身结构和材料老化等不利因素带来的影响，使其无法达到设计预期寿命。若未及时检测到结构损伤，则可能导致损伤加剧，甚至引发灾难性后果。因此，结构健康监测（structural health monitoring，SHM）对于保证桥梁结构在其使用中的安全至关重要[1-2]。

根据桥梁结构整体安全状态评估或损失识别方法所采取的数据类型，可以分为基于静态和基于动态参量的两大类。静态参量类型主要包括位移、转角、曲率和应变等，其中，位移的曲率对结构损伤的敏感性较好，因此利用位移的曲率及其衍生参数进行损伤识别受到广泛关注[3-4]。Yam等[5]首先基于有限元模型分析了板结构静力参数，如挠度、挠度斜率及挠度曲率的损伤因子对损伤的敏感性，发现挠度曲率比挠度对结构损伤更加敏感。陈淮等[6]根据摄动有限元法原理，提出基于测点间位移差的变化进行吊杆损伤识别的方法，并在实桥上验证了该方法的有效性。吴杰[7]在实验室对一座有机玻璃模型桥进行静力加载试验，利用挠度曲率识别了结构损伤。王艺霖等[8]利用差分曲率差值指标对结构进行损伤定位，提出测点优化布置方式。陈孝珍等[9]基于灰色理论的相关性分析方法，将静态位移曲率置信因子用于静力损伤定位，在两端固支梁上验证了该方法的有效性。Wang等[10]提出了利用静态挠度的结构损伤识别算法：首先，运用损伤指标对结构的损伤进行定位；然后，使用迭代计算求解非线性优化问题，预估损伤程度。Banan等[11]将以残余力误差和挠度误差最小为优化目标函数的优化问题转化为结构损伤的识别问题，并研究求解优化方程的迭代算法；因为测量得到的信息不多，再加上测量时的噪声影响，所以，利用算法建立了一个并不很准确的非线性方程。崔飞等[12-13]利用梯度法、Gauss-Newton（G-N）法、Monte-Carlo法解决了上述非线性方程不很准确的问题。Liang等[14]对具有损伤的三跨连续梁模型进行理论分析，发现挠度影响线及1阶导数是连续的，但其曲率在损伤部位附近不是连续的；根据这一性质，利用小波变换可以求出挠度影响线曲率的不连续点，从而识别损伤位置。姜腾蛟[15]通过对钢-混凝土组合梁在多种损伤工况下的加载试验，开展了基于桥面全息变形监测的损伤识别方法研究；利用提出的基于改进阈值函数的小波降噪处理算法对不同损伤状态的特征曲率信号进行降噪处理。Le等[16]利用虚功原理，将挠度曲率作为损伤位置和损伤程度的函数，提出了一种无需优化算法和有限元计算的损伤识别方法。

在利用动态参数进行损伤识别的方法中，基于模态振型曲率变化的损伤定位法具有原理简单、结果直观、效率较高的优点。Pandey等[17]提出用曲率模态进行损伤识别的方法，并采用中心差分近似法，由位移模态计算曲率模态。Wahab等[18]采用曲率模态法对一个实桥进行了损伤识别，研究了模态曲率变化在预应力混凝土桥梁损伤检测中的应用。贺文宇等[19]采用希尔伯特变换，从移动车辆响应中提取出高分辨率的损伤桥梁振型，采用区域振型曲率替代传统的振型曲率，综合损伤前后的区域振型曲率定义损伤定位指标。曾滨等[20]采用能量-损伤证据矩阵理论，融合叠加曲率模态改变率和模态柔度差曲率两项指标的损伤识别结果，实现了对张弦桁架多位置的损伤识别。He等[21]提出了一种基于曲率振型和频率扰动的结构损伤识别方法，根据结构在未损伤和损伤状态下曲率模态形状的差异，建立了损伤方程。

综上，静态位移曲率包含有关刚度降低和相应损伤的决定性信息[22-23]，基于静力参数的损伤识别方法都需要在结构上布置大密度的测点，并获取结构在相同条件（环境条件、荷载工况）下损伤前后的测试数据进行识别，这限制了其在实际桥梁损伤识别中的应用。因此，近年来基于静态参数的方法发展较为缓慢。现有的损伤识别方法很多都是针对特定的损伤类型，只有当损伤累积到了一定程度才能够识别，而初期出现结构损伤的程度通常是微小的，如果不及时处理，随着桥梁的运营，这些微小损伤可能会不断发展积累，甚至造成灾难性的后果。由此，提出一种利用挠度曲率面积差进行损伤识别的方法，将损伤前后的曲率曲线所包围的面积作为损伤识别参数。分析结果表明，该方法能够准确识别结构中不同程度和数量的损伤，特别对微小程度的损伤也有较高的灵敏性。

1 理论模型

1.1 挠度曲率的面积差方法

由结构力学[24]可知，曲率与结构刚度之间的关系为：

式中，w′′为结构在荷载作用下的挠度曲率，M(x)为荷载引起的弯矩，EI为结构抗弯刚度。

从式（1）可以看出，在外荷载不变的情况下，当结构刚度发生改变，必然会引起曲率的改变。本文通过研究结构挠度及其1、2阶导数（转角和曲率）之间的关系，引入挠度曲率面积差参数。如图1所示，以一简支梁有限元模型展示挠度曲率面积差参数计算分析的过程及结果。

图1 简支梁基本图示Fig. 1 Basic diagram of simply supported beam model

如图1所示长度为L的简支梁，将其纵向等分为n个长度为a的单元，单元编号从左至右依次为1、2、3、 ···、n，共n个单元。假设第i个单元发生了损伤，通过计算可以得到荷载作用下各节点损伤前后的位移、转角和曲率，分别见图2～4。

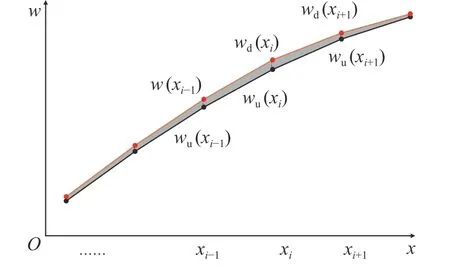
图2 损伤前后挠度曲线Fig. 2 Deflection curves before and after damage

图3 损伤前后转角曲线Fig. 3 Inclination curves before and after damage

图4 损伤前后曲率曲线Fig. 4 Curvature curves before and after damage

由图2～4可以看出，损伤前与损伤后的各参数曲线之间包围着微小面积，该面积也被分为n个单元，分别为A1、A2、 ···、An，则第i个单元的面积差参数定义为第i个单元面积的平方在所有单元面积平方和中所占比例：

1.2 数值模拟

1.2.1 简支梁模型

在桥梁专用结构分析软件Midas/Civil中，建立一简支T梁的有限元模型。梁的几何、材料和截面特性分别为：梁长L=20 m，弹性模量E=3.25×104MPa，密度ρ=2 500 kg/m3，面积A=0.881 m2，惯性矩I=0.431 m4。纵向共划分为20个长度为1 m的区段。简支梁模型如图5所示。

图5 简支梁模型基本图示Fig. 5 Basic diagram of simply supported beam model

对该模型桥设置了多程度、多位置的损伤，其中，用单元弹性模量降低以模拟结构局部刚度损伤，各损伤具体信息如表1所示。表1中，工况1-1为未损伤工况，工况1-2～1-5为6#单元不同损伤程度的工况，工况1-6和1-7为不同损伤位置的工况。

表1 各损伤工况Tab. 1 Damage scenarios

计算得到在跨中500 kN集中荷载作用下简支梁的挠度后，利用数值求导方法，得到了不同工况下各节点的曲率曲线，如图6和7所示。图6中，各工况的曲率曲线各有两处突变，分别为损伤单元（6#单元）和集中荷载作用位置（跨中）。其中，损伤位置处曲率曲线的突变程度随着单元损伤程度的加剧呈非线性增加。

图6 不同损伤程度工况下的曲率Fig. 6 Curvatures under different damage severities

图7中：除了集中荷载作用处之外，各工况曲率曲线的突变数与损伤单元的数目一致；但当集中荷载作用处单元也发生损伤时，突变发生了叠加。由此，直接利用集中荷载作用下的曲率曲线识别损伤存在以下不足：1）对程度较低的损伤识别效果不明显；2）集中荷载作用处的损伤可能会被忽略。

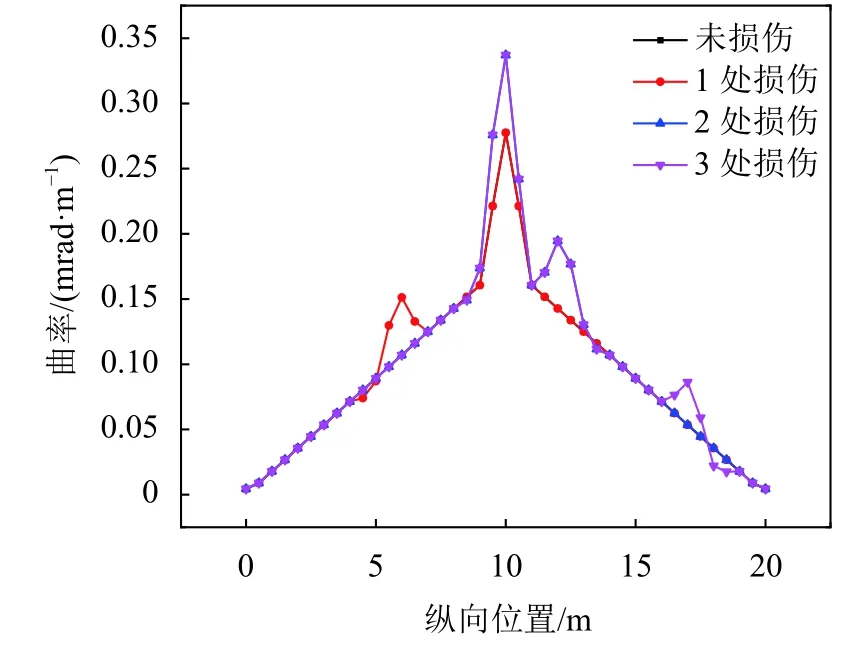
图7 不同损伤数量工况下的曲率Fig. 7 Curvatures under different damage numbers

为了准确判断结构是否损伤，对结构的挠度曲线进行数值求导得到各节点的转角，再利用式（13）直接计算各单元曲率面积差 ΔAκ值，如图8所示。

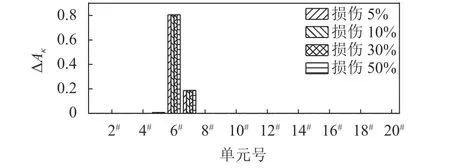
图8 不同损伤程度工况下各单元曲率ΔAκ值Fig. 8 ΔAκ values under different severities of damage

由图8可以看出：在集中荷载作用下，各损伤工况下曲率 ΔAκ峰值均明显指示了损伤位置所在；且无论是5%程度的微小损伤或50%的严重损伤，曲率ΔAκ值均约为0.7， ΔAκ值对微小损伤展现出了很高的灵敏性；同时，在集中荷载作用位置（纵向10 m处），曲率ΔAκ值并无改变，没有受到集中荷载的影响。

当结构中存在局部刚度损伤时，无论是微小损伤（ΔEI=5%），还是较大程度损伤（ΔEI=50%），通过荷载作用下损伤前后曲率面积差值（ ΔAκ）都可以较准确地识别出损伤位置。

图9为工况下各单元的曲率 ΔAκ值，图10为工况7下各单元的曲率 ΔAκ值。当结构中存在不同数量的局部刚度损伤时，在损伤对应位置处， ΔAκ值会出现局部极值。只有1处损伤时， ΔAκ值在损伤位置处最大（图8）；当存在多处损伤时（图9和10）， ΔAκ值在损伤对应位置出现峰值，且靠近跨中的损伤，其 ΔAκ值大于靠近支座处的损伤。

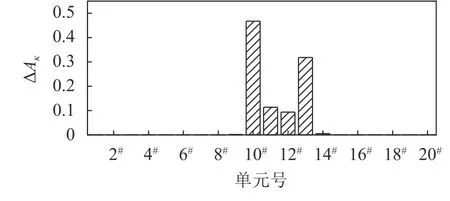
图9 2处损伤工况下各单元曲率ΔAκ值Fig. 9 ΔAκ values of each element under two damages

图10 3处损伤工况下各单元曲率ΔAκ值Fig. 10 ΔAκ values of each element under three damages

1.2.2 测点数量对识别效果的影响

第1.2.1节中计算 ΔAκ值时，单元长度为1 m，单元长度与梁长的比值为1/20，即沿单元长度方向，挠度测点密度为每隔1 m测量1个点的挠度，测点总数量为21。由此，计算单元长度越短，即挠度测点的密度越大，损伤位置的识别越准确。因此，通过改变挠度测点的密度，来分析单元长度对识别效果的影响。

在第1.2.1节中选择工况1-5，令计算单元长度分别为1、2和4 m，即单元长度与梁长的比值分别为1/20、1/10和1/5，也即沿单元长度方向分别每隔1、2和4 m布置一个挠度测点，通过求导计算各点的转角值，再利用式（13）计算各单元的 ΔAκ值，绘制成柱状图，如图11～13所示。

由图11～13可以看出：无论是单元长度的如何，即测点布置的疏密如何，损伤带来的 ΔAκ值增大总能在其范围内的测点体现出来，即使测点数量很少，也能定位损伤；测点密度越大，损伤的位置也越准确。

图11 单元长度为1 m的ΔAκ值Fig. 11 ΔAκ values with element length of 1 m

图12 单元长度为2 m的ΔAκ值Fig. 12 ΔAκ values with element length of 2 m

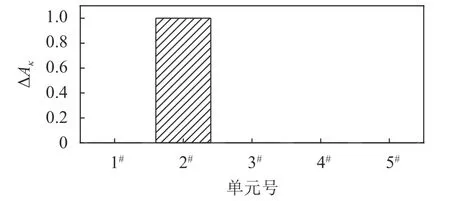
图13 单元长度为4 m的ΔAκ值Fig. 13 ΔAκ values with element length of 4 m

2 室内模型试验

2.1 试验概况

挠度曲率面积差参数在理想状况下可以准确定位结构中的微小损伤（ΔEI=5%），损伤识别不受曲率面积差方法理论本身的限制，而仅限于所应用测量技术的精度。因为要计算转角和曲率，需要对挠度值进行1次和2次求导，则噪声对测量精度的影响也会逐渐增大。所以，利用该方法进行损伤识别的前提条件包括：1）较高的挠度测量点密度，以便能够得到连续的挠度曲线；2）较高的挠度测量精度；3）适用于现场桥梁试验。

综上，分别选择Leica Scan Station P50 3维激光扫描仪及百分表获取模型桥的挠度。Leica Scan Station P50 3维激光扫描仪采用WFD波形数字化技术，扫描距离小于10 m时的精度为0.8 mm。试验时，对模型桥的扫描点云密度均设置为0.8 mm，重复扫描可提高点云精度，每次扫描时长约10 min。

有机玻璃模型桥为简支T梁桥，长1.6 m，宽0.8 m。横向布置5片T梁，编号为1#～5#梁；沿纵桥向分别在两端支座截面、L/4截面、跨中截面、3L/4截面布置5道横隔梁。桥梁各部分具体尺寸如图14所示。有机玻璃材料的密度约为1.18～1.19 g/cm3，属于刚性硬质材料。拉伸压缩强度约为50～77 MPa，弯曲强度为90～130 MPa。在室温环境下，有机玻璃的力学破坏形态表现出脆而硬、断面光滑的特点。断裂伸长率比较小，大概为2%～3%。为了明确该批次有机玻璃材料的弹性模量，方便后期对其进行有限元建模计算，加载前对该批次有机玻璃随机抽取3根棒状材料，利用万能试验机进行弹模测试，得到平均弹模为2 050 MPa。

图14 简支T型梁桥平面、横断面及纵断面图Fig. 14 Plane，cross section and profile maps of simply supported T-beam bridge

试验共设置2种加载及数据采集方式：1）在梁下进行加载，在每片主梁肋板上沿梁长方向均匀地用长尾夹挂载质量为2 kg的砝码，用以模拟主梁上的均布荷载，如图15所示，用3维激光扫描仪采集桥面点云；2）在桥面作用集中荷载，主梁下安装7个百分表读取变形数据，如图16所示。具体加载及测试工况见表2。

图15 3维激光扫描仪采集桥面形态数据Fig. 15 Data acquisition of by 3D laser scanner

图16 集中荷载加载Fig. 16 Local defect of model bridge

表2 模型桥详细加载工况Tab. 2 Loading scenarios of model bridge

对于工况2-1～2-2，利用3维激光扫描仪采集无损伤工况下模型桥的桥面点云数据作为基准数据。在1#T梁距左侧支座距离0.6 m处，人为制造一处高约25 mm、宽约5 mm的缺陷，再次进行3维激光扫描得到损伤后的点云数据。对于工况3-1～3-4，首先，读取加载后未损伤工况下百分表的挠度数据作为基准数据；然后，在5#T梁距左侧支座0.91 m处人为切割一条裂缝，如图17所示。

图17 1#梁缺陷具体图示Fig. 17 Photo of local defect of model bridge

利用裂缝测宽仪测得该裂缝宽0.6 mm、高80 mm，如图18所示，再次读取损伤后百分表的挠度数据，用损伤状态数据减去无损基准数据，即为损伤识别的基础数据。

图18 5#梁裂缝宽度测量Fig. 18 Measurement of 5# beam crack width

2.2 挠度曲率面积差识别模型桥损伤

2.2.1 点云数据处理

Leica Scan Station P50扫描的数据包含海量的数据点，如图19所示，除了所需要的桥面点云之外，还包含大量没有用处的背景点；并且，由于桥面的不平顺以及测量系统本身的影响，不可避免地在桥面真实数据点中混有不合理的噪声点，这些噪声点会导致数据采集的效果变差，误差增大，对后续桥面重构以及数据分析有很大影响，不便于点云数据的后期处理。所以，在提取变形数据之前，必须进行去噪、平滑滤波和曲面重构等处理过程，以得到桥面全息形态，如图20所示。点云数据的具体处理流程如图21所示。

图19 原始点云图Fig. 19 Original data point cloud map

图20 点云插值得到桥梁挠曲面云图Fig. 20 Surface of bridge based on interpolation

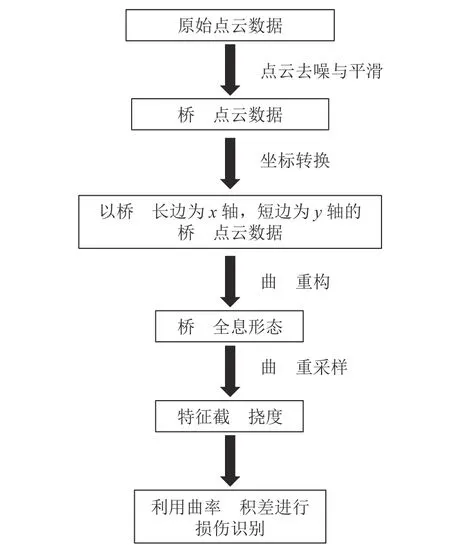
图21 点云数据处理流程图Fig. 21 Flow chart of point cloud data processing

2.2.2 3维激光扫描数据的损伤识别

针对工况2-1～2-2，在损伤的1#T梁纵向挠度曲线上每隔0.1 m，划分一个单元，则纵向挠度曲线可等分为16个单元，划分后的挠度曲线如图22所示。对该挠度曲线数值求导，得到转角和曲率曲线，分别如图23、24所示。

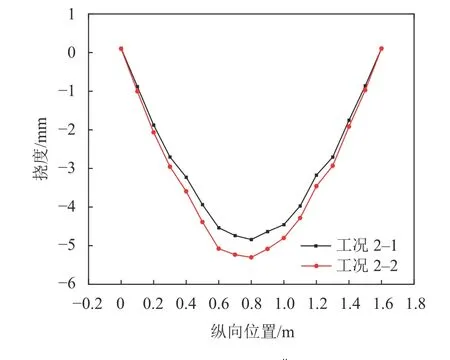
图22 模型桥损伤前后1#梁挠度曲线Fig. 22 Deflection curves of 1# beam of the model bridge before and after damaged

图23 模型桥损伤前后1#梁转角曲线Fig. 23 Angle of inclination curves of 1# beam of the model bridge before and after damaged

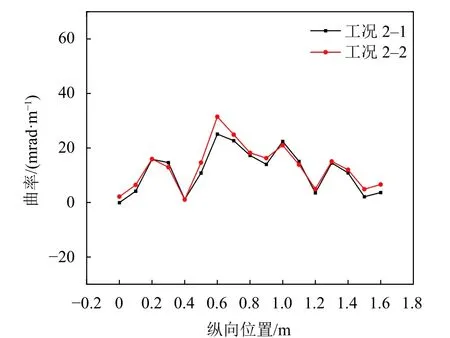
图24 模型桥损伤前后1#梁曲率曲线Fig. 24 Curvature curves of 1# beam of the model bridge before and after damaged

根据式（13）计算得到各单元的 ΔAκ值，如图25所示。由图25可以看出，该值在6#、7#单元处明显大于其余单元，在实际情况中，缺陷位于距1#梁左端的0.6 m处，且缺陷宽度约为5 mm，计算分析损伤定位与实际一致。

图25 划分为16单元的Δ Aκ值Fig. 25 Δ Aκ values of 16 elements

测点密度与损伤定位效果直接相关。在1#T梁纵向挠度曲线上每隔0.2和0.4 m划分一个单元，即纵向挠度曲线等分为8个单元和4个单元。数值求导计算得到转角值，之后根据式（13）计算得到各单元的ΔAκ值，其中，划分为8单元的 ΔAκ值如图26所示，划分为4单元的 ΔAκ值如图27所示。从图26和27可以看到，单元的划分疏密有别，但对应的 ΔAκ峰值单元均指示了损伤位置。

图26 划分为8单元的ΔAκ值Fig. 26 ΔAκ values of 8 elements

图27 划分为4单元的ΔAκ值Fig. 27 ΔAκ values of 4 elements

2.2.3 百分表数据的损伤识别

对于工况3-1～3-4，百分表将5#T梁挠度曲线等分为8个单元。对该挠度曲线的数值求导，可以得到转角和曲率分别如图28～30所示；根据式（13）计算得到各单元的 ΔAκ值，如图31所示。由图31可以看出，在不同荷载等级下，5#单元明显大于其余单元，损伤定位结果与实际一致。

图28 模型桥损伤前后5#梁挠度曲线Fig. 28 Deflection curves of 5# beam of the model bridge before and after damaged

图29 模型桥损伤前后5#梁转角曲线Fig. 29 Angle of inclination curves of 5# beam of the model bridge before and after damaged

图30 模型桥损伤前后5#梁曲率曲线Fig. 30 Curvature curves of 5# beam of the model bridge before and after damaged

图31 划分为8单元的ΔAκ值Fig. 31 ΔAκ values of 8 elements

3 结论与展望

为寻求一种比人工巡检更客观高效的桥梁安全检查方法，根据挠度、转角和曲率三者之间的关系，推导了挠度曲率面积差参数 ΔAκ的计算公式用于定位结构损伤，并利用室内试验对该方法的有效性进行了验证，得到以下结论：

1）所提出的 ΔAκ特征值理论上可准确定位结构中不同程度（5%～50%）的局部刚度损伤，特别是在结构微小损伤程度下仍有较强的敏感性。

2） ΔAκ特征值可直接由转角值计算得出，而转角值可以通过转角传感器直接测量得到，或通过挠度曲线1次求导得到，减小了2次求导计算曲率带来的数值求导和曲线拟合误差放大效应。

3）对实验室一座有机玻璃模型桥进行加载试验，利用3维激光扫描仪得到了模型桥损伤前后的挠曲面点云数据，提取1#梁损伤前后的挠度曲线；利用传统百分表获取了5#梁损伤前后的挠度曲线，计算了各单元 ΔAκ特征值，有效定位了结构损伤位置。

中小桥梁结构在日常安全巡检中多采用检查人员沿桥面目视打分的方法，极大依赖于检查人员的经验和素质，缺乏可量化的科学依据。本文所提出挠度曲率面积差（ ΔAκ）特征可通过载荷作用下测量桥面挠度变化来分析结构刚度损伤状况，可使桥梁结构刚度损伤判断有客观数据和量化指标——桥面挠度变化及挠度曲率面积差（ ΔAκ），为桥梁日常安全巡检的客观高效化提供了一种有效方法。

随着测量技术和设备的提高，目前利用摄影测量、数字图像相关方法（DIC）等都能够较方便和高效地获取桥梁密集测点的变形，这也是本文研究方法的技术基础。本文旨在解决量大面广的中小桥经常性安全检查量化、高效、客观性问题，所以研究对象选取的是力学状态较清晰的简支梁与连续梁桥，但桥梁结构体系类别繁多，且即使相同类别结构又有细微差异，面对复杂或者组合体系桥梁本文提出的方法是否同样适用，还需要进一步的研究与探讨。