一种基于CORDIC算法的混合跳扩频跟踪同步方法
陈 雷,王 涛,田晓燕,张锁良
(1.河北大学 电子信息工程学院,河北 保定 071002;2.北京邮电大学 电子工程学院,北京 100876)
0 引 言
混合跳扩频通信系统是国内外公认的最富有生命力的抗干扰系统,在近十几年的研究发展中得到了广泛应用[1-2]。在近几年的研究中,研究者们逐步确定了混合跳扩频调制解调方案,分析了信号设计与参数设定对系统的影响[3],主要对系统信息捕获以及跟踪同步方面展开研究[4-5]。
在系统跟踪同步方面,文献[6]提出一种四相鉴频方法,通过对大步长进行牵引,利用锁相环(Phase Locked Loop,PLL)和锁频环(Frequency Lock Loop,FLL)对高动态信号进行精确跟踪,提高了频偏的跟踪范围。文献[7]在跳频速率3 000 hop/s、跳频带宽84.48 MHz的情况下,利用早迟门位同步环完成定时同步,结合多普勒基准频率与IQ相关积分鉴频算法对本地载波进行调整完成载波同步,解决了载波相位不连续问题,可适应大频偏场景。文献[8]提出了一种FLL+PLL结合快速傅里叶变换(Fast Fourier Transform,FFT)的载波跟踪方法,可以有效提高载波捕获和跟踪的成功概率,缩短载波同步的时间。文献[9]在跳频速率9 000 hop/s,跳频带宽90 MHz的情况下,利用IQ两路相关积分、低通滤波器、早迟门位同步环对系统误差进行了整合,利用PLL与FLL完成统一补偿,实现系统同步。文献[10]提出了一种基于PLL环路的相位跟踪算法,可以有效剥离信号中的扩频码和扰码,鉴相器输出结果不受赋值影响,提高了误差提取的准确度。
经过以上分析可以看出,在近几年的研究中,研究者们面对的跳频速率均为每秒几千跳,跳频带宽在100 MHz以内,误差范围较小,浮动频率较低。在误差补偿方面,采用的是先计算再补偿的方式,利用反馈环路调整本地信号使系统达到同步,但没有考虑上下行时钟引起的系统误差,实际应用存在一定局限性。在系统内部,由于上下行时钟不同源,会产生内部误差,并且误差的浮动频率和范围与系统跳频速率和跳频带宽成正比。目前混合跳扩频通信系统的指标已经上升到了跳频速率每秒几万跳、跳频带宽几百兆赫的水平。由于系统跳频的驻留时间变短、带宽变大,且每个频点对应的误差不同,导致误差大范围快速跳变。使用传统反馈环路对误差进行补偿时,补偿速度往往跟不上误差变化的速度,导致环路失锁,同步失败。
针对上述问题,本文提出一种基于坐标旋转数字算法(Coordinate Rotation Digital Computer,CORDIC)的跟踪同步方法,在不改变系统内部其他信号的基础上同时对误差进行计算与补偿。此方法通过将系统误差映射到相位的方式,对多组误差进行二维旋转补偿,利用二进制相移键控(Binary Phase Shift Keying,BPSK)调制的性质,得到最佳旋转位和补偿误差。仿真分析表明,该方法在系统跳频速率20 000 hop/s、跳频带宽327.52 MHz的情况下完成了系统的跟踪同步,补偿性能相比于传统补偿技术具有明显优势。
1 系统结构
图1与表1分别为系统结构图、系统参数表。其中,信道编码采用卷积+RS级联码形式;扩频调制利用高速率伪随机码进行直接序列扩频;跳频调制分为IQ两路BPSK正交调制信号;DAC芯片用于产生中频载波,后经上变频发送。接收信号经下变频后通过ADC进行中频解调,利用参数与发射端相同的本地跳频载波和扩频码对信息进行捕获,捕获后的数据进行误差补偿实现跟踪同步,再经过信道译码还原信息。
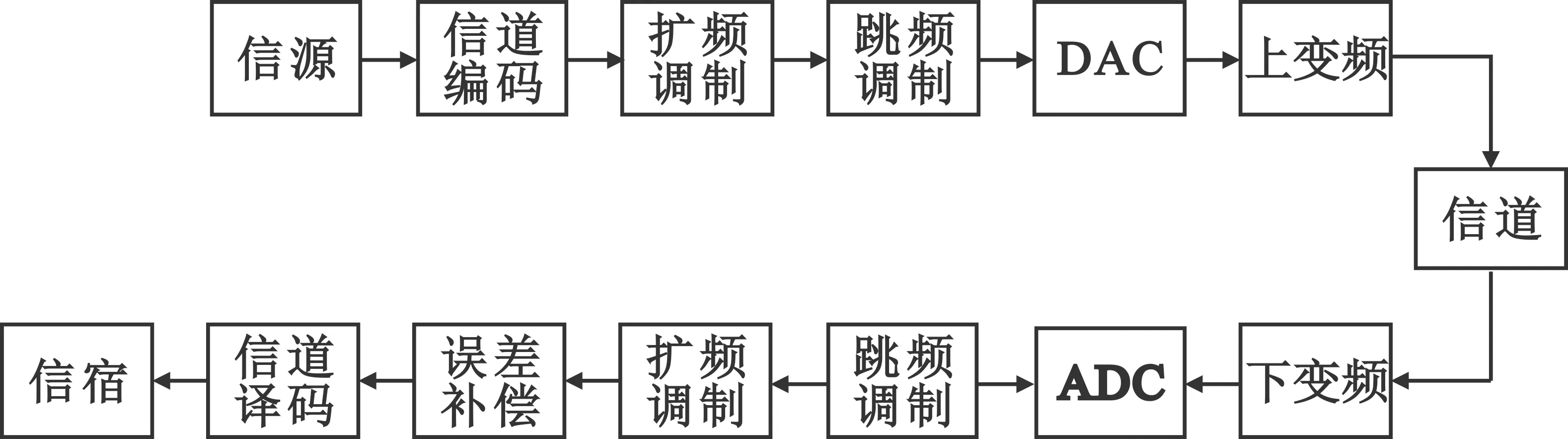
图1 系统结构图

表1 系统参数
2 系统误差分析
2.1 载波同步误差分析
载波同步误差可分为频率误差和相位误差两类。频率误差主要是因外界环境影响和系统上下行时钟不同源所致。外界环境产生频差最典型的就是多普勒频移,主要是相对运动所导致。相位误差是由于混频时载波的初相位不同而产生,而由于时钟不同源所导致的误差可以体现在很多方面。对于本系统,在信号经过下变频后进入ADC进行中频解调,此时由于时钟不同源,发射端和接收端所产生的中频载波之间会有一定的频率差值,所以在中频载波混频时会产生一个频率误差fmf。同样,在跳频解调中,双方的本地载波频率也会有差值,并且对应的每个跳频点的频率不一样其误差也会变化,这里统称这个误差为fhf。由于本系统跳频调制具有高跳速、多频点的特点,所以由此产生的误差也有着高动态、高随机性的特点,使用传统的反馈锁频环路方式对这种高动态误差进行补偿已经不太理想。
在系统的设计上,为了在跳频解调中减少不必要误差并保持载波相位的连续性,每个频点对应的跳频频率是跳速频率的整数倍。根据跳频速率fhs,可以得到频率误差进行累积的单位时间tf(单位:s)为
tf=1/fhs=1/20000。
(1)
根据基本的相位公式可以将频率误差映射为相位:
φ1=2π·Δf·tf=2π·(fmf+fhf)·1/20000。
(2)
式中:Δf为系统频率误差,在此状态下为中频混频误差fmf与跳频混频误差fhf的和。
2.2 定时同步误差分析
混合跳扩频通信系统中,时钟的不同源对于扩频部分来说会产生码偏,通过定时同步技术可以消除码偏。定时同步常用早迟门技术来对码偏进行补偿,实现对扩频码的跟踪。早迟门的原理是利用高频时钟对码片的不同位置进行采样,从而形成延迟路、信息路、超前路三路信号,通过反馈的信息对采样位置进行调整来接近最佳采样位。早迟门中能够调整的最大相位误差为扩频码片的一半[11]。
以本文系统为例,时钟频率为80 MHz,扩频码速率为10 MHz,码片采样精度为1/8。但在实际中这个采样精度并不能满足对最佳位置的捕获,误差可能为1/16、1/24、1/32个码片相位等更小的范围。当采样精度不能满足误差精度的时候,会出现采样位连续跳动的现象,随之会产生相位的跳动,严重时会造成误差浮动过大使系统失锁。由于对实际误差精度需求的未知,直接提高系统的采样频率来达到误差精度的做法既不现实又不灵活,还可能会对系统其他模块产生影响。所以,为了能在现有的条件下稳定高效地处理此误差,可以把对码片的相位采样当作时间上的采样,其中每个码片的时间就是其速率的倒数。而时间上的误差可以引起信号相位上的误差,将时间误差Δt映射为相位误差得到。
φ2=2π·fh·Δt。
(3)
式中:fh为每组跳频的频率。
3 基于CORDIC算法的相位补偿
3.1 CORDIC算法基本原理
CORDIC算法的基本思想是,通过加减和位移操作,利用与运算基数相关的一系列特定角度不断偏摆来逼近预设的旋转角度。如图2所示,将初始坐标P1=(x1,y1)点绕原点旋转θ角度后得到P2=(x2,y2)点。
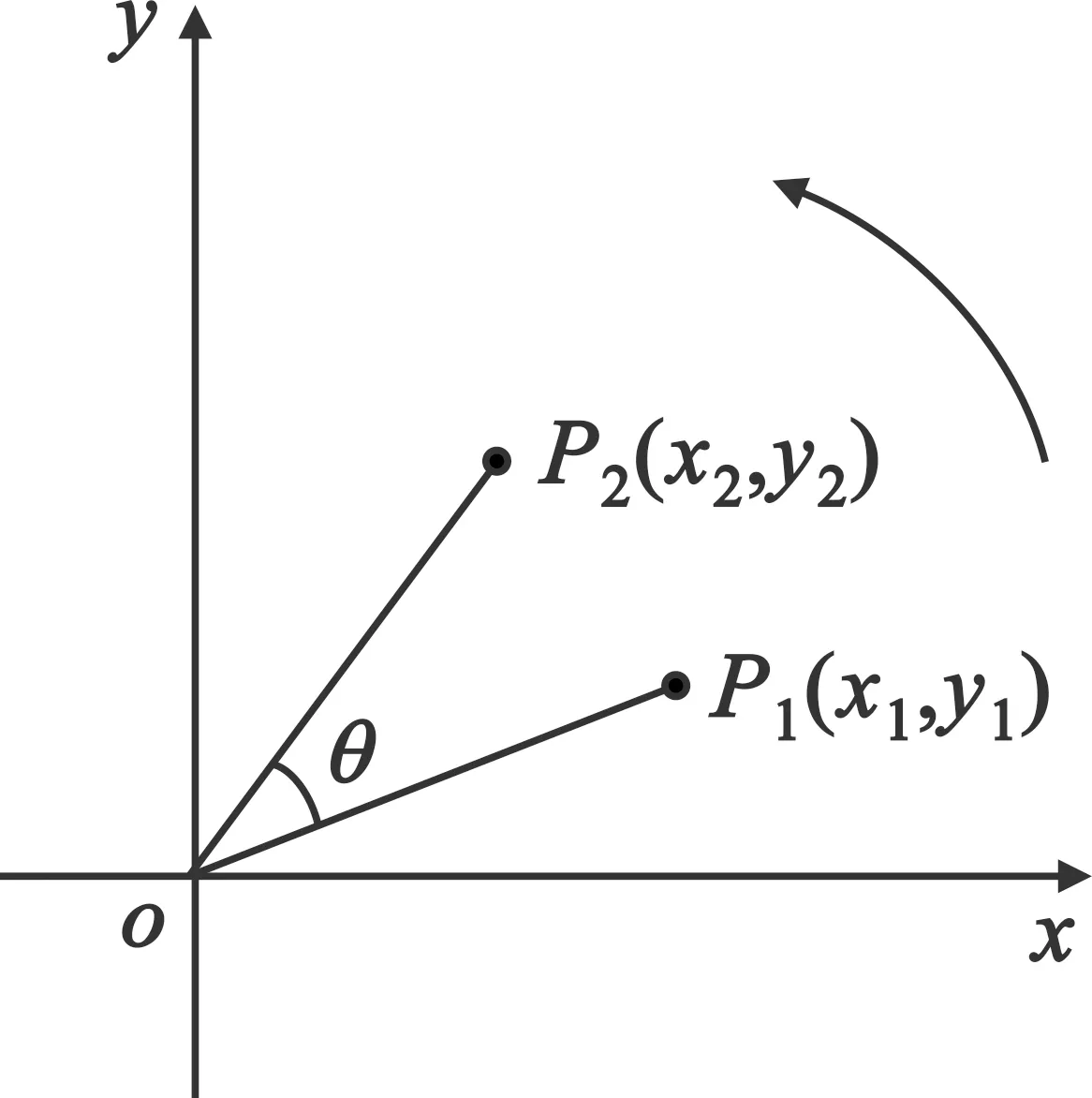
图2 CORDIC算法示意图
P2的坐标可以利用公式(4)计算:
(4)
3.2 补偿思路分析
在混合跳扩频信号误差补偿中,常用CORDIC的反正切算法计算出补偿角度和相位,将其反馈回本地载波发生器和伪码发生器上改变本地载波和本地伪码的频率或相位来达到同步目的[12]。
对于本系统而言,由于每个频点对应的误差角度和相位不同,误差存在多样化的特点。所以,在误差补偿的方式上并没有使用以往的CORDIC反正切算法,而是利用了CORDIC算法最基本的计算方法,即对信号的角度旋转或位移操作。上文中将分析出的误差都映射到了相位上,可以利用CORDIC算法对此进行补偿。
要通过CORDIC算法对数据进行旋转计算,就要确定旋转的范围,也是误差最大范围。通过之前的分析可以得到,接收端在对载波进行解调时产生的频率误差是以跳频速率的倒数作为单位时间的。根据公式(2)可得,当fmf+fhf取值为0~20 kHz时,φ1的取值范围为0~2π,对应到旋转坐标系中范围为一周;当fmf+fhf大于20 kHz时,由于旋转的周期性,计算出的相位映射到旋转坐标系中的范围仍然为0~2π,所以可以认为当Δf=fmf+fhf=20 kHz时频率误差最大。
对于系统扩频解调时采样引起的偏移误差,由于系统采用的是早迟门位同步环,采样相位最大误差为采样精度的一半,所以根据扩频码频率fs可以得到其对应的时间误差Δt的最大值Δtmax。
Δtmax=1/8·1/2·1/fs。
(5)
在这里假设系统上下行的时钟同源,即频率误差为零,以跳频带宽Δfbw为基准,代入公式(3),可以得到此时间误差引起的最大相位误差为
φ2=2π·Δfbw·Δtmax。
(6)
3.3 利用CORDIC算法的误差补偿
通过以上分析得到误差最大范围,可以在此范围内对数据进行旋转,达到补偿目的。由于两个误差是由不同的原因所产生,所以可以将此补偿过程看作是一个对系统的二维补偿。第一维补偿针对的是由载波解调引起的误差,相位中对应的时间单位为跳频速率fhs的倒数,以Δf=20 kHz为上限从Δf=0 kHz开始以40 Hz为步进计算相位,共分为500组,步进越小精度越高。第二维补偿针对的是早迟门引起的误差,对于公式(6)中的跳频带宽Δfbw,不同的频点对应着带宽中的不同频率,相对的误差也只是其中的一部分,并且各个频点之间有着相等的频率间隔,所以在保证精度的前提下将误差最大值平均分为n=256份,根据频点数ji每一份又平均分为2 048个点,得到步进Δε。将第一维相位误差Δφ1与第二维相位误差Δφ3相加得到一次步进旋转相位φ,以此为基础对信号进行扫描补偿。二维补偿相位公式如下:
(7)
(8)
φ=Δφ1+Δφ3。
(9)
补偿的信号是扩频解调后输出的IQ两路信号,其具有BPSK相干解调信号的性质,利用这个性质,进行多组信号一起补偿旋转,有助于找到最佳旋转位置,提取最佳补偿差。
将公式(9)的结果代入到公式(4)中,可以得到如公式(10)所示的旋转前IQ两路数据In和Qn与旋转后IQ两路数据In+1和Qn+1的关系:
(10)
式中:φ对应公式(4)中的θ,In、Qn与In+1、Qn+1分别对应x1、y1与x2、y2。
图3所示为具体的算法流程图,接下来将按照图中所示流程进行仿真分析。

图3 算法流程图
4 仿真与分析
为了验证理论分析结果,本文将对传统反馈环路补偿技术和本文提出的方法进行仿真分析和对比。文献[9]所提方法具有完整的混合跳扩频系统架构,且系统复杂度最低,补偿范围最大,系统性能较优;文献[10]所提算法对反馈环路进行了优化,可以使误差提取更加准确。因此,以表1所示的参数作为实验参数,通过Matlab工具对文献[9]中提出的方法和文献[10]提出的算法进行仿真对比。
以实际晶振误差1×10-6为参考,可计算出本文实验中80 MHz系统时钟的上下行时钟误差为80 Hz。在此状态下,利用文献[9]提出的方法补偿系统误差,得到图4所示补偿结果,通过鉴相器输出可以看出,当设置跳频频率不变时,反馈环路成功补偿系统误差实现跟踪同步;当跳频载波以20 000 hop/s的跳速进行跳变时,误差补偿失败。在此系统结构的基础上,利用文献[10]提出的算法进行仿真,得到图5所示结果。通过观察无跳频和跳频速率20 000 hop/s情况下的鉴相器输出结果可以看出,相比于文献[9]方法,在无跳频状态下,此算法提高了DDS相位差的收敛速度,但在跳频速率20 000 hop/s的情况下依旧不能成功补偿误差。因此,通过仿真分析可得,在面对高动态性误差时,基于反馈环路的补偿方法并不能满足具有此参数的混合跳扩频系统的设计需求。
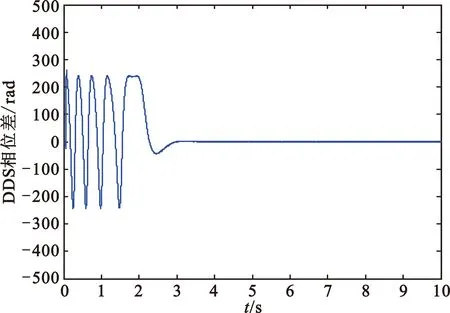
(a)无跳频情况下鉴相器输出

(a)无跳频情况下鉴相器输出
本系统以FPGA为基础平台,发射端与接收端采用不同源的两台设备,实验中使用的补偿数据为接收机现实接收数据,符合实际要求,实验具有真实性。图6为利用SignalTap工具采样得到的接收端扩频解调后的IQ两路实际数据,速率为20 kHz。其中,组合前的每一组IQ信号都代表着一个频点。为了便于得到最佳旋转位与补偿误差,需要将十组IQ数据组合成一组新的数据。
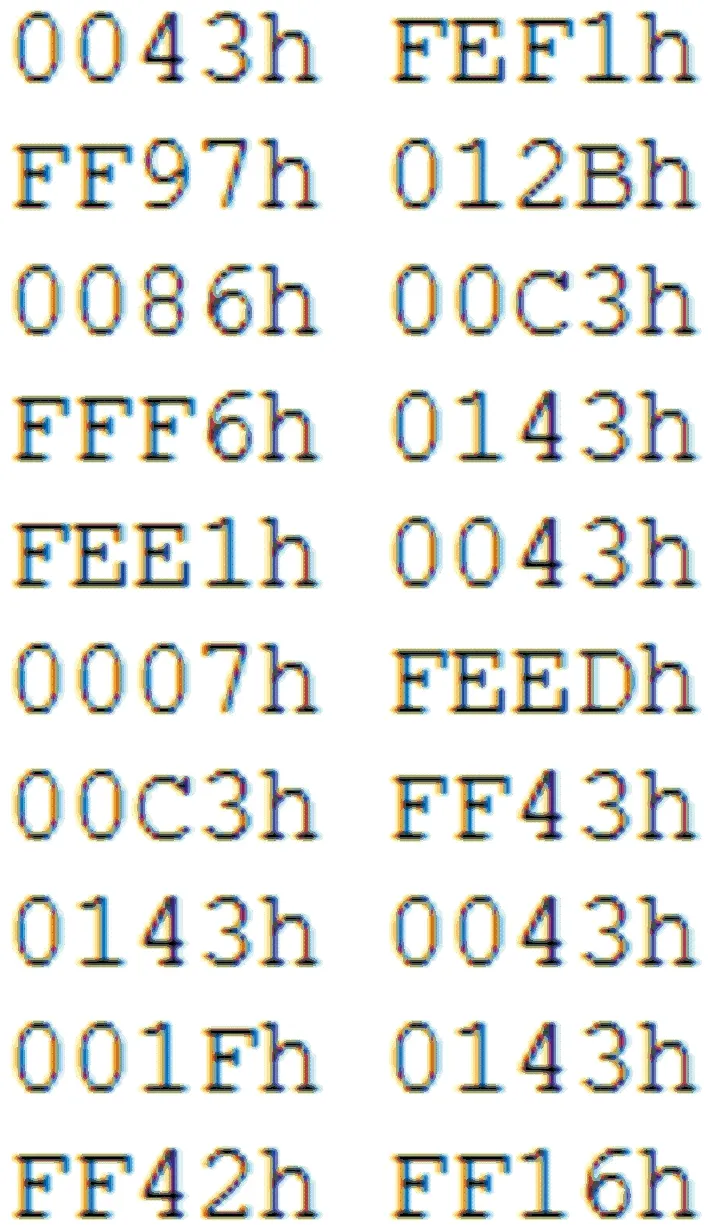
(a)组合前数据
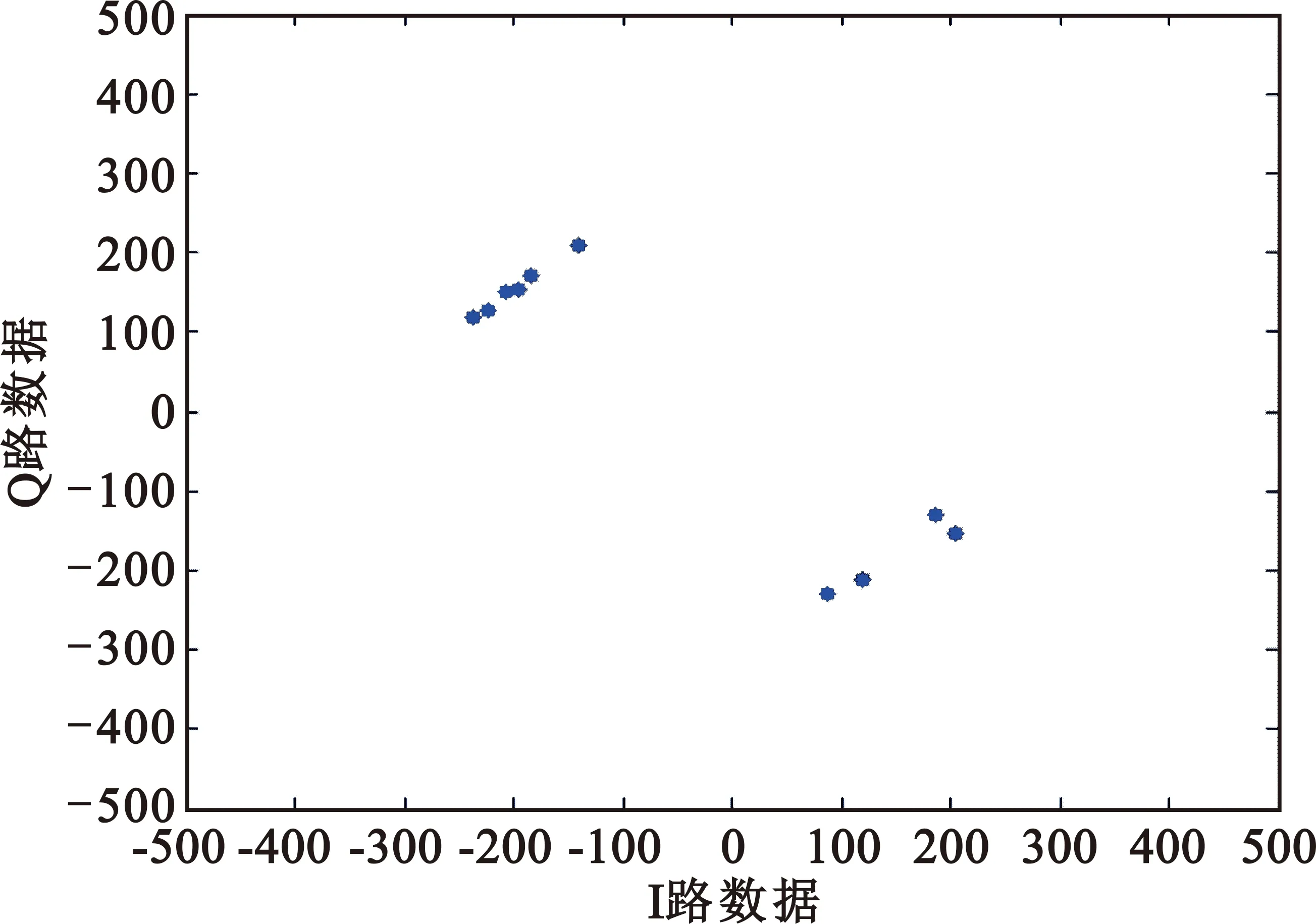
将数据导入Matlab做进一步分析,以I路数据为横坐标、Q路数据为纵坐标绘制星座图,如图7所示。可以看到这十组数据在星座图上的相对位置成散点状,说明系统中存在误差,并且每个频点对应的误差各不相同。

图7 无补偿状态下IQ数据星座图
根据公式(8)可知,每个点对应的旋转相位数值不同,在星座图上旋转速度也不一样,所以点间相对位置会发生变化。为了找出最佳补偿结果,每进行一次旋转就计算一次每个点与其他九个点的距离并求其总和。由BPSK解调性质可知,解调数据在星座图上的位置特点是成原点对称的,所以求得距离总和最小值即为符合其规律的最佳状态。旋转结果如图8所示,其中,点间距离曲线的数值对应着500组一维补偿中每组最小的二维补偿点间距离,取其中最小的一组,可以得到对应的m和n的值,代入到公式(7)和(8)中,可以计算得到最佳补偿相位,利用此相位数值进行旋转,得到旋转结果。可以看出,经过CORDIC算法计算的数据已经由散点转换为符合BPSK解调性质的图案,说明以上分析的误差已经被有效补偿。

(a) 点间距离曲线
将m和n的取值范围扩大一倍,即缩小第一维补偿与第二维补偿的步进后旋转,所得结果如图9所示。结合图8的点间距离曲线数据可以看出,与其结果相比,图9最小点间距离Y的值更小,聚拢程度更高,补偿误差的效果更好。所以,扩大m和n的取值范围,会提高补偿精确度,得到更好的补偿结果,但同时会增加计算时间,在实现方面会提升硬件资源的消耗量。所以,具体步进值需要根据系统设计要求与实验平台硬件资源情况来确定。
(a)点间距离曲线
由于在跳频解调时,上下行本地载波的初相不同,还存在一定的相位误差,所以再将此数据经过锁相环路后,得到如图10所示结果。可以看出Q路数值接近于0,误差被有效补偿,系统稳定同步。

图10 初相补偿后IQ数据星座图
为了防止误差波动,以此次旋转结果中m值对应的频率Δf为基准频率、左右取相邻频率作为调整频率进行旋转。比较旋转结果,取最小距离值所对应的m值和n值对信息进行计算,并将此次所取的m值对应的频率Δf设为新的基准频率,依此类推,从而保证系统的动态性能。
以本次试验参数为基础,可以得到表2所示的复杂度对比。由于本文采用扫描的方法对误差进行计算和补偿,计算的复杂度只与扫描范围和扫描步进有关,所以当扫描范围和扫描步进不变时,面对不同的系统参数,复杂度也是不变的。结合以上仿真分析可以看出,本文方法无论是在计算总量还是补偿性能上,都优于文献[9]和文献[10]所述方法。

表2 复杂度对比
5 结束语
本文提出了一种基于CORDIC的跟踪同步方法,在不影响系统内部其他信号的情况下可以完成对系统误差的计算与补偿。经过仿真分析,相比于现有文献提出的基于反馈环路的补偿方法,本文所述方法可以补偿跳速20 000 hop/s、带宽327.52 MHz的混合跳扩频通信系统误差,系统跳速更快、带宽更大。从算法复杂度和补偿性能的角度看,本文方法也具有明显优势。
本文只针对系统内部误差进行了分析,暂未分析多普勒频移等外界干扰。因此,下一阶段的工作是建立外部干扰实验模型,并进一步验证与分析算法性能。

