中温铯热管的启动及传热性能
郭宇翔,陈宏霞,袁达忠,李林涵,王逸然,纪阳
(1 华北电力大学能源动力与机械工程学院,北京 102206;2 中国科学院工程热物理研究所,北京 100190;3 中国科学院大学,北京 100049)
中高温热管是一种工作温度大于275℃[1]、工质为碱金属或其合金、壳体采用非透明耐高温材料[2]的高效换热器件,具有体积小、均温性好、传热性好等特点[3-4],被广泛应用于飞行器热防护、核反应堆散热、温度控制、余热回收等领域[5-8]。
目前中高温热管研究主要针对钠、钾碱金属工质[9-10]。Makhankov等[11]设计了高温钠热管用于聚变反应堆散热,其工作温度为500~1000℃。冯踏青等[12]验证了钠钾合金热管启动温度低于钠热管。Zeng等[13]优化了热管壁面外侧的翅片结构,开发出新型紧凑式高温翅片热管换热器。沈妍等[14]在热管内壁设置三角沟槽,强化工质在管内传输能力,提高了热管的热响应和热缓冲性能。
为具体描述强化热管的热性能,研究者开始关注热管的热启动过程及其均温性。热管的热启动过程是工质在蒸发段发生相变,流动至冷凝段再次进行相变换热的过程。Kemme[15]指出热管内部蒸气流动状况类似于拉伐尔喷管,对加热功率为6.4kW的钠热管进行变冷凝段工况试验,得到热管压力及温度梯度的变化规律。Dobran[16]指出声速极限受工作流体、蒸气流动面积以及绝热区长度的影响,并可能破坏热管表面。Wang 等[17]自主开发出热管瞬态分析程序,对带有保温情况的钾热管进行数值研究,得到不同时间热管速度分布,获得其声速极限规律。Wang 等[18]对钾热管启动特性进行了研究,在加热功率达到980W时热管发生声速极限。
针对热启动过程中工质流动状态的转折温度研究,Cao 等[19-20]建立了瞬态可压缩二维模型,提出两区模型,将热管划分为冷、热区;为热启动过程中确定转折温度奠定了理论基础。Tournier 等[21]对高温钠热管的冷态启动过程进行二维数值分析,建立三区模型。Ma等[22]发现高温钠热管“平面前锋”模型的对应温度在冷却对流换热系数h大于100W/(m2·K)时小于经典理论计算的转折温度,并建立纯导热瞬态模型进行验证。
对于热管均温性的研究,Teng等[23]开展了高温热管倾角α为0°、15°、30°、45°时的静态试验,考察了低频摆动对钠热管均温性的影响,观察到开始启动到稳定状态冷凝段和蒸发段温差变化不大。Zhao等[24]对比了重力和反重力情况对钠热管均温性的影响,在700℃工作温度下重力热管的最大温差为22.8℃,反重力热管最大温差为52.6℃,证明了反重力下该热管也具有良好的温度均匀性。Wang等[25]提出了一种利用钠钾合金热管的熔盐堆被动余热排出系统,对比了汽液界面、壁面、壁面毛细芯交界面均温性。张凯等[26]设计制备了一种重力型铯热管,证明了铯热管具有优异的均温特性和启动性能,可用于ITS-90国际温标锌凝固点复现。
由于铯工质化学性质活泼,中温热管制备难度大,很难制备出性能优异的热管,因此中温铯热管的研究较少[27],有关铯热管的蒸气工作温度、传热功率、均温性的研究报道有待进一步补充。同时,由于铯工质最佳品质因数对应温度与钠钾不同,且相比于钠钾热管,铯热管可在更低温度下成功启动。本文设计并制备了性能优越的铯热管,搭建了铯热管热性能试验台,对铯热管启动规律进行实验研究;测定中温铯热管的启动速度,定量测试热管发生声速极限的几何位置,为避免传热极限发生提供了参考。同时通过控制蒸发段热管吸热的热流密度,对不同加热情况下热管稳态的均温性作出对比,证明其均温性优异。
1 材料和方法
1.1 铯热管
铯热管壳体材料选取与铯具有相容性的不锈钢In600[28];工质为纯度98%的碱金属单质铯Cs,充装量为23.50g;吸液芯为双层高温合金丝网,孔隙率分别为400 目、100 目,丝径为0.1mm;热管全长240mm,直径φ为40mm,在热性能测试中,取蒸发段长度为70mm,冷凝段长度为170mm。为监测热管热启动到稳定过程中壁面的温度演变规律,沿热管长度方向x=30mm、55mm、75mm、100mm、240mm布置5个热电偶,具体结构尺寸及热电偶布置如图1。
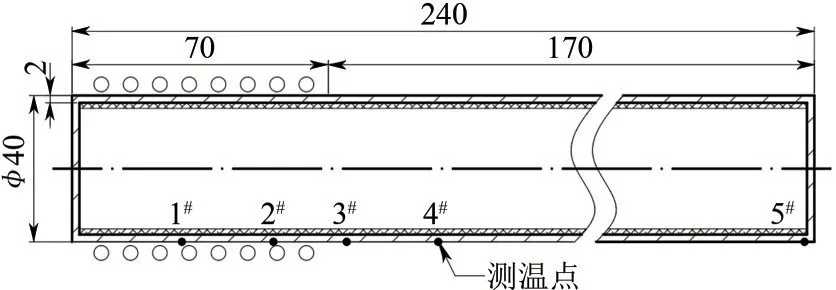
图1 高温热管结构尺寸及测试方法示意图(单位:mm)
1.2 实验测试平台
实验平台由热管加热系统及数据采集系统组成,如图2所示,加热系统主要由热管、高频感应加热器(XJH-20kW-A)、循环水冷却回路组成,热管倾角为90°垂直布置,蒸发段由高频加热器通过加热线圈提供热量,冷凝段的冷却方式为大空间自然对流和辐射散热,循环水通过中空的线圈可保证感应线圈温度不会过高;数据采集系统由数据采集仪(HIOKI-LR8431-30,精确度±0.80K,采集频率2s)并采用点焊机点焊接于铯热管壁面的多支K型热电偶(精确度±0.4%)构成。
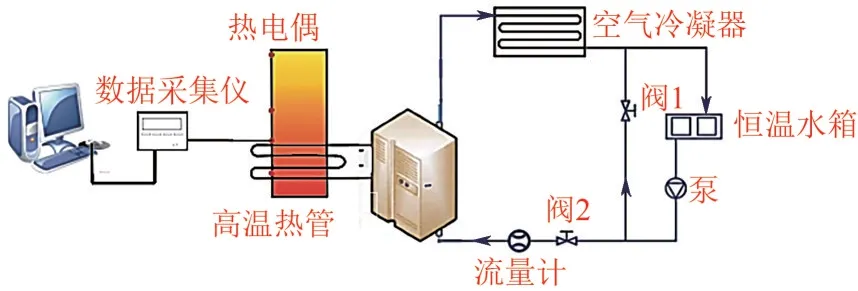
图2 高频电磁感应加热器加热系统
1.3 不确定性分析
本实验采用K型热电偶测量管壁壁温,所有位置均为单热电偶测温且热电偶最大允许误差为3.00K;热电偶测温的基本误差为1.73K;数据采集仪最大允许误差为0.80K,基本误差为0.46K;合成基本温度误差为1.79K。热管尺寸加工误差小于±0.5%。加热热流密度误差低于±6.5%,热阻误差小于±6.6%。
2 轴向传热功率计算
高频加热器在蒸发段的加热量假定全部经轴向传递到加热圈布置面积以外的热管段,基于对热管外端温度的测定以及换热理论模型获得加热圈外热管段的总换热量(热管热端吸热量)。加热圈外热管段的总热量可分为两部分:一部分是散热段与空气的自然对流换热;另一部分为散热段与空气的辐射散热。
铯热管壁面温度高于300℃时,辐射传热作用非常显著,辐射换热系数可通过式(1)计算。当铯热管在开敞空间内散热时,即φ12=1、εn=ε1,式(1)可变形为式(2)。
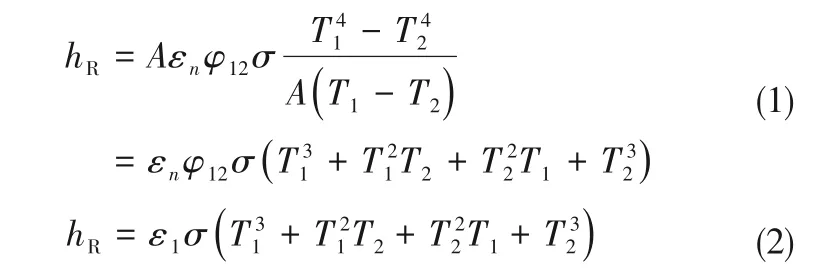
式中,T1为铯热管冷凝段壁面温度,K;T2为环境温度,K;ε1为壁面发射率;hR为辐射对流传热系数,W/(m2·K);σ为斯特藩-玻耳兹曼常数,σ=5.67×10-8W/(m2·K4)。
对于大空间竖直圆管壁面的自然对流传热的情况,设壁面温度为tw、环境温度(未受到壁面温度影响的流体温度)为t∞,空气假设为理想气体,热物性利用平均温度计算,定性温度为算术平均温度tm=0.5(tw+t∞)。大空间自然对流换热系数可由式(3)计算。

式中,hc为铯热管散热段壁面向环境散热的对流换热系数;λ为环境下空气的热导率,W/(m·K),需通过定性温度确定;l为散热段长度,m;NuD为由平均表面传热系数组成的Nu,由式(4)计算。
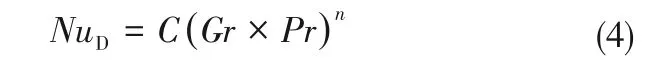
其中,Pr通过物性按定义式计算,格拉晓夫数Gr由式(5)计算得出。
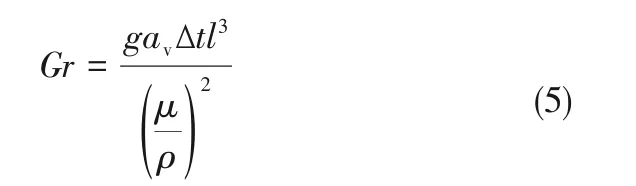
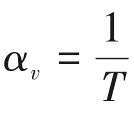
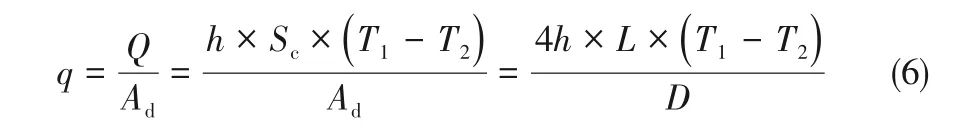
式中,Sc为热管传热器件侧壁面积;Ad为热管轴向横截面积;L为散热段长度;D为热管直径。
本实验中,L=190mm、D=40mm、T2=25.00℃,将不同高频加热器读数下热管冷凝段测定温度代入理论模型,可获得相应的轴向热流密度与高频加热器读数的关系,如表1所示。
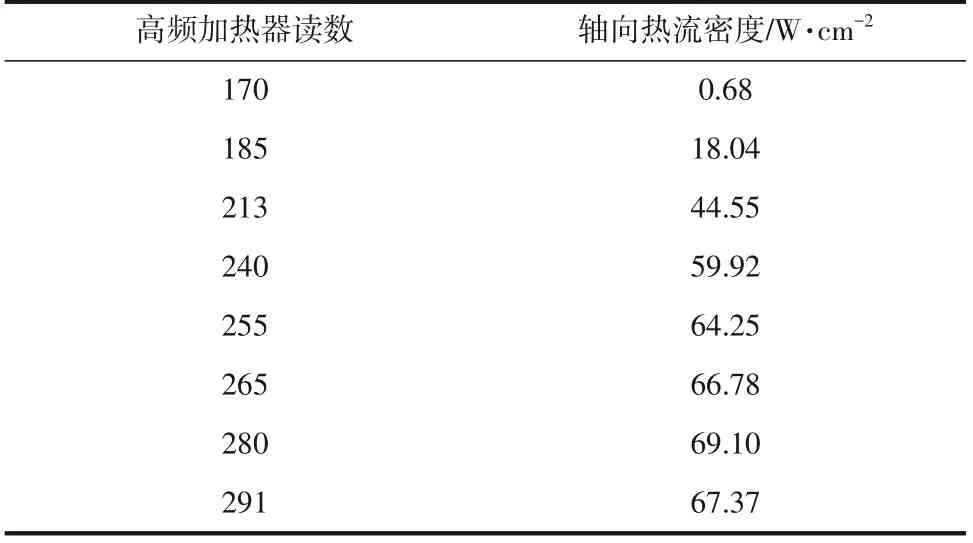
表1 通过传热模型不同高频加热器读数计算得到的轴向热流密度
3 结果与讨论
3.1 启动过程的温度演变规律
图3(a)为加热热流密度q=18.04W/cm2时铯热管的启动曲线,图3(b)为启动阶段轴向温度分布。热管蒸发段(x=55mm)、绝热段附近(x=75mm、x=100mm)以及顶端冷凝段末端(x=240mm)在热管启动伊始的温度均为室温。加热时间t=678s时热管蒸发段x=55mm位置处温度开始上升,稀薄蒸气流由蒸发段流向冷凝段,680s 时流至热管绝热段x=75mm 处引起温度上升,765s 时稀薄蒸气流至x=100mm 位置处,壁面温度开始升温。当加热时间t=840s,蒸发段x=55mm处温度上升至T≈332.30℃,脖颈位置x=75mm 与x=100mm 处温度曲线基本重合,温度T≈279.90℃;位于蒸发段和绝热段的3个测温点升温速率均变缓;蒸气未流至冷凝段末端,x=240mm处温度未上升。t=870s后蒸发段蒸气开始由稀薄蒸气流转变为连续蒸气流并流向冷凝段,自由分子流到达x=240mm 处并引起该处温度缓慢上升。在t=1159s 前,热管蒸发段一直处于最高温,中间绝热段居中,冷凝段温度最低,热管尚未完全启动;从t=1159s开始连续蒸气流到达冷凝段末端,热管冷凝段末端温升变缓且与热管底部、颈部处温度接近。随后冷凝段末端温度逐渐接近蒸发段温度,由于到达声速极限,冷凝段温度反超绝热段温度。到t=2400s 后热管各测温点的温度趋于稳定,且热管蒸发段及冷凝端末端稳定温度Ts分别为543.50℃、542.40℃。由图3中数据可知,启动过程中蒸发段温度未出现远超过绝热段温度的情况,可知铯蒸气在冷凝后可及时回流至蒸发段。
对比不同位置热电偶温度,热管冷凝段末端x=240mm处温度与蒸发段温度相差1.10℃左右;内部连续分子态蒸气流由蒸发段喷射入冷凝段,其流场分布同拉伐尔喷管,热蒸气在蒸发段出口处流速达到最大,相应压力降到最小,造成壁面温度下降。如图3(b)所示,蒸发段出口温度开始降低,在绝热段x=75mm处温度降到最低,之后温度回升且略低于蒸发段温度;绝热段最低温度与蒸发段温度相差30.00℃,证明热管达到了声速极限[15]。
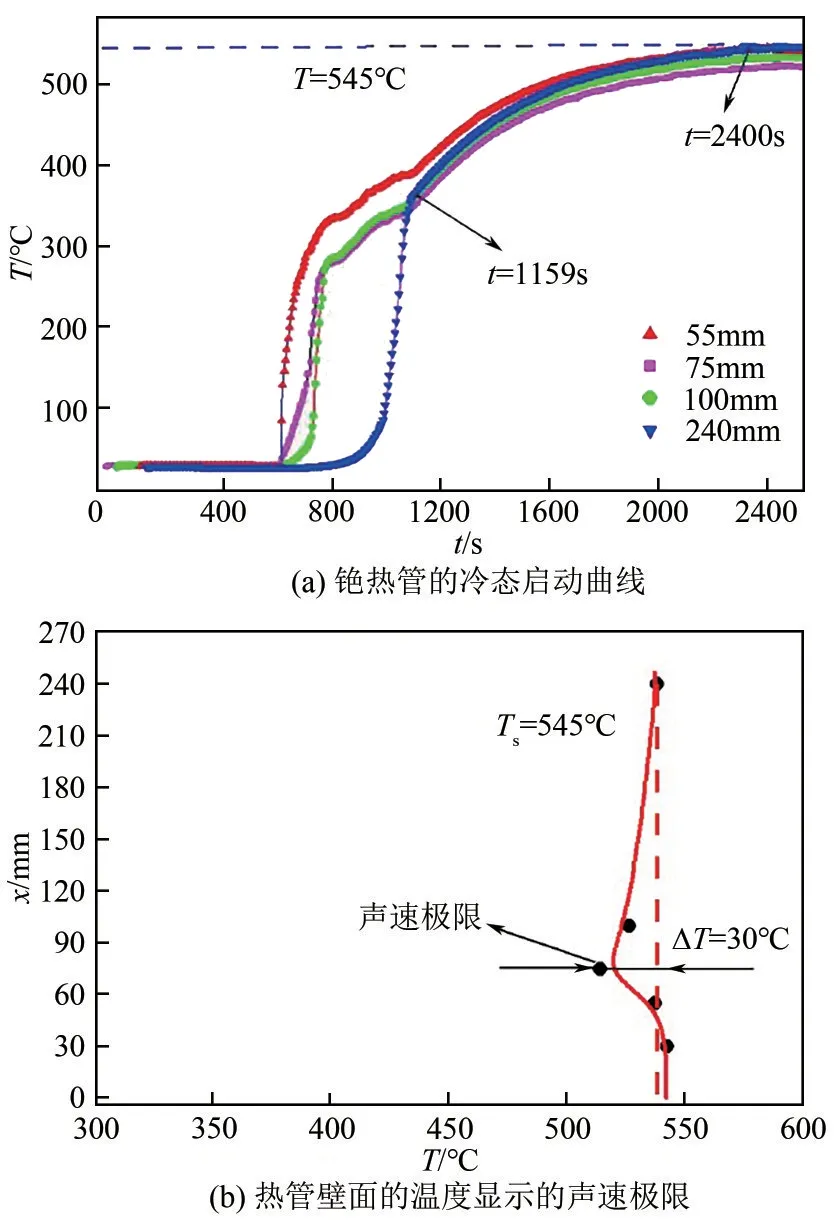
图3 热管启动曲线
由上述启动过程可知,到达转折温度后铯工质由自由分子流转变为连续蒸气流状态,蒸发段的热量传递到冷区,冷区开始快速升温,热区升温速度开始减缓;经过一段时间后热管蒸发段、绝热段以及冷凝段的升温速度基本一致,直到热管完全启动,实现热管冷凝段温度与蒸发段温度基本相等。铯热管的冷启动特性与钠热管相似。
3.2 启动转折温度值
利用量纲为1 的Knussen 数(Kn)建立分子平均自由程λ与热管管径D之间的关系,并利用Kn判断热管内铯工质的状态。

通常认为,当Kn>1.0 时,蒸气为自由分子流状态;当0.01<Kn<1.0 时,蒸气为从自由分子流向连续流转变的中间过渡状态;当Kn<0.01时,热管内蒸气为连续流动状态;当Kn=1.0 时,蒸气开始从自由分子流向中间过渡状态转变;当Kn=0.01时,蒸气由过渡状态向连续流动状态转变[19]。不考虑分子间的引力,认为铯蒸气分子为刚性小颗粒且直径为σv,则其分子平均自由程根据Maxwell 理论推导如式(8)。
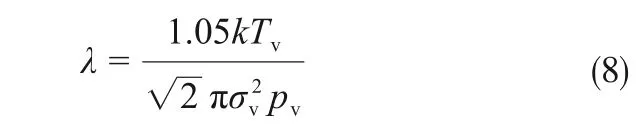
式 中,k为Boltzmann 常 数,k=1.3806505×10-23J/K;Tv为当地蒸气温度;Pv为Tv对应的蒸气压力;其中铯的有效分子直径σy=5.20×10-10m。当蒸气达到饱和,且温度达到转折温度,联立式(7)及式(8)获得对应于Kn下热管直径D和转折温度Ttr的关系式,如式(9)。单质Cs 的饱和蒸气压与饱和温度的关系曲线[29]如式(10)。
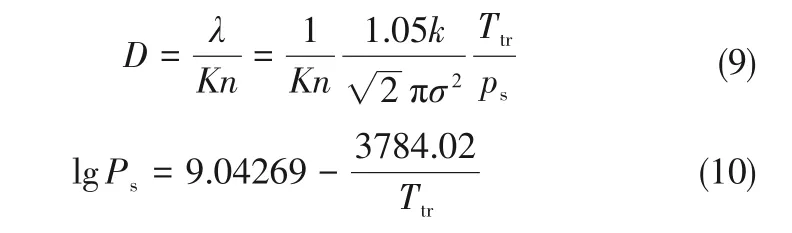
式中,Ps为对应于Ttr的蒸气饱和压力。
联合式(9)与式(10),求解铯热管冷启动过程中由初始过程蒸发器为自由分子态到中间过渡态的转折温度Ttr1(Kn=1.0)以及过渡态到连续态的转折温度Ttr2(Kn=0.01);获得转折温度为Ttr1=107.70℃、Ttr2=209.95℃。如图4 实验数据可知,铯热管的转折温度约为200.00℃,与Ttr2计算值误差较小,因此认为铯热管启动时的转折温度模型与钠热管相同,但利用Kn=0.01 获得Ttr2与实验测量值更为接近。
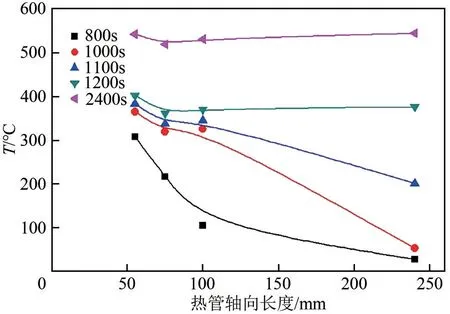
图4 轴向温度演变规律
3.3 冷凝段不同换热方式对铯热管启动规律影响
图5为加遮热罩保温与大空间自然对流不保温启动温度演变过程的比较,以蒸发段x=55mm处热电偶开始升温为基准,假定此时刻t=0s。选取x=100mm 和x=240mm 两处测温。由图5 可知不保温及保温时达到稳定升温状态的温度分别为350.00℃及350.50℃,即换热方式对铯热管启动过程达到稳定升温状态的温度几乎没有影响,主要与热管工质本身物性有关。但散热方式对启动时间影响明显,如图5(b),不保温时热管达到稳定升温状态的时间比保温情况下长;外加遮热罩情况下达到稳定升温状态的时间为404s,自然对流情况下则需472s。外加遮热罩时热管径向热损失小,大部分高频加热器热量用于加热铯工质并沿热管轴向传至冷凝段;不保温时损失掉一部分高频加热器产生的总热量,使得工质转变时刻更晚,热管达到的稳定工作温度Ts较低。此外,自然对流启动过程中温度上升,曲线斜率较低甚至略有波动,也是由于环境散热及波动引起的。总体而言,不同散热情况对启动时间影响较大,对热管转折温度几乎无影响,同时可利用外置遮热罩加快热管稳定速度。
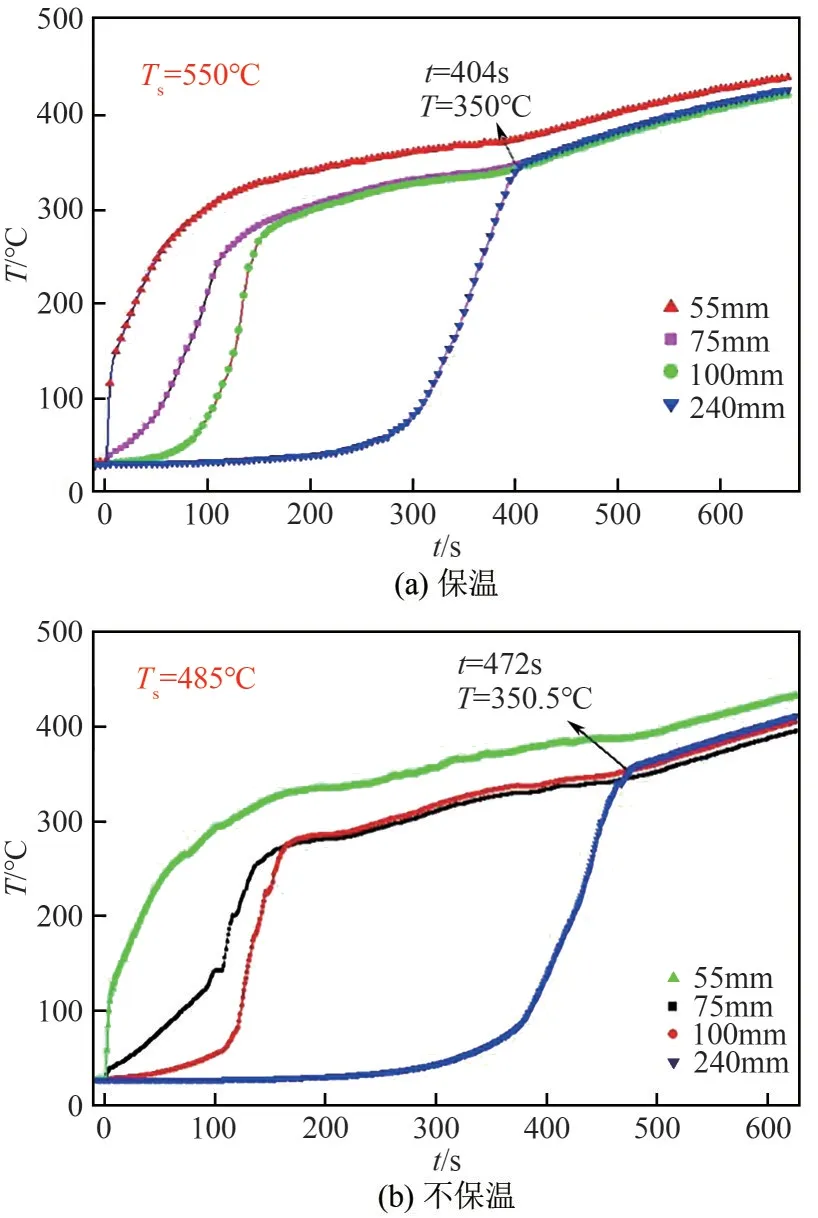
图5 相同加热功率、不同环境下铯热管的启动温度(q=18.04W/cm2)
3.4 不同热功率对铯热管稳定温度的影响
图6(a)为不保温情况下改变加热功率对铯热管稳定工作温度Ts的影响曲线。如图所示,在加热功率q=44.55W/cm2时开始冷态启动,热管达到稳定时工作温度为505.00℃(t=800s)。然后每800s 增加加热功率,相应加热功率依次为59.92W/cm2、64.25W/cm2、66.78W/cm2。热管在较高功率下均能够在800s 内达到稳定,随功率增加获得相应稳定温度依次为551.00℃、569.00℃、582.00℃。同时可知,在加热功率每次增加时,各测点温度同时稳步上升,保持了良好的均温特征。统计不同加热功率下的稳定温度并与保温条件下的稳定温度进行比较可知,由于热损失的存在,相同加热功率下保温热管稳定温度高于不保温热管的稳定温度[图6(b)];随着加热功率的增大,热管稳定温度增大,且保温情况下热管稳定温度变化曲线为下凹曲线的右侧,不保温情况下热管稳定温度曲线为上凸曲线的左侧,即伴随加热功率的增大,保温热管温度升高速度加快,而不保温热管温度升高速度减慢,热损失随加热功率增大而增大。
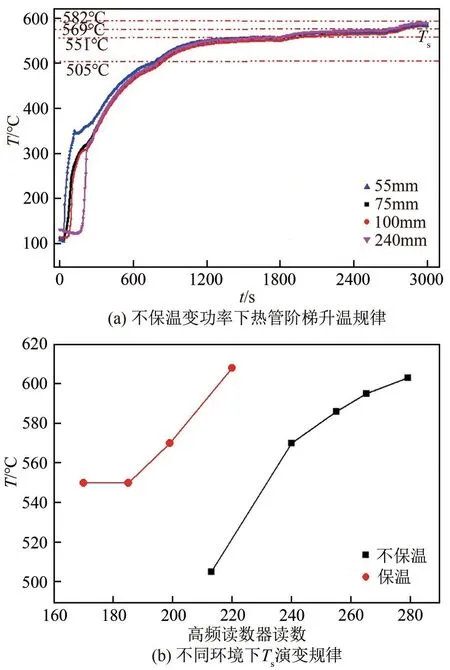
图6 加热功率对热管稳定温度的影响
3.5 铯热管均温性
图7(a)为不保温情况下热管各位置处温度,热管在蒸发器底部温度最高;由于轴向热流密度不同,内部工质的流速及流态不同,工质在蒸发段经过不同距离后液相转变为汽相,在蒸发段出口处铯蒸气达到超声速,在绝热段气相主要聚集于管道中心使得管壁温度下降;经过绝热段后汽相工质进入冷凝段使得热管壁面温度开始回升。加热功率达到64.25W/cm2、稳定温度达到569.00℃时,伴随蒸发段加热功率增大,热管管壁向空间的散热损失增大,冷凝段顶部温度Tc和蒸发段底部Te的温差ΔTe-c亦略微增大,冷凝段最顶端温度与绝热段最低温度的差ΔTc-min均不大于7.00℃,且伴随加热功率的增大相对稳定,整个冷凝段热管具有良好的均温性及传热性能,其有效长度为100%。
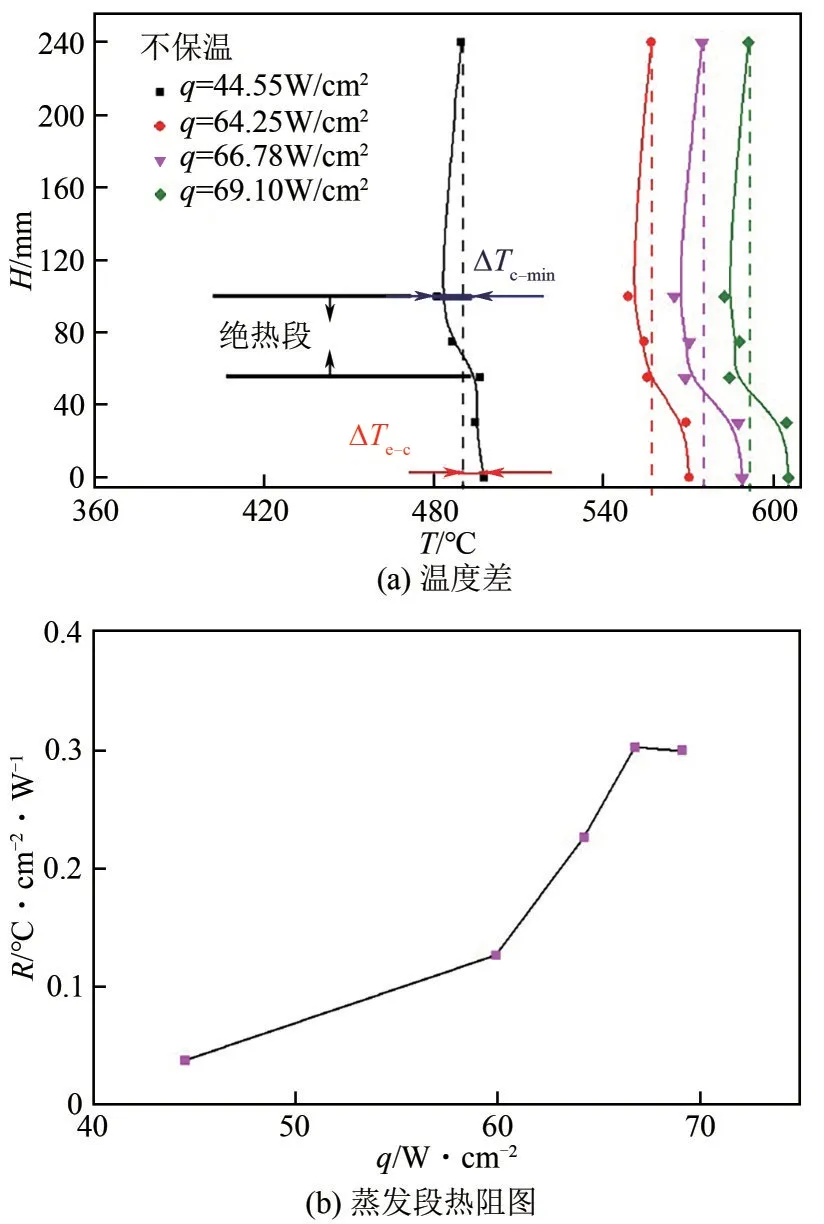
图7 散热情况下热管各位置温度及蒸发段热阻随加热功率的变化规律
由图7(b)可知,q=64.25W/cm2时蒸发段热阻显著增大,高温铯热管蒸发段加热面出现携带极限及毛细极限。部分工质相变后以汽相或以壁面液膜的形式存在于冷凝段,回流至蒸发段液量减少,继续增大加热功率时蒸发段无足够的工质吸收热量进而引起壁面干烧;达到此临界值时,由于蒸发段壁面温度上升,相应引起ΔTe-c的增大及热管均温性的衰退。
4 结论
本文设计并制备了性能优异、直径为40mm、长度为240mm 的中温铯热管,定量考察了在不同加热功率及散热情况下,冷态启动过程的转折温度、达到稳定传热时的工作温度及均温性的影响规律,得到以下结论。
(1)铯热管具有较快的启动速度,加热热流密度q=18.04W/cm2,启动时间为1750s;同时,铯热管展示了较好的均温特性,各加热功率下冷凝段最顶端温度与绝热段最低温度的差ΔTc-min均不大于7.00℃,且最大温差随加热功率增加波动较小。
(2)基于实验转折温度的数据可知,铯热管启动与钠热管原理相似,利用Kn=0.01计算转折温度与实验数据更接近。
(3)在自然对流不保温换热情况下,热管达到稳定状态后,随着加热功率的提高,铯热管仍保持良好的均温性;稳定温度随加热功率增大而升高,且呈现“凹”字形。带遮热罩的保温情况下,铯热管稳定温度随加热功率增大曲线呈现“凸”字形,相对自然对流换热而言,相同加热功率下其稳定温度更高,且升温速度更快。

