不同类型储层物性关系研究
刘雄,严乐,范鑫,张洋
不同类型储层物性关系研究
刘雄1,2,严乐1,范鑫1,张洋1
(1. 西安石油大学 石油工程学院, 陕西 西安 710065; 2. 陕西省油气田特种增产技术重点实验室, 陕西 西安 710065)
基于大庆油田179块岩芯实验数据,对储层渗透率分类,探讨了不同分类条件下渗透率、孔隙度、中值半径、束缚水饱和度之间的关系,并给出了渗透率与孔隙度的最优拟合关系式,同时结合岩心扫描电镜及实验数据分析了孔隙度、中值半径、束缚水饱和度与渗透率的相关性。结果表明:基于渗透率分类能在一定程度上提高孔隙度与渗透率拟合精度;大于100 mD的岩芯,与渗透率相关性从大到小排列有:中值半径50、束缚水饱和度S、孔隙度,其中中值半径是主控因数,其平方值与渗透率有最佳的线性相关性;对于渗透率小于20 mD的岩芯,与渗透率相关性有:束缚水饱和度S>孔隙度>中值半径50,当渗透率小到一定值时,喉道对流体渗流影响被削弱,而孔隙的影响会增大;对于渗透率在20~100 mD之间的岩芯,束缚水饱和度、中值半径与渗透率相关性最差,拟合孔-渗关系式建议采用幂指数函数。
渗透率;孔隙度;中值半径;束缚水饱和度;岩芯实验;扫描电镜
渗透率和孔隙度都是储层描述的基本参数。在油田开发很长一段的时间里,储层渗透率只能通过复杂岩芯实验或试井解释来获取,G. E. Archie基于资料分析给出了孔隙度和测井数据的经验关系式[1-2],这使得利用测井资料计算储层渗透率成为可能,国内外很多学者基于理论推导、等效实验等方法对某些特定区块的孔隙度和渗透率关系做了大量研究[3-11],得到了不少孔隙度与渗透率的相关式。一方面,截至目前没有文献规范这些关系式的适用范围,另一方面,由于影响孔-渗关系式的因素很多,使用单一拟合公式描述同一区块所有岩芯的孔-渗关系,其计算精度远无法满足工业需求。基于不同喉道分类,学者王永兴[12]分析了大庆油田高孔高渗砂岩岩芯的孔-渗关系;在C.Ergun[13]及Bear[14]研究基础上,结合实验结果,雷树业[15]给出了不同颗粒等值粒径分类下孔隙度与渗透率关系式;T.Torskaya[16]基于Wullie-Rose[17]的研究成果,分析了束缚水均匀以及非均匀吸附下不同岩芯的孔渗关系式并校正了拟合系数。
本文以大庆油田实际岩芯测试数据为基础,探究不同渗透率分类下大庆油田适用的孔-渗关系表达式,分析对比了各个因素对孔-渗关系式影响的敏感程度,为大庆油田基础数据研究及应用提供一定依据。
1 孔-渗经验关系式对比
相同的孔隙度对应的渗透率很可能存在差异,造成这种情况的因素很多,只有引入其他主控影响参数才能建立高精度孔-渗关系式。目前,应用较为广泛主控参数有中值半径、束缚水饱和度以及岩石颗粒平均直径。
1.1 Carman-Kozeny[18]公式
基于圆管层流模型,考虑了岩石孔隙结构影响,推导出了孔-渗关系式:

式中:—岩石渗透率,10-3μ32;
—岩石孔隙度,%;
0—喉道半径,μ道2;
—迂曲度,表示孔道迂曲程度,一般取值1.5~5.5。
式(1)不考虑启动压力梯度及压敏影响,式中迂曲度值以及等效喉道半径都不易获取,本文对式(1)做了修正,修正后公式为:

式中:500喉道中值半径,可通过压汞实验获取,μ道2;
—常数,无因次。
1.2 Timur[19]公式
Timur总结了孔-渗之间的关系表达式:

式中:S—束缚水饱和度,%。
Timur公式是个经验公式,一般认为束缚水均匀分布,束缚水饱和度与岩石比面成正相关。后来学者Tixier[20],Coates[21]以及T.Torskaya[16]都对该公式做了修正以适用不同区块的储层预测,Tixier、T.Torskaya修正公式可归纳为:

式中:、、—常数项,无因次。
Coates公式:

2 岩芯数据分析
本文实验数据来自大庆油田12个区块10个油层组共179块岩芯,孔隙度分布在0.123~0.336之间;渗透率分布范围0.2~8 230 mD。
通过岩芯实验数据做了拟合发现,式(2)整体拟合程度最好,可以看出:关系式拟合结果对大于100 mD岩芯的计算误差较小,而对小于100 mD的岩芯计算误差偏大,且岩芯渗透率越小,拟合相对误差越大。本文以20 mD和100 mD作为渗透率分类界线,分别对岩芯数据进行分析研究(这里将20 mD也作为一个分类标准,会在后续数据分析中给予说明)。
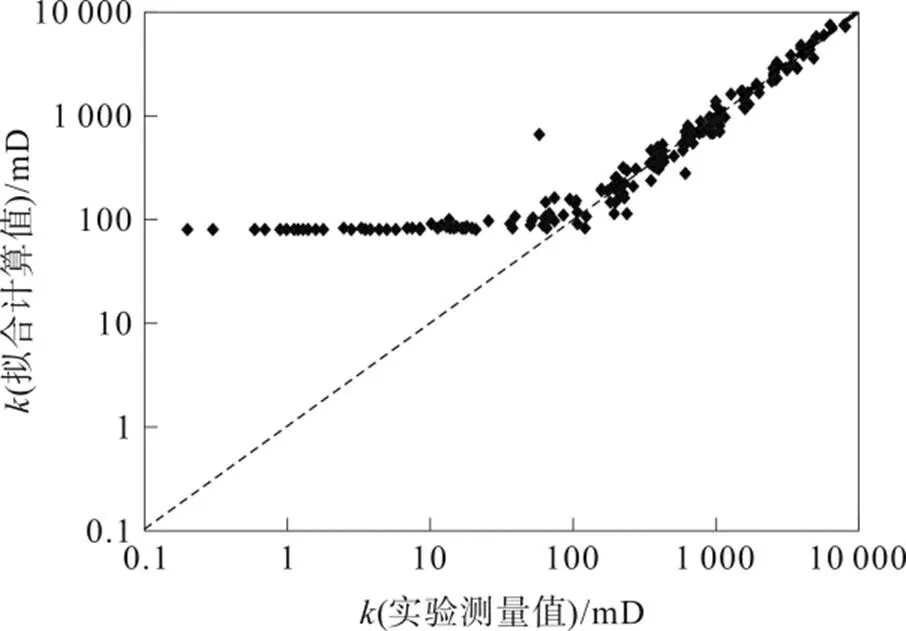
图1 渗透率实际测量值与拟合计算值对比
2.1 大于100 mD岩芯数据分析
由表1可看出式(2)有最好的拟合度,其他关系式的拟合程度都非常差,该范围内孔隙度与渗透率关系满足:
= 0.417 1502(8)
该拟合关系式有较好的相关性(见图2),判定系数2=0.961 9,所有拟合计算值与实验测量值相对误差控制在20%以内。
从公式(3)和公式(4)的拟合结果来看,对于大于100 mD岩芯,孔隙度与渗透率的相关性要略大于束缚水饱和度与渗透率的相关性。

图2 大于100 mD岩芯孔隙度、中值半径与渗透率关系图
2.2 小于100 mD岩芯数据分析
从表2中可以看出,式(4)有最好的拟合度,判定系数2=0.816 6,拟合相对误差小于65%,该范围内孔隙度与渗透率关系满足:

图3是公式(4)拟合小于100 mD岩心的幂指函数拟合关系式及参数。
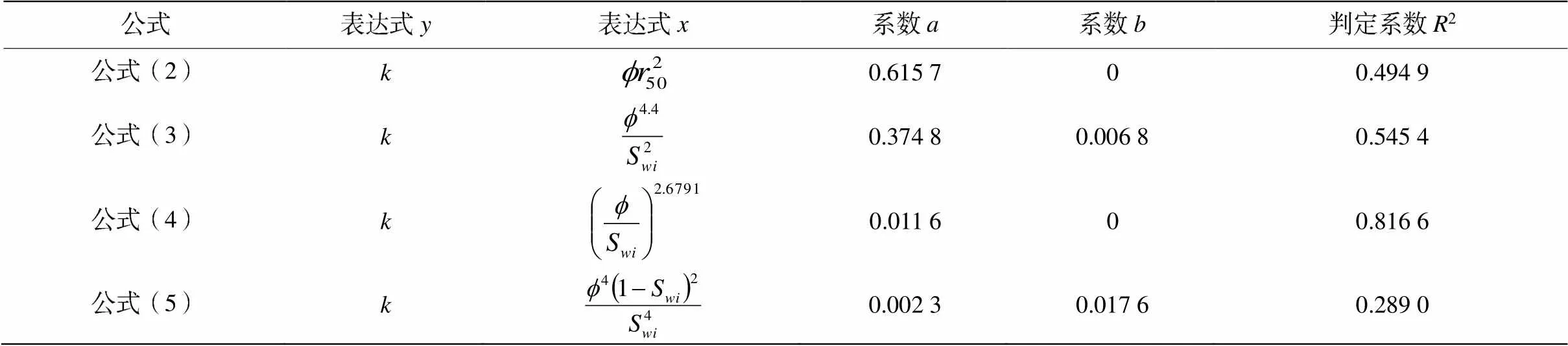
表2 小于100 mD岩芯孔-渗关系式拟合参数表(通式:y=ax+b)

图3 小于100 mD岩芯孔隙度、束缚水饱和度与渗透率关系图
从图中可以看出大于20 mD实测数据较为发散,而低于20 mD实测数据拟合相关性较强,因此20 mD可以作为一个区分不同主控因素的分界线。
3 因素相关性分析
图4展示了不同渗透率岩芯扫描电镜图片。

图4 不同渗透率岩芯扫描电镜图
对比图片可以看出:随着储层渗透率从0.053 mD增大到1 524 mD,岩芯颗粒直径也从几十微米增大到2 000 μm左右。
表3展示了不同渗透率分类下,中值半径、孔隙度、束缚水饱和度与孔隙度的相关系数。可以看出中值半径、孔隙度与渗透率成正相关,束缚水饱和度与渗透率呈负相关。
对于渗透率大于100 mD岩芯,与渗透率相关性:中值半径50>束缚水饱和度S>孔隙度,且中值半径是主控因素,这类储层可用圆管模型来替代模拟实际流体渗流过程;对于渗透率小于20mD岩芯,与渗透率相关性有:束缚水饱和度S>孔隙度>中值半径50,这是因为随着渗透率降低,喉道对流体流动的影响会被削弱,而孔隙对流体流动影响会增大;对于渗透率在20 mD到100 mD之间的岩芯,喉道没有100 mD以上岩芯具备明显绝对优势,也不像20 mD以下岩芯一样分布较为平均,使得其与渗透率相关性是所有分类中最差的,这个范围内的渗透率,需要同时纳入中值半径与束缚水饱和度两个因素的影响。

表3 各个因素与渗透率相关性系数表
4 结 论
1)基于大庆油田实际岩芯实验数据,对储层渗透率分类,并给出不同分类下渗透率与孔隙度的最优拟合关系式,大于100 mD岩芯拟合相对误差小于20%,小于100 mD岩芯拟合相对误差小于65%。
2)对于渗透率大于100 mD岩芯,与渗透率相关性从大到小排列:中值半径50、束缚水饱和度S、孔隙度。中值半径是主控因素,其平方值与渗透率有最佳的线性相关性。
3)对于渗透率小于20 mD岩芯,与渗透率相关性有:束缚水饱和度S>孔隙度>中值半径50,当渗透率减小时,孔喉对流体渗流影响被削弱,而孔隙的影响会增大,这时与比表面相关的束缚水饱和度、孔隙度对渗透率的影响要大于中值半径。
4)对于渗透率在20 mD到100 mD之间的岩芯,中值半径、束缚水饱和度与渗透率的相关性是所有分类中最差的,这个范围内孔-渗关系需要同时考虑中值半径与束缚水饱和度的影响。
[1] 赵桂青. 东辛油田营86-87区块沉积微相与储层物性关系研究[J]. 内蒙古石油化工,2010,36(11):130-131.
[2] 孙建国.阿尔奇公式:提出背景与早期争论[J].地球物理学进展,2007,22(2):472- 485.
[3] 邵维志,解经宇,迟秀荣,等.低孔隙度低渗透率岩石孔隙度与渗透率关系研究[J].测井技术,2013,37(2):149- 153.
[4] 张顺存,王凌,石新璞,等. 准噶尔盆地腹部陆西地区石炭系火山岩储层的物性特征及其与电性的关系[J]. 天然气地球科学,2008,19(2):198-203.
[5] 李留仁,袁士义,胡永乐,等.分形多孔介质渗透率与孔隙度理论关系模式[J].西安石油大学学报(自然科学版),2010,25(3):49-52.
[6] 陈晓林,于炳松,刘忠宝,等. 库车前陆盆地克拉2气田白垩纪基准面旋回与储层物性的关系[J]. 新疆地质,2006,24(2):176-181.
[7] 杨帆,王鹏,朱建安,等. 鄂尔多斯盆地集义地区山西组砂岩储层孔隙结构特征及其与物性的关系[J]. 地下水,2017,39(3):183-186.
[8] 徐文明,蒋启贵,刘伟新,等. 江汉盆地潜江凹陷盐间潜34油组储层微观结构特征及与物性的关系[J]. 石油实验地质,2020,42(4):565-574.
[9] 范小军,黄勇,厚东琳,等. 储层物性与产能的关系——以元坝长兴组礁滩相储层为例[J]. 天然气技术与经济,2011,5(4):29-32.
[10] 余明发,林秋野,王勇,等. 东濮凹陷砂岩储集层物性参数关系研究及随钻应用方法[J]. 录井工程,2006,17(1):32-35.
[11] 周晓亭,阴静慧,刘航,等. 准东地区煤储层物性与煤层气可采性关系研究[J]. 煤炭技术,2014,33(8):244-246.
[12] 王永兴,刘玉洁,卢宏,等.高孔隙度砂岩储层中砂体成因类型、孔隙结构与渗透率的关系[J].大庆石油学院学报,1997,21(1):12-16.
[13] ERGUN S. Fluid flow through packed columns[J]., 1952,48:89-94.
[14] BEAR J. Dynamics o fluids in Porous Media[M]. USA: American Elsevier Publishing Company, 1972:129.
[15] 雷树业,王利群,贾兰庆,等.颗粒床孔隙率与渗透率的关系[J].清华大学学报,1998,38(5):76-79.
[16] 唐海发,赵彦超,汪立君. 胜坨气田明化镇组下段沉积微相特征及其与储层物性的关系[J]. 天然气地球科学,2004,15(3):257-260.
[17] WYLLIE M R J, ROSE W D. Some theoretical considerations related to the quantitative evaluation of the physical charateristics of reservoir rock from electrical log data[J]., 1950, 189: 105.
[18] 秦积瞬, 李爱芬. 油层物理学[M]. 中国石油大学出版社, 2006.
[19] TIMUR A. An investigation of permeability, porosity, and residual water saturation relationship for sandstone reservoirs[J]., 1968, 9 (4):8-17.
[20] 陈继华,陈政,毛志强. 低孔隙度低渗透率储层物性参数与胶结指数关系研究[J]. 测井技术,2011,35(3):238-242.
[21] 谢武仁,杨威,赵杏媛,等. 川中地区须家河组绿泥石对储集层物性的影响[J]. 石油勘探与开发,2010,37(6):674-679.
Research on the Relationship Between Different Types of Reservoirs Physical Properties
1,2,1,1,1
(1. School of Petroleum Engineering, Xi'an Shiyou University, Xi’an Shaanxi 710065, China; 2. Shaanxi Provincial Key Laboratory of Special Production Increasing Technology for Oil and Gas Fields, Xi’an Shaanxi 710065, China)
Based on the experimental data of 179 cores from Daqing oilfield, the permeability of the reservoir was classified, and the relationship between permeability, porosity, median radius, and irreducible water saturation under different classification conditions was discussed,the optimal fitting relationship between permeability and porosity was given, and the correlation between porosity, median radius, irreducible water saturation and permeability was analyzed based on core scanning electron microscope and experimental data.The results showed that the classification based on permeability improved the fitting accuracy of porosity and permeability to a certain extent; for cores with the permeability larger than 100 mD, the correlation with permeability was arranged in descending order: median radius50, irreducible water saturationwi, porosity, among them the median radius was the main controlling factor, and its square value had the best linear correlation with permeability;For cores with the permeability less than 20 mD, the order of correlation with permeability from large to small was as follows: irreducible water saturationwi, porosity, median radius50. When the permeability was small to a certain value, the effect of throat on fluid seepage was weakened, and the influence of pores increased;For cores with the permeability between 20 mD and 100 mD, irrelevant water saturation and median radius had the worst correlation with the permeability. It was recommended to use a power exponential function to fit the porosity-permeability relationship.
Permeability; Porosity; Median radius; Irreducible water saturation; Core experiment; Scanning electron microscope
国家科技重大专项,低渗透致密砂岩气藏压裂裂缝及参数优化(项目编号:2016ZX05050-009);国家自然科学基金青年科学基金项目(项目编号:51704235)。
2021-09-06
刘雄(1988-),男,湖南汨罗人,讲师,博士,从事低渗-致密油气藏提高采收率研究。E-mail:lx06106232@163.com。
严乐(1998-),女,陕西咸阳人,在读硕士研究生。E-mail:2233128087@qq.com。
TE343
A
1004-0935(2021)11-1658-04

