没有“深度”难进“高阶”

劳锡萍

一、把握起始点，铺就思维路线

在教学《三角形的面积》一课前，我们进行了前测。前测中的其中一题如下：

你知道三角形的面积公式吗？

①如果你知道，请你写一写，你是怎么知道的？

②如果你不知道，你认为三角形的面积可能与什么有关系？

我们一共检测了160人，其中知道的占65%，知道的学生中有25%是知道面积公式的由来，有75%说“知道”的学生只是对公式的单纯记忆。不知道的学生占35%，有50%认为面积与底高有关;37.5%认为与长方形、正方形面积有关;还有12.5%说出了把三角形通过割补、拼组转化成长方形或平行四边形。

基于前测的分析，我们考虑在课的伊始，直接引入“三角形的面积”公式。让这些学生暴露已知，满足其展现的心理需求。逆向探究更有利于学生提出问题，触发探究“为什么三角形的面积是这样来求”的问题，从而深度思考如何来验证，解决一系列问题，发展高阶思维。

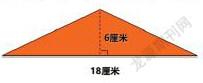
那么，思维的转折点在哪儿？通过面积公式，学生算出了一个等腰三角形的面积。教师引导学生提出问题：这个三角形的面积真的是54平方厘米吗？有没有办法来验证这个答案？这就是这节课的“深度学习点”。

二、把住突破點，寻找思维转折

曾经做过一个小测试：以一张普通的三角形纸片为例题，请学生尝试验证三角形的面积。几乎所有的学生都沿着高剪开，再移至另一边，尝试拼成已经学过的图形。但在反复尝试后，发现无法转化成已经学过的图形。有学生沿着其他的线剪开，依然无法完成转化。

的确，如果让学生突然丢掉这种经验（“割补”），而要求他们寻求另外的方法（“拼组”）来解决问题，这有悖于一般的思维方式。于是，贴着学生的思维，我将普通三角形换成了等腰三角形进行教学。这样顺着学生的思维进行割补转化，而“等腰三角形”的特殊性又为接下去如何验证普通三角形的面积公式铺就了质疑点。

三、把持实践点，给予思维时间

在探究实现等腰三角形的转化过程中，除了用割补沿着高剪开，拼成长方形和平行四边形。通过深度思考、观察操作后，有学生也想到了“拼组”的方法。

【教学片段1】

师：还能转化成什么？

生：可以向同桌借一个三角形，将两个相同的等腰三角形拼成平行四边形。

师：拼出的平行四边形和原来的三角形有什么关系呢？

师：求一个三角形的面积，等于平行四边形的面积除以二。18x6÷2=54（cm2）

在这个过程中，教师给学生提供了充分的思维空间，让学生对“还有别的验证方法吗？”进行主动探寻，学生在动手操作过程中形成的感受成为公式推导的重要感性经验和支撑。从而，实现学生从深度观察到深度思维的深度学习。抓住“转化”的思想，消解学生的思维定势，让学生形成求异、求新的思维。

四、把稳冲突点，寻途思维径向

【教学片段2】

师：刚才我们用特殊的等腰三角形验证了三角形的面积公式。是不是所有的三角形都可以这样来验证呢？请拿出抽屉里的两个普通三角形验证。

（把这些作品贴在黑板上，请学生一起来看。）

师：它们运用了什么方法？

生：割补法、拼组法、两种方法的结合……

师：这幅作品，他错在了哪儿？

教师总结：不管是用割补法还是拼组法都是要将图形转化成已经学过的图形来进行求面积。

“我们用特殊的等腰三角形验证了三角形的面积公式。是不是所有的三角形都可以这样来验证呢？”教师的这一追问，带给学生新的学习任务驱动力。“请拿出抽屉里剩余的两个普通三角形继续验证。”面对新的认知质疑，学生着手完成这具有挑战性的任务。学生运用“割补”和“拼组”进行思维尝试，显露学生思维的过程，让学生的“学”真实发生。

发展学生的高阶思维，需要教师用问题引发学生的深度思考，引发学生的多向交流。教师可以故意设置“障碍”、“漏洞”，激发学生认知冲突，引发学生数学思考。从这个意义上说，发展学生高阶思维的数学深度学习，就是引导学生不断地进行数学探险。

五、把舵创新点，鼓励思维发散

学生在验证普通三角形的面积公式时会出现多种思路。在作品展示环节，有的学生是利用拼组法转化成了平行四边形;有的结合割补法和拼组法转化成了长方形、平行四边形。可见，当学生进行卷入学习时，进行了深度思考、开阔了思维的广度、提升了思维的效度。

学生在激烈的讨论交流中，进行了思维的碰撞，经历了从图形操作到抽象建构的全过程。从而在特定的情境驱动、任务导向下获得了深度体验，不断引导学生超越低阶思维，形成高阶思维能力。

当然，在验证普通三角形面积的环节中，有学生转化成了没有学过的图形。这时候，教师可以为学生提供质疑、辩论的思维平台，让学生通过质疑辩论的方式进入到深度思考活动之中，从而提升学生的思维品质。

综上所述，本文以“三角形面积”的教学为例，阐述了笔者对于“深度学习”理念下，如何培育学生高阶思维发展的看法。我想，“深度学习”的课堂转型，离不开把握认知起点，贴着学情来铺就思维路线;离不开把住突破点，设计合理的学习任务，来驱动思维的发生发展;离不开给予学生充分的思维的时间，来探究认知实践;离不开教师巧妙的追问，来激活认知冲突，提供思维的方向;离不开把舵创新点，鼓励学生自由思考、深度思考。

【参考文献】

[1]王莹.“高阶思维”与学生数学“深度学习”[J].数学教学通讯，2018（19）：13-14.

[2]杨春花.在数学深度学习中发展学生“高阶思维”[J].数学教学通讯，2019（04）：48-49.