基于地面激光点云数据的单木三维重建方法

卢 军,刘宪钊*,孟维亮,李红军

(1. 中国林业科学研究院资源信息研究所,国家林业和草原局森林经营与生长模拟重点实验室,北京 100091；2. 中国科学院自动化研究所,北京 100090；3. 北京林业大学理学院,北京 100083)

地面三维激光扫描(terrestrial laser scanning technology，简称 TLS)用于林业数据测量、森林资源调查与构建树木三维模型已成为近 10 年来的研究热点[1-4]。与传统的测树因子测量相比，具有速度快、精度高、不需要破坏性实验等优点。激光扫描雷达因其发射光源发散性小、探测距离远、精度高等特点，广泛应用于农林作物探测与识别领域[5]。

我国是一个森林资源稀缺型国家，木材安全问题突出，合理利用木材、提高木材利用率是缓解木材安全问题的途径之一。提高树干参数的测量精度，尤其是树干、树枝的测量因子的精度，是林业生产和科研重要的测树因子。从森林经营的角度，现代林业的趋势是集约经营，这就更需要相对精确的生长模型的支持。对单木数据的测量是高精度模型的基础，树木的三维建模为重建树木特征因子提供了可能。基于激光传感器的林木测量技术可得到精度相对较高的林木三维点云数据，并采用合理算法提取基本测树因子数据，是未来精准林业的发展趋势。

TLS 在林业测量上的研究主要包括直径、树高和冠幅的提取，从而获取材积与生物量等[6-7]，以及提取树冠特征结构[8]、提取叶面积指数[9]、构建干曲线方程[10]，在树木三维建模上的研究主要集中在树干骨架提取、枝条模型构建等方面。

树木三维模型的构建是农林业与计算机领域的研究热点[10-11]。使用地面三维激光扫描仪的点云数据对树木重建是一种新的方法，很多研究对树木建模的主要过程及对构建模型的评价方法都有描述[2，12-13]。树木三维模型的构建方法主要分为基于规则的方法、基于图像的方法和基于点云的方法三大类[2]。基于三维激光扫描技术进行树木重建的研究可分为两大类：一类是根据树木点云的空间拓扑关系，用圆柱直接对树木枝干建模；另一类是对树木点云分层，设计相关算法构建出单层点云轮廓线，层与层之间利用三角网格连接，最后构建出整株树木的枝干模型[14-16]。基于规则的三维重建方法是对植物自然生长过程在生态生理方面的动态模拟，通过研究拓扑结构的演变和植物实际生长过程中几何形态的变化，建立其动态结构模型。基于规则的三维重建将动态结构模型分成了字符串重写系统，即L-系统和自动机模型这两种模型[17-18]。

这些方法都有独立的算法，在计算速度和重建结果上各有利弊，而且没有一种方法能整合至工具化，研究者往往都是针对现有数据，经过多步骤的处理，得到重建结果。本研究提出一种基于关键路径探测的新的单木树干、枝条三维结构重建方法，并使用落叶松数据进行实验验证，目的是提高三维重建的效率和质量，通过三维树干、枝条建模，为测树因子提取提供数据基础和技术支持。

1 材料与方法

1.1 数据采集

实验数据来自河北省承德市木兰围场龙头山林场，该地区位于阴山、大兴安岭、燕山余脉的汇接地带，属半干旱向半湿润过渡、寒温带向中温带过渡、大陆性季风型山地气候，以人工林为主，包括落叶松、油松等。本研究的数据来自落叶松样地，面积为25 m×25 m，林分年龄40 a，林分密度600 株/hm2，平均树高21.0 m，平均胸径22.0 cm。为避免细小针叶干扰造成过于密集的点云，不易进行分割，所以数据采集时间为秋天，落叶松已落叶，不存在针叶遮挡的问题。

1.2 点云数据扫描和预处理

使用RIEGL公司的VZ400扫描仪在样地内获取数据，通过5站坐标匹配的方法合成样地的点云数据，使用配准后的点云数据，重建三维树木模型。受粉尘、机身震动等的影响，先对点云数据进行去噪。样地内的灌木和草本对树干下部会产生遮挡，使用交互方式去除灌木和地面。

1.3 构建近邻关系图

离散点和连续点之间如何建立关系，是需要解决的难题。对于离散点集合，本研究通过建立近邻关系图来实现连接。近邻关系图的构建算法主要是把距离较近的点连接起来，其结果与距离阈值δ有关。采用k-d树(k-dimensional tree)来加速近邻查找[19]。

1.4 子图根的求算

先选取比地面高5～10 cm的水平切片作为树的基部，求出基部所有点到平面在Z=Zmin投影点的几何中心Cb,其中Zmin是所求出的最低点的Z坐标值，接着从基部的所有点中选取离Cb最近的点作为这个子图的源点，即全树的根节点。

然后，再确定其余子图的根节点(或称为源点)。这个算法是一个递归的过程：把已经求出源点的所有子图合并在一起构建一棵k-d树T；在所有没有求源点的子图中选择与k-d树T最近的点作为该子图的源点。重复执行这两个步骤，直到所有子图的源点都被找到。

对于每个子图，分别求取子图中各点到根的最短路径。对于每一个子图，用Dijkstra算法求取各个点到源点的最短路径[20]，子图中包含的最短路径数量正好是子图中点的个数。这些路径能够把一些离散的点按照一定顺序连接起来，对于树枝在其直径不是太小的情况下，这些最短路径能描述树枝的连接关系。

1.5 有效路径检测

确定每条路径的末端点和路径中间点，有效路径由非路径中间点定义。上一步得到的最短路径数量太多，有许多点出现在多条最短路径上，因此需要选出这些路径起点，称为有效路径起点，它们仅仅是其中一条路径的起点，但不是其他路径的中间点。有效路径由有效路径起点及其所有后继定义。每一条有效路径的起点都是子图的边界点，而终点都是子图的根节点。在所有路径中筛选出有效路径的算法可以采用一种简单的方法：把通过点vi的最短路径条数称为路过次数,记为N(vi)，初始化所有点的路过次数都为0，N(vi)=0。然后从每条最短路径的起点开始，遍历至根节点，每次遍历过程中经过点的路过次数加1。在O(n)时间复杂度内，所有点的N都能计算出来，这时N值为1的路径起点所确定的最短路径就是有效路径。

1.6 关键路径计算

有效路径都是以子图的根为终点,而起点都是图的边界点，其中那些路径长度较大的能表达这个子图的拓扑结构的有效路径称为关键路径。关键路径的算法采用剔除法，即假设所有的有效路径都是关键路径，再把不合适的剔除即可。先对子图的所有有效路径根据路径长度进行从大到小排序。再从最长的路径开始，从起点遍历至根节点，遍历过程中用半径为r(称为探测半径)的球查找近邻，若近邻中存在有效路径的起点，则标记为剔除。剔除了的有效路径不再进行探测，最后所有没被剔除的有效路径就是关键路径Γ(图1)。查找近邻仍使用k-d树。探测半径r可以是常数，也可以是变量。该算法中采用的是变量r，初始值一般取5 cm，探测过程中，若某次探测的球域内没有有效路径的起点，则半径r适当增加[21]。

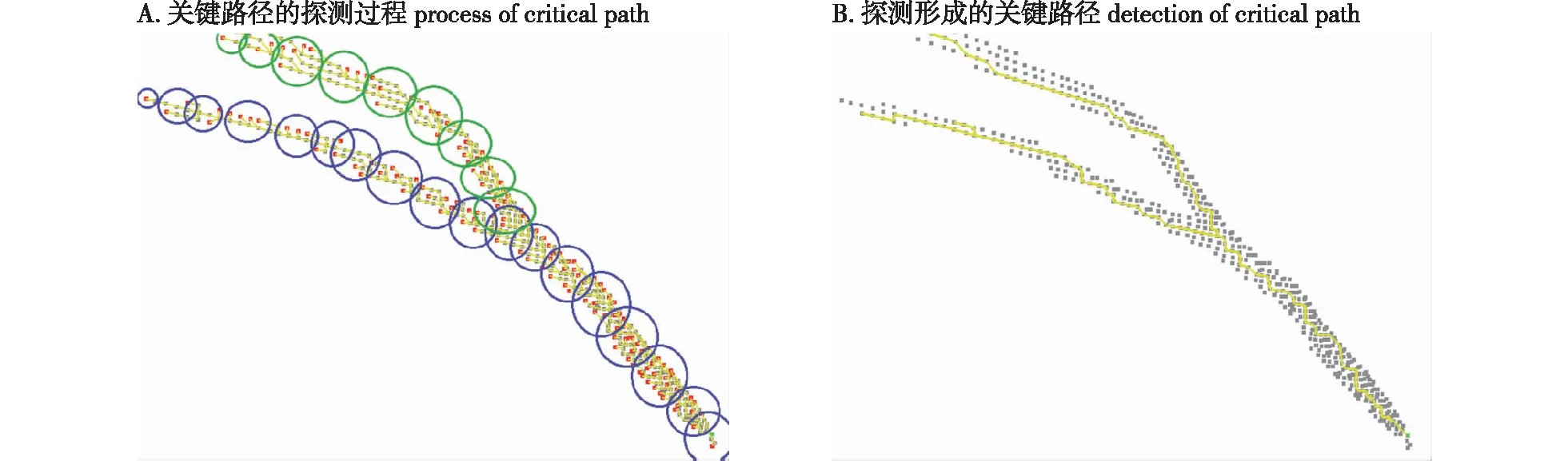
图1 关键路径的计算Fig.1 Calculation of critical path

图1A中的灰色的点为扫描点，红色的点为有效路径的起点，黄色的为有效路径，起初的探测为蓝色圆所示意，探测的方向为从末端(左上方)到子图的根节点(右下的绿色点)，探测过程中，探测半径逐渐变大，其原因是树枝的半径逐渐变大。绿色圆圈为另一条路径的探测过程，在分叉处遇到已经求取的关键路径后，它不再继续探测，因而也确定了一个分枝点。图1B为求出的两条关键路径，其余的有效路径都已被剔除，因此这实际上已经初步得到了树枝骨架的雏形。

1.7 树枝骨架计算

从关键路径中选出树枝的骨架，并计算每一个骨架的初始半径。首先，从关键路径的起点到根节点，依次计算每个节点的半径。计算的方法采用圆柱拟合，或者投影的圆拟合，或者投影包围盒换算。这里考虑了几种可能遇到的情形：①进行圆柱拟合，求取对应点p的半径；②若拟合检验不能通过，则把所有近邻点投影至过点p的拟合平面π上，再进行圆的拟合；③若拟合不足(比如只有2个近邻点或者多个近邻点共线等异常情况)，则直接计算投影点在这个平面上的矩形包围盒，设这个包围盒的两邻边长为a、b(a≥b),则点p的半径Rp估计值为：

(1)

半径估计过程中，若某个关键路径Γ的起点属于另一个关键路径中某个骨架点半径范围之内，则把Γ从关键路径中剔除，最终的关键路径构成这棵树的初始骨架。

1.8 半径平滑

自然生长的树木每个枝干表面基本上是光滑连续的，这意味着树枝骨架节点的半径也基本符合植物学经验公式，相邻骨架点的半径基本上是平滑过渡的。由于过拟合、拟合不足或者噪声干扰等各种原因，初始骨架的半径有可能不平滑，需要对半径作一次平滑处理。对于枝的末端半径，对枝末梢的n个骨架点的半径进行统计分析：

首先，计算半径区间[Rmin,Rmax]；然后，把区间分成k等分,得到k个分割区间[Rmin+idr,Rmin+(i+1)dr],其中i=0,…,(k-1)，Rmax=k·dr，dr=(Rmax-Rmin)/k；对这n个骨架点的半径在各个分割区间进行统计计数，计数结果记为ni,i=0,…,(k-1)。

去掉首尾两个区间的频数之和记为n*=n1+…+nk-2,则第n/2个骨架点半径的估计值为：

(2)

式中：c为用户指定的树枝末端最小半径,γ为末端半径平滑衰减系数，实验中一般对同一棵树取为定值(c=0.01 cm，γ=0.998)。

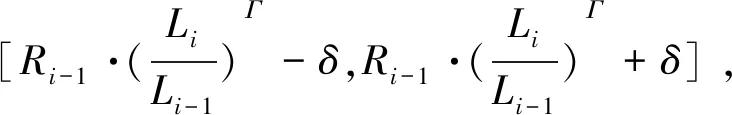
(3)

式中：R为第i节点的半径，Li为第i节点之后的树枝长度，根据前人的研究结果，参数Γ一般取值为2/3[13,22]，本研究经过实验令Γ=1/2。事实上，这反映树枝半径的衰减信息，与树种有关。

1.9 骨架平滑、连接与网格模型构建

把原有骨架点作为控制点，利用Bezier曲线进行平滑。从包含整个树的树根开始，根据距离最近原则逐步把其他树枝连接到这个子图中，使整棵树的骨架连接在一起。

构建树枝表面网格模型，配置树叶及其纹理，重建树木三维结构。获得每个节点的半径后，就可以骨架点为中心，相邻骨架点连线为轴，构建圆台侧面，同一个树枝的所有圆台侧面连接成整体，形成树枝的表面网格模型，再配上树皮纹理信息，绘制树枝模型。

所构建的模型与过去的算法相比，不仅树木主枝构建准确，细枝的连接关系也比较可靠。

2 单木三维模型重建结果

2.1 点云预处理

使用样地内的3棵落叶松来展示模型重建的中间结果(图2)。

图2 落叶松a、b、c点云数据原始数据的预处理Fig.2 Preprocessing of initial cloud point data for three larch trees

落叶松a原扫描点云数据共128 237个点云，处理后75 214个；落叶松b扫描点云共97 822个点云，处理后59 143个；落叶松c扫描点云共104 369个，处理后88 103个。预处理不能影响重建的效果。

2.2 近邻关系构建

对3株落叶松的近邻关系进行构建，并计算每个子图的根(图3)。其中，落叶松a计算用时0.429 4 s，共有113个子图；落叶松b计算用时0.577 1 s，共有134个子图；落叶松c计算用时0.731 6 s，共有189个子图。

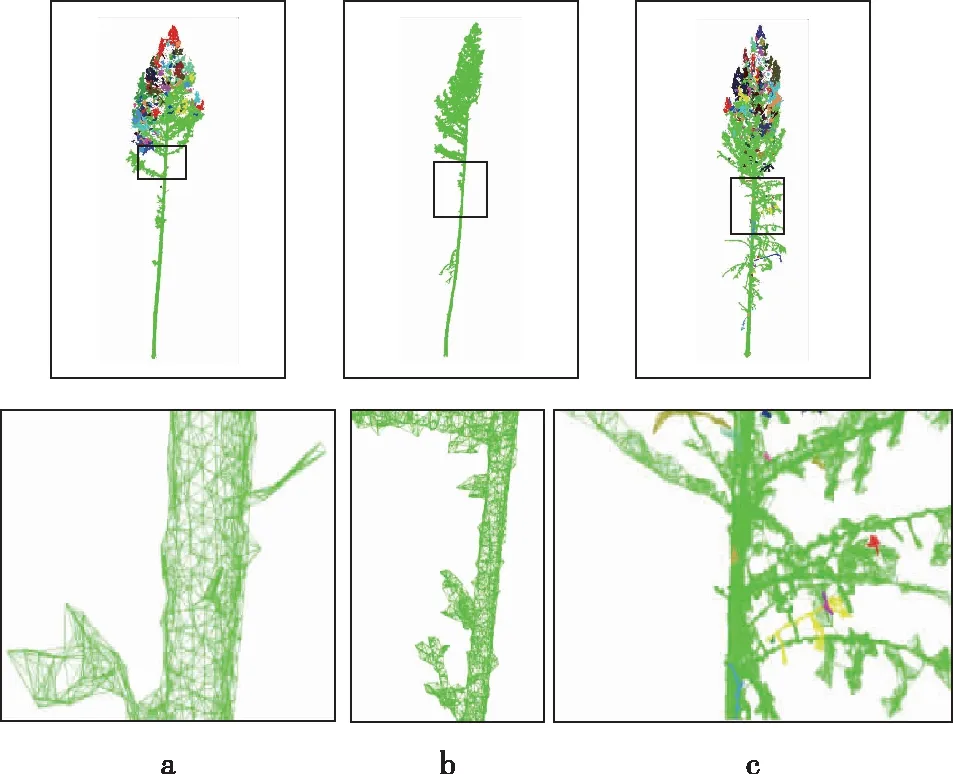
图3 3株落叶松的近邻关系求算Fig.3 The adjacent relationship among point cloud for three larch trees

2.3 最短路径、有效路径及关键路径计算结果

3株落叶松最短路径计算结果见图4，计算结果表明，a、b、c 3株落叶松最短路径计算时间分别是6.157 8、0.101 3和17.327 5 s，落叶松c计算时间最长，这和树枝的复杂程度密切相关。

图4 3株落叶松最短路径计算结果Fig.4 Shortest path calculation for three larch trees

有效路径检测结果见图5，落叶松a、b、c的有效路径检测时间分别是1.309 4、2.128 4和2.137 8 s。

图5 3株落叶松有效路径检测Fig.5 Testing of effective paths for three larch trees

3株落叶松关键路径计算结果见图6，落叶松a、b、c的关键路径计算所需时间分别是1.962 3、3.278 3和4.693 4 s。通过这个步骤，枝条的细节已经能展示出来，尤其是一级枝清晰可见。

图6 关键路径计算结果Fig.6 Calculation of critical paths for three larch trees

2.4 树枝骨架计算、三维骨架平滑及骨架连接

3株落叶松树枝骨架计算结果见图7，落叶松a、b、c计算分别耗时0.291 7、0.090 3和0.723 9 s。

图7 树枝骨架计算结果Fig.7 Skeletons of branches calculation for three larch trees

三维骨架平滑结果见图8，经过半径平滑和骨架平滑后，得到树干、树枝的骨架模型，分别耗时0.194 0、0.018 4和0.268 1 s。

图8 骨架平滑结果Fig.8 Smooth of skeletons for three larch trees

把所有的骨架连接起来，就得到整株树木的骨架结构。落叶松a树冠内部存在遮挡，耗时39.163 8 s计算得出；落叶松b耗时0.920 9 s；落叶松c的节间数较多，连接过程复杂，共耗时67.552 7 s。

对比另外一种基于Dijkstra距离分段的骨架构建方法[23]，所使用的深山含笑(Micheliamaudiae)6 885个点，樱花(Sakurasp.)36 996个点，计算时间分别是54 s和309 s，本研究对3株落叶松的计算时间分别约为39、0.9和67 s，计算速度有很大的提高。

2.5 树木网格模型建立结果

得到的网格模型，需要与预处理后的点云数据进行匹配，匹配的图像见图9。

图9 网格模型与点云数据的匹配Fig.9 Matching of surface model and point cloud for three larch trees

红色的离散点能够附着在网格模型上，匹配率分别为95.5%、97.6%和95.3%，均超过了95%，效果较好。

落叶松a骨架数516个，节间数7 845个；落叶松b骨架数118个，节间数4 298个；落叶松c骨架数448个，节间数12 631。通过这种基于关键路径探测的重建方法，可以得到精度较高的树干、树枝三维模型。

3 讨 论

树木具有复杂的结构，尤其是树冠部分，细小的三级枝甚至四级枝交错在一起，给三维重建带来了巨大的挑战。本研究是一种方向优化策略的单株木重建，从有效路径中探测、提取关键路径，形成具有分枝层次结构的树枝骨架，最后通过平滑处理建立单木的三维树干树枝的表面网格模型。该方法能够对落叶松的细小枝条进行重建，通过观察重建结果，一级枝的重建效果非常好，大的二级枝也能得到很好的展示，但是三级枝往往很破碎，效果一般，这是重建工作的共同难题。另外这个方法能充分使用扫描数据来更精确地构建树木的拓扑结构。

以往的树木三维重建研究是通过圆柱拟合技术进行树木重建[24]，对大的树枝重建结果较好，但对细枝尤其是二级枝、三级枝或者点云稀疏的情况，会出现拟合不足。通过最小树(minimum spanning tree)方法进行树木重建可以得到细枝，但树枝分枝时的参数难以确定，以至放弃细枝的重建而采用L 系统进行模拟[25]。以往的研究未能解决细枝重建问题，本研究中的关键路径检测和骨架连接等技术提出了一种重建细枝的方法。

树的结构比一般的点云模型复杂许多，树干、树枝和树叶之间的遮挡很普遍，点云分布不均匀，团状、线状和簇状的点云给重建带来了极大难度，同时树皮的开裂和脱落方式不同，树干的粗细变化很大，枝的分枝结构繁杂，这使得重建结果的连接存在错误。由于离散点很多，也有点云密度不足的情况，树枝尤其是细枝的重建结果至关重要。本研究的这种方法匹配率较高，可以应用于林业单株木测树因子的获取。

4 结 论

1)通过近邻关系可建立点云的有效路径，探测树干和枝条的关键路径，计算得出骨架模型，使用现有的点云数据可构建树木的拓扑结构。

2)使用k-d树和Dijkstra算法计算得出树干和枝条的骨架，再进行平滑计算，使得骨架模型更贴合点云。

3)使用半径平滑和圆柱拟合减少点云密度小造成的拟合不足的情况，能够最大限度保留树枝的细节。进行骨架连接后得到树干树枝的三维网格模型，与点云匹配后，效果较好。

4)整套算法计算时间快速，计算时间与枝条的复杂程度、连接关系有关。下一步的工作是在重建的三维模型的基础上自动和半自动地提取高精度测树因子，如任意位置处的直径、枝条信息等，很大程度地解决现有的测树数据获取难度大、破坏性提取的问题。