基于神经网络的声场景数据声谱图提取方法
韦 娟, 丁智恺, 宁方立
(1. 西安电子科技大学通信工程学院, 陕西 西安 710071; 2. 西北工业大学机电学院, 陕西 西安 710072)
0 引 言
声音场景分类是计算机听觉(computer audition,CA)领域的重要研究方向,声音场景识别可以作为声音事件的辅助手段[1],并且音频特征可以与视频特征结合共同完成分类任务[2],对于实际应用具有重要意义。对于不同的音频分类任务,CA领域逐渐形成了一套通用技术流程[3]:首先采用麦克风等声音传感设备采集音频信号,并使用重采样、解压缩等方式进行预处理;通过音频事件检测或端点检测将有用的音频信号分割出来;然后通过消噪等方式加强音频信号;最后提取音频特征或者直接采用音频波形作为输入,使用深度学习(deep learning,DL)模型或其他统计分类器识别。
在以往的研究中,先对原始音频进行特征提取,再使用卷积神经网络(convolution neural network, CNN)类网络进行识别,并取得了不错的成效。Mesaros等[4]对DCASE2017比赛的成果做出总结,表明目前声音场景分类最常用的特征是短时傅里叶变换(short time Fourier transform,STFT)、对数梅尔频谱系数(log Mel-frequency spectral coefficients, MFSC)、梅尔频率倒谱系数(Mel-frequency cepstral coefficient,MFCC)等二维谱图,其优点在于将原始信号转变为紧凑的时频表示,并且能够使用CNN类网络进行分类[5-9]。
虽然二维声谱图在音频识别任务中取得了高识别率,但是以原始声音波形作为模型的输入仍是研究的热点,因为无法保证依据人类听觉生理特点设计的梅尔滤波器组是最佳滤波器组[10],并且图像输入容易被干扰使得CNN类模型不能正确识别[11]。Jongpil等[12]类比牛津大学科学工程系视觉几何团队的神经网络架构(neural network designed by visual geometry group, VGG)网络架构,使用一维卷积网络处理原始波形用于音乐分类,类似的模型[13-16]在语音检测、语音情感识别等诸多领域有着广泛使用。卷积长短期记忆深度神经网络(convolutional long short-term memory, deep neural networks, CLDNN)以及衍生架构[17-20]常用于识别语音等音频的声谱图,Zazo等[21]用一维CNN取代STFT的提取过程使得CLDNN能以原始波形作为输入,在语音识别任务中取得了较高的识别率,类似的网络结构[22]也被用于语音情感识别。Tokozume等[23]提出用于环境声分类的端到端卷积神经网络(end-to-end convolutional neural network for environmental sound classification, EnvNet)网络,在输入部分用一维卷积,再将一维卷积的结果输入二维卷积网络用于识别环境声,类似的架构[24]也被用于声音事件检测。
通过在DCASE2019声场景数据集上训练并测试了大量现有架构,得到了以原始波形作为输入的架构识别率不如以声谱图作为输入的CNN类网络的结论。以原始音频波形作为输入的架构优点在于从原始波形提取特征的过程可以被训练,以声谱图作为输入的架构优点在于声谱图物理意义明确且适合使用CNN识别。结合这两类架构的优点提出声谱图提取神经网络(spectrogram extraction neural network,SENN),使用神经网络提取MFSC,然后连接50层的残差神经网络(50-layer residual neural network, ResNet50)组成整个模型,通过训练SENN优化声谱图。
1 SENN
1.1 MFSC提取网络
目前以原始波形作为输入的架构在神经网络浅的层多采用一维卷积层模拟声谱图提取的过程[12,21,23],基于此推导了MFSC提取和神经网络卷积运算的关系,从而构建以卷积层为核心的SENN。
MFSC提取流程是:首先对音频信号分帧、加窗,接着对每帧信号进行离散傅里叶变换(discrete Fourier transformation,DFT)并拼接成二维张量,然后取模值得到STFT谱图,最后通过梅尔滤波器组取对数得到MFSC谱图[25]。
1.1.1 DFT与一维卷积层
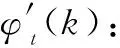
(1)
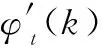
(2)
式中:i=0,1,…,N-1。将实部记为Ct(i),虚部记为St(i)。现讨论Ct(i)与一维卷积的关系,由式(1)与式(2)可得
(3)
卷积运算的原理[26]:输入张量A的第m个通道的第n个元素记为An,m,卷积核W的第i个子卷积核的第m个通道的第个k元素记为Wk,m,i,A与W进行步幅为s的卷积运算得到输出张量B,B的第i个通道的第t个元素记为Bt,i,满足关系:
(4)
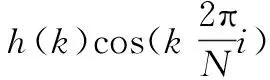
(5)
同理可得St(i)与一维卷积的关系:
(6)
1.1.2 梅尔滤波器组与二维卷积层
MFSC谱图的提取由DFT矩阵与梅尔滤波器组运算得到,这一部分可以由二维卷积运算实现。二维卷积运算的原理为:输入张量D的第m个通道的第n行p列元素记为Dn,p,m,卷积核W的第i个子卷积核的第m个通道的第x′行y′列元素表示为Wx′,y′,m,i,D与W进行高度步幅为sx宽度步幅为sy的卷积运算得到输出张量E,E的第i个通道的第x行y列元素记为Ex,y,i,满足关系:
convx,y,i(D,W)
(7)

(8)

取对数得到对数MFSC矩阵,记为MFSCdB:
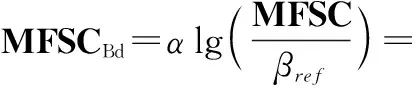
(9)
式中:βref是MFSC的参考值;α是缩放系数。整理后得到由缩放系数k和偏置b决定的MFSCBd,参数k与b可训练,实验过程中k初始化为20,b初始化为100。接着给MFSCBd添加通道维度作为CNN类识别架构的输入。根据MFSC提取过程与卷积层的关系设计SENN得到MFSC提取神经网络(MFSC extraction neural network, MFSCNN)。
1.1.3 MFSCNN结构
MFSCNN结构如图1所示。R和I的通道数为1、卷积核长度等于帧长N、子卷积核个数为N/2+1,卷积步幅等于帧移s;FB的长度为1、通道数为N/2+1、子卷积核个数为M,卷积步幅为1。在处理DCASE2019的数据时,N=2 048,s=1 024,M=128,得到469帧,128阶的MFSC谱图。传统MFSC提取方法和经过初始化的MFSCNN处理DCASE2019声场景数据集中的“airport-barcelona-0-0-a.wav”,得到了相同的结果如图2所示。这说明通过R和I对MFSCNN进行初始化,能够在未经训练的情况下从原始音频中提取MFSC谱图,MFSC的提取过程将通过训练MFSCNN得到优化。

图1 MFSCNNFig.1 MFSCNN
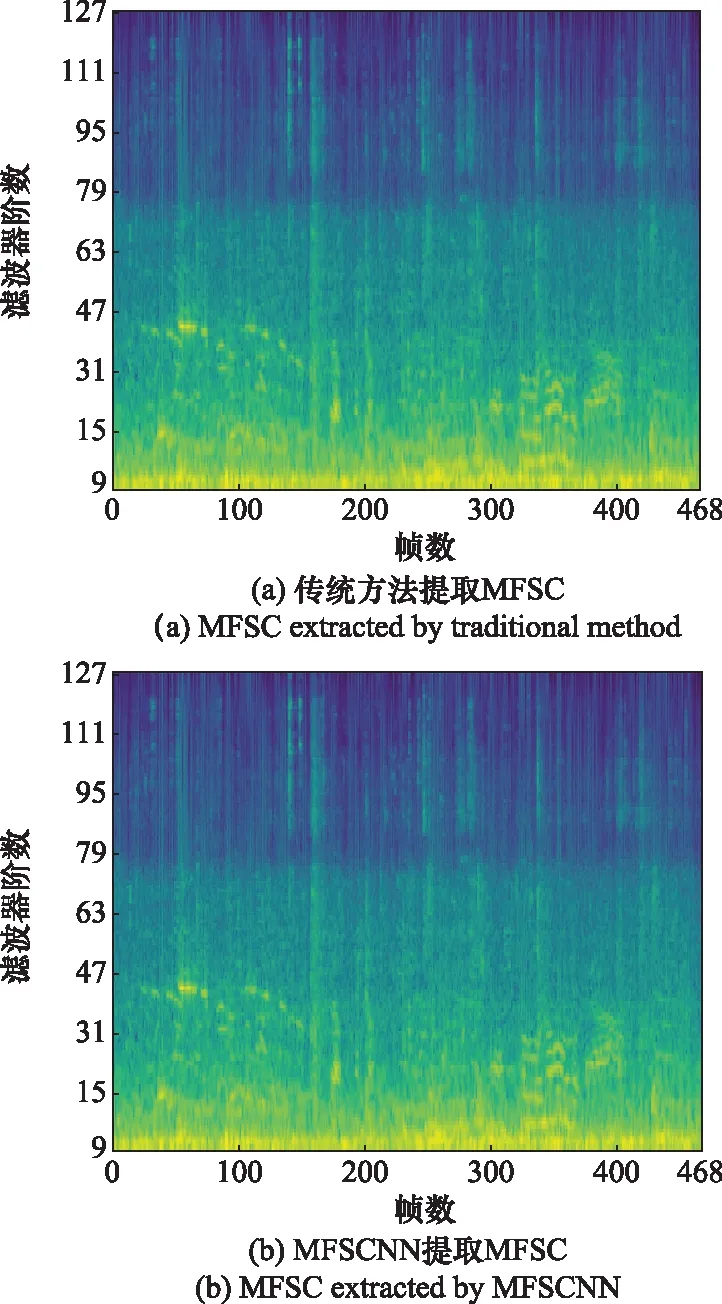
图2 传统方法与MFSCNN提取MFSC对比Fig.2 Comparison of traditional method and MFSCNN to extract MFSC
虽然MFSCNN在结果上复现了MFSC谱图,在结构上使得特征提取过程可以被训练,但是训练结果(详见实验结果与分析)表明该架构对识别率的提升有限。因此,本文改进MFSC的提取过程得到对数梅尔频率傅里叶变换谱系数(log Mel-frequency Fourier transform spectral coefficients,MFFTSC),并设计相应的神经网络结构解决MFSCNN难以训练的缺点。
1.2 MFFTSC提取网络
1.2.1 MFSCNN的缺陷与改进
网络参数中滤波器组幅值系数H训练效果明显,但R、I和FB′没有得到有效训练,这是由于这3个卷积核参数量过多造成的。在实际训练过程中,R和I的参数量均为2 048×1×1 025,FB′参数量为1×1 025×1×128,对于R和I既不能保证训练后每个子卷积核只包含单一频率又不能保证子卷积核按频率顺序排列,对于FB′则不能保证每个滤波器只关注某个连续的频段。因此,对MFSC提取过程和MFSCNN做如下改进。

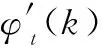

采样率为fs时,根据数字角频率θ和实际频率freal的关系θ=2πfreal/fs,以及梅尔频率fmel与freak的关系fmel=Mel(freal),推导梅尔离散时间傅里叶变换(Mel discrete time Fourier transform,Mel-DTFT),结果记为φt(fmel),满足:

(10)
对Mel-DTFT在频域上离散化得到Mel-DFT:
MelDFTt(i)=
i=0,1,…,L
柿叶很少发病,但病菌却是通过叶片传播的,因为阴雨或高温天气产生的病菌附着到叶面上,叶片发病脱落时营养回流,病菌由芽眼进入主干,在芽下方形成三角形病斑,病菌主要以菌丝体在枝梢病斑中越冬,也可以分生孢子在病干果、叶痕和冬芽等处越冬。来年随萌芽展叶和树体生长,病菌向上移动,在芽周围形成菱形病斑,造成芽部塌陷,影响到树体生长。一般年份,枝梢6月上旬开始发病,雨季为发病盛期,秋梢可继续受害;果实发病时期一般始于6月下旬至7月上旬,直至采收期,发病重时7月下旬果实即开始脱落。
(11)
式中:fl是被研究频段的最低频率;fh是被研究频段的最高频率;L越大Mel-DFT频域分辨率越高。式(10)和式(11)不仅适用于梅尔频率标度,其中Mel(·)可以替换成任何频率曲线关系式,进而完成相应频率标度的DTFT与DFT。
接着使用一维卷积实现Mel-DFT的实部和虚部。具体地,式(5)和式(6)中I和R满足新的表达式:
(12)
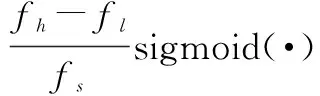
(13)
实验过程中fl=0,fh=fs/2,L=1 025。根据MFFTSC提取过程设计第二种SENN得到MFFTSC提取神经网络(log Mel-frequency Fourier transform spectral coefficients extraction neural network,MFFTNN)。
1.2.2 MFFTNN网络结构
MFSCNN改进后得到第二种SENN,即MFFTSC提取网络,记为MFFTNN。为了保证频率曲线更快地收敛,使用两层全连接层对ω进行辅助训练,然后连接ResNet50进行整体训练,架构整体称为声谱图提取识别模型如图3所示。辅助训练网络以及识别网络中的全连接网络(fully connected neural network, FC-Net)均采用隐藏层512个神经元(激活函数为sigmoid),输出层10个神经元(激活函数为softmax)的结构。特别地,辅助训练网络先对Mel-DFT的模值矩阵沿着帧数轴进行平均池化将469帧1 025个频点的Mel-DFT模值矩阵池化成长度为1 025的特征向量,对应整个音频的频域,然后通过全连接网络进行识别。辅助训练网络的主要作用是对决定频率曲线的参数ω进行预训练。

图3 声谱图提取识别模型Fig.3 Spectrogram extraction and recognition model
将图2所用音频作为MFFTNN的输入,对比MFFTNN与MFSCNN的可视化输出如图4(该图截取了两个声谱图“声纹”明显的部分:横轴280~420帧,纵轴0~40阶)所示。
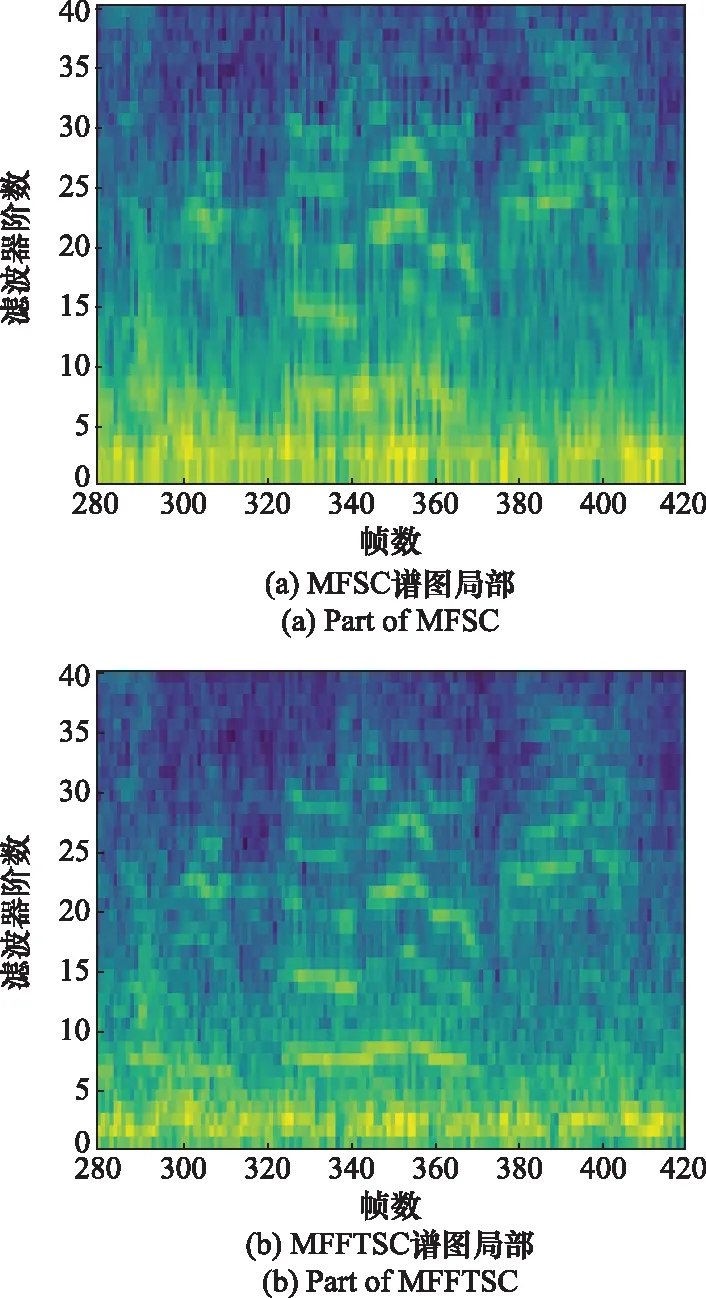
图4 MFSC与MFFTSC局部对比Fig.4 Partial comparison between MFSC and MFFTSC
2 实验结果与分析
实验数据选用DCASE2019年比赛中“Task 1. Acoustic Scene Classification”的公开数据集。该数据集包含10类城市声音场景,分别是机场、公交、地铁、地铁站、公园、广场、商场、人行道、公路、有轨电车。每类音频包含1 440个数据,整个数据集合计14 400个数据。每个音频采样率为48 kHz,时长为10 s,双声道,精度为24位。采用五折交叉验证对数据集进行划分,损失函数选择交叉熵损失函数,训练器选择随机梯度下降优化算法,批量大小设置为32。表1给出了传统识别模型以及本文提出的识别模型的识别率对比。具体结构为:一维卷积层(one-dimensional convolutional layer,conv1d),二维卷积层(two-dimensional convolutional layer,conv2d),全连接层(fully connected layer,fc),长短期记忆层(long and short-term memory,lstm)。在这些结构前用整数表示堆叠层数(无整数时表示单层结构),“resnet50”表示ResNet50的CNN部分,“vgg19”表示包含19层神经网络层的VGG的CNN部分。各种架构的具体训练过程如下:传统识别模型包括以原始波形作为输入的传统架构(表1中实验1~实验3)和以二维张量作为输入的传统架构(表1中实验4~实验7),这些模型的初始学习率设置为0.01,每隔10轮训练将学习率减小为之前的1/10,直至损失值收敛且学习率稳定。
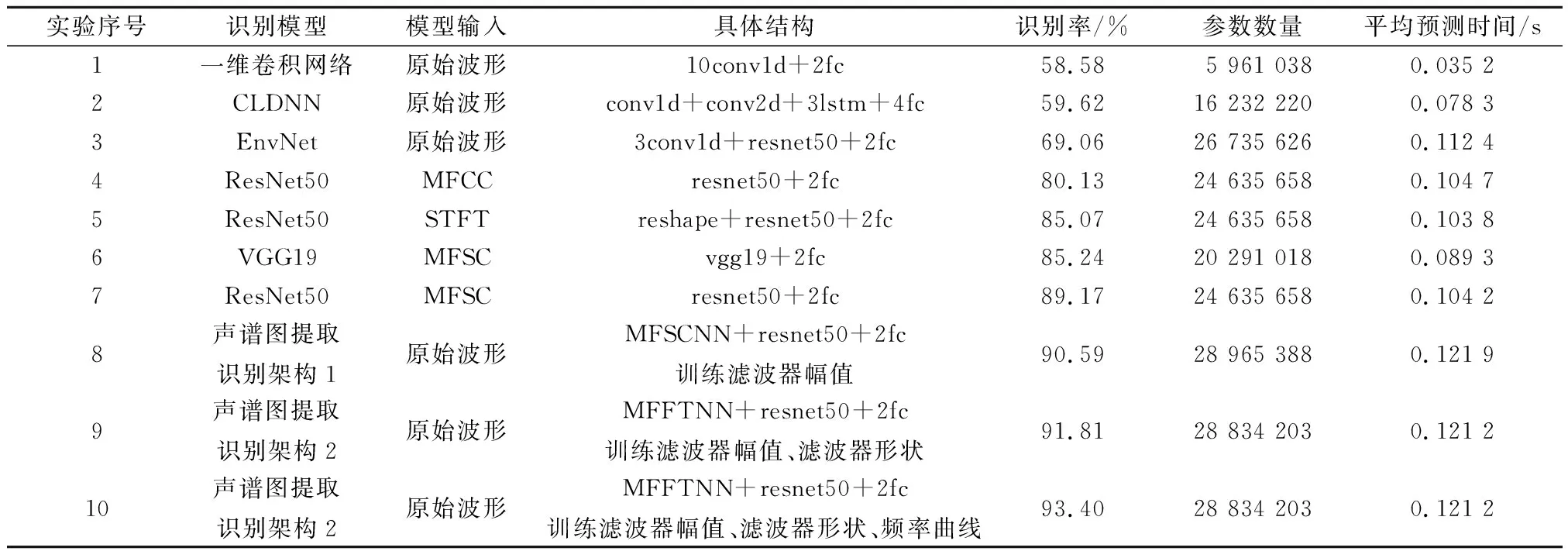
表1 模型性能对比
针对第一种架构“MFSCNN+ResNet50”,若采用与传统方法相同的训练过程,识别结果与EnvNet类似。本文采取的训练方式是前10轮将MFSCNN的参数设置为不可训练,仅训练ResNet50。再训练模型整体,此方法可以有效提高识别性能。MFSCNN的参数包括与STFT对应的卷积核、与梅尔滤波器组对应的卷积核、滤波器幅值系数以及分贝层参数。在DCASE2019声场景数据集上同时训练4种参数与仅训练滤波器幅值系数的识别率并无明显差别,表1给出仅训练滤波器幅值系数时的实验结果(实验8)。
第二种架构“MFFTNN+ResNet50”研究滤波器幅值系数、滤波器形状以及频率曲线对识别性能的影响:① 忽略辅助训练结构且训练过程与第一种架构一致,仅训练滤波器组幅值系数识别性能与第一种架构相差无几;② 忽略辅助训练结构且训练过程与第一种架构保持一致,训练滤波器组幅值系数以及滤波器形状得到的实验结果如表1中实验9所示;③ 通过辅助训练结构对频率曲线进行预训练(预训练过程为:初始学习率设置为0.01并将MFFTNN的参数设置为不可训练,训练辅助结构的两层全连接网络共训练10轮;接着将学习率减小至0.001,训练两层全连接网络和MFFTNN中决定频率曲线的参数ω,共训练10轮),然后训练过程与第一种架构一致,训练滤波器组幅值系数、滤波器形状以及频率曲线得到的实验结果如表1中实验10所示。
传统模型的识别性能:对比实验1~实验3与实验4~实验7得出结论:在DCASE2019声音场景数据集上,以原始波形作为输入的架构识别率不如以声谱图作为输入的架构。由实验6和实验7得出结论:在本数据集上ResNet50比VGG19具有更高的分类性能。由实验4、实验5和实验7得出结论:采用ResNet50识别MFSC、MFCC、STFT这3个声谱图,具有最高识别率的是MFSC。
声谱图提取识别模型的分类性能:由实验7~实验10得出结论:声谱图提取识别模型采用SENN替代传统声谱图提取过程使得滤波器幅值、滤波器形状、频率曲线被有效训练,这3组参数对识别率都有积极的影响,最终识别率比传统架构提高4%。对比实验3与实验8~实验10得出结论:虽然声谱图提取识别模型与EnvNet有相似之处,但声谱图提取识别模型识别率比EnvNet高很多,原因是本文的架构在声谱图提取部分采用了两路并行卷积实现Mel-DFT的实部与虚部,并通过平方层、滤波器组层、分贝层复现声谱图提取的过程,每一部分都有明确的初始权重,能够在未经训练的情况下直接得到类似于MFSC的谱图,而EnvNet只是简单地串行连接卷积层,很难通过初始化得到类似于MFSC的谱图,在该数据集上未经初始化的一维卷积层难以被有效训练,因此本文的架构识别率远超EnvNet。
声谱图提取识别模型的参数量:SENN参数约占总体模型的15%,ResNet50约占85%,SENN是一个轻量级的网络,与现有的DCNN类模型相结合不会使参数量大幅增加。
声谱图提取识别模型的运行时间:“SENN+ResNet50”比“ResNet50识别MFSC”的运行时间多16%,对每个音频的平均预测时间为0.121 2 s,对于一般的应用场景,能满足实时性要求。滤波器形状训练结果如图5所示。滤波器初始化为三角滤波器,如图5(a)所示;经过训练滤波器形状发生改变,如图5(b)所示,训练MFFTNN能够对滤波器的形状做出调整进而提高识别率。频率曲线训练结果如图6所示。频率曲线初始化为梅尔频率曲线,曲线斜率越大频率信息被保留的越多。梅尔频率曲线训练后如图6红色曲线所示。MFFTNN在梅尔频率曲线的基础上对不同频点的斜率进行调整以适应数据集,进而提升识别率。滤波器组幅值系数训练结果如图7所示,每个滤波器幅值各不相同,均在1.0上下浮动,说明通过训练MFFTNN可以调整声谱图不同频率成分的强度。
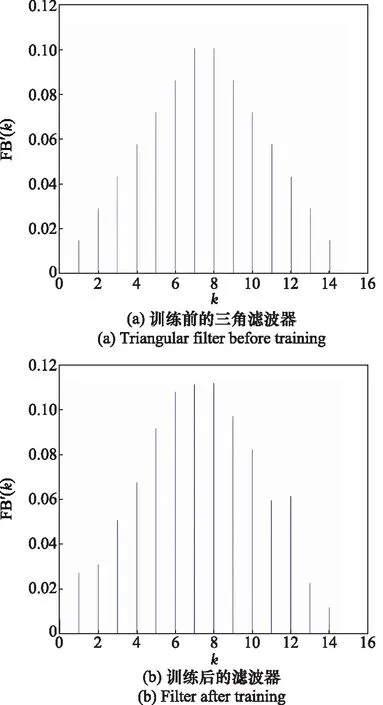
图5 滤波器形状训练结果Fig.5 Filter shape training results
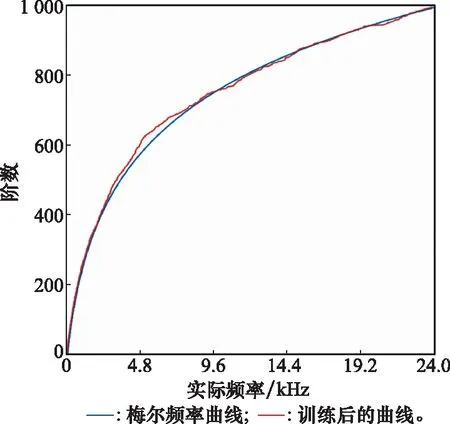
图6 频率曲线训练结果Fig.6 Training results of frequency curve

图7 滤波器幅值系数训练结果Fig.7 Training results of filter amplitude coefficient
3 结 论
为了使得声谱图能够根据当前数据集自动调整,设计了第一种SENN即MFSCNN用于取代传统梅尔频谱提取过程,实验结果表明滤波器幅值系数得到有效训练但是梅尔滤波器组并没有得到有效训练,因此改进MFSCNN得到第二种SENN即MFFTNN,使得梅尔频率曲线和滤波器形状也得到训练。实验结果表明,MFFTNN的识别率明显优于传统架构,具体如下:① MFFTNN除了易于训练之外,其输出的声谱图还具有在低频部分的分辨率高的特点;② 训练MFFTNN能够调整声谱图的频率曲线、滤波器形状、滤波器幅值系数,这3组参数对识别率均有积极影响,最终识别率比传统架构提高了4%;③ MFFTNN是轻量级的网络,与深度卷积神经网络相结合不会大幅增加模型大小和预测时间,对每个音频的平均预测时间为0.121 2 s,满足一般应用场景的实时性要求。

