太阳能光伏发电项目风险评价

靳波

摘  要：针对太阳能光伏发电项目建设风险评估的需要，根据太阳能光伏发电项目的特征，构建项目风险评价指标体系，然后应用粗糙集理论和模糊层次分析法对某太阳能光伏发电项目进行实证评价。结果表明：该项目的总得分为81.08，风险属于良好等级。而通过研究看出，模糊综合评价在应用的过程中，关键是要计算权重，然后再构建评价集，进而求得评价结果。

关键词：太阳能   风险评价   粗糙集   模糊层次分析法

中图分类号：TM62                          文献标识码：A文章编号：1672-3791（2021）07（c）-0026-03

Abstract： According to the needs of construction risk assessment of solar photovoltaic power generation project， according to the characteristics of solar photovoltaic power generation project， this paper constructs the project risk evaluation index system， and then makes an empirical evaluation of a solar photovoltaic power generation project by using rough set theory and fuzzy analytic hierarchy process. The results show that the total score of the project is 81.08， and the risk belongs to good level. The research shows that in the application process of fuzzy comprehensive evaluation， the key is to calculate the weight， and then construct the evaluation set to obtain the evaluation results.

Key Words： Solar energy; Risk assessment; Rough set; Fuzzy analytical hierarchy process

隨着经济的发展，我国对能源的需求越来越大。光伏能源作为一种新型的能源，正在成为我国能源产品的一个补充，并成为一个新兴的产业。光伏能源拥有可再生、无污染、减排和节能的优点，具有很大的开发潜力，受到许多企业的青睐。因此，加强对光伏项目的建设，成为当前光伏投资建设的重点。但光伏项目的建设周期长、投资大，从而使得项目建设存在很大的不确定和风险[1-2]。因此，加强对光伏项目的风险评估，对减少项目建设的风险很有必要。该文则根据项目特点，提出一种定量的风险评估方法。

1  方法原理

1.1 粗糙集理论

粗糙集理论是一种用于处理不确定性的数学方法，其核心内容是知识约简，即在保持信息系统分类能力不变的条件下，去掉多余的属性，从而获得最佳属性，实现信息系统的优化。假设一个决策系统S=（U，A，V，F）表示，其中U为论域，是一个非空有限集合;A=C∪D，为属性集合，其中C表示条件属性，D表示决策属性;V为属性值域;f：U×A→V为信息函数[3]。

二维决策表表示一个决策系统，其中的列表示属性，行表示对象。如果属性集合BA，且存在[4]：

则R（B）为不可分辨关系，即B中的任意两个对象x，y对于B都为不可分辨的。若a∈B，则：

另外，在粗糙集理论中包括正区域、负区域和边界区域。如果有限集合XU，则X的B下近似B-（X）和上近似B-（X）为：

式中，3个不相交的区域U为正区域、负区域和边界区域，分别为：

U的划分是粗糙的，所以用αB（X）近似精确度来表征这种粗糙度。

如αB（X）=1，表示B可以完全分辨;如果αB（X）=0，则B不可完全分辨。

上述中的决策属性D对条件属性C有一定的依赖程度，具体依赖计算公式为：

其中|POSC（D）|为，|U|为U的势。条件属性子集ciC对D的重要度为：

1.2 模糊层次分析法

模糊层次分析法是常用的定量分析方法，其主要原理是利用最大隶属度原则，根据属性分类，用模糊综合评判每一类中的各个因素，再用评判结果对各类指标进行更高层次综合评判，最后得到评价结果。具体可分为以下几个步骤[5-6]。

一是建立评判因素集u（评语集）和v（评价指标集），v=（v1，v2，...，vm），u=（u1，u2，...，un）。其中n表示指标个数，m表示不同的评价结果。

二是确定评价指标的权重W。通常指标权重的确定采用层次分析法中的最大特征值λmax进行计算。

最大特征根中，P为判断矩阵。

三是建立单因素评判。对各个指标进行评价，从而确定评价矩阵。通常邀请N名专家对各个指标进行打分，从而得到R，然后得到评价矩阵为R=[r1，r2，...，rn]T。指标的综合评价计算为：

四是模糊综合评价。根据上述计算得到的R=（K1，K2，…，Ki）T，然后根据下式计算：

S=W×R

最后综合评价值用P=S×V T计算。

2  光伏节能项目建设风险实证评价

2.1 光伏节能项目建设评价指标体系

为进一步验证以上定量方法的可行性，以该单位参与的某广东光伏节能项目为例进行评价。而要评价，首先构建评价指标体系。而遵循独立性、全面性、可比性和效益性等原则，将评价指标构建如图1所示。

2.2 评价结果

2.2.1 权重确定

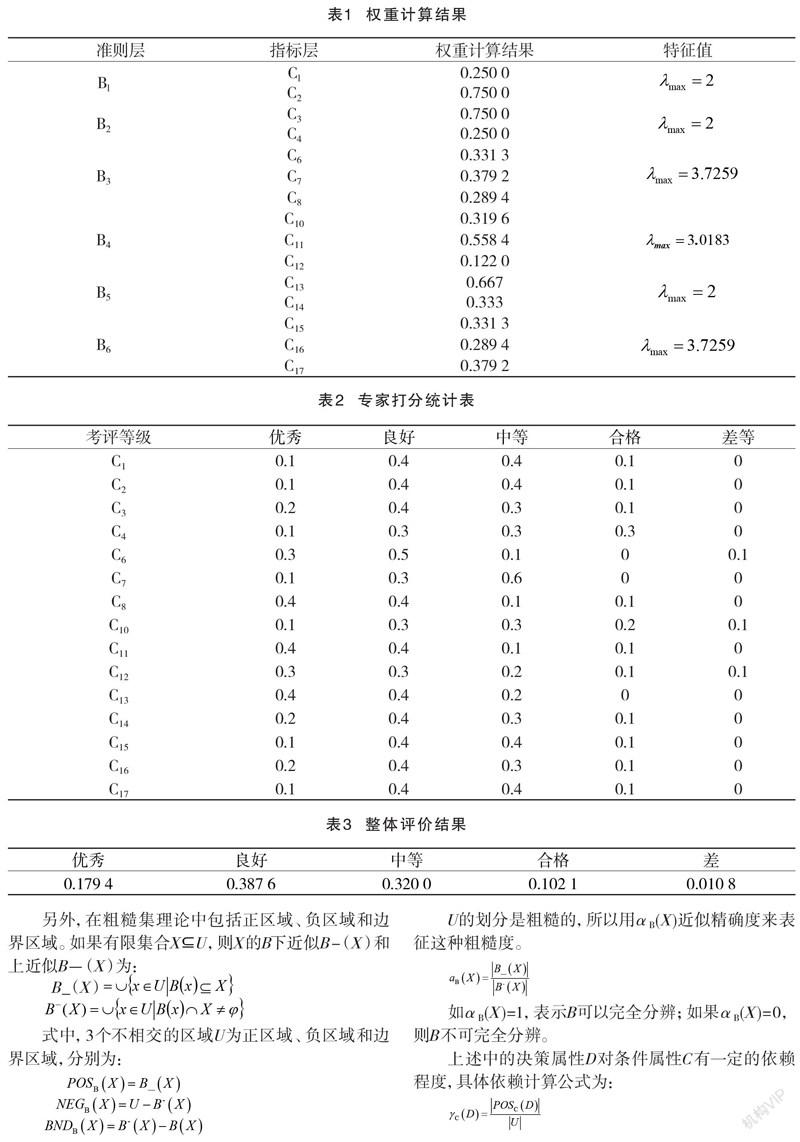
先确定权重。具体则是将专家打分数据录入到Matlab软件，从而计算得出权重，见表1。

2.2.2 评价结果

构建评价集V=（优秀，良好，中等，合格，差）=（90，80，70，60，50），邀请专家进行打分，并进行统计，从而得到表2。

根据表2构建判断矩阵进行计算，得到表3的整体评价结果。

2.3 最终评价得分

根据表3的评价结果，同时按照综合评价计算公式，可以得到最终的评价结果。具体则为：

P=0.1794×90+0.3876×80+0.3200×70+0.1021×60+0.0108×50=81.08

由此根据结果可知，该项目的综合得分为81.08，属于良好，即风险不大。

3  结语

综上，光伏节能项目受经济、技术、环境和政策等方面的影响，其自身发展会受到一定的限制，所以我国在光伏项目建设过程中，需要从各个方面进行思考，这样才能更好地实现项目风险的评估，最终减少公司自身建设的风险。

参考文献

[1] 魏鑫，李文甲，裴刚，等.基于光谱分频的太陽能光伏-甲烷重整互补发电系统[J].工程热物理学报，2019，40（3）：497-504.

[2] 周君明，张小松，孙博.太阳能溶液除湿空调系统再生技术的研究进展与能耗分析[J].制冷学报，2019，40（2）：154-160，166.

[3] 闫森，张义，鲍骏，等.基于CH3NH3PbI3钙钛矿量子点的荧光集光太阳能光伏器件[J].中国科学技术大学学报，2019，49（4）：290-296.

[4] 张哲旸，巨星，潘信宇，等.太阳能光伏–光热复合发电技术及其商业化应用[J].发电技术，2020，41（3）：220-230.

[5] 石磊，张福生，石军显，等.小型光伏的风险评估方法与模型[J].华北理工大学学报：自然科学版，2020，42（2）：94-100.

[6] 孙岩松，苏尤丽.农村分布式光伏发电投资风险分——基于蒙特卡洛模拟[J].河北北方学院学报：自然科学版，2020，36（3）：44-50.