基于卷积神经网络的闪存信道检测技术研究

胡海华，韩国军，张孝谊

（广东工业大学 信息工程学院，广东 广州 510000）

近年来，NAND 闪存已成为主流存储介质，在智能手机、个人电脑和大型数据中心中得到广泛应用[1-4]。随着制造工艺的进步，闪存单元的封装尺寸逐渐缩小。一方面，闪存单元中存储的比特数成倍增加；另一方面，闪存内部相邻单元寄生耦合电容效应变大，单元间干扰(cell-to-cell interference,CCI)增强，导致数据存储可靠性降低[5-6]。与此同时，编程次数和保持时间的增加引发随机电报噪声(random telegraph noise)和可持久性噪声(retention noise)，降低了闪存的使用寿命。

关于以上噪声带来的信道检测可靠性下降问题，国内外学者提出了一些解决方案[6-8]。针对单元间干扰，Peng 等[5]提出CSAD 和NIA-CSAD 检测策略；Dong 等[7]分析了单元间干扰信道模型，并用熵函数来近似求出两种状态分布重叠区的读取参考电压。上述工作需要估计出最优读取参考电压，该方法依赖闪存信道精准的先验信息(相邻单元先验信息、编程和擦除次数、保持时间等相关参数)。为减少对信道先验信息的依赖，文献[8]提出了循环神经网络(recurrent neural network,RNN)检测器。该检测器在未知信道先验信息下能减少噪声对信道可靠性的影响，但是该实验只分析了持久性噪声，没有考虑单元间干扰的影响，并且RNN 检测器复杂度较高，被激活会占用大量的系统空闲时间。在实际场景中，闪存信道会同时存在随机电报噪声、可持久性噪声和单元间干扰。信道噪声随保持时间变化，对阈值电压分布扭曲的影响是很难预测的。当前，深度学习技术迅速发展，在信道检测与估计中都表现出优越的性能[7-12]。本文提出的卷积神经网络(convolutional neural networks,CNN)可以从良好的数据集中学习闪存信道难以预测的变化，并能有效检测闪存单元状态。与现有的大多数检测技术相比，该方法不依赖于精确的信道模型。本文的贡献主要分为3 个方面:

1)通过相关文献对闪存信道特征的测试，可知相邻单元会受到编程单元的干扰[7-9]。基于闪存相邻单元间特征，本文先在二维坐标下分析了相邻单元编程后阈值电压的相关性，这种相关性表现为相邻单元阈值电压和受干扰单元阈值电压越大，受干扰单元阈值电压越往右偏移。文献[13]揭示了CNN 在相关噪声信道中表现出较好的特征提取效果，所以本文挑选CNN 网络来检测NAND闪存单元状态。

2)实验采用以随机电报噪声、可持久性噪声和单元间干扰为主要噪声源的闪存信道[9]，生成受干扰单元和相邻单元的阈值电压序列，组成二维训练数据集。低密度奇偶校验(low-density parity-check,LDPC)解码的单元状态通过独热编码数据预处理作为数据集标签。已训练好的CNN 检测器在没有任何信道先验信息下可以直接输出闪存信道的硬判决信息(单元存储状态)和软判决信息(闪存单元属于某种状态的后验概率)。假设信道模型已知，熵函数求解出电压分布相邻状态分布的重叠区间。在重叠区间中用穷举搜索法找到的最优阈值作为性能对比标杆，下面称之为最优阈值检测器(optimal threshold detector)。计算机仿真结果显示：本文提出的CNN 检测器与最优阈值检测器对比，在信道先验信息未知时，能有效提升闪存信道的检测性能。

3)与现有的RNN 检测器[8]相比，分析了两者的浮点运算数(floating-point operations,FLOPs)，单层CNN 网络复杂度显著小于单层RNN 网络。因此，CNN 检测器被激活所需的系统空闲时间比RNN 要少得多。

1 闪存信道系统

闪存信道系统模型如图1 所示，数据先通过擦除与编程操作写入闪存中，随后经过的干扰包括随机电报噪声、可持久性噪声和单元间干扰。

图1 MLC 闪存信道模型Fig.1 MLC flash channel model

1.1 编程操作

在NAND 闪存中，字线(word-line)由擦除状态单元和编程状态单元组成[14]。对于MLC 型的闪存单元，可以存储2 比特位，并将存储类型表示为4 个不同的状态：11、10、01 和00。11 是擦除状态，其余的是编程状态。

在编程之前，必须擦除闪存单元中的数据。擦除单元的阈值电压符合高斯分布[8]，该分布为

式中：σe和μe分别是被擦除单元阈值电压分布的标准差和平均值。

在编程操作中，闪存控制器会向浮栅注入一定量的电荷。编程状态的阈值电压也服从高斯分布[14]：

式中：σp和μp分别是被编程单元阈值电压分布的标准差和平均值。

1.2 随机电报噪声

编程和擦除次数会损坏浮栅晶体管隧道的氧化物，引起闪存单元阈值电压随机波动。因此，随机电报噪声采用类高斯分布建模为

1.3 可持久性噪声

可持久性噪声是由编程单元中电荷泄漏引起的阈值电压分布偏移。可持久性噪声遵循高斯分布[15]：

平均值μt和标准差σt由式(5)、(6)给出[16]：

式中：ΔVt为编程前后的闪存单元阈值电压变化；T为保持时间；PE 为编程和擦除循环次数；a0、at、At、Bt均为常数。

1.4 单元间干扰

单元间干扰是闪存信道中主要噪声之一[17]。编程单元阈值电压的变化会影响相邻单元的阈值电压。由单元间干扰引起的受干扰单元的总阈值电压影响强度计算公式为[17]

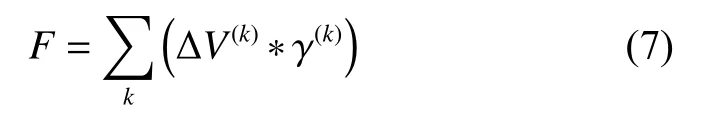
式中：ΔV(k)为第k个干扰单元的编程前后阈值电压偏移。如图2 所示，γ(k)干扰单元与干扰单元的耦合为受干扰单元与干扰单元的耦合比系数，γy表示垂直方向电容耦合系数，γxy表示对角线方向的电容耦合系数。对于不同的位线结构，用于计算F的干扰单元数目是不同的。为了简单起见，本文只考虑全位线结构,这种结构会降低被干扰单元受到的干扰强度。

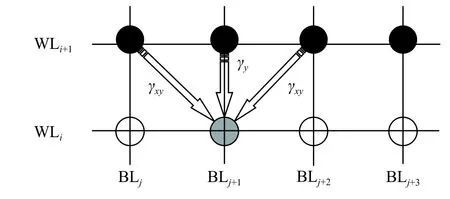
图2 多电平闪存的阵列结构Fig.2 MLC flash memory array structure

根据文献[17]，pc(k)(x)为单元间干扰的阈值电压分布。在随机电报噪声、单元间干扰和可持久性噪声的干扰下，阈值电压的条件概率分布函数为[18]：

式中：p(k)(x)表示k个状态的阈值电压分布，k∈{11,10,00,01}。为了统计出p(k)(x)，需要知道式(5)中保持时间T的大小，然而在实际场景中闪存控制器没有额外的存储空间来记录保持时间[19-20]。

参照文献[8-14]，MLC 闪存信道仿真参数的设置如下：μe=0.14，σe=0.25，at=0.62，a0=0.3，At=0.000035，Bt=0.000235，γy=0.08s，γxy=0.006s。s表示电容耦合强度。

2 CNN 检测器的设计

2.1 相关性

闪存信道参数设置为：PE 次数为1000，保持时间1 年，电容耦合强度s分别为0、1.4、2.5。由图3可以发现不同状态的受干扰单元不是交错呈现，而是与干扰单元的阈值电压具有正相关关系，随着耦合强度增大，受干扰单元的阈值电压向右偏移越明显。这现象显示了单元间的阈值电压具有相关性。当观测的干扰单元越多，这种相关性越明显，但是这种现象难以精确建立数学模型。

图3 闪存内部阈值电压相关性分析Fig.3 Schematic of the correlation analysis of the internal threshold voltage of flash memory

2.2 CNN 用于单元状态检测

本文的主要工作是将受干扰单元字线和干扰单元字线的阈值电压组成序列，输入到CNN 中进行提取特征，再输出闪存单元用于硬判决信息(单元存储状态)和软判决信息(闪存单元属于某种状态的后验概率)。

假设每个输入序列个数为M(字线长度)，每个向量为2 维，序列所有阈值电压向量在矩阵V∈R2×M中。

卷积层：本文挑选是一维卷积神经网络，输入序列表示为[V1V2…VM]矩阵，然后使用卷积核做卷积运算：

式中：I(1,j)是第一层CNN 第j个特征映射；k(1,j)为第j个卷积核；b(1,j)为网络偏置值，挑选的激活函数为整流线性函数(rectified linear unit,RELU)。下一层的卷积操作的输出为

式中：I(i,j)是第i层CNN 网络第j个特征映射；k(i,j)是第i层CNN 网络第j个卷积核。在本工作中卷积网络池化层会丢弃一些重要的特征信息，所以本文的卷积网络由过滤器和全连接组成，并且CNN 输出长度也为M。

假设有N个数据样本，对于输入样本i，经过CNN 网络提取特征后，形成序列Zi=[Zi1Zi2…ZiM]，希望输出每个序列节点所属某种类型的概率，即P(yim=j|Vim)。以MLC 为例，其有4 种状态，即j∈{VS11,VS10,VS00,VS01}，m∈{1,2,…,M}。Softmax 函数可以适用于多分类，其输出为

式中：k=4；θ1、θ2、θ3、θ4是Softmax 函数的权重参数；θ=[θ1θ2θ3θ4]。对于样本i中输入序列元素Vim，属于状态标签类型j的概率为

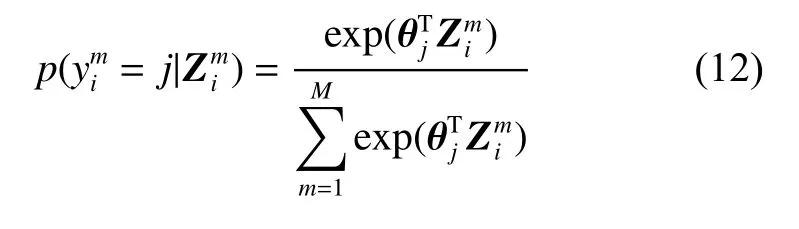
3 数据预处理

设计好CNN 检测器结构后，要对CNN 网络训练，则需要从本地获得训练数据。本文采用均匀量化策略获得闪存单元中的阈值电压数据。量化数量越多检测越精确，但是也会带来读取延迟。如表1，为了权衡闪存单元电压读取延迟和可靠性，选择64-level 均匀感知量化，在闪存单元状态的符号错误率(symbol error rate,SER)为0.0033时，读取延迟和可靠性折中。闪存控制器最小的读取单位是字线，则需要设置输入网络的序列长度与字线长度相当。

表1 不同量化区间的SER 结果Table 1 Simulation of SER in different quantization intervals

实验需要采集闪存控制器中读出闪存块中每个单元的量化阈值电压和LDPC 解码得到的每个单元状态信息。首先，感应和解码出若干组闪存块。其次，获得阈值电压V和状态标签x。其中，闪存单元的阈值电压在区间中被惑知，是第i个参考电压，则闪存单元的量化阈值电压V表示为

对于MLC 闪存单元有4 种不同的状态{VS11,VS10,VS00,VS01}，用独热编码预处理后为

对于字线上的闪存单元k，简单来说，当Softmax 函数输出的硬信息yk=[1 0 0 0]T时，单元k对应VS11；以此类推，当输出yk=[0 0 0 1]T，对应VS01。当输出软信息时，Softmax 函数输出每个单元属于各状态的概率，CNN 检测器能自适应地估计出字线中闪存单元状态概率，然后式(14)计算出对数似然比。闪存单元中的比特位bid对应的对数似然比(log-likelihood ratio,LLR)值可以被计算为

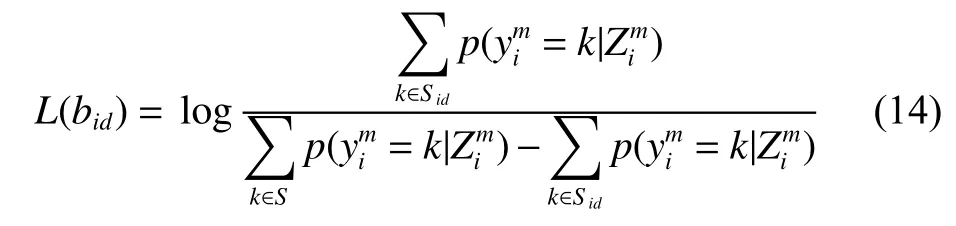
式中：Sid代表第i个闪存单元中第d比特位为1 的状态集。其中，S={VS11,VS10,VS00,VS01}，S1={VS11,VS10}，S2={VS11,VS01}。

4 实验仿真及分析

实验仿真在Window 10 操作系统下进行，采用Keras 深度学习框架。在训练网络之前，假设在实验中信道的保持时间未知，就需要生成失配的验证集来测试已训练好CNN 检测器的鲁棒性。定义失配时间公式为ΔT=Ttest−Ttrain，Ttrain和Ttest分别代表训练集和验证集的保持时间。定义失配编程和擦除循环次数公式为 ΔPE=PEtest−PEtrain，PEtrain和PEtest分代表训练集和验证集的编程和擦除循环次数。训练CNN 检测器步骤：

1)闪存控制器找到第i和第i+1 字线位置，即图2 中的WLi和WLi+1。

2)式(13)量化WLi和WLi+1中每个单元的感应电压。

3)LDPC 解码WLi中的信息，若解码成功，将独热编码预处理解码后的状态作为标签。若解码不成功，跳到下一个字线。返回1)，直到获取数据集数量满足实验要求。

4) 获取的数据集将用于训练CNN 检测器。为了提升训练效率，将数据集分成小批量数据，分批训练CNN 检测器。

CNN 结构由卷积核和特征图组成，可以表示为{L;f1,f2,…,fL;k1,k2,…,kL}。这里的L表示CNN 网络层数，f表示卷积核大小，k表示特征图数量。在实验中，通过比较误比特率(bit error rate,BER)和误帧率(frame error rate,FER)来评估系统性能。先进行单层CNN 和RNN 的复杂度分析，然后用表2 设置CNN 结构来测试在原始数据和编码数据下的系统性能。

表2 CNN 实验设置Table 2 CNN experimental setup

4.1 复杂度分析

对于文献[8]所提出的RNN 检测器，在实际的训练过程中会占用大量的时间，计算复杂度高。在理想条件下，通过设置CNN 和RNN 超参数使两者的复杂度相当，然后对比它们的性能。可是RNN 网络要比CNN 网络复杂多，在CNN 网络中有加法和乘法等线性运算，而RNN 网络中有许多的tanh 和exp 等复杂的非线性运算。为了方便比较，通过统计FLOPs 来衡量网络模型的复杂度。FLOPs 计算网络模型所有的加法和乘法次数。GRU 是RNN 网络模型中复杂度最低的网络模型。若设置一个层GRU 网络的神经元个数为L，输入数据的维度为D，N表示层数，序列为T。根据文献[21]，GRU 模型复杂度为

根据文献[22]，CNN 网络模型复杂度为

式中：Ci表示第i层输出数据的通道数；Ki表示第i层的卷积核大小；Ti为第i层输出的序列。在本文中C0=1，采用的二维阈值电压数据作为输入，则D1=2，K1=(D1,k)；用一层CNN 网络与一层GRU 网络对比复杂度，则C1=1，k为第一层卷积核尺寸。Softmax 函数复杂度可以忽略不计。此时，GRU 网络模型复杂度为，CNN 网络模型复杂度为O(4kT1)。如图4，设置实验环境s∈{1.4,1.6}，Ttrain=1 年，PEtrain=1000。图4展示了训练周期对误比特率的影响。CNN detector-1、CNN detector-2、RNN detector-1 和RNN detector-2 所标记的曲线对应参数k=1、k=2 和L1=1、L2=2 时的模型。随着训练周期变化，CNN 检测器和RNN 检测器趋于稳定。RNN 检测器性能亦可接近于CNN 检测器，式(15)中得到RNN 检测器复杂度与L1平方成正比。式(16)中CNN 检测器复杂度与K成正比。如果在有单元间干扰情况下要达到相同性能，CNN 检测器复杂度小于RNN检测器。

图4 不同训练周期下RNN 检测器和CNN 检测器比特错误率比较Fig.4 Comparison of the BERs of the RNN and CNN detectors under different training periods

为了避免GPU 等硬件带来的功耗等问题[8]，实验在无GPU 环境中进行。表3 是在无GPU 下参数FLOPs 和每个训练周期的耗时统计。随着参数的增加，RNN 检测器的FLOPs 接近倍数增加，带来的计算消耗和复杂度特别大。从耗时上可以看出，CNN 检测器训练周期相当于RNN 检测器训练周期的四分之一。MEI 提出在系统空闲时间时激活RNN 检测器，但是RNN 检测器训练耗时长[8]。与RNN 检测器相比，CNN 检测器被激活占用的系统空闲时间较短。

表3 CNN 检测器和RNN 检测器参数个数及FLOPsTable 3 Parameters and FLOPs of the CNN and RNN detectors

4.2 原始数据分析

为了更好验证模型检测有效性，LDPC 译码器尽可能收集解码后综合值为0 的码字数据。实验中选择最优阈值为性能对比标杆。最优阈值检测器通过熵函数得到两种状态分布的重叠区间，然后在重叠区间中找到最优读取参考电压。本文的CNN 检测器使用2 维数据输入网络。然后，测试了有无单元间干扰下两种检测器误码率对比，s=0 时，表示没有单元间干扰的信道；s=1.4 时，表示3 种噪声同时存在下的信道，并且单元干扰强度为1.4。

如图5 所示，在实验环境中有单元间干扰情况下匹配和失配的测试集(ΔPE=2500、5000)，Ttrain=1 年，CNN 检测器都取得很好的性能。当s=1.4 时，CNN 检测器跟最优阈值检测器比提升了闪存使用寿命。例如，在误比特率约为0.01，CNN 检测器可以将闪存编程和擦除循环次数提升大约11000 次，而最优阈值检测器仅在3000 次左右。在没有单元间干扰下，采用CNN 检测器性能增益较小，这时的噪声分布是标准AWGN 闪存信道，也是理想条件下的信道。此时，CNN 检测器与最优阈值检测器性能相似。由此，可以得出在有单元间干扰下，CNN 检测器能有效地提取出单元间干扰的特征来检测闪存单元状态，并且提升了闪存使用寿命。此外，当用到失配的测试集时，仿真性能对比结果显示，在失配编程和擦除循环次数小于5000 情况下，本文CNN 检测器检测性能也好于最优阈值检测器。

图5 失配编程和擦除循环次数比较Fig.5 Programming and erase cycles by mismatching data

传统保持低误比特率的方法是动态更新读取参考电压。然而在未知信道信息时，闪存控制器很难记录保持时间T。这时就很难通过传统方法获得新读取参考电压。前面的实验结果证明有单元干扰下，CNN 检测器优于最优阈值检测器，接下来实验通过对失配编程和擦除循环次数固定为ΔPE=1000，PEtrain=5000，测试CNN 检测器在失配保持时间下的性能。如图6，当时间不匹配到1 个月时，CNN 检测器还是优于最优阈值检测器的性能并且与保持时间匹配的数据接近。当保持时间失配增加到1 年时，初期CNN 检测器与匹配数据的性能略有下降。初期需要短周期更新CNN检测器适应信道变化，后期则可以数年更新一次CNN 检测器，就可以接近匹配数据的CNN 检测器误比特率性能，也证明了CNN 检测器鲁棒性强。

图6 失配保持时间比较Fig.6 Retention time through mismatching data

4.3 编码数据分析

为了分析CNN 检测器输出的软信息，实验选择了码率约0.889(2 048,2304)的LDPC 码写入到闪存单元中。在数据集中设置耦合强度因子为s=1.4，保持时间Ttrain=1 年和读写次数PEtrain=2000。为了避免验证数产生的读取延迟，实验减少了量化电压的数量，采用16-level 和32-level 两种均匀量化读取方法。CNN 检测器评估出闪存单元软信息，然后通过式(14)计算出LLR 值。图7 给出了本文提出方法与传统方法计算LLR 的系统性能比较。首先，设置0～20 最大迭代次数不等。其次，将CNN 检测器测试的失配保持时间ΔT=5月，失配编程和擦除循环次数 ΔPE=2 000。本文提出方法比5 月之前的传统方法计算LLR 收敛快。也就是说，CNN 检测器评估的LLR 更可靠，有助于置信传播(belief propagation,BP)算法[23-24]纠错性能的提升。

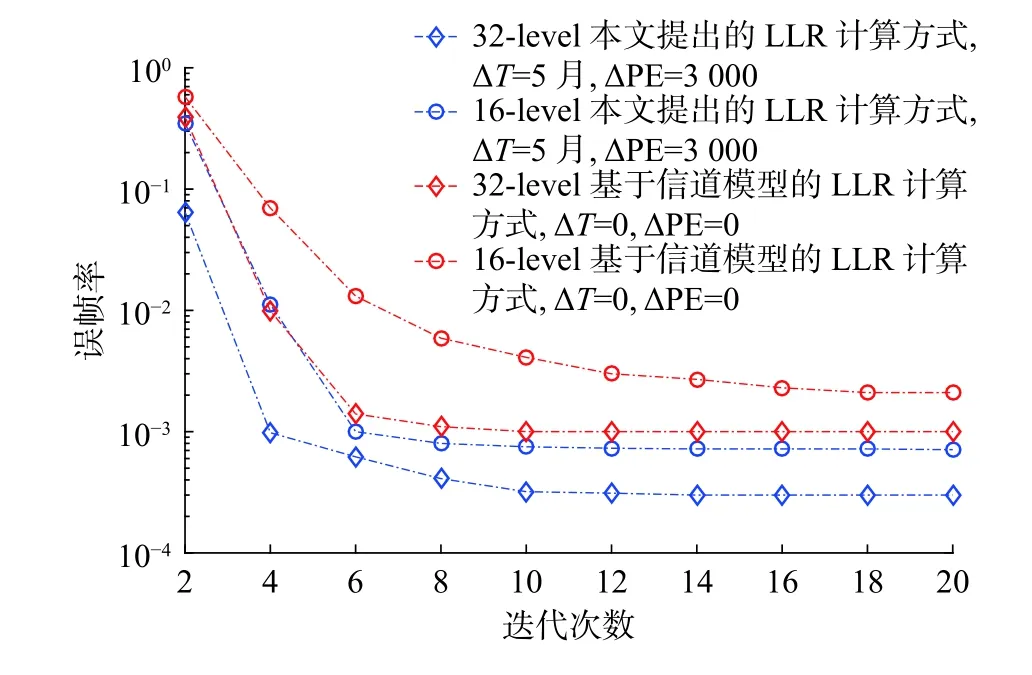
图7 最大迭代次数比较Fig.7 Comparison of maximum iterations

5 结束语

针对NAND 闪存存储数据可靠性下降的问题，本文提出CNN 检测器，该检测器不依赖于信道先验信息，通过学习相邻单元阈值电压的相关特征，能有效检测NAND 闪存单元状态。CNN 检测器具有训练周期短、鲁棒性强等特点，能占用较少的系统空闲时间来适应信道变化。CNN 检测器还能输出更准确的LLR 信息，提升BP 译码算法的纠错性能。闪存信道检测在深度学习中可以看作分类问题，因此本文提出的方法也可以应用到TLC、QLC 闪存信道中。