改进小波阈值在红外热波无损检测中的应用

邹兰林，李念琼

〈无损检测〉

改进小波阈值在红外热波无损检测中的应用

邹兰林，李念琼

（武汉科技大学 汽车与交通工程学院，湖北 武汉 430065）

近二十年来红外热波无损检测技术迅速发展，并在较多领域都得到了普遍应用，但碍于其易受环境影响和工作元件不均匀的特殊性，非制冷红外热像仪原始热波图总存在一定程度的噪声污染，因此对原始热波图进行去噪处理是该技术的关键步骤。传统的改进小波阈值去噪方法局限于对阈值进行自适应分解尺度的改造，使阈值函数平滑连续保真。在噪声方差估计方面没有针对性的方法，而噪声的方差估计是阈值的关键变量，这决定了小波阈值去噪的效果。本文将根据红外图像噪声特性建立混合噪声模型，在噪声模型的基础上进行噪声方差估计、改进阈值及阈值函数，通过软件获取最佳函数参数，最后对仿真模拟结果进行分析，对真实图像进行处理评价，结果表明经改进后的小波阈值去噪方法相对于传统阈值去噪方法和部分滤波去噪方法具有更好的去噪效果。

小波阈值；红外无损检测；仿真模拟；噪声建模

0 引言

随着国家对检测精度和检测损伤程度的要求越来越高，红外热波无损检测技术逐渐出现在人们的视野中[1]，其主要通过热源对损伤部位进行主动加热，缺陷部位会因为比其他部位的导热能力差或隔热在红外热像仪中显示出不同的热波序列图。它拥有检测速度快、对试件几乎没有损害、检测结果直观明了等优点，目前已经普遍应用于交通、军工和新能源领域。然而，红外热像仪的读取、传输和储存容易受外界条件和试件本身不均匀性的干扰，这使得原始热波图像信噪比低、噪声构成复杂，对后续的主观分析评价造成了巨大的影响，使得检测效果和效率都大幅度降低。因此，如何对原始热波图像进行去噪，提高其信噪比，突出图像细节，提高检测效率是红外热波无损检测技术的关键研究内容[2]。

红外图像中的混合噪声（随机和条纹噪声）构成复杂，很难被传统去噪方法去除[3]。与传统去噪方法相比较，利用小波分析去噪方法则显得相对更能抓住噪声的本质特性。在利用小波分析的许多去噪方法当中，比较常用的是小波阈值去噪法，这是由于它的多分辨率分析的特性，能够较好地保留图像边缘信息，算法运算量相对较小，运行的速度较快，并且所具有的多尺度、多方向、时频局部化的特点，可以精确对信号定位，对噪声进行抑制，从而使图像的质量提高。

近些年来，学者们逐渐将小波阈值去噪应用至红外图像去噪[3]，主要工作有：对阈值进行改进，使其能够自适应分解尺度，对阈值函数进行改进，使其获取的小波系数连续且保真。这些改进均在处理已知噪声方差的白噪声上取得了不错的效果，却缺乏对复杂噪声的适应性，本论文通过建立红外图像噪声模型，分析其噪声特性，建立随机噪声与固定噪声协方差矩阵获取噪声方差，改进阈值与阈值函数，通过软件实现对阈值函数控制因子最佳值的获取，最后通过仿真模拟与传统方法进行去噪效果比较，综合对处理后图像的主观分析和客观评价指标，得到改进后的阈值与阈值函数对复杂噪声具有更好去噪效果的结论。

1 噪声建模

建立红外图像噪声模型是去除红外图像噪声的关键。红外图像的信息与噪声的比例比传统图像低，并且噪声构成比较复杂，外界环境的干扰和内部元件的成像特性都能产生多种噪声，由此使噪声建模变得更加困难。本文将红外图像噪声分为两类：随机噪声和固定噪声。

通过随机噪声和固定噪声的特性，将噪声模型建立为3D模式，将噪声的信息通过三维形式表现出来，三维信息分别代表空间坐标和时间坐标。这种处理方式将复杂的三维噪声分解成了若干个简单的一维或者二维噪声的集合，简化了噪声模型[4]。

3D噪声模型表达式为：

TVH＝＋TVH＋VH＋TH＋TV＋H＋V＋T(1)

式中：T代表时间；V代表垂直方向的信息；H代表水平方向的信息；S是所有像素点的平均值。

1.1 红外图像随机噪声

随机噪声，顾名思义其空域和时域坐标均为随机的噪声。表现为位置不固定的噪点，它主要由红外图像本身背景辐射的光子起伏，读取和转换电路以及输出电路的附加噪声构成。我们认为高斯噪声和泊松噪声组成了随机噪声。这两种信号的强度与信号本身的平均强度相关。

由3D噪声模型可知，如果客观条件不变，即红外热像仪和拍摄背景不变，空间分量就不会产生变化，那么通过对1s内视频中的25帧进行帧相减、平均，余下的部分就是这1s内的随机噪声。

通过软件编程，对某红外视频进行差分，进行帧相减获取随机噪声的结果见图1。

图1 随机噪声和添加随机噪声后的图像

1.2 红外图像固定噪声

固定噪声，表示在同一个位置和多个位置固定出现的噪声。它是由红外热像仪检测元件本身的响应程度不统一、成像缺陷和其他波段影响造成的。红外图像固定噪声由图像的非均匀性和图像盲元组成，非均匀性就是使图像模糊不清的条纹噪声，盲元即是椒盐噪声。

1.2.1 非均匀性模型

物体通过红外热像仪探测元件映射至内部的响应模式可以分为线性和非线性，通常情况下我们认为其呈线性[5]。因此，本论文的响应模式表示如下：

R,k＝a×E,k＋(2)

式中：,表示像素的空域坐标，＝1～，＝1～，和分别表示图像的行宽和列宽；E,k和R,k分别表示实际辐射值和经探测元映射后的辐射值。a和b分别为此模型的线性指数和常数偏移，a服从均值为1，方差为的高斯分布。偏移b服从均值为0，方差为的高斯分布。

通过软件生成满足上述条件的线性系数和偏移值，然后根据线性响应的非均匀性模型使清晰图像产生非均匀性。添加非均匀性后的图像如图2所示：其中图(a)为红外图像，图(b)为产生非均匀性后的红外图像，＝0.01,＝5。

图2 添加非均匀性的前后图像

1.2.2 椒盐噪声

目前普遍采用的基础理论认为盲元在红外图像中的表现形式与普通图像中的椒盐噪声类似。因此将红外图像中的盲元当作椒盐噪声处理生成，其概率分布密度为：

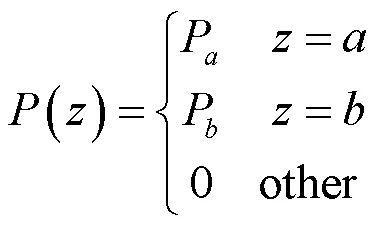
若＞，灰度值为的点在图像中将显示为一个亮点，灰度值为的点在图像中将显示为一个暗点。通常将，设置为图像的极大极小值。P和P为椒盐噪点的概率密度分布。

由于红外热像仪中自带了盲元算法，其采集到的红外图像中几乎不存在盲元，因此本论文忽略了盲元对图像的影响，最终生成的红外图像噪声模型如图3所示。

图3 生成的总噪声

2 小波阈值

小波阈值去噪方法原理简单、容易实现、去噪效果良好，已经在各去噪处理中得到了广泛应用。但是传统的小波阈值去噪方法具有一定的缺陷，传统阈值不能够自适应小波分解的尺度，使得每层的阈值单一，去噪效果受到限制。传统阈值函数获得的小波系数不够保真或者不连续，这增加了小波去噪和重构的难度，降低了去噪效果[6]。近些年来，学者们对如何改进阈值，使其能够自适应分解尺度，如何改进阈值函数，使其平滑连续且保真，进行了大量的研究，也获得了去噪效果良好的阈值及阈值函数，却忽略了影响小波阈值去噪效果的关键因素：噪声方差。本论文在改进阈值及阈值函数的基础上，进一步针对前文构造的红外图像噪声模型进行噪声方差估计。

2.1 小波阈值去噪原理

对含噪声的信号使用选用小波进行分解，噪声信号的小波系数偏小，信号的小波系数偏大，因此设定一个阈值来筛选信号，滤除噪声，而后再通过小波逆变换重构信号图像[7]。

设信号模型为()＝()＋()，其中，()是原信号，()是方差为2的高斯白噪声。

以上述信号为例。平均采取信号的若干点，()，＝0, 1, …,－1，则()小波变换系数为：

在实际应用中，难以直接对式(4)进行实现，并且在大多数情况下()没有表达式。但是它可以通过下面两个公式来递归实现：

S(＋1,)＝S(,)×(,) (5)

W(＋1,)＝S(,)×(,) (6)

式中：和为滤波器，用于滤除低频和高频信号；S(0,)为原始信号()，S(,)为近似的函数；W(,)则为小波系数。那么，经变换重构后的小波可以表示为如下形式：

将小波系数W(,)简记为,k，对()＝()＋()作小波分解后，小波系数,k仍然由两部分组成，分别是真实信号()对应的小波系数W(,)，记为u,k，白噪声()对应的小波系数W(,)，记为v,k，那么有：

,k＝u,k＋v,k(8)

小波阈值去噪方法过程如图4。

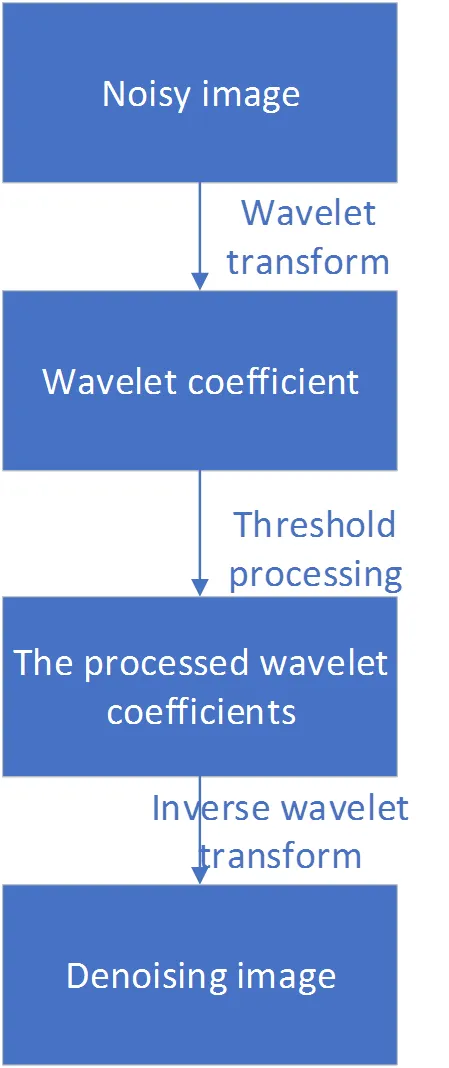
图4 小波阈值去噪流程图

2.2 噪声的方差估计

噪声的方差估计决定了阈值的准确性，它决定了去噪效果的好坏，传统的噪声方差估计适用于单一的加性白噪声，对于噪声复杂的红外图像噪声难以适应，本论文建立非均匀性与随机噪声的混合模型。对于×的图像块，将其整理为(×)×1的列向量y,k：

y,k＝x,k＋n,k(9)

式中：x,k为干净的图像块；n,k为混合噪声，其均值为零向量。协方差矩阵为：

＝r2＋s2(10)

式中：为2×2单位矩阵；为2×2的特殊对角矩阵：

式中：1为×元素均为1的方阵；0为×元素均为0的方阵。

此方法构造了混合噪声的协方差矩阵，分别求得随机噪声强度r和非均匀性导致的条纹噪声强度s即可获取混合噪声强度：

r＝MAD(HH) (11)

式中：HH为图像一阶小波分解中的对角高频分量。MAD为绝对中位差，其表达式为：

MAD()＝1.4726×median(|－median()|) (12)

经过小波分解后的对角高频分量中不包含有着垂直或者水平特性的条纹噪声，因此使用此方法很好地消除了固定噪声对随机噪声方差估计的影响。

本论文采用文献[8]的方法，利用各方向的差分图来消除固定噪声的方向特性。对含噪声图像分别做不同方向的一阶差分，得到两幅梯度图Ñ和Ñ。固定噪声方差的估计为：

2.3 小波阈值改进

2.3.1 阈值改进

针对通用阈值不能自适应分解尺度的不足，本论文在通用阈值的基础上添加尺度控制因子，改进后的阈值能够自适应分解尺度，随着分解尺度增大阈值逐渐减小，更符合小波系数在各层分解的情况：

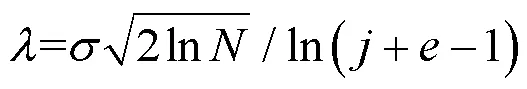
式中：是噪声的总方差；是信号的尺寸。

经改进后的阈值克服了传统固定阈值不能随分解尺度改变的缺点，更贴合了每层噪声信号经小波分解后的临界值，减轻了对信号小波系数的过度扼杀，增强了小波阈值去噪方法的效果。

2.3.2 阈值函数改进

传统的硬阈值和软阈值存在着获取的小波系数失真、不连续等缺点[9]，为了降低这些缺点对去噪效果造成的影响本论文设计了如下阈值函数，表达式：

3 仿真模拟

3.1 参数设置

本论文基于软件平台，对图像添加随机噪声和固定噪声，对加噪后的图像进行多尺度的分解，提取各尺度上的高频系数，对其进行相应的阈值处理，最后将处理后的新小波系数进行重构后得到去噪后的图像。

以0.1为间隔，在软件平台上从0到10对、进行赋值，以峰值信噪比为评价标准，选取了＝0.3和＝2.5作为这两个参数的值。

由于小波函数众多，分解层数也是自由选取的，所以本论文所期望的实验效果也会不尽相同。理论上讲，小波分解层数越高，重构得到的图像就会越清晰，但是相应的重构图像的难度就会越大，本论文选取sym4小波，3层分解尺度为实验基础。

3.2 结果分析

对添加噪声后的图像使用不同方法进行处理后的结果如图5所示。

图5 仿真图像不同去噪方法处理结果

从效果比较图中可以看出，硬阈值函数去噪方法处理后图像的视觉效果是其中最差的，不管是其细节部分还是其相对平滑部分都显得有些模糊，软阈值函数去噪方法处理后的图像虽然整体显得没那么多噪声存在，但是图像的细节信息也没能保留，传统中值滤波去噪方法并不能很好地去除噪声，虽然较好地保留了图像的细节信息，但是对于图像的非均匀性和图像的随机噪声没有得到有效的处理。改造后阈值函数去噪方法较好地解决了图像的非均匀性，图像的随机噪声和椒盐噪声也得到了较好的滤除。

3.3 客观指标评价

均方误差（mean square error，MSE）、峰值信噪比（peak signal to noise ratio，PSNR）和结构相似性（structural similarity，SSIM）是传统的客观评价标准。去噪后求得的均方误差越小、峰值信噪比越大，说明图像的清晰度越高。SSIM取值范围是[0, 1]，SSIM的值越大，表示去噪图像与原图像越相似。其表达式分别为[10]：

式中：(,)为原始图像在(,)坐标上的像素大小；(,)为去噪后的图像在(,)位置上的像素值；代表图像的行数；代表图像的列数。

结构相似性的值度量了处理后的图像与原图像的相似程度，它分别从亮度、对比度和结构三个

方面来对图像进行考量。

式中：和分别表示图像和图像的均值；和分别表示图像和图像的方差；表示图像和图像的协方差；1，2和3是常数。

为了更好地对比改进阈值函数去噪方法与传统方法的去噪效果，本论文采用了上述指标作为客观评价标准，结果如表1所示。

从表1中的数据可以看出，上文提到的几种阈值函数和传统中值滤波和本论文改进的阈值函数在对图像进行去噪后，均方误差大致相同，用硬阈值函数进行去噪时，其PSNR最小，所以可得出硬阈值的去噪效果最差；改进阈值函数的PSNR最大，去噪效果最好，结构相似性方面，改进后的阈值函数也脱颖而出，经改进阈值函数处理后的图像更接近原始图像，因此具有更好的去噪效果。

3.4 真实图像处理

为了验证仿真模拟的结果，本论文采用几种成熟的滤波去噪方法和改进小波阈值去噪方法对真实非制冷红外热像仪进行了去噪处理，处理结果如图6所示。

表1 仿真模拟图像几种去噪方法评价指标对比

与现在较为成熟的几种滤波去噪[11]方法相比。双边滤波和保边滤波没有能够很好地滤除条纹噪声，超级滤波虽然很好地滤除了条纹噪声，但细节模糊严重。复合引导滤波效果最好，在滤除噪声的同时较好地保留了图像细节，本论文的改进小波阈值去噪方法相对于处理仿真图像，对真实非制冷红外热像仪图像的处理有更好的效果，真实图像由非均匀性产生的固定条纹噪声相对于仿真模拟的条纹噪声更好地被去除，图像细节部分保留较为完整。

综合对去噪后仿真模拟图像与真实图像的直观评价和去噪后仿真模拟图像评价指标数据对比，能够得出结论，本论文改进后的阈值函数对于非制冷红外热像仪采集到的红外图像噪声相对于传统阈值方法及部分成熟应用于去噪的滤波方法具有更好的去噪效果。

4 结语

在红外热波无损检测中，非制冷红外热像仪采集的原始热波图像的信噪比低、噪声构成复杂是影响人们对结果进行分析判断的主要原因，对红外图像进行去噪是红外热波无损检测的重要工作。如何将小波阈值去噪方法合理地应用至红外图像去噪是近年来学者们研究的热点，本论文不同于前人单一的处理高斯白噪声，建立了更完整的红外图像噪声模型，增添了非均匀性引起的条纹噪声，基于噪声模型对噪声方差进行了估计，改进了阈值和阈值函数，通过软件编程，获取了阈值函数的最佳参数，最后通过仿真模拟和真实数据实验对不同方法的去噪效果进行了评价，结果表明，改进后的阈值和阈值函数对加噪图像有更好的去噪效果，图像细节也更加还原。

[1] 陈大鹏, 毛宏霞, 肖志河. 红外热成像无损检测技术现状及发展[J]. 计算机测量与控制, 2016, 24(4): 1-6.

CHEN Dapeng, MAO Hongxia, XIAO Zhihe. Infrared thermography NDT and its development[J]., 2016, 24(4): 1-6.

[2] 江海军, 陈力. 闪光灯热激励红外热波成像无损检测设备及应用[J]. 无损检测, 2017, 9(12): 20-22.

JIANG Haijun, CHEN Li. Application of flash thermal excitation infrared thermographic nondestructive testing equipment[J]., 2016, 24(4): 1-6.

[3] 张小燕, 吐尔洪江·阿布都克力木. 小波变换的阈值图像去噪算法改进[J]. 计算机技术与发展, 2017(3): 81-84.

ZHANG Xiaoyan, Turghunjan ABDUKIRIM TURKI. Improvement of threshold image denoising algorithm with wavelet transform[J]., 2017(3): 81-84.

[4] 唐麟, 刘琳, 苏君红. 红外图像噪声建模及仿真研究[J]. 红外技术, 2014, 36(7): 542-548.

TANG Lin, LIU Lin, SU Junhong. Modeling and simulation research of infrared image noise[J]., 2014, 36(7): 542-548.

[5] 张盛伟, 向伟, 赵耀宏. 基于引导滤波的红外图像条纹噪声去除方法[J]. 计算机辅助设计与图形学学报, 2017, 29(8): 1434-1443.

ZHANG Shengwei, XIANG Wei, ZHAO Yaohong. Stripe noise removal method for infrared images based on guided filtering[J]., 2017, 29(8): 1434-1443.

[6] 杨鑫蕊. 改进的小波阈值去噪算法研究[D]. 哈尔滨: 哈尔滨理工大学, 2014.

YANG Xinrui. The study on improved wavelet threshold denoising method[D]. Harbin: Harbin University of Science and Technology, 2014.

[7] 王风. 小波变换在图像去噪及增强中的应用研究[D]. 淮南: 安徽理工大学, 2020.

WANG Feng. Application of wavelet transform in image denoising and enhancement[D]. Huainan: Anhui University of science and Technology, 2020.

[8] 李方舟, 赵耀宏, 向伟, 等. 基于改进非局部均值的红外图像混合噪声去除方法[J]. 红外与激光工程, 2019(1): 169-179.

LI Fangzhou, ZHAO Yaohong, XIANG Wei, et al. Infrared image mixed noise removal method based on improved NL-means[J].2019(1): 169-179.

[9] 姚雪晴. 基于小波域分频的变电站红外监控图像噪声自适应滤波算法[J]. 电工技术, 2017(5): 26-27, 172.

YAO Xueqing. Adaptive filtering algorithm for substation infrared monitoring image noise based on frequency division in wavelet domain[J]., 2017(5): 26-27, 172.

[10] 钱伟. 红外与可见光图像融合方法与评价指标研究[D]. 银川: 北方民族大学, 2018.

QIAN Wei. Infrared and visible image fusion methods and evaluation indexes research[D]. Yinchuan: North Minzu University, 2018.

[11] 乔玉雷. 基于Morlet小波分频的保边滤波去噪方法[J]. 石油物探, 2011, 50(2): 139-143, 154.

QIAO Yulei. Boundary-preserving filtering denoising method based on frequency division of Morlet wavelet[J]., 2011, 50(2): 139-143, 154.

Application of Improved Wavelet Threshold in Infrared Thermal Wave Nondestructive Testing

ZOU Lanlin，LI Nianqiong

(,,,430065,)

Infrared thermal wave non-destructive testing is a new type of technology that has developed rapidly in the past two decades and is widely used in many fields. However, owing to its vulnerability to influence from environmental factors and the particularity of itsuneven working components, there is always a certain degree of noise pollution in the original thermal image of uncooled thermal imaging cameras; therefore, denoising the original thermal image is a key step in this technology. The traditional improved wavelet threshold denoising method is limited to the transformation of the adaptive decomposition scale of the threshold, such that the threshold function is smooth and continuous. There is no targeted method for noise variance estimation, which is the key variable of the threshold that determines the effect of wavelet threshold denoising. This study establishes a mixed noise model based on the noise characteristics of infrared images, estimates the noise variance, improves the threshold and threshold function based on the noise model, obtains the best function parameters through software, and finally analyzes the simulation results, process, and evaluation of real images. The results show that the improved wavelet threshold denoising method has a better denoising effect than the traditional threshold denoising method and partial filter denoising method.

wavelet threshold, infrared non-destructive testing, simulation, noise modeling

TP751.1

A

1001-8891(2021)11-1089-08

2021-05-31；

2021-09-13.

邹兰林（1974-），男，湖北武汉人，副教授，博士，研究方向为桥梁检测。E-mail：147461632@qq.com。

国家重大科研仪器研制项目（51827812）；国家自然科学基金项目（51578430，51778509）。