基于频域变换的MEMS声学薄膜缺陷检测算法

魏 冬，桑 梅，禹敏慧，黄耀慷，刘红光，刘铁根

（1.天津大学 精密仪器与光电子工程学院，天津 300072；2.天津大学 光电信息技术教育部重点实验室，天津 300072；3.天津市计量监督检测科学研究院，天津 300192）

引言

微机电系统（micro-electro-mechanical system，MEMS）是集合了微电子技术、机械技术和声学等多学科的高科技传感系统[1]，已经在航天、通讯等领域获得了广泛的应用[2]。由于MEMS 结构多样、尺寸微小且生产工序复杂，对流片、储存和封装环境要求极高，通常在流片工序完成之后，晶圆表面会留下许多表面缺陷，如斑块、裂纹等，必须对其进行检测以保证产品质量。当晶圆到达器件厂商一方，为保证MEMS 器件的质量和性能，在切分、封装前后还需要进行颗粒、污染等因素的检测。传统的MEMS 表面缺陷检测方法（光电检测、涡流探伤和高分辨率X 射线衍射HRXRD）对检测设备要求极高且有可能对微构件造成二次损伤。机器视觉检测技术作为一种涉及光学、计算机技术和图像处理的多领域交叉综合性技术，因其具有无接触、高精度的优点，对于提高MEMS微构件的制造水平，降低生产成本具有重要的研究意义和实用价值[3]。MEMS声学薄膜是新型耳机和麦克风中的核心器件，它是声（机械振动）/电（电压、电流）信号相互转换的重要执行器件。由于其尺寸微小且对外部环境要求高，空气中悬浮的水蒸气、纤维、灰尘等杂质都可能以表面缺陷的形式附着在声学薄膜表面，并对其振动模态产生负面影响。

声学薄膜缺陷图像的特点是在周期性结构纹理的背景中叠加着一些斑块状和条带状杂质，对于这种缺陷进行检测时，背景信息往往会造成一定的干扰，不利于缺陷区域信息的提取。近年来研究者们提出了很多表面缺陷检测算法[4]，大致可分为依赖无缺陷模板图像的参考法[5]和不依赖于模板的非参考法[6]。参考法的性能会受到图像旋转、缩放和不均匀照明条件造成的图像扭曲等因素的影响，在图像差影计算后会产生许多噪声，稳定性较差[7]。非参考法中通常利用傅里叶变换[8-9]、小波变换[10]和Gabor 变换[11-12]等分析方法将二维图像信号转换到频域，根据相关的频率分布准则提取背景的纹理特征。这类方法能够结合背景纹理的频域特性和空域特性进行研究，在非参考法中针对周期性结构的应用效果最好。Gabor变换虽然符合人类视觉感受特性，具有较好的方位选择性，但参数的计算量较大[13]，不满足快速检测的需求。

本文提出了一种结合二维离散傅里叶变换（DFT）和Haar 小波分解的MEMS声学薄膜缺陷检测算法，主要包含3 个步骤：1）通过DFT 得到缺陷图像的傅里叶频谱图，采用布尔掩码消除频域中周期性结构对应的主频分量，对剩余的频谱图采用二维离散傅里叶逆变换（IDFT）获得包含缺陷信息的重构图像；2）对缺陷图像进行单层Haar 小波分解去噪，得到低频分量子图像A，体现了缺陷图像的主要表现力，能够较为清晰地显示缺陷的形貌；3）采用阈值法针对低频分量子图像进行二值化图像分割以进行缺陷的提取。算法流程如图1所示。

图1 算法流程图Fig.1 Flow chart of algorithm

1 周期性结构的背景纹理去除

1.1 傅里叶频谱分析

傅里叶频谱对于灰度图像中的周期性结构纹理具有很好的适用性。对于只包含有周期信号的无缺陷图像来说（见图2（a）），其频谱由规则分布的一系列谐波频率点所组成，表现在含有缺陷图像的频谱中（见图2（b））为一系列突出的规则峰值。通过将这些峰值及其相邻的峰值修正为0，就能够有效地去除周期性模式。通过设置特定角度对频谱进行扫描，能够发现含缺陷图像频谱的频率分量相较于无缺陷图像的频谱具有更陡峭的尖锐峰值，即对应更大的梯度值[14]。因此可以计算频谱的梯度分布并从频谱中提取周期性结构的相关频率分量。

图2 示例图像及其频谱梯度图Fig.2 Sample diagrams and spectrum gradient diagrams

缺陷图像f(x,y)看作是缺陷区域fd(x,y)和背景纹理区域fp(x,y)两部分的信息之和：

1.2 周期性背景纹理的去除

重构之后的图像如图3所示。无缺陷图像样本中的大部分背景纹理都被去除，而有缺陷图像样本中则留下了较为完整的缺陷区域信息，证明了本方法的有效性。上述算法的流程如图4所示。

图3 IDFT 重构图像Fig.3 Reconstructed images by IDFT

图4 去除周期性结构纹理流程图Fig.4 Flow chart of removing periodic structure texture

2 傅里叶逆变换重构图像的缺陷分割

2.1 单层Haar 小波变换去噪

由图3所示，在重构图像中仍存在部分噪声。经过分析和统计，MEMS声学薄膜表面缺陷图像的频谱图特点是：缺陷信息处在低频部分，而高频区域主要包含噪声，因此可以采用低通滤波器进行去噪处理。对于二维图像信号来说，分别在水平和垂直方向进行滤波能够实现二维小波的多分辨率分解，得到多子带图像。图5 为进行二维离散小波变换后的子图像分解示意图。L 表示低通小波滤波器，H 表示高通小波滤波器。LL、HL、LH和HH 表示在水平和垂直方向上采用相应的小波滤波器进行卷积后得到的小波系数，分别对应原图像的近似值、原图像在水平方向的特性（水平子带）、原图像在垂直方向的特性（垂直子带）和原图像的对角特性（对角子带）。

图5 小波变换子图像分解示意图Fig.5 Schematic diagram of wavelet transform sub-image decomposition

将傅里叶重构后的图像进行Haar 单层小波分解，得到A、H、V、D4 幅子图像，其尺寸变为重构图像的一半。A对应于原始图像的近似值，其他3 个子带H、V和D对应于水平、垂直和对角线方向的小波系数。二维图像的Harr 小波变换如下所示：

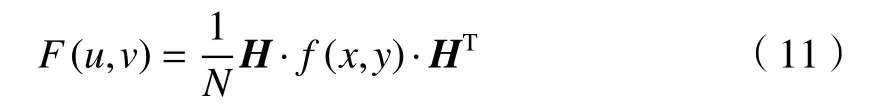
式中：H为Haar 变换矩阵；N为阶数。经过小波滤波后的图像如图6所示。

图6 Haar 单层小波分解子图像Fig.6 Sub-image of Haar single-layer wavelet decomposition

2.2 去噪图像二值化

为了分割出缺陷区域，需要对近似值图像进行二值化操作。从图6（a）中可以看到，重构图像的缺陷区域灰度值分布均一且与背景部分具有较大的差异，可按照如下规则进行二值化操作：

式中：μd为图像的均值；σd为图像的方差；td为控制常数。通过二值化操作，使得重构图像中的缺陷部 分能够被较为完整地分割（如图7所示）。

图7 去噪图像二值化结果图Fig.7 Binaryzation result diagrams of denoising image

3 实验和讨论

本文以一组真实的MEMS声学薄膜的缺陷图像为实验样本，对算法的有效性进行验证。实验使用的硬件环境为搭载Intel Core i7-CPU@2.60 GHz 以及RAM 为8.0 GB 的计算机，操作系统为Windows10，算法编程软件为MATLAB。

3.1 缩放常数 tg对周期性纹理去除的影响

缩放常数tg主要用于限制通过OTSU 算法得到的分割阈值Tg，它的取值会影响到布尔掩码的生成，进而对背景纹理的去除效果产生影响。图8 给出了tg=0.5、 0.7、1 .0、1 .5时不同缺陷图像的重构效果。当tg的值过大时，缺陷重构图像中还残留有未去除的周期性结构纹理，原因是傅里叶频谱中仍存在一部分对应于背景纹理的高频分量并未被去除；当tg的值过小时，有可能会导致一部分缺陷信息的频率分量被删除，使得缺陷区域信息减少并出现噪声，影响重构效果，因此，可以将tg的取值范围定在0.7 ∼1.0。

图8 放射状缺陷图像背景纹理去除效果图Fig.8 Removal effect diagrams of background texture for radial defect images

3.2 算法对不同种类MEMS声学薄膜检测的适用性

为验证本算法对于消除不同周期性结构纹理的适用性，选择2 种背景纹理的MEMS声学薄膜缺陷图像导入本算法进行缺陷检测，其重构图像和二值化结果如图9 和图10所示。可以看到，算法对于周期性结构纹理的去除效果较好，缺陷区域得到较为完整地保留，并且当成像质量较高时，图像的相关细节较为清晰，分割效果得到进一步提升。然而，当缺陷区域的面积较大时，在重构图像中缺陷的周围会产生波纹状的噪声。从前文中的频谱能够看出缺陷区域的信息主要集中在频谱中的低频部分，周期性结构纹理的信息主要集中于高频部分。对频谱的操作会使得二者之间连接区域的频率分量产生缺失进而出现噪声。但经过小波分解和二值化处理后这些噪声也得到了去除，对最终的二值化结果并未产生影响。

图9 XC-29 声学薄膜缺陷检测图Fig.9 Defect detection diagrams of XC-29 acoustic film

图10 XC-25 声学薄膜缺陷检测图Fig.10 Defect detection diagrams of XC-25 acoustic film

4 结论

本文提出了一种无监督的MEMS声学薄膜缺陷检测算法，通过提取频谱梯度图中高梯度值对应的频率分量以消除周期性背景纹理，对重构图像进行单层Haar 小波变换得到去噪后的低频子图像，并通过阈值分割输出了二值化缺陷图像。实验结果表明，缩放常数tg取值于0.7～1.0 时较为合理，存在于不同背景纹理的缺陷信息也能够被成功检测，证实了本算法能够较好地完成具有周期性结构纹理的MEMS声学薄膜表面缺陷检测任务。