玄武岩柱状节理六边形结构形成机制探讨

周思耘，吴晨

1)北京航空航天大学物理学院，北京，102206；2)中国科学院青藏高原研究所，北京，100101

内容提要:玄武岩柱状节理往往呈现完美的六边形石柱，这种现象引起了人们的广泛关注和好奇，但是对于其形成机理尚无合理的解释。本文通过对冷却过程中的玄武岩进行受力分析，提出当岩石(浆)冷凝收缩的凝聚力达到其抗张强度时，岩石(浆)内部发生潜在破裂和微形变；当潜在破裂面形成后，因岩石的泊松效应，微小潜在破裂面处的应力状态发生重整，形成新的潜在破裂面；当新的潜在破裂面处的剪应力等于岩石抗张强度时，岩石(浆)发生剪切破裂，形成如今所见的柱状节理。根据前人相关岩石实验数据，推算得到玄武岩相应温度下的内摩擦角、黏聚力、抗张强度和泊松比，采用应力莫尔圆方法进行数值计算，获得玄武岩在冷却到800 ℃左右时发生破裂，六棱柱形柱状节理开始形成，内角约119.1°。进一步分析认为，岩石的黏聚力、石英含量等因素可能控制着柱状节理的发育和形状。

早在17世纪，Foley 和 Molyneux(1694)、Molyneux(1698)就曾精确地描述了北爱尔兰巨人堤道柱状玄武岩接头的柱长、构造和多边形截面的形态特征；Phillips等(2013)统计了苏格兰staffa地区的玄武岩柱状节理多呈现六边形，内角约为120°；我国四川省大坝玄武岩柱状节理的产状亦显六边形，且节理面产状较为稳定，数据统计表明玄武岩柱状节理规律性明显，成因上具有一致性(Cui Jie et al.,2018)。Gerhard Müller (1998)用淀粉和水混合物的干燥过程模拟了柱状节理的形成过程；Hamada 等(2020)依据热传导理论将岩浆冷却过程中的热扩散与淀粉水混合物中水的扩散方程进行类比，较好地解释了玄武岩柱状节理多种结构的形成机制。关于玄武岩六边形柱状节理的成因主要有以下两种观点：

(1)方世明等(2011)和李全海等(2013)认为玄武岩的柱状节理是由于冷却引起岩石体积收缩，从而使得岩石破裂形成。

(2)隋建立等(2015)提出岩浆冷却过程中，岩层顶层处于较低温的大气或水中，而底层位于温度较高的散热慢，因而在顶层与底层间存在明显的温度梯度，此时岩浆在固/液边界线之下一个有限的厚度范围内发生贝纳德对流，形成六边形的对流“格子”。冷却过程中随着固/液边界线的向下移动，对流格子也不断向下移动，最终形成了柱状节理。

尽管如此，若柱状节理由岩石冷却发生张破裂而成，则破裂面为张性面，应表现为凹凸不平。野外观察到柱状节理的破裂面却较为平整，部分破裂面甚至出现擦痕(图1a)，这与第一种观点不符。另外，如果岩浆冷却过程中发生局部贝纳德对流，那么流动的液体会带动其中所含的衍晶质发生定向的移动，从而呈现贝纳德对流的流线，然而玄武岩柱状节理及其内部未发现斜长石斑晶定向排列(隐晶质玄武岩镜下可见斜长石晶体，因斜长石呈板条状，如果先结晶应随熔岩流定向，而实际观察并不定向，其他斑晶不具备这一特点)(图1b)，同样不符合第二种观点。鉴于此，在综合考虑张应力、剪应力、玄武岩的泊松比等因素的前提下，本文尝试对冷却过程中的玄武岩岩石微元进行严格的受力分析和数值计算，从定量的力学分析角度模拟推演玄武岩六边形柱状节理的形成过程，并对影响柱状节理形成及形态的因素进行初步探讨。

图1 (a)河北汉诺坝玄武岩柱状节理面上水平擦痕；(b)河北汉诺坝玄武岩显微照片(正交偏光)；山东昌乐玄武岩柱状节理实景图(c，d)；玄武岩柱状节理简化示意图(e)Fig.1 (a)Horizontal scratches on columnar joints of basalt in Hannuoba,Hebei;(b)Microphotograph of basalt in Hannuoba,Hebei (Cross polarized light);Field picture of basalt columnar joints in Changle area (c,d);Shandong Province;Simplified diagram of basalt columnar joints(e)

1 理论计算

基性岩浆喷发形成的玄武岩在冷却成岩过程中多会发生破裂，破裂后的玄武岩往往呈六棱柱状(图1c)，少数为五棱柱、四棱柱和三棱柱，柱状节理的延伸也并不一定平直(图1d)。本文以规范的六棱柱(图1e)为主要研究对象，探讨玄武岩柱状节理的形成机制。

1.1 模型建立

研究中取玄武岩的一微元，假设玄武岩在冷却破裂前为各向同性，则其所受各方向的应力基本相同。但由于岩石在局部存在微小差别，使得微元在两方向所受的力σ1,σ2有微小差别(不妨设σ1>σ2,σ1≈σ2，张应力为正)，从而发生微小形变(图2)。当玄武岩所受的张应力σ1与其抗张强度近似相等时，玄武岩将要在此微元处发生破裂。

图2 微元受力形变示意图Fig.2 Schematic diagram of micro-element force deformation实线为形变前，虚线为形变后The solid line is pre-deformation,whereas the dashed line is post-deformation

由于玄武岩泊松比的影响，微元发生形变后，其所受的张应力σ2的大小以及岩石的破裂方向将发生改变，设改变后的张应力为σ2′，与泊松比的取值有关。玄武岩的泊松比为0.23～0.32(张春生等，2019)，受温度影响，温度升高，岩石韧性增强，泊松比较小；温度降低，岩石脆性增强，泊松比较大,本文取平均值ν=0.28，则变化后的张应力为:

(1)

请注意，此时沿x方向的张应力σ2′将大于沿y方向的张应力σ1。重新分布后的张应力对微元的作用力如图3所示。图中σθ,σα代表张应力，τθ,τα代表剪应力，分别为σ1与σ2′沿法向和切向的分量，θ代表玄武岩破裂面与σ1方向的夹角。

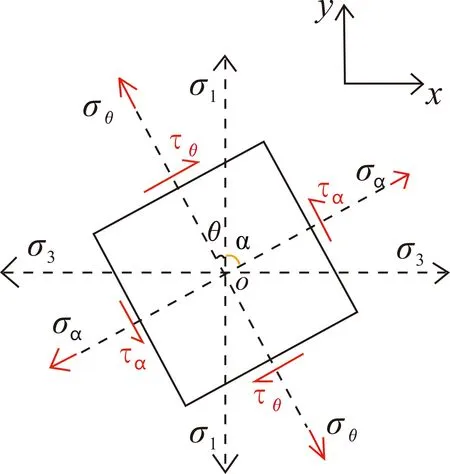
图3 微元所受应力的分析图Fig.3 Analytical diagram of the stress on the micro-element

σθ,σα,τθ,τα满足以下关系式 (Zheng Yadong et al.,2004):

(2)

(3)

在这些作用力下，岩石将沿τθ的方向发生剪切破裂，破裂的条件为:

τθ=τf

(4)

其中τf为岩石在相应温度下的抗剪强度。抗剪强度满足(孔祥国,2005):

τf=σθtanθc+c

(5)

其中，θc为岩石的内摩擦角，c为岩石的黏聚力，均与岩石本身的性质及温度有关。

1.2 岩石力学性质

1.2.1 玄武岩的抗张强度

玄武岩的抗张强度σmax约为18.5 MPa (张春生等，2019)，根据前面的分析，成立:

σ1≈σmax=18.5 MPa

(6)

1.2.2 玄武岩的抗剪强度

因未能直接获得玄武岩在高温下的相关实验数据，本文借鉴长石砂岩的数据进行估计。图4(a)为长石砂岩黏聚力随温度变化的实验曲线；图4(b)为长石砂岩内摩擦角随温度变化的实验曲线。选择长石砂岩的主要原因在于，长石砂岩中的石英含量较小，而玄武岩中基本不含石英，两者的相似性较高(石英会在600 ℃左右熔融，因而对岩石的黏聚力及内摩擦角的大小影响较大)(明杏芬和明晓东，2017)。长石砂岩的内摩擦角θc与温度近似满足:

图4 (a)长石砂岩黏聚力随温度变化的实验曲线；(b)长石砂岩内摩擦角随温度变化的实验曲线(据明杏芬和明晓东，2017)Fig.4 (a)Experimental curve of cohesion of feldspar sandstone with temperature;(b)Experimental curve of internal friction angle of feldspar sandstone with temperature (modified after Ming Xingfen and Ming Xiaodong,2017&)

θc=30.27-0.03t+5.35×10-5t2-

3.28×10-8t3

长石砂岩的黏聚力c与温度近似满足:

c=46.53-0.09t+1.28×10-4t2-

8.02×10-8t3

其中t表示温度，单位是摄氏度(℃)；θc的单位为度(°)；c的单位为MPa。

为了获得玄武岩相关参数，考虑到玄武岩与石英砂岩在200 ℃时都处于脆性，性质较为相似；在1000 ℃时都为熔融状态，性质较为相似。由于玄武岩中几乎不含石英，为消除石英所带来的影响，本文取长石砂岩在200 ℃与1000 ℃间的连线作为玄武岩内摩擦角、黏聚力与温度的关系曲线，对玄武岩的性质进行估计，得到玄武岩内摩擦角、黏聚力与温度间的线性关系。

玄武岩的内摩擦角θc与温度近似满足:

θc=-6.48×10-3t+27.45

(7)

玄武岩的黏聚力c与温度近似满足:

c=-3.59×10-2t+40.19

(8)

1.3 数值计算

将(2)代入(5)，并依据(3)、(4)得到:

tan(θc)+2c

由公式(2)、(3)、(4)、(5)，可得到θ满足如下关系式:

(9)

依据玄武岩的力学性质(6)、(7)、(8)进行数值计算，计算结果见表1，当玄武岩浆冷却至800 ℃时，柱状节理开始形成，呈六棱柱形，内角约119.1°。

表1 不同破裂温度下的破裂角大小Table 1 The size of the rupture angle at different rupture temperatures

2 影响柱状节理发育及形状的因素探讨

2.1 影响柱状节理发育的因素

自然界中柱状节理主要发育于玄武岩，少量可见于安山岩和流纹岩中。柱状节理不发育于安山岩和流纹岩的影响因素可能有2类：① 岩石的黏聚力。例如流纹岩黏聚力较大，一则可能使得岩浆从火山孔喷出后便呈现块状，无法形成熔岩流；二则使得流纹岩抗张强度较大，在实际的冷却过程中张应力及剪应力难以超过流纹岩的抗剪强度。② 岩石的石英含量。石英在600 ℃时发生相变，使岩石的体积突然增大，流动性突然增强，从而改变了岩石的冷却过程。

2.2 影响柱状节理形状的因素

自然界中除六棱柱外，也可见三棱柱、四棱柱、五棱柱以及七棱柱，但其分布比例不同。图5为四川、云南交界处二叠系峨眉山玄武岩柱状节理形状的统计图。

图5 四川、云南交界处二叠系峨眉山玄武岩柱状节理形状统计图(据Jiang Quan et al.,2014)Fig.5 Statistical map of columnar joint shape at the junction of Sichuan and Yunnan areas (modified after Jiang Quan et al.,2014)

不同地区的岩浆成分存在不同，岩石的黏聚力受其石英含量的影响。岩石的黏聚力增大，使得破裂方向与σ1的夹角变小，岩石倾向于形成五棱柱、四棱柱或是三棱柱，反之，则倾向于形成七棱柱。我们将(9)式等号左端记作y1，右端记作y2。随着黏聚力c的增大，y1随之增大，对应破裂角θ增大(图6)。相应地，破裂形成的多边形内角变小，倾向于形成边数更少的棱柱。考虑到七棱柱的内角约为128°，五棱柱地内角为72°，不妨假设，当破裂角θ在28°～42°之间时，柱状节理形成六棱柱。此时，在其他参量不变地情况下，黏聚力的范围为11.21～12.48 MPa。同时考虑到岩浆喷出的温度，环境造成的冷却速度的不同(明杏芬和明晓东，2017),也会对岩石破裂时的角度θ产生影响，造成柱状节理呈现不同的形状。这些分析将在后续的相关实验研究结果进一步定量证实。

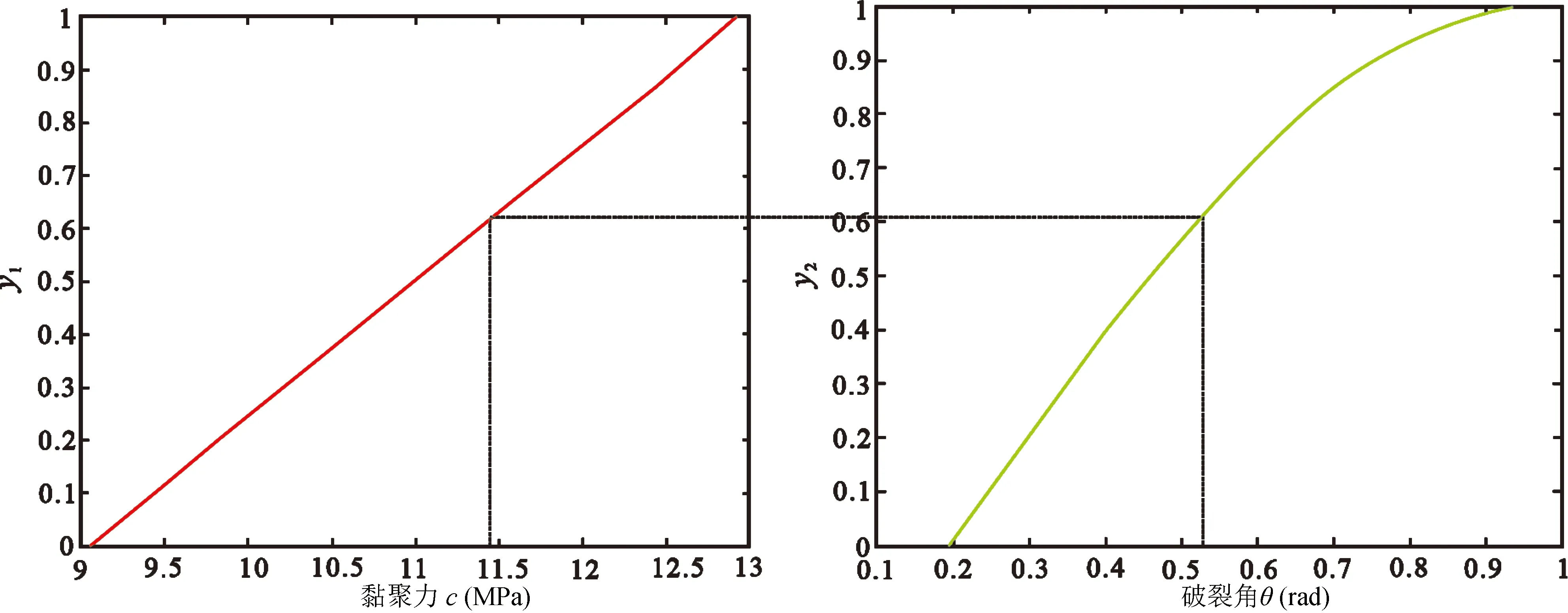
图6 破裂角θ随黏聚力c变化趋势Fig.6 Trend of fracture Angle θ with cohesion c

3 结论

(1)通过对玄武岩在冷却过程中受力情况的分析，提出岩石发生剪切破裂形成柱状节理的理论模型。即：当岩石(浆)冷凝收缩的凝聚力达到其抗张强度时，岩石(浆)内部发生潜在破裂与微形变；当潜在破裂面形成后，因岩石的泊松效应，微小潜在破裂面处的应力状态发生重整，形成新的潜在破裂面；当新的潜在破裂面处的剪应力等于岩石抗张强度时，岩石(浆)发生剪切破裂，最终柱状节理形成。

(2)根据玄武岩相应温度下的内摩擦角、黏聚力、抗张强度和泊松比进行数值计算，当玄武岩浆冷却至800 ℃时，柱状节理开始形成，呈六棱柱形，内角约119.1°。岩石的黏聚力、石英含量等因素影响着节理的形成和发育形态。本文从定量的力学分析角度为玄武岩六边形柱状节理的形成提供了全新的解释。