地下水人工补给过程中流速对多孔介质胶体堵塞的影响机理

冶雪艳，李铮，罗冉，宋亚霖，崔瑞娟

（1 吉林大学新能源与环境学院，吉林长春130021； 2 吉林大学地下水资源与环境教育部重点实验室，吉林长春130021）

引 言

地下水人工补给通过增加地下水资源的储存量以及提高和稳定地下水位，成为解决地下水过量开采及其环境问题（如海水入侵、地面沉降、湿地萎缩等）的重要措施。但受回灌过程中介质堵塞问题的阻碍，地下水人工补给在工程实践中的运用并不普遍。堵塞是由于物理、生物和化学过程而导致入渗介质渗透率下降的过程[1]。多孔介质堵塞涉及的过程多种多样且复杂，其机理分为物理堵塞、生物堵塞和化学堵塞[2-5]。根据以往研究，物理堵塞已被确定为最常见的堵塞形式[6-7]。物理堵塞主要是由于水源中无机和有机悬浮物引起的[8]，在补给过程中，悬浮固体颗粒滞留在含水介质中发生物理堵塞[9-10]。一些学者进行了定量研究，指出粒径与多孔介质直径之比对饱和多孔介质中的颗粒堵塞起着重要作用[11-12]。Du等研究了悬浮物堵塞的机理和影响因素，根据有效介质孔径（Dp）与悬浮物中位粒径（d50）的比值，将悬浮物堵塞分为表面堵塞、内部堵塞和混合堵塞, 并说明即使在高流速下，砂柱中也会沉积部分悬浮物，并且很快出现多孔介质的堵塞[13-14]；并进一步通过室内实验，证实了人工补给水源中的胶体在饱和多孔介质的堵塞过程中起着重要作用，即使少量胶体也可能导致多孔介质的渗透性大幅降低[15]。微小粒径的胶体在自然界中也广泛存在，这部分胶体引起的堵塞效应不容忽视。近年来，学者们对地下水人工补给过程中大颗粒悬浮物造成的堵塞问题研究较多[16-17]，对中间颗粒和胶体形成堵塞的微观机理研究尚不够充分[18]，这也说明人们对胶体等较小颗粒物的堵塞效应不够重视。虽然学者们已对影响胶体运动的因素进行了大量研究[19-20]，但针对地下水人工补给过程中多孔介质的胶体堵塞问题研究文献目前尚很少。

虽然人工补给过程中胶体类物质引起的堵塞从本质上看是一物理过程，但是近来越来越多的实验研究发现胶体阻塞不仅决定于物理因素，而且受溶液化学条件影响。Bradford等[21]指出，当胶体被阻塞在孔隙中后，施加在胶体上的各种作用力达到平衡，但是当溶液化学条件改变后，作用力的平衡将受到破坏，这些作用力包括重力、浮力、流体拽力、双电层力和范德华力等。Shen 等[22]的研究表明，增强溶液的离子强度可诱导胶体阻塞的发生。因此，在研究不同流速条件下的胶体堵塞特征时，补给水源的化学特征必须考虑，而且还要考虑实际人工补给系统的复杂性。例如，在地下水土环境中，含水层入渗介质通常是由不同大小、形状和粗糙性不同的岩土颗粒构成，这些复杂的因素均会综合产生影响。目前在人工补给过程中单一因素对堵塞的影响方面取得了一些研究进展，但是实际人工补给系统的复杂性及其补给过程中的堵塞机理，还有待结合入渗介质特征、水动力条件、水源特征做进一步的挖掘研究。

综上所述，由于入渗速率是地下水人工补给的关键指标，本文针对补给过程中多孔介质胶体堵塞的水流速度效应开展实验研究，分析流速变化时胶体在多孔介质中的迁移和滞留规律及原因，并同时考虑离子强度、介质粗糙度对胶体在多孔介质中迁移、滞留的影响。

1 实验材料和方法

1.1 实验装置和材料

本实验装置由供水装置、渗流装置柱、测压装置、取样装置和辅助装置五部分组成（图1）。

图1 实验装置示意图Fig.1 Schematic diagram of experimental setup

回灌系统中供水装置由玻璃烧杯、磁力搅拌器（JK-MSH-2L，上海精学科学仪器有限公司，中国）和蠕动泵（BT100-1F，兰格恒流泵有限公司，中国）组成；渗流装置柱子采用定制的有机玻璃柱，高16 cm，内半径1 cm，外半径2 cm；测压装置由压力传感器（A-10，WIKA 公司，德国）、数据采集器（CR1000，Campbell Scientific，美国）和计算机三部分组成；取样装置采用可定时定量自动采样的程控全自动部分收集器（CBS-A，上海沪西分析仪器厂有限公司，中国）。辅助装置有数控超声波清洗器（KQ2200 DB，昆山市超声仪器有限公司，中国）、旋涡混合器（QL-866，北京同德创业科技有限公司，中国）、烘干箱等。

渗透介质为河砂，其中位粒径（D50）为254 μm，曲率系数（Cc）为1.3，不均匀系数（Cu）为2.8（图2、表1）。河砂清洗去除悬浮杂质，用37%的盐酸浸泡24 h 去除介质表面可能存在的金属物质，用超纯水进行多次冲洗，测量上清液的pH 为6（与超纯水pH 一致），最后烘干并高温灭菌。

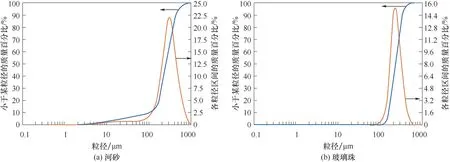
图2 河砂和玻璃珠粒度分析结果Fig.2 Particle size analysis of river sand and glass beads

表1 入渗介质粒径分布特征值Table 1 Characteristic value of particle size distribution of infiltration medium

为探究粗糙度对流速在影响胶体在饱和介质中迁移-沉积中的干扰作用，实验中的对照组采用玻璃珠（中位粒径250 μm）作为入渗介质，其处理过程与河砂相一致。经原子力显微镜（图3）测量其表面粗糙度，河砂和玻璃珠表面粗糙度（Ra）分别为52.0 nm、14.3 nm。

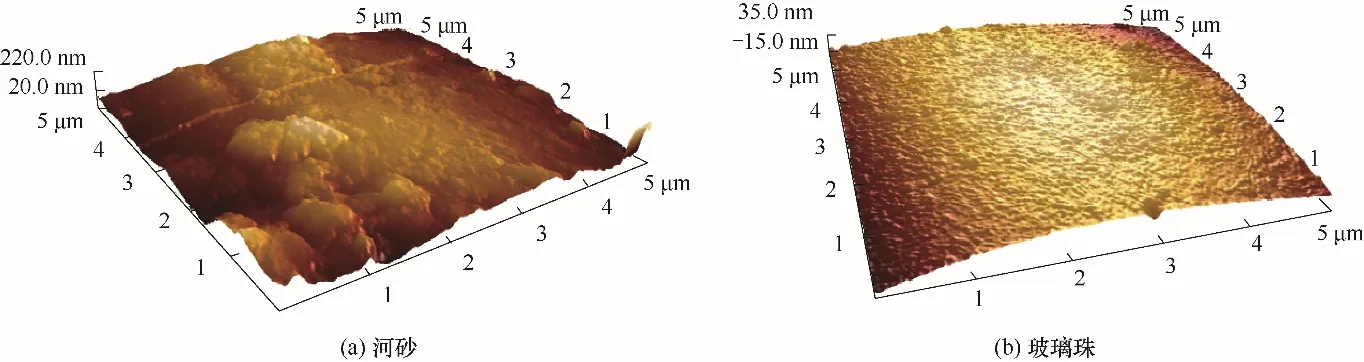
图3 河砂和玻璃珠原子力显微镜图Fig.3 Atomic force microscope images of river sand and glass beads

本次实验所用胶体为绿色fluoro-max 荧光微粒(Duke，美国)，这种微粒用聚苯乙烯合成，直径为2 μm。

1.2 实验方法

室内模拟实验砂柱采用湿法装填，将处理后的洁净河砂按1cm 间隔逐渐饱水填充至砂柱中，轻微搅动使空气排出、河砂饱水压实，孔隙度可由式(1)测出：

式中，ε为孔隙度；V水表示湿法装填消耗水的体积，cm3；V柱表示砂柱容积，cm3。

由式（1）计算得介质孔隙度均为0.43。考虑不同流速、不同离子强度、介质粗糙度（因玻璃珠与河砂都经过酸洗、纯水反复淋滤等处理过程洗掉介质表面的化学杂质[23]，且其主成分均为SiO2，忽略其表面化学特性影响）因素，设计5 组实验对照组（表2）。

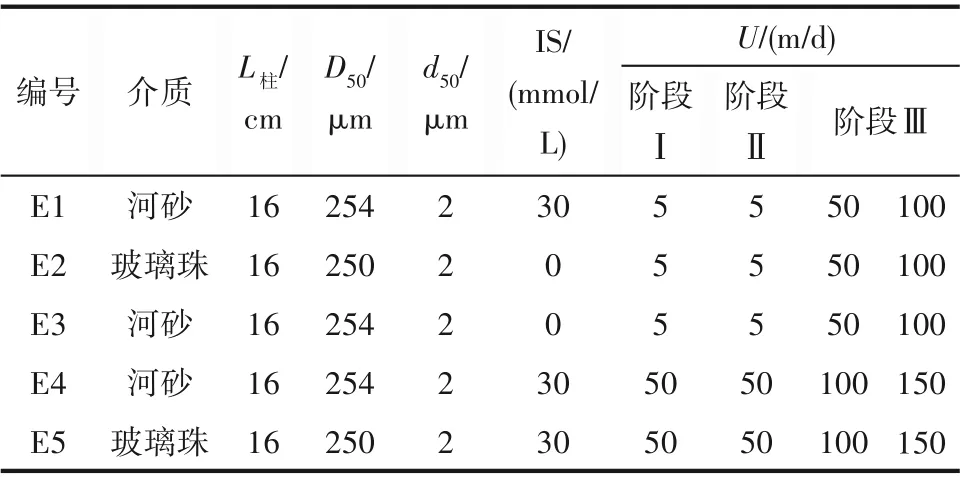
表2 实验方案Table 2 List of experimental schemes

实验按照如下3 个阶段开展。回灌阶段Ⅰ：注入具有已知初始浓度（C0）和确定离子强度（IS）的胶体悬浮液10 个孔隙体积（PV）；回灌阶段Ⅱ：注入与阶段Ⅰ离子强度相同的不含胶体的背景溶液3个孔隙体积；砂柱冲洗阶段Ⅲ：注入的冲洗溶液是与阶段Ⅱ离子强度相同且不含胶体的背景溶液，但流速要逐步增加，每个流速冲洗砂柱时间为3PV。实验过程中，按一定时间间隔（0.6～12 min）取样并采用紫外可见分光光度计在486 nm处测样品的吸光度值。

实验结束后完成砂柱拆解实验：进水端1 cm 范围内的砂柱按0.5 cm 厚度分层采集全部介质，其余15 cm 按1 cm 厚度进行介质采集，将采集的各层河砂分别放入15 ml 离心管中，用移液枪吸取8 ml 与每组实验阶段Ⅰ中离子强度相同的电解质溶液放入离心管，将离心管在QL-866 旋涡混合器振荡1 min 后静置1 h，空白样为同质量且相同处理的洁净河砂，用5 ml 注射器吸取上清液3.5 ml，测量回收的上清液吸光度值。

1.3 渗透系数计算

实验中采用压力传感器记录砂柱进水口、出水口部位水头，利用达西定律[式（2）]计算出各时刻传感器之间砂柱的整体渗透系数，为表征胶体迁移过程中含水介质渗透性的动态变化，求出各时刻砂柱整体相对渗透系数K/K0，其中K0为含水介质初始渗透系数(cm/s)，K为任意时刻的渗透系数(cm/s)。

则K计算公式如下：

式中，Q为渗透流量，cm3/s；L为渗透途径长度，即砂柱长度，cm；A为过水断面(在实验中相当于砂柱的横断面)面积，cm2；ΔH为砂柱进出水端水头值之差，cm；I为柱子整体的水力坡度。

1.4 水动力力矩计算

为了表征水流流速对胶体迁移-沉积的影响，采用水动力力矩计算公式[24-25]：

式中，Thyd为水动力拖拽力矩，N·m；ac为收集器半径，m；FH为拽力[26-27]，N；μ为流体的绝对黏滞度，Pa·s；vθ为流体的切向流速，m/s；r为径向坐标，m；ap为胶体半径，m。采用Happel 模型来描述多孔介质的流场，其中vθ可表示为

式（5）中的∂vθ/∂r可表示为：

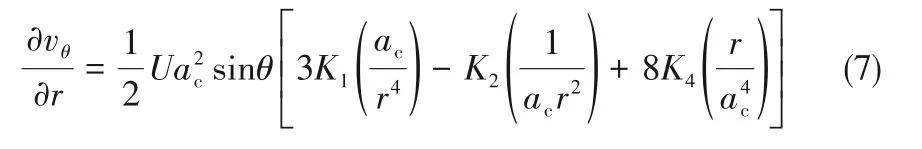
式中，U为达西流速，m/s；采用球坐标系参数：θ为切向坐标，rad；Ki为流函数中依赖于孔隙度的参数：

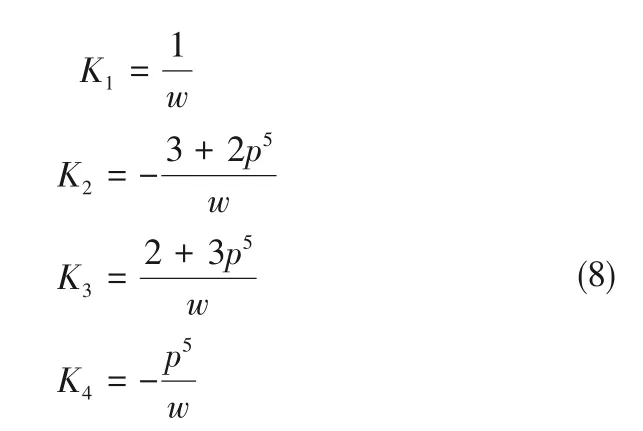
其中，w和p分别定义为

1.5 胶体迁移沉积数值模拟

1.5.1 多孔介质中胶体输送方程 根据质量守恒定律，在一维条件下，x方向上无穷小单元的胶体粒子流入量减流出量等于单位时间内胶体数量的变化量，可表示为[28]:

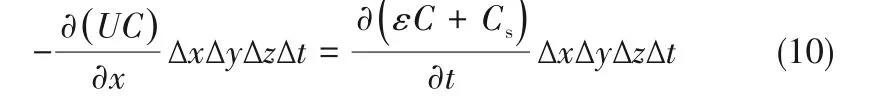
式中，C为水中悬浮物浓度，kg/m3；Cs为单位体积内沉积于孔隙内的悬浮物质量，kg/m3。

因此，运移方程可以导出如下：

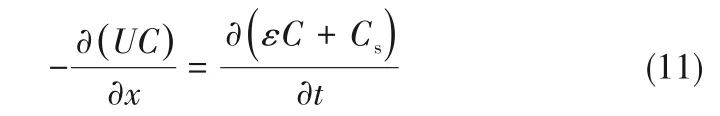
其中，孔隙度ε随胶体的吸附量变化，可表示为：

式中，σ为单位质量胶体堵塞孔隙体积，根据所购胶体颗粒密度算得，取值1.1×10-3m3/kg。

胶体运移和沉积方程涉及吸附和解吸过程，根据DLVO 理论，胶体颗粒和多孔介质之间相互作用可用范德华力、双电层力、水合力和空间排斥力表示，胶体的表面沉积是一个水动力过程[29]，为了简化计算，假设胶体的吸附和解吸是同时发生的，沉积方程可以表示为[30]：

式中，α为胶体吸附系数，s-1；β为胶体解吸系数，s-1。

1.5.2 模型的应用 首先建立概念模型，以概化多孔介质的内部结构、边界性质、水动力条件，在COMSOL Multiphysics 5.5 平台建立一维模型对5 组实验进行数值模拟，每1 cm 划分一个节点，共划分为16 个域和17 个节点（图4），在全局定义中输入基本参数（ε0、α、β、σ），组件1中定义变量（ε、C0、U），插入2个系数形式偏微分方程分别构建胶体的运移方程和沉积方程，在运移方程下设置狄利克雷边界条件C0，构建网格并分别设置模拟时间步长，运行模型，并以R2为判别标准，将穿透曲线及沉积曲线与实测值进行对比。因本次拟合参数较少，根据实验穿透数据，反复调整α、β数值（0＜α＜1、0＜β＜1），进行穿透曲线的拟合。

图4 用于数值建模的概念模型Fig.4 The conceptual model used for numerical modeling

综上，数学模型构建为：

1.5.3 数学模型的验证 应用数学模型拟合E1～E5的穿透曲线及末时刻拆柱的沉积曲线（图5、图6），得到胶体吸附和解吸系数（表3），系数范围与前人所得范围一致[31]。可以看出流速影响了胶体在多孔介质中的滞留-迁移[32]，但离子强度较大影响了堵塞的流速效应。这种影响可以从胶体吸附系数体现：对比同介质实验组（E1 和E4），流速为50 m/d 时的胶体吸附系数达到5.9×10-3s-1，而在5 m/d 时的吸附系数较小为1.6×10-3s-1，表现为流速越大，胶体吸附系数越大[33]，原因是高流速下单位时间可输送较多胶体；对比离子强度对吸附系数的影响（0 mmol/L和30 mmol/L），高离子强度胶体吸附系数远大于（2 个数量级）低离子强度，说明离子强度对胶体沉积产生了影响[34]。

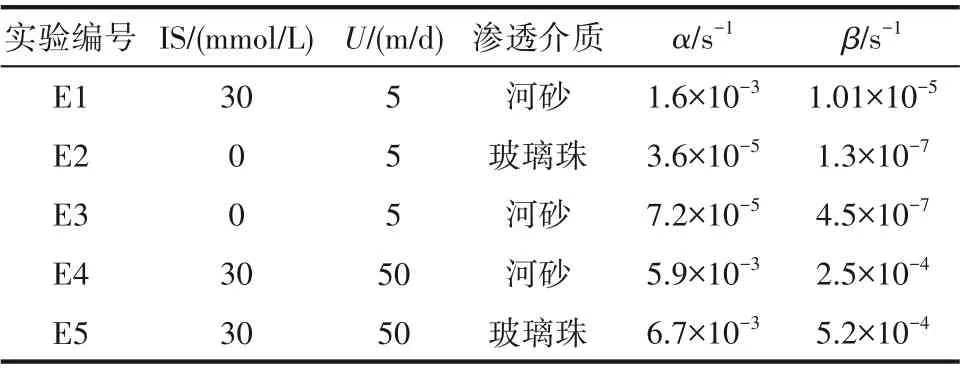
表3 COMSOL模拟不同条件下胶体吸附解吸参数Table 3 COMSOL simulation of colloid adsorption and desorption parameters under different conditions

图5 穿透曲线模拟结果Fig.5 Penetration curve simulation results

图6 沉积曲线模拟结果Fig.6 Deposition curve simulation results

2 结果与讨论

2.1 胶体在多孔介质中的迁移特征

对比不同流速条件（E1、E4实验）下胶体在河砂介质中的穿透曲线（图7）可以看出：孔隙水流速对胶体在饱和多孔介质中的滞留-迁移有很大影响。在相同的介质和离子强度条件下，流速为5 m/d（E1）时，穿透曲线峰值低于0.04，胶体在砂柱中运移过程中几乎全部沉积在了含水介质中；当流速增加到50 m/d（E4）时，穿透曲线显示穿透值增大了一个数量级，近似达到0.4。随着流速的增加，胶体迁移量增多，胶体穿透曲线的峰值升高，并且流出液中胶体浓度也升高，这与姚舜译等[35]的研究相符。这表明孔隙水流速越高，越有利于胶体在饱和含水介质中的迁移，而不利于胶体的沉积。主要原因是由于孔隙水流速增大会减少胶体和砂颗粒的接触时间，使得胶体吸附的可能性大大降低，这与殷宪强等[36]的研究结论一致；另外，孔隙水流速增加，会在介质孔隙中产生更大的水力拖拽力，使得胶体具有更大的推力随水流迁移，有利于胶体的迁移；此外，胶体在多孔介质中运移会发生沥滤（单颗粒粒径太大而堵在细小孔隙喉道）过程[37-38]，流速下降则会使沥滤作用增强，使更多的胶体滞留在多孔介质中。胶体颗粒无法通过较小孔隙体积而被滞留在多孔介质中，比如滞留在介质表面粗糙的位点上、颗粒与颗粒的接触位点上或通过水力桥接（当足量胶体同时到达孔隙收缩处，并且被流体动力推向孔隙入口，形成桥接）和大小排斥滞留沉积在多孔介质内部，流速较大时，由于较大的水动力条件可突破部分不稳定桥接堵塞，增加突破曲线穿透值。

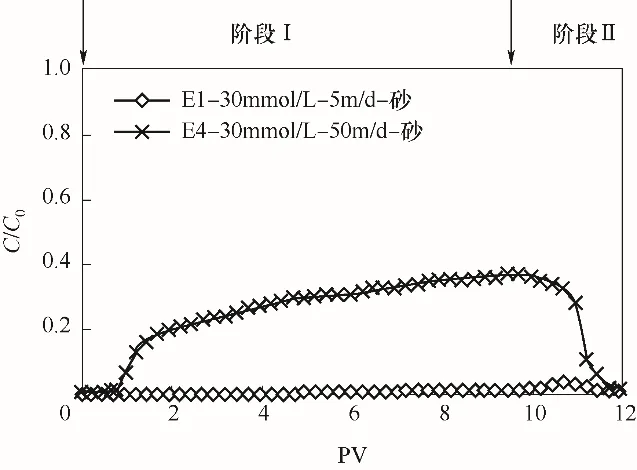
图7 不同流速的穿透曲线Fig.7 Penetration curves with different flow rates

对比不同离子强度影响下（E1 和E3）胶体在多孔介质中的穿透曲线（图8）：当孔隙水流速为5 m/d（E3）时，去离子水条件下的胶体穿透效果好，在阶段I 初期，胶体相对浓度迅速上升，之后达到相对稳定（C/C0基本稳定在0.82），阶段Ⅱ时流出液中胶体的浓度又因背景溶液不含胶体而减小，峰值为0.82，这表明相当大一部分胶体随水流迁移出流，少部分胶体在砂柱中运移时沉积在了含水介质中。而在离子强度为30 mmol/L（E1）条件下，胶体以沉积作用为主，这一现象与Sasidharan等[39]的结论相符。主要原因是由于补给水源离子强度增加，使胶体和砂颗粒表面重叠的扩散双电子层厚度被压缩，使斥力势能减弱[40]，吸力势能不产生变化，能量势垒的高度减小且位置也发生了变化，次级势阱变深，相互作用力以吸引力为主，不利于胶体的迁移[41]；同时溶液离子强度增加也使胶体颗粒间的排斥力降低，有利于胶体絮凝，形成大颗粒，从而无法通过较小孔隙，迁移能力下降。图6 对比结果显示：在一给定的流速条件下，胶体的沉积量随着离子强度的增加而增加。在高离子强度条件下（30 mmol/L），胶体和介质之间的作用力强，胶体不容易受水动力条件影响随水迁移；反之低离子强度条件下（0 mmol/L），胶体和介质之间的作用力弱，易受水动力条件影响随水迁移。

图8 不同离子强度的穿透曲线Fig.8 Penetration curves of different ionic strengths

对比不同介质粗糙度条件下(E2 和E3、E4 和E5）胶体在多孔介质中的穿透曲线（图9）可以看出：无论是在高离子强度高流速的条件下，还是低离子强度低流速的条件下，胶体在玻璃珠介质中的穿透曲线峰值要高于河砂，即多孔介质的粗糙度越小，随水流流出的胶体越多，越有利于胶体在多孔介质中的迁移。这是由于粗糙的多孔介质表面凹凸不平，可以削弱水流的作用[42]。同时，由于多孔介质的粗糙度越大，意味着多孔介质对胶体所能提供的吸附、沉积位点会越多，利于胶体沉积。

2.2 胶体在砂柱中的沉积分布特征

随着水流流速增大，多孔介质胶体总的沉积量会减少。胶体沉积量从进水端至出水端呈现下降趋势（图10）；此外，在进水端E1（离子强度30 mmol/L，流速由5 m/d 加大到50 m/d 再到100 m/d）的胶体沉积量远高于E4（离子强度30 mmol/L，流速由50 m/d 加大到100 m/d 再到150 m/d）的胶体沉积量，E1 的胶体空间沉积分布曲线呈现“超指数分布状态”[43]，并且随孔隙水流速增大，胶体空间沉积分布曲线的超指数分布趋势会削弱，胶体的空间分布状态会改变，胶体沉积分布得更加平均。胶体在多孔介质的流动过程中，孔隙水流速越大，水流所产生的水力拖拽力越大，对胶体的流体拽力越大，增强胶体在介质中的迁移性[44]，从而使得阻碍胶体沉积的低渗流区体积减小[45]，不利于胶体的沉积，减少胶体在介质中的滞留量。当水流速越小，越有利于胶体滞留在多孔介质表面时，这种表面过滤的现象越明显，进入砂柱内部的胶体量越少，胶体沉积的空间分布越不均匀，胶体空间沉积分布曲线呈现“超指数分布状态”越明显，所以孔隙水流速的不同，会引起胶体的空间分布状态发生变化。

不同离子强度下胶体空间沉积分布曲线见图11。在相同流速条件下，回灌水的离子强度越低胶体在多孔介质中的沉积量也会很少，胶体空间沉积分布曲线的超指数分布趋势会十分微弱，胶体的空间分布状态会十分平均。这是由于离子强度降低时，胶体和介质颗粒表面扩散双电子层的厚度将变大，使得斥力势能增强，不利于胶体稳定和胶体滞留，有利于胶体迁移，使得表面过滤被削弱，随水流流出的胶体量增多，胶体沉积的空间分布越均匀，胶体空间沉积分布曲线呈现“超指数分布状态”越弱，因此离子强度的变化，也会引起胶体的空间分布状态发生改变。

不同介质粗糙度条件下胶体空间沉积分布曲线见图12。E2（介质为玻璃珠，IS=0 mmol/L，流速由5 m/d加大到50 m/d再到100 m/d）、E3（介质为河砂，IS=0 mmol/L，流速由5 m/d 加大到50 m/d 再到100 m/d）的胶体空间沉积分布曲线形态差别不大，胶体的空间分布状态十分平均，但E3的胶体沉积总量要略高于E2，说明粗糙度不是影响胶体沉积空间分布状态发生变化的主要因素，但会影响胶体在多孔介质中沉积的总量。根据吸附系数拟合结果，E3胶体吸附系数稍大于E2，分别为7.2×10-5s-1和3.6×10-5s-1。由于流动过程中，胶体以阻塞或者吸附的形式在砂介质中滞留，当胶体在水动力拖拽力的作用下沿着介质表面迁移至粗糙突起旁时，粗糙突起可产生平行水流方向上的应力来平衡水动力拖拽力，使胶体沉积在介质表面上，因此粗糙度越大，胶体在多孔介质中吸附系数越大、滞留的总量越多。

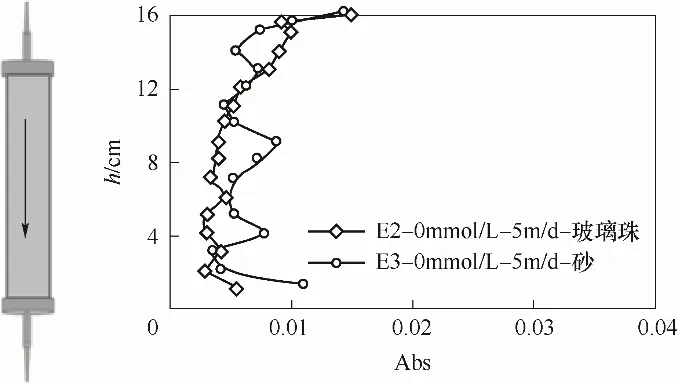
图12 不同介质粗糙度条件下胶体空间沉积分布曲线Fig.12 Distribution curves of colloidal space deposition under different medium roughness conditions

2.3 水动力力矩特征

胶体在特定位置的迁移和滞留取决于特定位置的力和力矩平衡[46]，选用了5、50、100、150 m/d 四种流速条件来研究水动力力矩的大小分布情况及流速变化对水动力力矩的影响。图13 为计算的水动力力矩分布情况，横坐标为水动力力矩，纵坐标Lmax代表胶体前、后驻点之间的距离，L代表点位到前驻点的距离。可以明显看出，4 种不同流速情况下，固相收集器表面附近胶体所受水动力力矩趋势一致，胶体均在固相收集器前、后驻点处所受水动力力矩最小，因此前、后驻点附近是胶体最容易形成吸附的区域[47]，胶体所受水动力力矩大小呈弧形曲线向中间递增，在中间位置所受水动力力矩最大，且随流速增大而增大。当流速增大，胶体所受水动力力矩曲线整体右移，前、后驻点附近点位胶体所受水动力力矩增大，当水动力力矩大于胶体所受黏附力矩时，部分可逆吸附的胶体解吸，随水流流出，验证了渗透系数的变化是由于水动力力矩的改变引起的胶体的迁移。

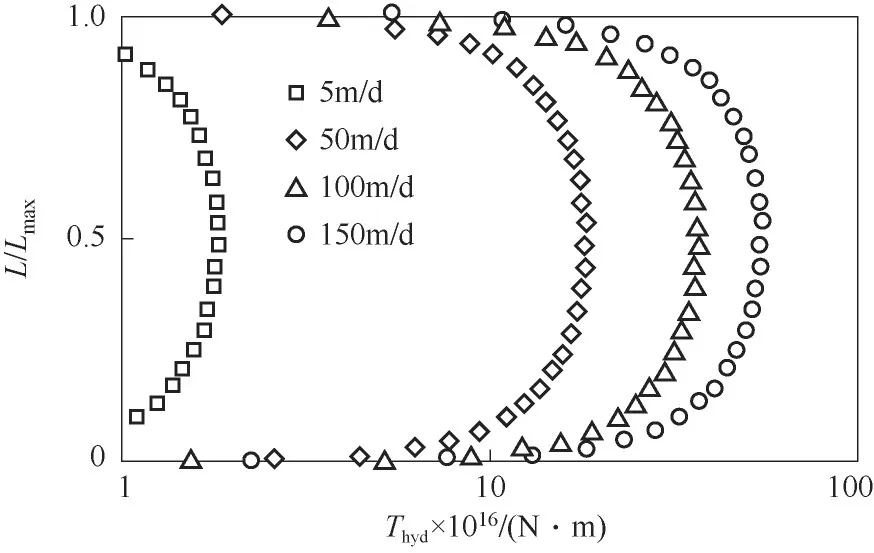
图13 不同流速条件下胶体在固相收集器表面所受水动力力矩Fig.13 Hydrodynamic moment of colloid on the surface of solid collector under different flow rates

2.4 多孔介质渗透性变化特征

图14显示了在不同的离子强度(IS=0 mmol/L 和30 mmol/L)和流速(U=5 m/d 和50 m/d)条件下的渗透系数变化。可以看出，渗透系数整体变化趋势都呈现先下降后基本平稳趋势。在初始阶段，渗透系数均有不同程度的降低，原因是胶体进入多孔介质造成介质堵塞，但在5 m/d水流流速条件下，E1中出现了较为急剧下降，这印证了低孔隙水流速高离子强度的条件下，多孔介质表面水力力矩小，胶体不易迁移，大部分沉积在多孔介质表面，迅速造成了堵塞，使多孔介质的渗透系数迅速下降；在实验Ⅱ阶段，水源中无胶体加入，渗透系数曲线保持平稳趋势。

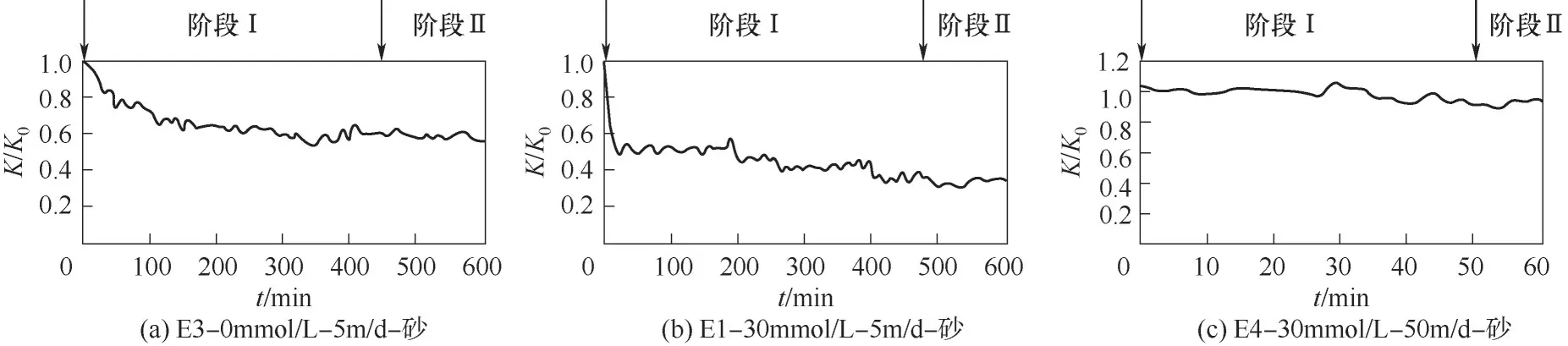
图14 回灌阶段Ⅰ、Ⅱ砂柱渗透系数变化曲线Fig.14 Variation curves of permeability coefficient of sand column in recharge stages Ⅰand Ⅱ

为探究流速突增对渗透系数的影响，观察当速度在恒定离子强度(IS=0 mmol/L 和30 mmol/L)且无胶体条件下增加到50、100或150 m/d 时渗透系数的变化趋势（图15）。3组实验的渗透系数变化趋势基本一致，在两次瞬间加速后，渗透系数均出现上升，这是由于作用在颗粒表面胶体上的扭矩和力平衡发生了变化：流速极大提高，产生了更大的水动力拖拽力，当胶体所受水动力拖拽力大于黏附力时，胶体解吸使得部分胶体可以从介质表面脱落释放，并随水流流出砂柱。此外，保留在一些孔隙收缩处的桥接在较高的水动力拖拽力下被移除[48]，导致砂柱内部孔隙空间增大,流速提升会导致胶体在砂柱内滞留量减少。在急剧上升之后出现下降趋势，原因是加大的水动力拖拽力使原本吸附在次级势阱的胶体解析下来，部分存在于浅的次级势阱中的胶体受水动力作用在固相收集器表面平移，到达新的有利于附着的位置形成新的吸附[49]，从图15可知水流流速的增大会恢复一部分胶体堵塞的孔隙渗透性。

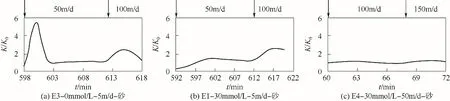
图15 冲柱阶段砂柱渗透系数变化曲线Fig.15 Variation curves of permeability coefficient of sand column during punching stage

2.5 水流流速对胶体堵塞的影响

观察冲柱阶段的穿透曲线（图16），将纵坐标放大可以明显看出5组实验胶体的释放大体一致且都有两次明显上升趋势，这两次急剧上升分别出现在13PV和16PV附近。这是因为在冲柱阶段流速急剧加大（E1、E2、E3 组流速由5 m/d 加速到50 m/d 再加速到100 m/d，E4、E5 组流速由50 m/d 加速到100 m/d 再加速到150 m/d），一方面水动力拖拽力相应加大，使得原本吸附在次级势阱的胶体，受到水动力拖拽力大于所受黏附力，因此一部分可逆吸附的胶体从固相收集器表面解吸下来随水流流出砂柱；另一方面胶体在介质表面特定位置的停留时间与速度成反比，胶体在收集器表面特定位置的停留时间缩短（例如，流速增加）降低了随机布朗运动获得足够动能而被势阱吸附的概率，降低胶体滞留的可能性，从而使胶体更容易迁移排出。对比图16（a）、（b），可以看出，无论是在低流速条件还是高流速条件下，每一次流速的增加都对应一次胶体的脉冲式释放，胶体的释放使砂柱内孔隙度增大，渗透系数上升，验证了渗透系数随着流速的增大而增大是由流速的增加形成更大的水动力拖拽力矩使胶体迁移而引起的。这也说明加大流速对胶体迁移有利，使已经形成堵塞的部分胶体释放，渗透系数有所恢复。

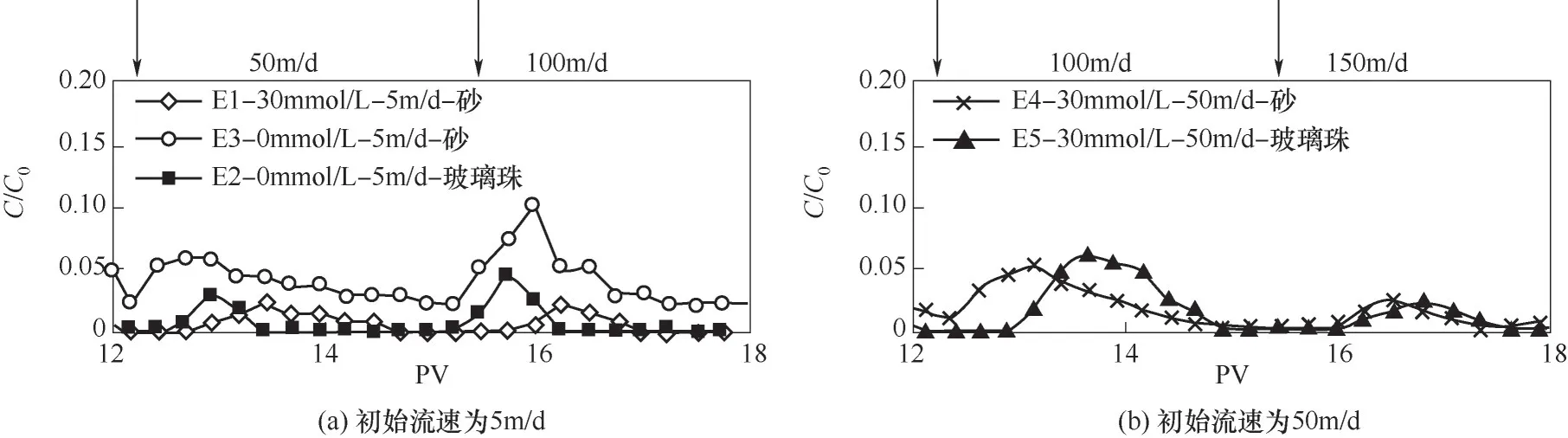
图16 不同实验条件下的冲柱阶段穿透曲线Fig.16 Penetration curves of punching stage under different experimental conditions

3 结 论

（1）通过室内砂柱渗流实验验证了水流流速对胶体颗粒在多孔介质中的迁移、滞留过程的影响。结果表明回灌水流速的增大会增加胶体在砂柱介质里的迁移量，降低胶体颗粒在介质中的滞留量；相反，回灌水流速的降低会造成胶体在多孔介质中的滞留，水动力力矩计算结果显示，回灌水流速越高，水流拖拽力越强，越不利于滞留。

（2）回灌过程中胶体在多孔介质中的沉积会造成渗透系数下降，但回灌流速的瞬间加大，会使已形成堵塞的部分胶体释放从而导致介质渗透性在短时间内有所恢复，然而随着新吸附的形成，渗透性仍会逐渐下降。水源离子强度和介质粗糙度会影响胶体迁移的流速效应：离子强度增加使胶体和介质表面相互吸引作用增强，有利于吸附；粗糙度的增加可削弱水动力拖拽力作用，同时增加吸附、沉积点位和接触面积，有利于胶体沉积。

符 号 说 明

A——过水断面(在实验中相当于砂柱的横断面)面积，cm2

ac——收集器半径，m

ap——胶体半径，m

C——水中悬浮物浓度，kg/m3

Cs——单位体积内沉积于孔隙内的悬浮物质量，kg/m3

C0——进水悬浮物初始浓度，kg/m3

D50——介质中位粒径，μm

d50——胶体中位粒径，μm

FH——拽力，N

ΔH——砂柱进出水端水头值之差，cm

I——柱子整体的水力坡度

K——砂柱整体的渗透系数，cm/s

Ki——流函数中依赖于孔隙度的参数

K0——含水介质初始渗透系数，cm/s

L——渗透途径长度，cm

L柱——砂柱长度，cm

Q——渗透流量，cm3/s

Ra——表面粗糙度，nm

r——径向坐标，m

Thyd——水动力拖拽力矩，N·m

U——达西流速，m/s

V水——湿法装填消耗水体积，cm3

V柱——砂柱容积，cm3

vθ——流体的切向流速，m/s

α——胶体吸附系数，s-1

β——胶体解吸系数，s-1

ε——多孔介质的孔隙度

θ——切向坐标，rad

μ——流体的绝对黏滞度，Pa·s

σ——单位质量胶体堵塞孔隙体积，m3/kg