基于有限元的典型换热结构比较研究
张泽昀,钟 飞,李 博,夏军勇
(湖北工业大学机械工程学院,武汉 430068)
换热器是一种广泛应用在化工、动力、食品,药业和轻工等工业领域的能源转换设备,在能源的有效利用上扮演了重要角色。换热器的结构会直接影响到能源利用率和能耗水平。因此,各国的学者们对换热器结构开展了大量的研究,并从中获得了许多重要的实验参数和模拟结果。在典型的换热结构中,肋片是最简单,也是应用最广泛的一种形式。对于肋片尺寸参数的研究包括形状、截面比、间距、倾斜角度和排列方式等[1-3]。平直排列的肋片表现出更好的传热效率,但是相邻2 排肋片之间的区域会造成流动阻力的增加;而倾斜排列的肋片具有更好的流动性能。换热器中的球凸结构已成为近年来比较热门的研究课题,球凸的直径、深度、间距和排布对其性能的影响的研究结果能为球凸几何结构的优化提供实验依据[4-6]。三角形结构作为另一种强化传热结构,也受到了不同研究机构的广泛关注。也有文献报道了对三角形结构中间距、倾角、高度等几何参数对传热阻力性能的影响[7-8]。
本研究围绕换热器结构对热学性能的影响进行,其主要内容是对整体尺寸相同,但是结构不同的9 种换热器(包括2 种肋片结构、3 种球凸结构、3 种三角结构和1 种混合结构的换热器)内部的温度分布和流体速度变化进行数值模拟,并从传热效率,流动阻力以及综合传热系数3方面进行比较和分析。
1 计算模型的建立
为了减少尺寸参数对性能的影响,换热器几何模型的整体尺寸保持不变,即长100 mm、宽15 mm、高12 mm,壁厚1 mm。边界条件在不同换热器的数值模拟过程中也保持同样设置:换热器内部流体为空气,入口边界选择velocity inlet,入口速度设置10 m/s,入口温度300 K,出口边界条件为outflow,壁面温度600 K。
激活能量方程,由于是本研究属于低雷诺数流动,根据文献[9]的对比结果,采用标准RNGκ-ε模型的模拟结果最接近实际测量结果,因此选择RNGκ-ε湍流模型进行数值计算。不同结构换热器的数值模拟均在ANSYS19.0 中ICEM 模块中进行建模和非结构性网格划分,并在FLUENT 模块中进行计算[10]。
2 结果与讨论
2.1 肋片结构的影响
2种肋片布置形式下换热器的结构如图1所示,2 种换热器内部肋片分别为同排布置和交错布置,肋片长度4 mm、厚度1 mm,相邻肋片间距9 mm。

图1 肋片换热器的2种结构Fig 1 Two structures of fin heat exchanger
图2为是2种肋片结构换热器的通道中截面和出口端面的温度分布云。
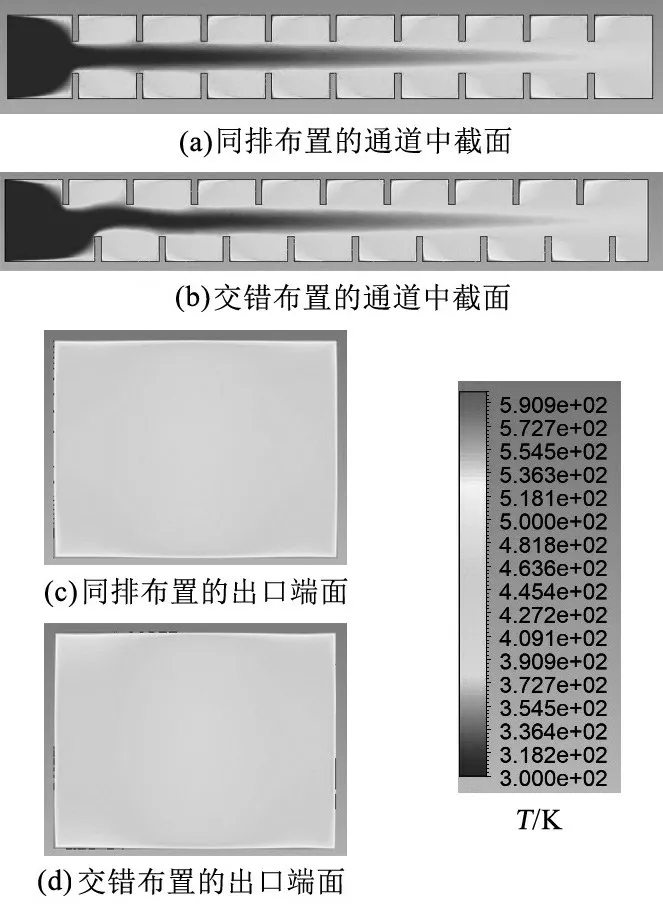
图2 2种肋片换热器的温度分布云Fig 2 Temperature distribution of two kinds of fin heat exchanger
由图2可知,300 K的空气从2种不同结构换热器的左侧入口进入,流经肋片结构的通道后,温度明显上升,2 种情况下空气在出口中心的温度均能达到约390 K。在中心轴上,空气温度随着远离入口方向距离的增加而均匀上升。在同一轴向距离上,离壁面越近,温度越高。模拟结果揭示了2种结构下,换热器的传热效率几乎一致。由此可见,肋片的位置排布对于温度场分布的影响较小。
图3为2种肋片结构换热器通道中截面的速度分布云。

图3 肋片换热器通道中截面速度分布云Fig 3 Velocity distribution in fin heat exchanger
由图3可知,入口速度10 m/s的空气,经过第1 排肋片的中间区域后,速度快速提升至36 m/s,达到入口平均速度的3.6 倍;之后速度缓慢下降,在出口前约3 mm 位置处下降至30 m/s,再经过一个快速下降的速度梯度,最终在出口处的速度为18 m/s。在2 种不同肋片排布下,相邻两排肋片之间均出现了较为明显的涡旋结构。而且离入口越近,涡旋越明显。
速度在第1排肋片处明显上升,其原因主要是因为开口突然减小,流体受到剪切应力,产生了较强的流动冲击,使湍流动能立即增大;而在之后的一段距离内,空气流动被限制在中心轴附近,因此速度变化较小;在通过最后一排肋片之后,空气进入开阔地带,剪切应力明显减小,出现明显的速度下降梯度。
综合上述模拟结果可以看出,在换热器中采用肋片结构,能够明显改变内部流体的传热和流动,产生明显的涡旋现象。但是肋片同排布置和交错布置,对于流动传热性能没有明显的影响。
2.2 球凸结构的影响
球凸结构与肋片结构相比,由于没有尖锐部分,过渡部分更加光滑,因此理论上具有更好的流动特性。对圆球形、横向椭圆形和纵向椭圆形的3 种结构进行分析。具体结构如图4 所示。图4(a)中球凸的半径2.5 mm,高度2.5 mm,相邻两球心之间的距离为10 mm;图4(b)中纵向椭圆形球凸的长轴半径5 mm,短轴半径2.5 mm,相邻两球心之间的距离为10 mm;图4(c)中横向椭圆形球凸的尺寸与纵向椭圆形球凸的尺寸完全一样,相邻两球心的距离为16 mm。
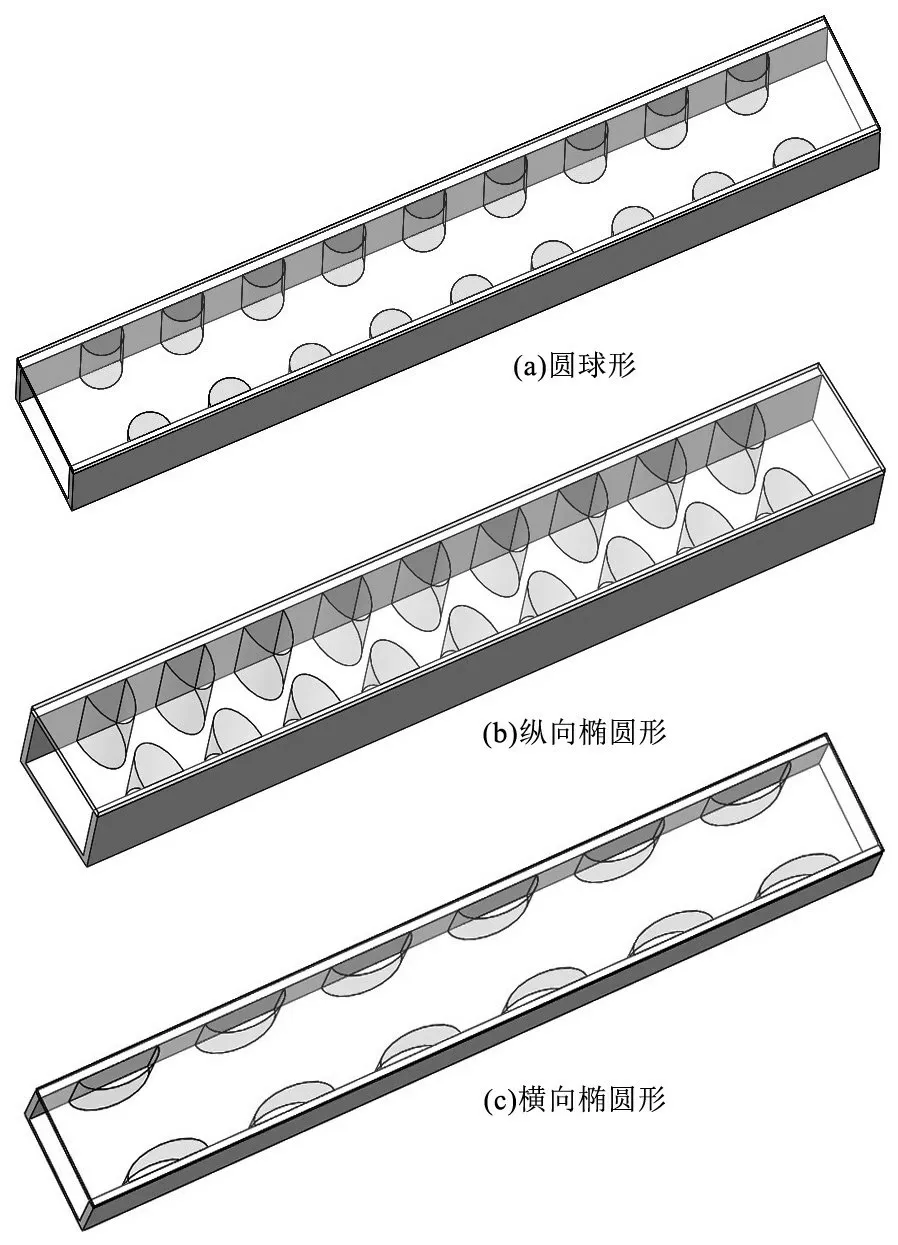
图4 球凸换热器的3种结构Fig 4 Three structures of spherical convex heat exchanger
图5 和图6 分别是3 种球凸结构换热器的通道中截面和端面温度分布云。

图5 3种球凸结构换热器通道中截面温度分布云Fig 5 Temperature distribution in the channel of three kinds of spherical convex heat exchangers

图6 3种球凸结构换热器通道出口端面温度分布云Fig 6 Temperature distribution at channel outlet of three kinds of spherical convex heat exchangers
由图5可知,纵向椭圆形球凸的出口中心空气温度最高,其次是横向椭圆形球凸,圆球形球凸的出口中心的空气温度最低。近壁面的温度从高到低的排列顺序是:纵向椭圆形球凸、圆球形球凸、横向椭圆形球凸。这说明不同结构的球凸对换热器传热性能的影响较大,纵向椭圆形球凸的布置方式下,同排2个球凸之间的间距最小,空气受到的冲击更大,同时空气与壁面的接触面积也最大,2者同时作用,造成这种结构的传热效率最高;而在横向椭圆形球凸的布置方式下,虽然同排2 个球凸之间的间距最大,对空气的冲击较小,但是空气和壁面的接触面积与圆球形球凸结构相比更大,强化换热效果优于圆球形球凸结构。
由图6可知,其中圆球形球凸的出口中心呈现处椭圆状的低温区域,中心温度大小约为353 K;纵向椭圆形球凸的出口端面温度分布较为均匀,约418 K,没有观察到特别明显的温度变化梯度;而横向椭圆形球凸的出口端面出现“∞”形状的低温区域,最低温度约366 K。对于圆球形球凸结构,中心流动的湍流一般出现在中心区域,而纵向椭圆形球凸中空气射流被压缩,低温区域变得不明显,但是在横向椭圆形球凸中,湍流开始向两侧横向扩散,形成2个较小但对称的涡旋中心。
图7为3种球凸结构中截面上的速度分布云。
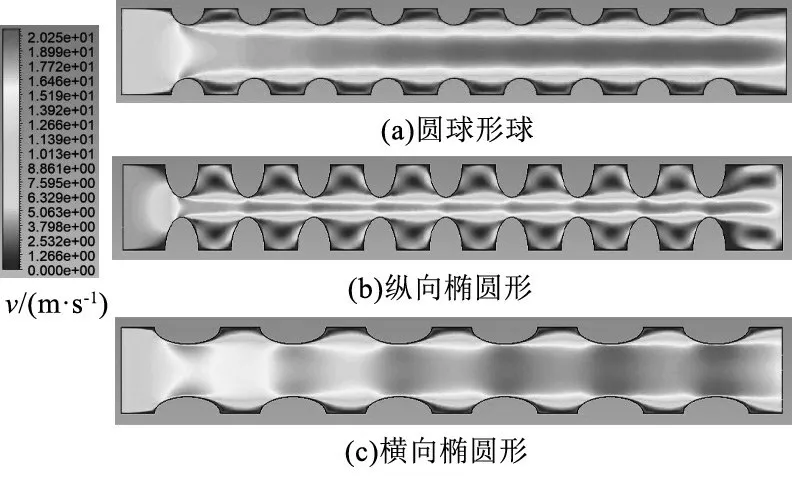
图7 3种球凸结构换热器通道中截面的速度分布云Fig 7 Velocity distribution in the channel of three kinds of spherical convex heat exchangers
由图7可知,横向椭圆形球凸结构的出口速度最小,为16 m/s;其次是圆球形球凸结构,为17 m/s,纵向椭圆形球凸的出口速度最大,为25 m/s。在纵向椭圆形球凸的近壁面附近,还可以观察到明显的涡旋结构。这主要是由于纵向椭圆形球凸结构下,相邻两球凸之间的空间区域较大,空气能够发生较强的流动分离然后再混合,其湍流程度会随着再次混合而增强,从而提高了湍流动能。
综合上述分析,不同球凸对换热器内部流体的传热和流动都有明显的影响。而纵向椭圆形球凸结构的传热和流动性能都明显优于其他2 种结构,可以作为球凸结构下实际应用中的首选方案。
2.3 三角结构的影响
三角结构换热器,以及变化而来的正弦波浪结构换热器,被广泛应用在化工领域。倾角15°、30°和45°的3种三角结构换热器结构如图7所示。三角形最长边8 mm,相邻两三角的中心距离13.5 mm。

图8 三角形换热器的3种结构Fig 8 three structures of triangle heat exchanger
图9和图10分别为3种三角凸结构换热器的通道中截面和出口端面温度分布云。

图9 三角凸结构换热器通道中截面温度分布云Fig 9 Temperature distribution in the channel of triangular convex heat exchanger

图10 三角凸结构换热器出口端面温度分布云Fig 10 Temperature distribution at channel outlet of triangular convex heat exchanger
由图9 和图10 可知,15°倾角三角凸结构的出口中心的空气温度最低,仅为347 K,低温空气射流从入口几乎扩展到出口,而在出口端面的云图中,大面积的低温区域处于出口中心的矩形区域,占据整个出口的2/3。其次是30°倾角三角凸结构,出口端的最低温度约为361 K,低温区域占整个出口的1/3。45°倾角三角凸结构的出口中心空气温度最高,达到403 K,空气射流在第6 排三角凸起就已经不再明显可见,出口端面上无明显的高温和低温分界线。原因是这3 种结构中,45°倾角三角凸结构不仅换热面积最大,而且中心通道最窄,强化换热效率最高。
图11 为3 种三角凸结构换热器通道中截面的速度分布云。

图11 三角凸结构换热器通道中截面的速度分布云Fig 11 Velocity distribution in the channel of three triangular heat exchanger
由图11可知,15°倾角三角结构的出口速度最小,为13.6 m/s;其次是30°倾角三角结构,速度为19.4 m/s;而45°倾角三角结构的最大速度达到33.8 m/s,远大于前二者,而且在近壁面附近也能观察到明显的涡旋结构。该结果与球凸结构的模拟结果十分近似,即同排凸起之间的距离越近,空间流体因为受到较强的流动冲击,而使湍流动能增大;而相邻两三角凸起之间的空间区域较大,流体的流动分离和再混合过程也有增大湍流动能的效果。
综上分析,45°倾角的三角凸在提高传热效率和减小流动阻力方面较其他2种三角凸结构都有着较好的表现。
2.4 球凸-三角混合结构换热器性能
将球凸与三角结构混合在一起进行分析,即凸起的前半段为1/4的圆球形球凸,后半段为45°倾角的三角凸,其结构如图12 所示,整个凸起宽度5 mm,高度2.5 mm,相邻凸起部分中心距离15 mm。
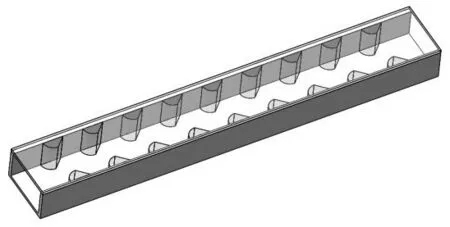
图12 球凸-三角混合结构换热器Fig 12 Spherical convex triangular hybrid heat exchanger
图13 为球凸-三角混合结构换热器的温度分布云。

图13 球凸-三角混合结构换热器的温度分布云Fig 13 Temperature distribution of spherical convex triangular hybrid heat exchanger
由图13 可知,出口端面处的低温区域为椭圆形状,最低温度约350 K。
球凸-三角混合结构换热器通道中截面的速度分布云见图14。

图14 球凸-三角混合结构换热器通道中截面速度分布云Fig 14 Cross section velocity distribution in channel of spherical convex triangular hybrid heat exchanger
由图14 可知,出口端最大速度为20 m/s,相邻两凸起之间的区域可观察到不明显的涡旋结构。
2.5 综合性能比较
换热器的进出口温度差和速度变化分别可以直观的表征其传热和阻力性能,而综合评价指标PEC则用来评估换热器的综合特性[11]。其表达式为:
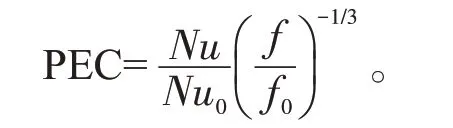
式中,Nu为换热器的努塞尔数,Nu0为无凸起光管的努塞尔数;f和f0分别为换热器和无凸起光管的阻力系数。
以上9种结构换热器的努塞尔数、阻力系数与PEC分别列入表1中。
由表1可知,PEC从大到小的排列依次是:纵向椭圆形球凸,45°倾角三角结构,交错布置肋片结构,同排布置肋片结构,圆球形球凸结构,球凸-三角混合结构,30°倾角三角结构,15°倾角三角结构和横向椭圆形球凸结构。这一排列顺序与凸起高度从大到小的排列顺序是一致的。

表1 不同模型的进出口温度差、阻力系数和PECTab 1 Inlet and outlet temperature difference,resistance coefficient and PEC of different models
对这一现象的解释如下:不同结构下,凸起部分使得通道收缩,流体流经该区域时速度增大,静压力下降;经过凸起之后通道扩张,流体速度减小,静压力上升,并通过速度的改变发生流体分离和再混合,并产生涡旋结构,冲击近壁面的流体边界层,提高综合性能。凸起的高度越大,其综合性能就越强。
3 结 论
以数值模拟的方式,研究了9种不同结构对换热器通道内空气的流动和换热性能的影响。主要结论如下:
1)肋片同排布置和交错布置2种结构对于提高传热效率和改进流动的效果几乎一致。
2)纵向椭圆形球凸的强化换热效果最好,其次是圆球形球凸,横向椭圆形球凸的效果最差。通道中的空气在纵向椭圆形球凸的出口中心速度最大,并且能观察到明显的涡旋结构;而横向椭圆形结构的出口中心速度最小。
3)对不同三角凸换热器的模拟结果显示,进出口温差和出口流体速度从大到小的排列完全一致:45°倾角大于30°倾角大于15°倾角三角凸结构。
4)9种结构的综合评价指标PEC从大到小的排列依次是:纵向椭圆形球凸,45°倾角三角结构,交错布置肋片结构,同排布置肋片结构,圆球形球凸结构,球凸-三角混合结构,30°倾角三角结构,15°倾角三角结构和横向椭圆形球凸结构。这一排列顺序与凸起高度从大到小的排列顺序是一致的。
研究结果可对选择和优化换热器结构提供理论依据。

