B-C五轴加工中心拓扑结构运动轴误差传递链建模

张银虎， 杨庆东， 王增新

（1. 北京信息科技大学 机电工程学院,北京 100192; 2. 超同步股份有限公司，北京 101500）

0 引言

五轴加工中心在复杂曲面加工领域占据着不可或缺的地位。而复杂曲面的加工精度和五轴加工中心的众多精度指标相关（几何精度、定位精度等），而每个精度指标对五轴加工中心的性能影响又有很大的不同。五轴加工中心的每个运动轴在装配的过程中会产生大量误差，使得加工轨迹和理想轨迹不能完美契合，导致五轴加工中心的加工精度受到一定的影响。

要实现对误差的有效补偿，最首要的便是构建更为精确的误差模型。从该层面来看，构建能够对五轴机床空间在几何层面上所存在误差进行精确分析的模型是很关键的，针对该建模过程开展相关探究是很有必要的。

目前相关研究者针对该领域开展的探究有：Kiridena 等[1]以D-H 法为基础构建了TTTRR 等不同形式的模型，并通过这些模型对在定位及体积方面所出现误差之间存在的映射关系进行了分析，该项探究的开展，促使D-H 法得到了更多关注，且在其他相关领域的建模中得到了较多运用；FAN 等[2]以多体系统理论为基础，针对多轴机床所存在几何误差构建模型的相关问题开展了全面探究。本文则主要提出了能够基于任意拓扑结构实现针对五轴加工中心运动轴所对应误差传递链设立相关模型的一种方法。基于该方法，不仅能够对各种结构类型的五轴加工中心运动轴所对应的误差传递链实现准确的获取，且能够利用计算机以更加简便的方式完成自动化建模及编程工作。

1 多体系统理论

该理论可以基于抽象层面对比较常见的各类机械结构做出全面分析，在针对机械系统开展分析方面能够发挥较好的效用。拓扑结构指针对机械系统内包含的较为关键的单元做出抽象处理以形成相应的抽象单元，然后根据各单元间原本存在的关联对这些抽象单元进行连接，继而得到相应的简化模型[3]。低序体阵列是对所构建拓扑结构进行描述时运用较多的一种，对于多体系统，设其所对应的惯性参考系M为A0体，在系统所包含的单元中任意选择一个并将其设定为A1体，然后沿与A1之间距离不断扩大的方向，由小到大针对各分值编制对应的序号。具体情况如图1所示，能够通过低序体阵列多图中所示的拓扑结构做出一定描述。若将R设定成该结构所包含的一个典型体，C是与其紧邻的低序体，则

能够对图1所示系统对应的低序体阵列进行推导，具体如表1所示。

表1 低序体阵列图

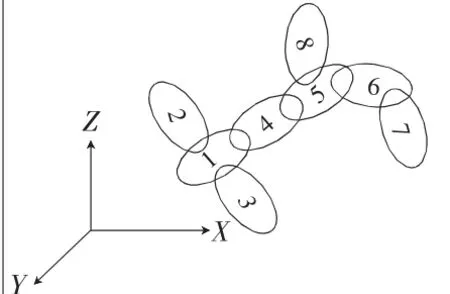
图1 多体系统拓扑结构图

2 五轴加工中心运动轴误差传递链建模

想要对五轴加工中心运动轴所对应的误差传递链进行有效获取，便是以多体理论为基础完成对其对应拓扑结构的构建。根据其所对应的低序体阵列，对其所对应的误差传递链做出推导。

2.1 五轴加工中心拓扑结构建模

对于五轴加工中心，在构建其拓扑结构时的主要依据为其所包含的支承件。将支承件Zn以矩形方框的形式进行体现；将不同支承件之间存在的连接关系Em以连线的方式进行体现。将连接关系分为固定Ejk及相对运动Eui两部分。基于上述内容能够得出拓扑结构所包含的信息集合

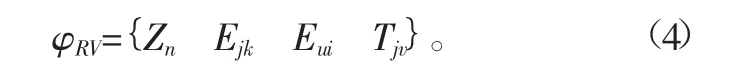
式中：n为支承件数目；k为机床固定连接数目；i为运动轴数目；v为相交节点数。

也就是，在获取拓扑结构所对应的集合φRV后，便能得到其所包含的所有信息，进而确定整个拓扑结构。以此能够针对具备结构类型不同的五轴加工中心设立相应的拓扑结构，具体如图2 所示。

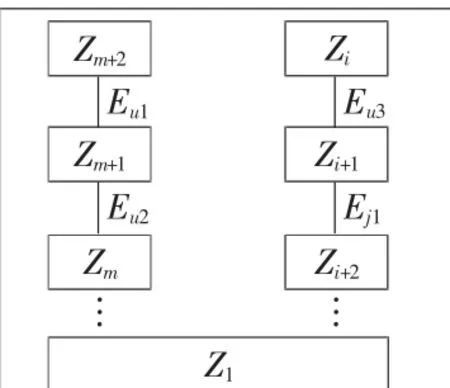
图2 五轴加工中心的拓扑结构图

五轴加工中心整体结构中，床身发挥着对其他部件进行支撑的关键作用，也是跟地面实现连接的重要部位。因此通过低序体阵列对整体拓扑结构进行描述的过程中，可以将工件所对应的坐标系设定为整体的惯性参考系，也就是说，在整个低序体中，床身所对应的序列号是0，结合上文对低序体算子做出的定义，能够对整个低序体阵列做出推导。以下便将某种类型的机床作为案例开展相关分析，其拓扑结构如图3 所示。得到其低序体阵列如表2所示。

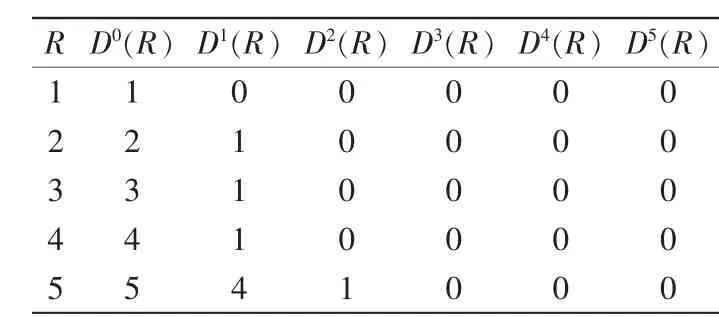
表2 某五轴加工中心的低序体阵列表

2.2 确认相对运动及连接矩阵

当运动轴数量为i，连接矩阵为V，将其阶数设定为i×2。其行顺序指机身至刀具点存在的所有运动轴排布的具体顺序。具体如图3所示，基于此能得出不同运动轴所连接的具体支承件的相关情况，具体如表3所示。

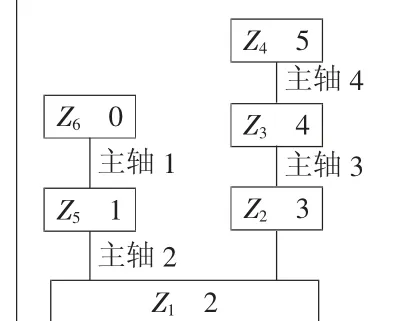
图3 某五轴加工中心结构拓扑结构图

表3 运动轴连接支承件表

说明：括号指支承件序列号。

从而得到该五轴加工中心运动轴支承件连接矩阵为

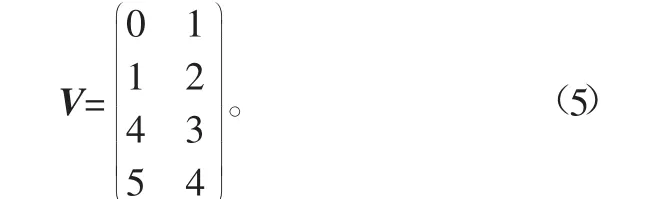
同一运动轴连接的支承件，所发生的运动永远具有相对性，即二者分别为运动件、静止件。设定支承件运动矩阵ϕ 的阶数为i×2，与相对运动矩阵E中矩阵行顺序一样。E（i，n）跟V（i，n）所涉及的支撑件是同一个。如果把V（i，n）设定成运动件，则E（i，n）=1，若将V（i，n）设定为支撑件，则E（i，n）=0，n=1，2。根据图3所示数据完成对表4的推导。

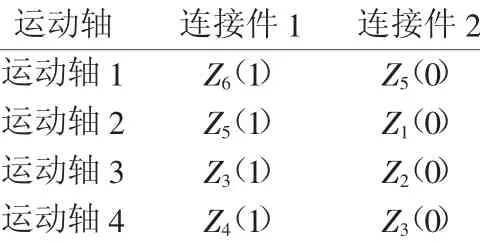
表4 运动轴与连接件相对运动表

从而可以得到该五轴加工中心运动轴连接件相对运动矩阵

2.3 五轴加工中心运动轴误差传递链获取

在获取五轴加工中心运动轴误差传递链前，最首要的便是以拓扑结构为基础推导出连接矩阵V及相对矩阵E。根据第2.1节内阐述的内容，能够完成该推导过程。

设定误差传动链坐标系中：指令位置项Ds，s指X、Y、Z、A、B、C等轴；自身定位误差ω；由于相对运动引发的误差ωhlsp2，如ω12指1、2轴对应坐标系由于出现相对运动引发的误差，且方向为1到2，ω21的方向为2到1，由于运动是可逆的，因此ω12=-ω21。

根据第2.2节所阐述的方式，以得到的拓扑结构图为基础，推导出工件所对应坐标系到刀具点所对应坐标系之间存在的各个运动轴的排布情况。

对于第i个运动轴，如果

根据上面提及的方法，完成所有运动轴在对误差进行传递时具体顺序的确定。然后将相互运动误差ωhlsp2加入其中，如在第i-1及第i个轴间增加误差ωi-1，i或-ωi，i-1。

3 五轴加工中心运动轴空间几何误差传递链建模

3.1 微分变换的五轴加工中心空间几何误差建模

针对五轴加工中心所存在几何误差构建相应模型的过程中，应通过微分运动替代运动轴所存在的几何误差发挥相关效用，如以微分变换为基础对不同运动轴所发生微分运动导致机床在开展理想化变换方面形成的误差进行阐释，进而形成以微分变换为基础设立几何误差所对应模型的相关方法。

随意选择一个五轴加工中心，并将其所包含运动轴的数量设定为i个，若其存在一定的几何误差，则对其进行变换处理的具体过程如图4所示，其中实线所体现的是不存在任何误差情况的理想变换，虚线体现的则是存在一定误差情况的实际变换。

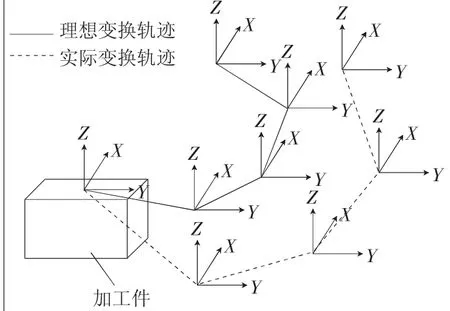
图4 实际变换轨迹图

将i-1Si定义成第i个轴在发生理想变换的过程中对应的矩阵，i-1Si体现的是第i个轴所对应坐标系的原点Oi与第i个轴所对应坐标系的原点Oi－1之间实现理想转换过程中所对应的矩阵。则

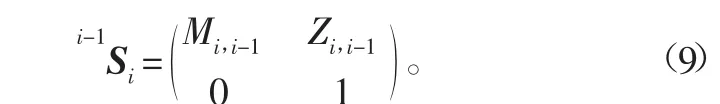
为对所设立模型进行简化，并尽可能减少整体计算规模，做出如下设定：第1个轴所处位置是工件所对应坐标系的原点，且与刀具对应坐标系的原点是相互重合的。则上述两个坐标系进行理想变换时对应的矩阵是

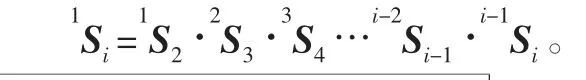
若设定第j个轴是存在一定几何误差的，且与其相对应的微分矢量为（ηjxηjyηjzωjxωjyωjz），则能够推导出微分变换算子j-1Δj：

对式（14）、式（15）进行整合，能够得出由于运动轴有着一定的误差而导致刀具所对应坐标系在位置上出现误差所对应的变换矩阵为：

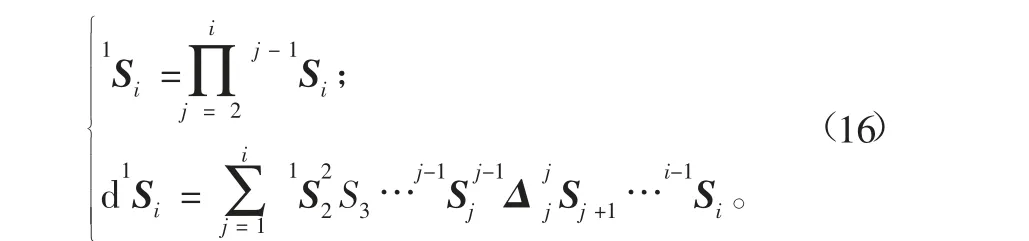
根据式（12），能够推导出d1Si的阶数为4×4，且第4列中列示的是对位置层面所存在误差进行体现的矢量。基于此，能够对刀具点在位置层面存在的一阶误差dZ进行计算：

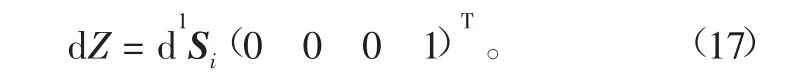
3.2 五轴加工中心运动轴误差传递链建模

将传递过程涉及各项的数量设定为m，根据得出的传递链能够推导出详尽的传递表，通过式（16）便能完成对相关模型的构建。该机床所对应的微分变换矩阵d1Sm、一阶位置误差dZ分别为

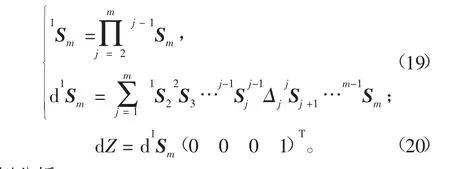
4 案例分析

为对所提出算法具备的适用性、普遍性进行有效验证，以五轴加工中心作为案例，其对应的拓扑结构图具体如图5所示。

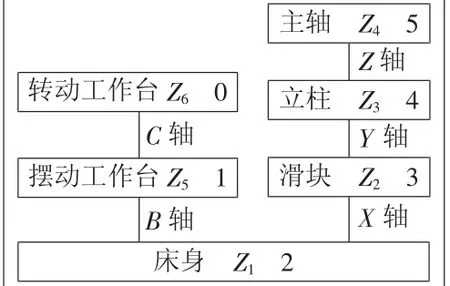
图5 B-C五轴加工中心拓扑结构图

根据五轴加工中心所对应的低序体阵列，能够推导出其所包含运动轴对各个支承件进行连接的情况，具

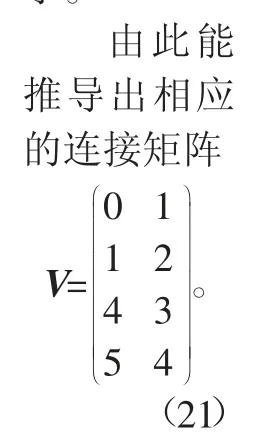
表5 B-C五轴加工中心运动轴连接支承件表 体如表5 所示。

根据拓扑图，能够对各支承件发生相对运动的具体情况进行推导，具体列示在表6中。

表6 B-C五轴加工中心运动轴连接支承件表

则B-C五轴加工中心运动轴连接件相对运动矩阵为

所以Z轴的误差传递为DY→ωY。

将相邻轴在发生相对运动出现的误差加入其中。本次所研究机床包含的运动轴数量为5个，形成的该类误差的数量为4个：ωCB，ωBX，ωXY，ωYZ。推导出相应的误差传递链：

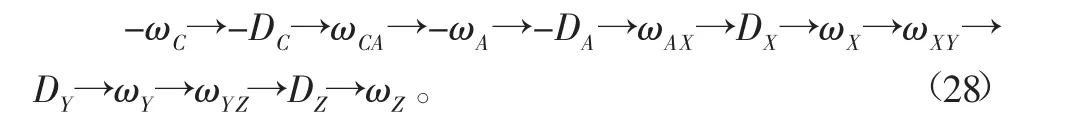
基于上述传递链能够推导出误差由B-C五轴加工中心传递至刀具点的具体情况，如表7所示。

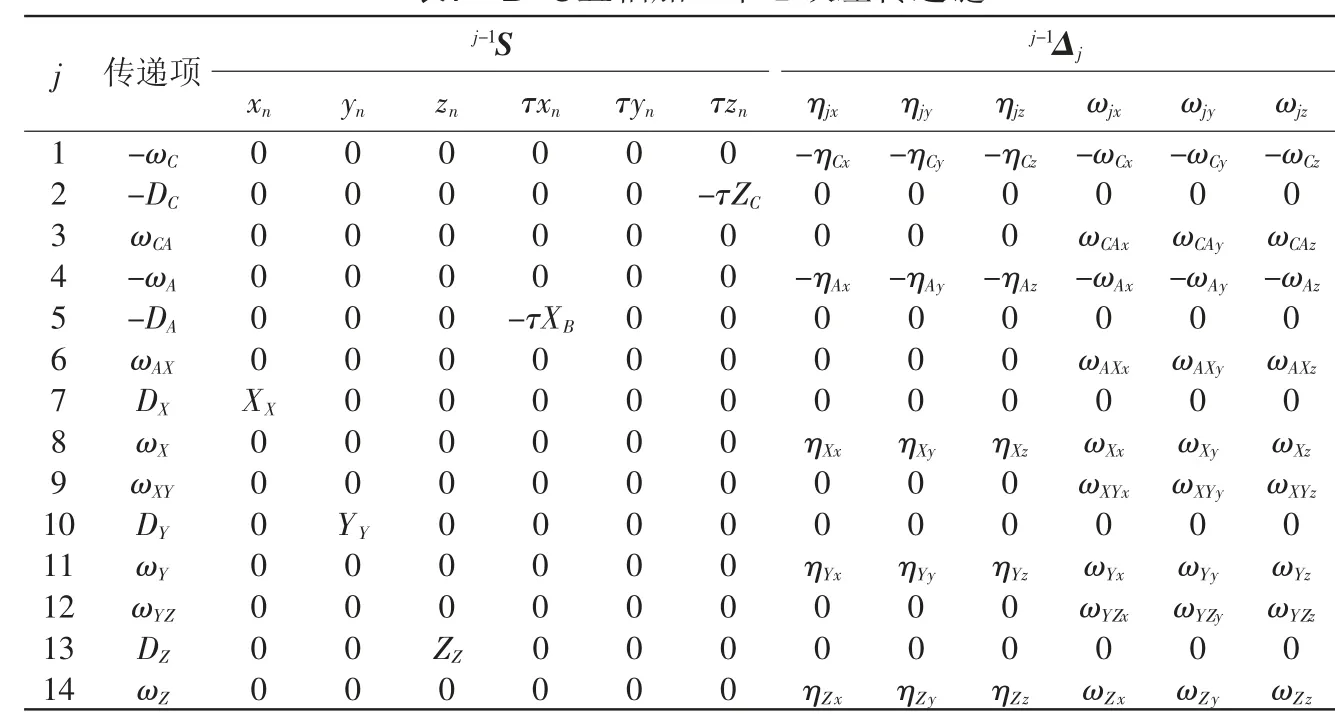
表7 B-C五轴加工中心误差传递链

根据第3节内提及的方法，对本次所探究B-C五轴加工中心中，实际刀具点所对应坐标系相对于工件所对应坐标系存在一阶空间位置误差d1Sm。

5 结论

1）本次探究的主要内容为：针对结构为任何类型的五轴加工中心，提出以其所对应拓扑结构为基础，推导出其所包含运动轴对应的误差传递链对应的模型、进行构建的方法及对应的数学模型。基于宏观层面得出误差在工件及刀具所对应坐标系间进行传递时二者间的关系，从理论层面上为计算空间误差奠定了一定基础。

2）以运动轴所对应的误差传递链及微分变换为基础，创建了五轴加工中心空间几何误差相关模型。并对误差传递链进行了详细阐述。将其与构建五轴加工中心空间几何误差模型联系起来。以五轴加工中心所对应拓扑结构为基础，推导出误差的传递过程。

3）以B-C五轴加工中心为案例开展相关分析，对本次所提出五轴加工中心空间误差几何建模方法的有效性、普遍性进行了实际验证。

4）后续探究中，会以本次提出方法为基础，探究公差分配的相关问题。