基于EEMD-PCA-LSTM滚动轴承故障识别与分类方法的研究

杨淑洁，周杨

（浙江海洋大学 海洋工程装备学院，浙江 舟山 316022）

0 引言

轴承是旋转机械的重要组成部分之一[1]，它的性能好坏直接能影响到与之相连接的机器设备的运行状况。一旦轴承发生故障，轻则导致机器停机，重则导致人员伤亡，这势必会给企业的安全生产和经济收入带来影响。所以，轴承故障的诊断成为了国内外研究的热点领域之一。

滚动轴承是一种标准件，其基本结构由内圈、外圈、滚动体、保持架4个部分组成，这4个部分是易发生故障的地方。当滚动轴承出现故障时，会产生异常的振动信号。因此，可以将振动信号作为轴承故障诊断的特征信号[2]。

轴承故障诊断主要围绕着故障特征提取和分类的问题进行研究。文献[3]提出了经验模式分解(Empirical Mode Decomposition, EMD)，这是一种新型自适应信号的时频处理方法，特别适用于非线性非平稳信号的分析处理。文献[4]针对EMD方法存在模态混叠的问题，采用噪声辅助分析，提出了集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)，能够有效抑制模态混叠的问题。

传统滚动轴承故障诊断通过时域或频域分析进行故障分类是比较困难的[5]，近几年随着机器学习和人工智能的发展，越来越多的学者将机器学习当中的算法引入到机械的故障诊断当中。文献[6]提出了一种改进的卷积神经网络(Convolutional Neural Network, CNN)与支持向量机(Support Vector Machine, SVM)相结合的方法，实验结果表明该方法在针对电动机轴承微小故障的智能识别具有很高的准确性。文献[7]提出了一种基于长短时记忆网络(Long Short-Term Memory Networks, LSTM)与迁移学习(Transfer Learning, TL)相结合的方法，实现了基于声发射技术对滚动轴承的智能分类。文献[8]提出了一种基于随机搜索与长短时记忆神经网络的滚动轴承故障状态识别算法，通过LSTM模型实现了从原始数据出发对轴承的故障数据信号进行特征提取和学习，无需人工干预，进而可以对轴承故障的分类。文献[9]提出了一种基于BP(Back Propagation, BP)神经网络滚动轴承故障诊断的多尺度局部特征学习方法，相对于传统的人为选择故障特征而言，此智能故障诊断技术能够更好地利用原始数据，自适应地从原始数据中学习故障特征，从而提高了故障诊断的准确性。

针对滚动轴承在发生故障时，目标振动信号的不稳定性和非线性导致故障特征难以提取，并且轴承的故障振动信号是属于时间序列数据且包含多种故障情况，为了提高故障分类问题的准确性，本文提出了一种基于EEMD与LSTM神经网络相结合的滚动轴承故障识别的方法。将轴承的振动信号经EEMD处理，得到了若干个本征模态函数(Intrinsic Mode Function, IMF)分量。为了剔除IMF分量当中的虚假分量，选出其中最能反映振动信号特征的分量，利用主成分分析法（Principal Component Analysis, PCA）对IMF分量进行降维。然后在计算降维后的分量占各自总能量的比例，把能量比所组成的特征向量作为LSTM神经网络的输入参数进行故障识别，将识别结果与EMD-BP、EEMD-KNN不同的故障分类模型所得的结果进行对比，结果表明，本文所用的方法对轴承故障识别的准确率更高。

1 故障识别的基础理论

1.1 EEMD算法

EEMD是基于EMD改进而来，在原有信号基础之上加入白噪声，利用白噪声频谱均匀分布的特点有效解决了EMD所出现的模态混叠现象。EEMD算法分解目标振动信号的步骤如下[10]：

1）确定EEMD的运算次数r和高斯白噪声的标准差σ。

2）在原始信息x(t)的基础之上，加入白噪声hi(t)，得到了新的信息xi(t)，其中i=1,2,3…,r，代表第i次分解：

1.2 PCA算法

目标振动信号经EEMD分解之后得到若干个IMF分量，在这些分量中，会存在一些虚假分量，它们的存在会影响后续LSTM神经网络分类的准确性。因此，为了去除这些虚假分量，选出其中最能反映目标振动信号特征的分量，需要对各分量进行降维。

PCA是一种无监督学习，属于数据降维的一种重要方法。通过PCA算法可以将原始数据从一个高维空间映射到低维度空间，其本质就是把原有的多个指标转化成几个代表性好的综合指标，这几个指标能够反映原来指标大部分的信息，并且各个指标之间保持独立。

利用PCA算法对EEMD分解后得到的j个IMF分量进行降维的过程如下[11]：

1）假设每组IMF分量中有j个IMF分量，每个分量有p个变量，则样本矩阵X如下：

4）计算标准化后的矩阵的相关系数矩阵和特征值λk，将其特征值从大到小排序。

5）根据主成分的累计贡献率φ大于85%的原则，计算前q(q＜j)个主成分累计贡献率φ，从而起到了降维的作用。

1.3 提取能量特征

不同故障状态下，轴承振动信号的能量分布是不同的，因此，利用这一特点计算IMF主成分分量的能量占总能量的比例，将其作为LSTM神经网络故障识别的输入参数。提取能量特征的步骤如下[12]：

1）目标振动信号经EEMD分解和PCA降维之后，得到了q个IMF主成分分量，计算各分量的能量

1.4 LSTM神经网络

LSTM是在循环神经网络（Recurrent Neural Network,RNN）的基础之上改进而来，是一种RNN特殊的类型。通过增加遗忘门、输入门及输出门的结构来选择性地决定信息的保留和遗忘[13]，从而解决了RNN在较长时间序列训练过程中产生的梯度爆炸和梯度消失的问题。其中，遗忘门主要决定从细胞状态中遗忘什么信息，输入门决定向细胞状态更新信息，输出门决定向细胞状态中更新信息[14]。LSTM的单元结构示意图如图1所示，计算过程的公式如下：

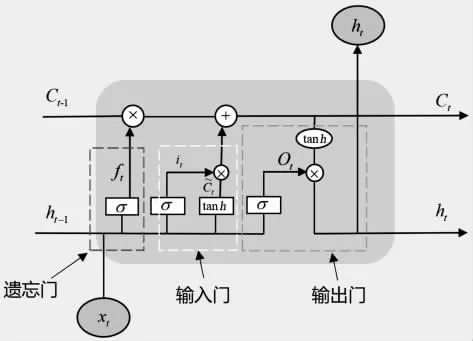
图1 LSTM单元结构示意图

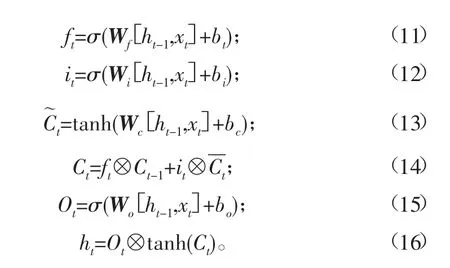
2故障识别流程设计

针对滚动轴承在发生故障时，故障振动信号的不稳定性和非线性导致故障特征难以提取并且轴承的故障振动信号是属于时间序列数据且包含多种情况，为了提高故障分类问题的准确性的这一情况，提取了一种基于EEMD-PCA与LSTM 神经网络的滚动轴承故障识别的流程如图2所示，此方法的步骤如下：

图2 故障识别的流程图

1）分别采集不同工况状态下的滚动轴承的振动信号，利用EEMD算法对滚动轴承的振动信号进行分解，得到了若干个本征模态函数分量IMF。

2）在这些经分解后的若干个IMF分量中，会存在一些虚假分量，它们的存在会影响后续LSTM神经网络分类的准确性。为了去除虚假分量，提高LSTM神经网络的识别率，可以利用主成分分析法对这若干个IMF分量进行降维，选出其中最能反映目标振动信号的特征分量。

3）计算IMF主成分分量占各自总能量的比例，再将能量比作为LSTM神经网络的输入参数。

4）将数据集划分成训练集和测试集，用于LSTM神经网络模型的训练和测试。

5）将训练集作为LSTM神经网络的输入参数进行训练，最终得到了轴承的故障识别模型。然后再将测试集输入到已经训练好了的模型当中去，将其输出的结果与实际结果进行对比来判断模型的识别率。

3 实验分析

3.1 实验数据描述

为了验证本文所提出的EEMD-PCA与LSTM神经网络的有效性，本文利用轴承的故障数据对该算法进行了仿真验证。仿真采用的实验数据来自美国凯斯西储大学（Case Western Reserve University,CWRU）轴承数据中心[15]，该数据集被广泛用于轴承的故障诊断领域，所以，该数据被本领域所公认有效。如图3从左至右所示，实验器材有电动机、转矩传感器、编码器、测力计、测功器。被测轴承为6250-2RS JEM KSF，深沟球轴承，轴承直径为0.1778 mm。采样频率为12 kHz，主轴转速为1772 r/min。使用的是驱动端（DE）轴承故障数据，采用电火花技术进行加工以模拟其故障，故障直径为0.1778 mm。包括内圈、外圈、滚动体故障，其中外圈故障采用的是以负荷区6点钟方向为中心的3点钟方向的数据。每种故障共有12组数，每组取4100个数，8组训练组，4组测试组。

图3 实验器材图

3.2 故障特征提取及识别

图4所示分别为轴承在滚动体故障、内圈故障、外圈故障、正常4种情况下振动信号的时域图和频域图。

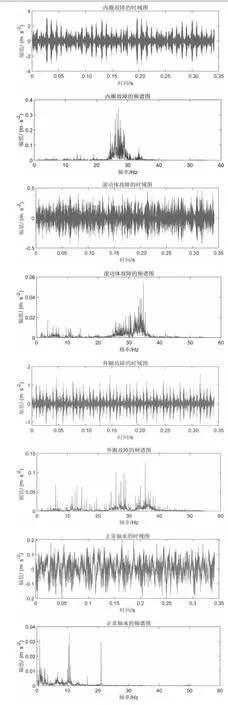
图4 轴承在不同情况下振动信号的时域和频域图

根据Huang等[3]推荐的标准可知，本文的高斯白噪声标准差选为0.2，平均运算次数选为100，利用EEMD算法对轴承外圈故障的振动信号进行处理，得到了如图5所示的IMF分量。

图5 轴承外圈故障信号EEMD分解图

从EEMD分解图可以看出，轴承外圈故障信号可以分解为13组IMF分量。在这些分量中存在一些虚假分量，它们的存在会影响后续LSTM神经网络分类的准确性。为了去除虚假分量，提高LSTM神经网络的识别率，可以利用主成分分析法对这若干个IMF分量进行降维，选出其中最能反映目标振动信号特征的分量。表1是轴承外圈故障信号的所有IMF分量的贡献率。

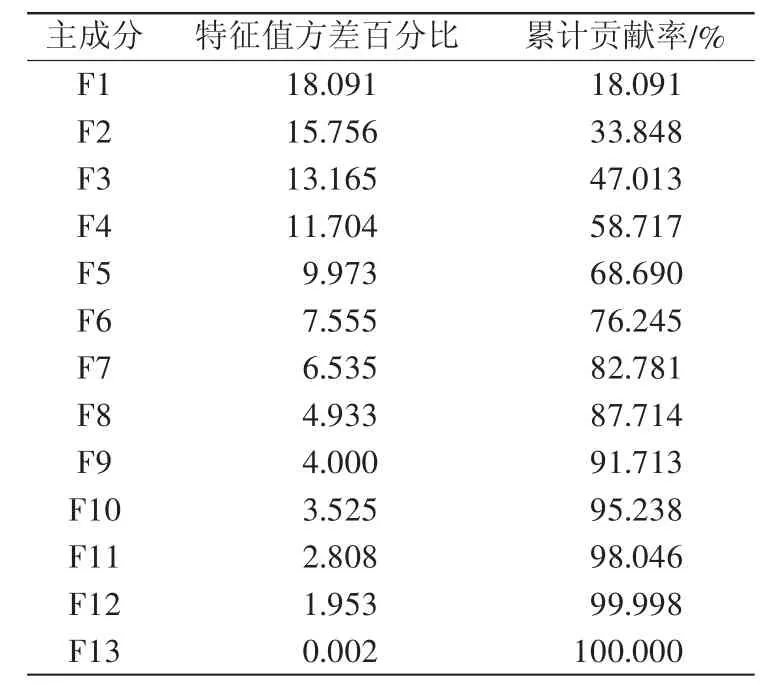
表1 轴承外圈故障信号的IMF分量的贡献率

根据PCA的选取原则可知，选取表1的前8个主成分。同理可得，分别对轴承在正常情况下、内圈故障、滚动体故障进行处理，各分量的累计贡献率如表2所示。

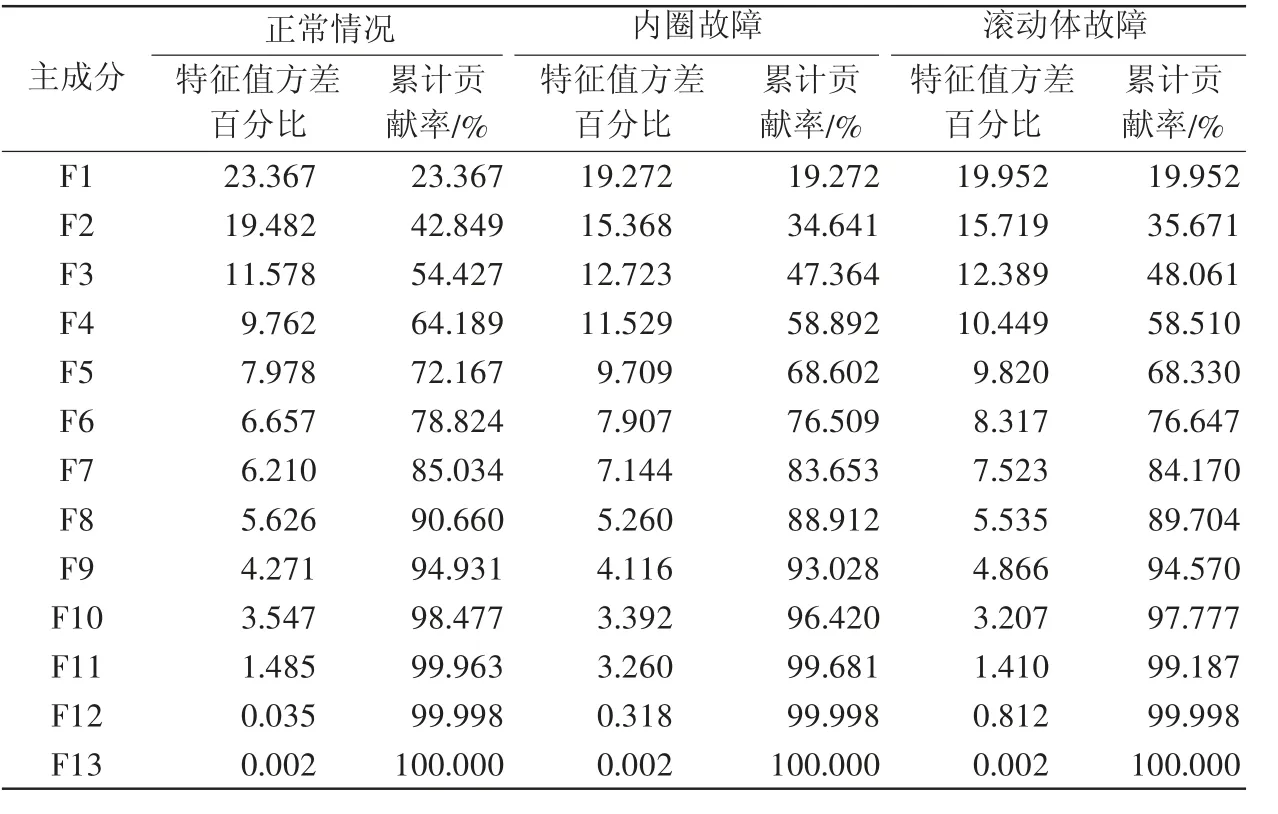
表2 轴承在不同工况下各主成分的贡献率

由表2可知，轴承在正常情况下、内圈故障下、滚动体故障下的IMF分量在经过主成分分析法处理后，前8组主成分的累计贡献率分别是90.660%、88.912%、89.704%，其值均大于85%。

利用式（8）和式（9）可以分别计算出轴承外圈的IFM主成分分量的能量比，如表3所示。

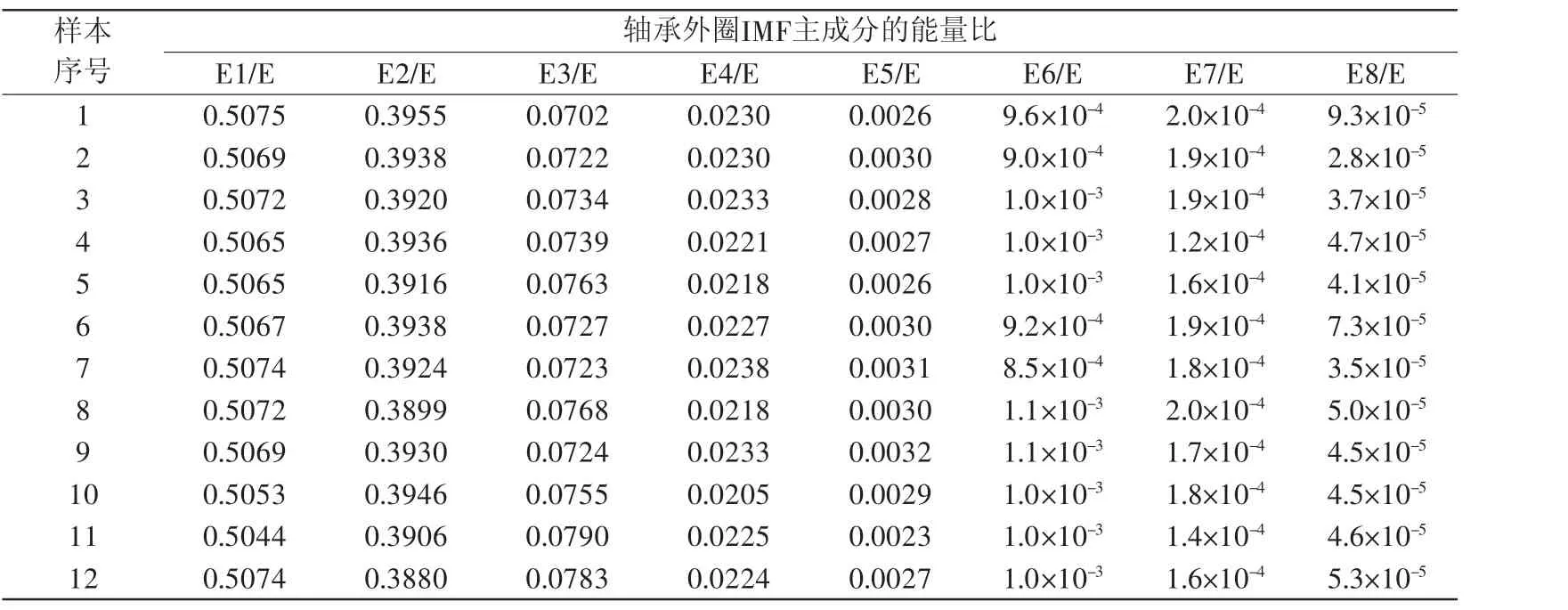
表3 轴承外圈IMF主成分分量的能量比

同理，可分别计算出轴承在正常情况下、内圈故障下、滚动体故障下IMF主成分分量的能量比，由于篇幅有限，此处仅给出3种情况下的4组样本的IMF主成分分量能量比，如表4所示。

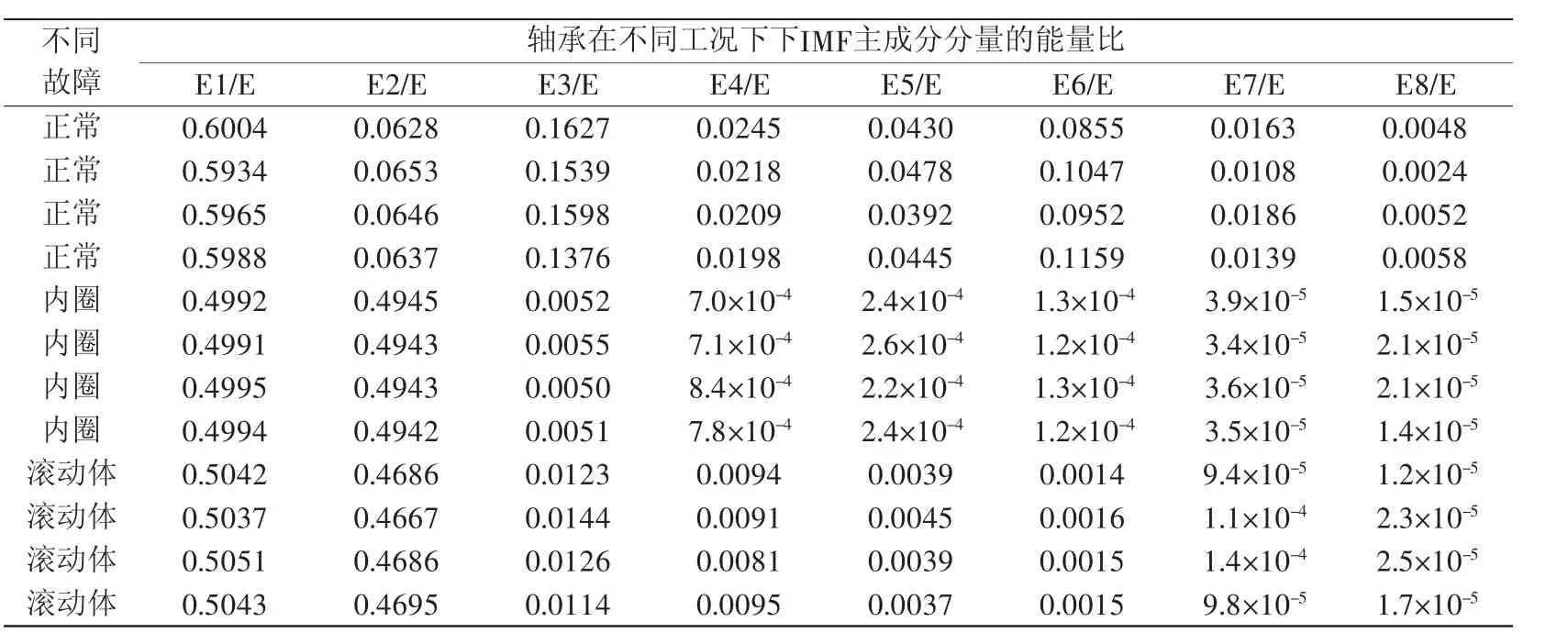
表4 轴承在不同工况下IMF主成分分量的能量比

再将训练集的IMF主成分分量的能量比作为特征向量输入到LSTM神经网络当中去进行训练。从轴承的每种工况下随机抽取8组作为训练样本，4组作为测试样本。为了更好地进行LSTM神经网络训练，需要对轴承在不同工况下的IMF主成分分量的能量比进行标签分类处理，处理结果如表5所示。

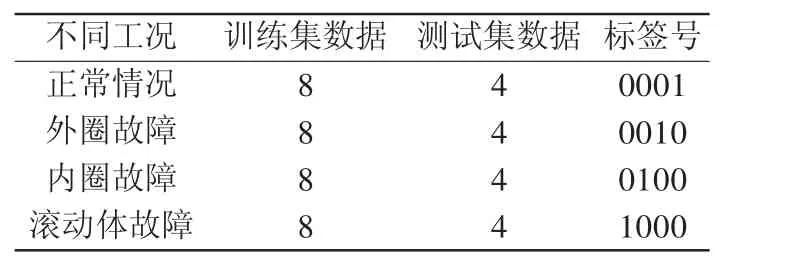
表5 轴承故障数据标签分类处理

LSTM神经网络测试的结果如表6所示，任取其中的一次训练过程如图6所示。

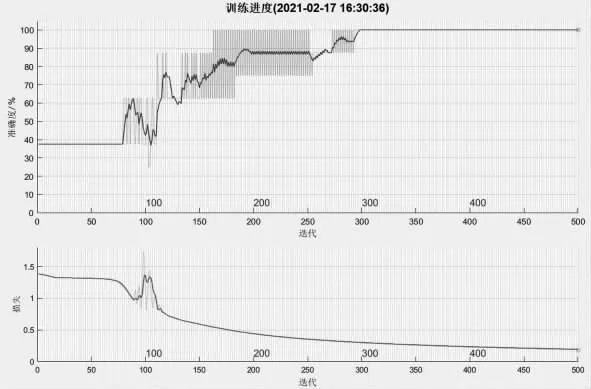
图6 LSTM神经网络训练进度图

表6 LSTM神经网络测试的结果

为了验证EEMD-PCA 与LSTM神经网络方法的有效性，在相同的数据下与EMDBP神经网络[16]、EEMD-KNN[17]进行对比，取其中的一次误差迭代曲线如图7所示。

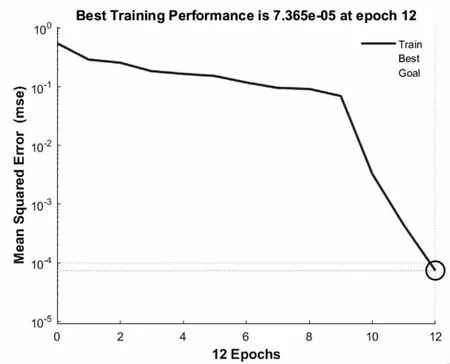
图7 误差迭代曲线

对比表7可知，在识别轴承故障状态时，本文的故障诊断模型分类正确率分别高于EMD-BP、EEMD-KNN故障诊断模型的分类正确率，由此可知，本文所采用的方法可以有效地进行轴承的故障识别。

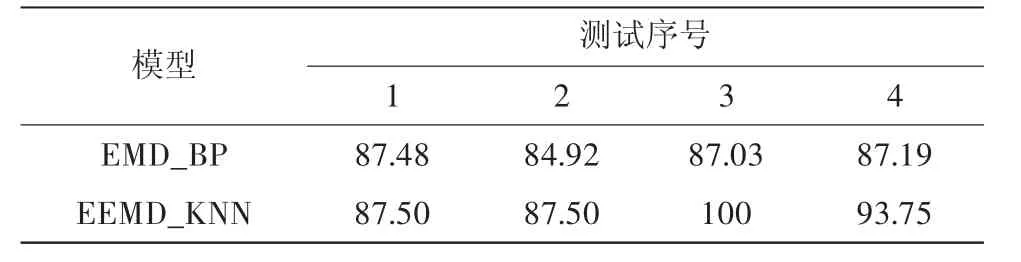
表7 不同模型下的分类正确率 %

4 结语

本文提出了一种基于EEMD-PCA与LSTM神经网络相结合的滚动轴承故障识别的方法，首先对轴承不同状态下的目标振动信号进行EEMD分解，得到了若干个IMF分量。在这些IMF分量中，会存在一些虚假分量，它们的存在会影响后续LSTM神经网络分类的准确性。为了去除这些虚假分量，选出其中最能反映目标振动信号特征的分量，可以利用PCA算法对各分量进行降维。然后再计算IMF主成分分量的能量占各自总能量的比例，将能量比所组成的特征向量作为LSTM神经网络故障识别的输入参数。最后将识别结果与EMD-BP、EEMD-KNN所得的结果进行对比，对比结果表明，本文所提出的方法在进行轴承的故障诊断上更具有优势，从而验证了该方法的有效性。