页岩油储层可压性分析及指数预测

吕照 ，刘叶轩 ，陈希 ，贾海正 ，李嘉成 ，梁利喜 ，丁乙

（1.中国石油新疆油田分公司工程技术研究院，新疆 克拉玛依 834000；2.西南石油大学油气藏地质及开发工程国家重点实验室，四川 成都 610500）

0 引言

全球石油工业目前正逐渐从常规油气向非常规油气转变。页岩油作为非常规油气的一种，其资源潜力巨大，被誉为世界能源的“黑金”[1]。与页岩气类似，页岩油的高效开采也需要水平井体积压裂技术[2-3]。为实现较好的压裂改造效果，必须先对页岩油储层开展可压性分析，制定相对应的压裂工艺措施，从而避免盲目压裂，提高压裂效率[4-5]。

可压性的评价最早基于岩石脆性特征，岩石脆性越强，可压性越好[6]。但随着研究的深入，学者们发现影响可压性的因素众多，仅根据岩石脆性并不能判断储层的可压性，岩石组构、岩石力学强度特征、地应力等因素均会对储层可压性产生影响。Yuan等[7-9]结合岩石脆性与断裂韧性，开展可压性评价，认为地层脆性越好、断裂韧性越低，可压性越强；赵金洲等[10-11]结合岩石抗压强度、抗剪强度、抗张强度及组构特征，分析了储层可压性；赖富强等[12]将储层地应力状态引入了可压性分析。此外，考虑储层可压性的各类影响因素，借助神经网络、灰色关联、层次分析等数理方法，众多学者建立了相应的可压性指数，用于指导现场压裂分段分簇设计[13-14]。

受到近年来页岩气火热开采的影响，现有可压性的理论方法均来源于页岩气压裂技术研究。然而，页岩气与页岩油具有差异性，尤其页岩气为典型的自生自储，但页岩油具有明显储、隔层特征。已有研究显示，储层内部压裂缝的扩展会受到隔层影响，但现有可压性研究均没有涉及隔层效应分析，这不利于指导页岩油储层压裂设计。因此，本文结合室内力学实验、数值模拟、图像处理及数理分析等方法，分析了隔层效应对页岩油储层可压性的影响机制，建立了适用于页岩油储层的可压性指数，为页岩油储层可压性评价提供了新的理论方法。

1 页岩油储层地质力学特征

本文研究对象为准噶尔盆地某页岩油储层，储层岩样矿物组成以石英与长石为主。目的层上下均存在高强度应力隔层（较厚且稳定的泥岩层），对裂缝纵向延伸产生遮挡。基于工区资料，地层压力主要分布在30.4～68.3 MPa，垂向地应力（σv）、最大水平地应力（σH）、最小水平地应力（σh）分别分布在 65.1～108.6，64.4～103.5，41.1～95.3 MPa。储、隔层的岩石力学参数通过室内三轴抗压强度与巴西劈裂实验获取，结果如表1所示。由表可见，储层与隔层的力学特征具有明显的差异性，隔层强度远大于储层。

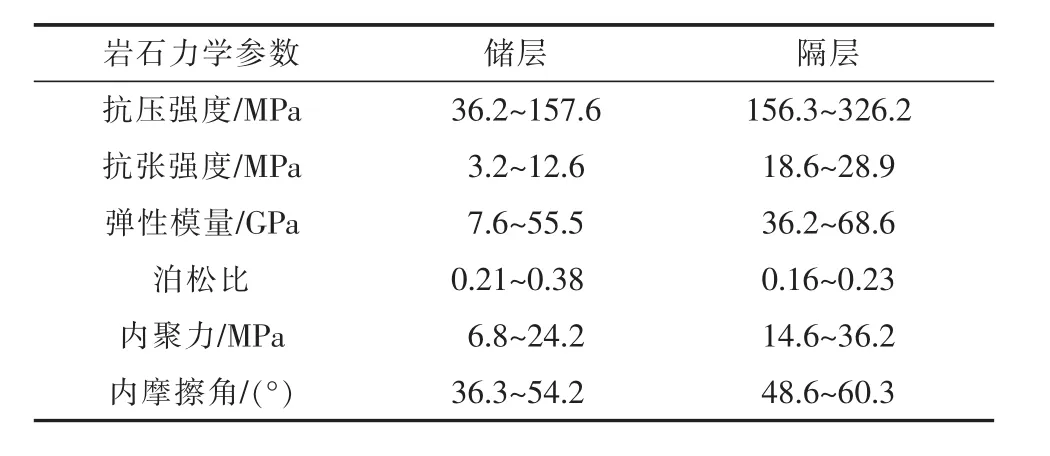
表1 储层与隔层的岩石力学参数

2 页岩油储层可压性分析数模方法

2.1 数值模型的理论基础

本次研究所用的数值模拟软件为RFPA2D。该软件是以弹性力学、损伤力学及Biot渗流理论为基本原理，考虑细观结构非均匀性及流固耦合作用的岩石破坏过程分析系统[15-16]。模型中假设流体在岩石介质中的流动遵循Biot渗流理论，满足Biot渗流-应力耦合方程[17-18]。当岩石单元的应力或者应变状态满足某个特定的损伤阈值时，单元开始出现损伤，可通过拉伸准则与摩尔-库伦准则对岩石损伤进行分析。模拟计算中首先进行拉伸准则判断，当拉伸破坏不满足时，再开展剪切破坏判断。

岩石单元拉伸损伤准则为

式中：σ3为岩石单元最小主应力，MPa；S为岩石单元抗拉强度，MPa。

岩石单元剪切损伤准则为

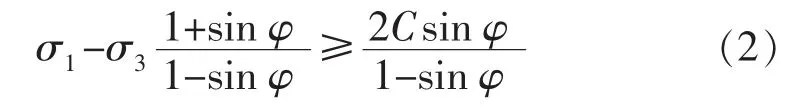
式中：σ1为岩石单元最大主应力，MPa；φ为岩石单元内摩擦角，（°）；C 为岩石单元内聚力，MPa。

2.2 数值模型构建与验证

基于上述数模理论，建立了储、隔层条件下的压裂数值模型（见图1）。图1b中，绿色区域为强度较大的隔层，蓝色区域为强度较小的储层。本模型主要针对储、隔层特征，忽略地层内部天然裂缝的影响。模型尺寸设计为井筒尺寸（直径为40 mm）的50倍，即2 m×2 m，网格划分为 360 000（600×600）个细观单元。

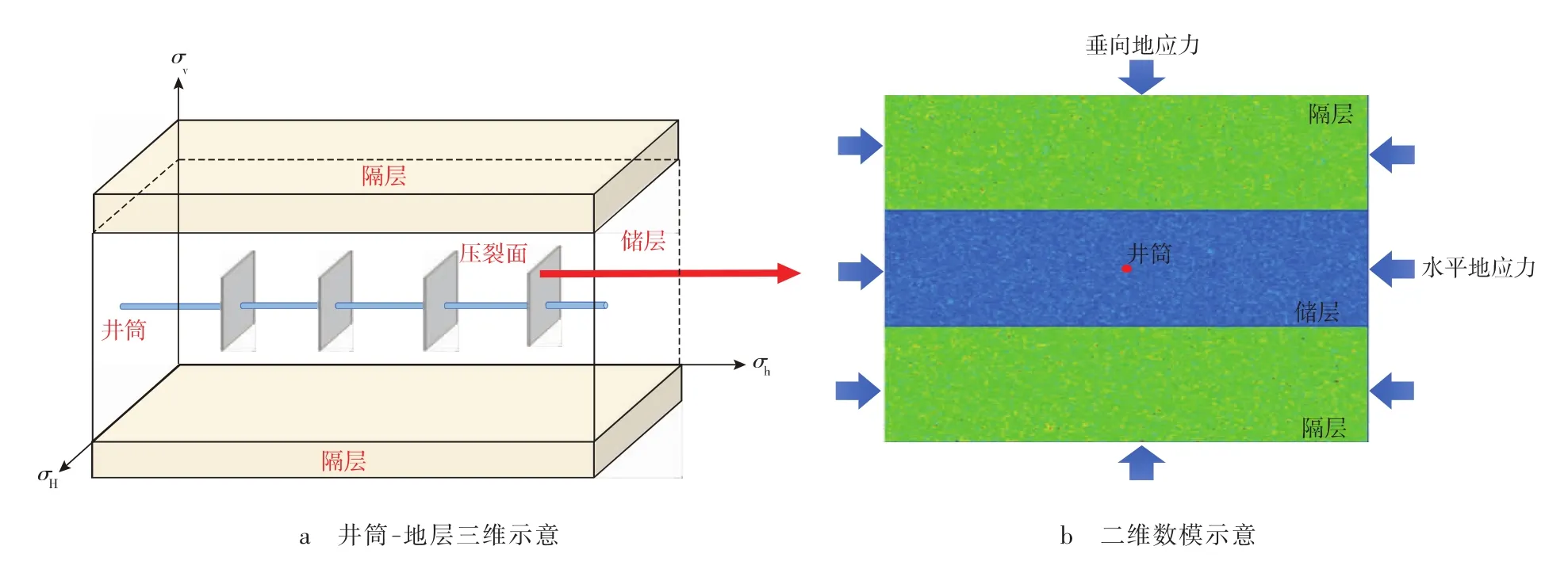
图1 储、隔层条件下的压裂数值模型

储层与隔层的岩石力学参数见表1。模型边界分别施加水平地应力与垂向地应力，井筒内采用渗流空洞载荷加载方式，逐步增加井筒内流体压力，单步增量为1 MPa。其中，地层压力、垂向地应力、最大水平地应力及最小水平地应力采用上述地质力学特征参数进行赋值。此外，地层基础物性参数取值为：孔隙度5.4%，渗透率 0.02 ×10-3μm2，密度 2.45 g/cm3。

采用现场7口井的破裂压力测试对本文数值模型进行验证。利用测井数据，计算得到压裂位置处的地应力、地层压力及岩石强度，从而对模型进行赋值。模拟过程中，取井壁开始破裂时的井筒流体压力为预测破裂压力，与实际压裂施工曲线上的破裂压力进行对比 （见图2）。

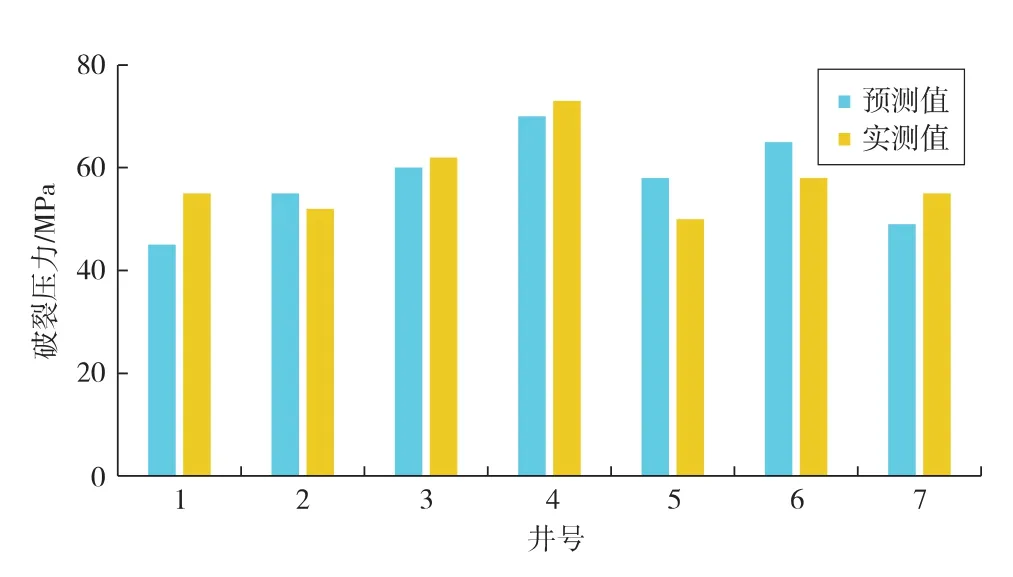
图2 数模预测与实测破裂压力值对比

由图2可见：破裂压力的实测值与数值模型的预测值吻合程度较好，两者差值均在10 MPa以内，证明了本文模型的准确性。

2.3 模拟结果处理

基于上述数值模型，逐步增加井筒压力，形成井周压裂缝扩展图（见图3a，图中黑色为压裂缝，彩色代表储层孔隙压力值，离裂缝越近，孔隙压力值越大）。在此基础上，采用灰度处理与二值化法[19]，获得了压裂缝扩展的二值化图（见图3b，3c）。二值化图中，黑色裂缝部分像素点值为1，白色（代表没压开）部分为0。基于统计分析，可以得到整个压裂缝延伸过程中的无因次面积A为

图3 压裂缝模拟结果及面积示意

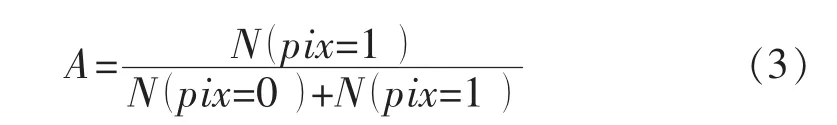
式中：N（pix=0）为像素点值为0的数量；N（pix=1）为像素点值为1的数量。

压裂缝无因次面积越大，代表储层越容易被压开，可压性越好。因此，可利用压裂缝无因次面积对页岩油储层可压性进行评价分析。

3 页岩油储层可压性影响因素

基于上述数值模拟，认为在同样的井筒压裂条件下，压裂缝无因次面积越大，储层可压性越好。因此，以数值模拟的第60步、70步及80步的压裂缝无因次面积为指标，开展页岩油储层可压性的影响因素分析。

3.1 储层力学特征

基于储、隔层压裂数值模型，分析不同储层力学参数下的可压性（见图4）。由图可见：当储层抗张强度与抗压强度降低时，压裂缝无因次面积增加，储层可压性增强。基于地层破裂压力的定义与计算理论，地层强度（尤其抗张强度）、地层破裂压力降低[20]，表示在相同工艺条件下，地层更易被压开，在数值模拟中可形成更大的压裂缝面积，储层可压性提高。此外，弹性模量增大、泊松比降低时，无因次面积呈现增大趋势。基于Rickman定义，高弹性模量与低泊松比代表更强的岩石脆性，导致可压性增强。综上所述，高脆性、低抗张强度的储层具有更好的可压性，与常规储层可压性分析相吻合，说明隔层效应对储层可压性的机制没有影响。

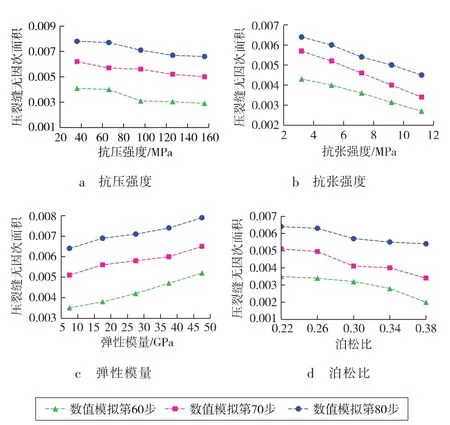
图4 储层力学参数对储层可压性的影响

3.2 隔层效应

设置恒定储层强度参数，分析隔层效应对储层可压性的影响（见图5）。当隔层抗张强度与抗压强度增加时，压裂过程中的压裂缝无因次面积逐渐减小，说明储层可压性降低，高强度隔层对储层压裂缝扩展具有抑制效果。这是由于在压裂过程中，井周裂缝扩展受到井周张应力与压应力的控制，更强的隔层抗张强度与抗压强度导致储、隔层整体强度增大，压裂缝不易向外延伸，从而对可压性具有抑制作用。

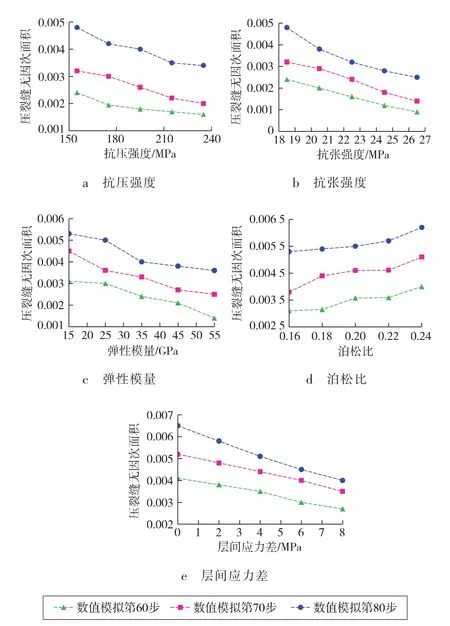
图5 隔层效应对储层可压性的影响

当隔层弹性模量增大、泊松比降低时，压裂过程中的无因次面积逐渐减小，说明储层可压性降低。隔层弹性越大，隔层岩石弹性阶段承压能力越强，越不易进入塑性及破坏阶段，对储层压裂缝扩展的屏蔽作用则更显著[21-22]。由此可见，当隔层弹性能力更强时，对储层的可压性减弱作用更明显。

随着层间应力差的增大，压裂缝无因次面积减小，储层可压性减弱[23-24]。较大的层间应力差易形成强应力遮挡现象。高地应力对隔层具有明显挤压作用，使得隔层强度增大，且更为致密，从而导致隔层对储层可压性的抑制作用增强[25-26]。

3.3 地应力

基于恒定的储、隔层条件，分析了不同地应力状态下的储层可压性（见图6）。其中，地应力为最大水平地应力，地应力差为垂向地应力与最大水平地应力的差值。分析结果显示：随着地应力、地应力差增大，压裂缝无因次面积减小，储层可压性减弱。主要原因在于，高地应力、高应力差条件下，储层压实效应显著，从而导致储层可压性受到限制。

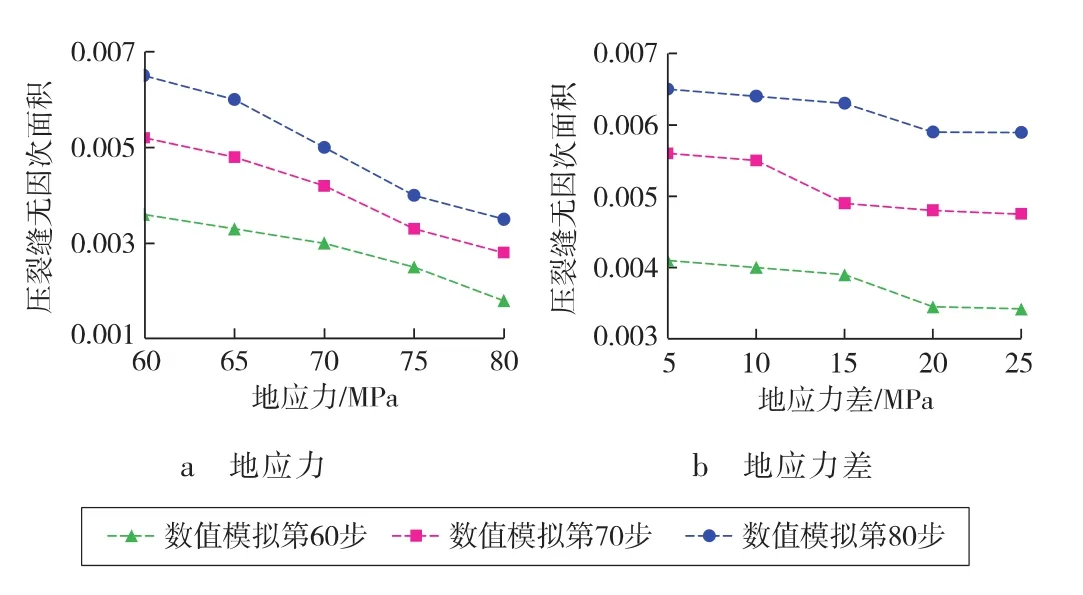
图6 地应力对储层可压性的影响

4 页岩油储层可压性指数构建

基于上述可压性分析，采用灰色关联法确定各类影响因素（储层力学特征、隔层效应及地应力）的重要性，进而通过层次分析法确定各影响因素的权重系数，建立可压性指数方程。根据灰色关联法原理，母序列为数值模拟第60步、70步及80步下的压裂缝无因次面积，子序列为数值模拟第60步、70步及80步下的储层抗压强度、储层抗张强度、储层弹性模量、储层泊松比、隔层抗压强度、隔层抗张强度、隔层弹性模量、隔层泊松比、层间应力差、地应力及地应力差。归一化后的母序列与子序列的差值绝对值Δi（k）为

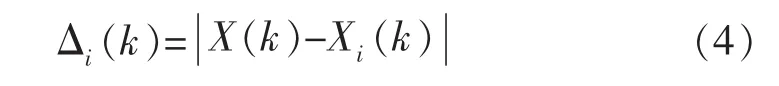
式中：i为子序列编号；k为母序列编号；X（k）为第k个母序列的归一化值；Xi（k）为第k个母序列下的第i个子序列的归一化值。

基于Δi（k），求取影响因素对压裂缝无因次面积的关联系数 ξi（k）：

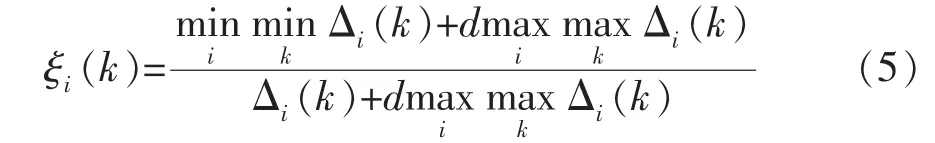
基于关联系数，得到关联度γi：

式中：n为参考点个数。

图7为各类影响因素与可压性的关联度，关联度越高，说明该因素对压裂缝无因次面积的影响越大。

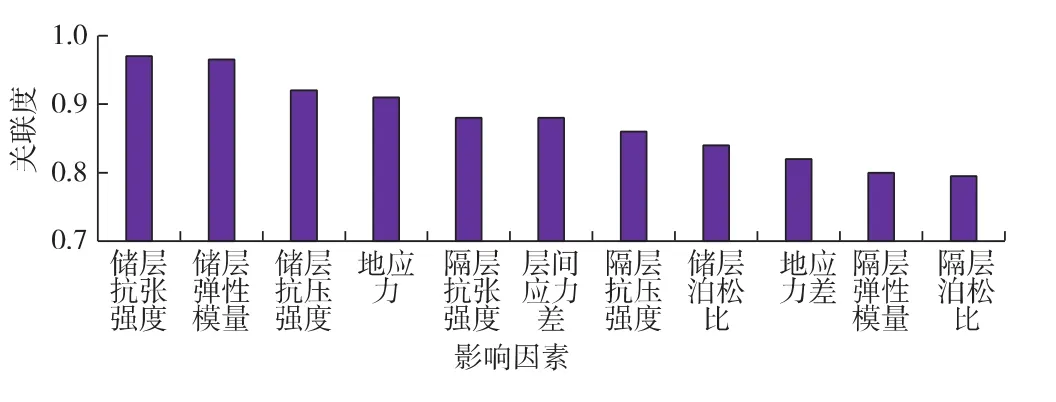
图7 各类影响因素与储层可压性的关联度

基于此，依据层次分析法，确定各类因素的重要程度矩阵，采用矩阵的最大特征根的特征向量求取权重系数分布，得到储层可压性指数Findex的预测方程为

式中：St为归一化的储层抗张强度；Er为归一化的储层弹性模量；σrc为归一化的储层抗压强度；σin为归一化的地应力；Sbt为归一化的隔层抗张强度；Δσd为归一化的层间应力差；σbc为归一化的隔层抗压强度；μr为归一化的储层泊松比；Δσh为归一化的地应力差；Eb为归一化的隔层弹性模量；μb为归一化的隔层泊松比。

5 实例应用分析

基于上述可压性指数预测方程，对准格尔盆地某页岩油储层X水平井开展可压性预测。根据工区资料，X井目标层位上部发育泥岩隔层。计算过程中，隔层地质力学参数固定，利用储层段上部（隔层）钻井、测井资料，取隔层段地质力学参数平均值，得到隔层段地质力学参数为：抗张强度24.4 MPa，抗压强度202.3 MPa，弹性模量52.4 GPa，泊松比 0.23，最小水平地应力75.0 MPa。储层地质力学参数通过储层水平段测井数据进行计算。通过隔层与储层的最小水平地应力差值，获取储层段各深度点的层间应力差。

结合工区隔层与储层地质力学特征，利用本文构建的可压性指数预测方法，求取水平段储层可压性指数分布（见图8a）。图中深度为斜深，分析井段为储层水平段。

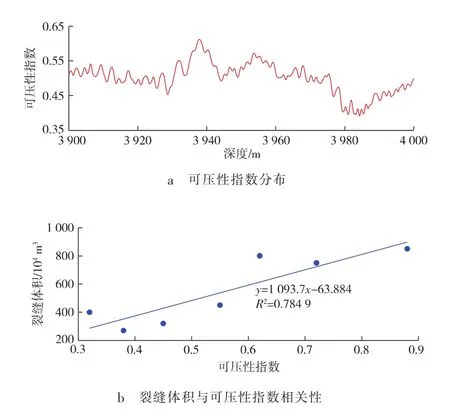
图8 储层可压性指数适用性验证

基于可压性的分布特征，结合该井的微地震监测结果，对比分析了微地震监测下的裂缝体积与可压性指数的相关性（见图8b）。裂缝体积与可压性指数具有较好的相关性（R2=0.784 9），证明了本文构建的页岩油储层可压性指数预测方法的准确性与适用性。

6 结论

1）基于RFPA2D数值模拟软件，构建了具有储、隔层的压裂缝扩展模型。在此基础上，借助二值化图像处理手段，构建压裂缝无因次面积，进而结合灰色关联法与层次分析法，形成了一种储、隔层条件下的储层可压性指数预测方法，并验证了其适用性。

2）隔层效应不改变储层可压性的影响机制，高脆性、低抗张强度储层具有更好的可压性，当隔层抗压强度增加时，储层可压性降低，高强度隔层对储层压裂缝扩展具有抑制作用。当隔层弹性模量增大、泊松比降低时，隔层与储层岩石的整体弹性增强，井周岩石承压能力增强，不易进入塑性及破坏阶段，从而对整体可压性具有弱化作用。

3）较大的层间压力差易形成强应力遮挡现象，导致隔层对储层可压性的抑制作用增强。随地应力、地应力差增大，整个储层压实效应增大，导致储层可压性受到限制。